Cross-Modal Hamming Hashing

Abstract

Cross-modal hashing enables similarity retrieval across different content modalities, such as searching relevant images in response to text queries. It provide with the advantages of computation efficiency and retrieval quality for multimedia retrieval. Hamming space retrieval enables efficient constant-time search that returns data items within a given Hamming radius to each query, by hash lookups instead of linear scan. However, Hamming space retrieval is ineffective in existing cross-modal hashing methods, subject to their weak capability of concentrating the relevant items to be within a small Hamming ball, while worse still, the Hamming distances between hash codes from different modalities are inevitably large due to the large heterogeneity across different modalities. This work presents Cross-Modal Hamming Hashing (CMHH), a novel deep cross-modal hashing approach that generates compact and highly concentrated hash codes to enable efficient and effective Hamming space retrieval. The main idea is to penalize significantly on similar cross-modal pairs with Hamming distance larger than the Hamming radius threshold, by designing a pairwise focal loss based on the exponential distribution. Extensive experiments demonstrate that CMHH can generate highly concentrated hash codes and achieve state-of-the-art cross-modal retrieval performance for both hash lookups and linear scan scenarios on three benchmark datasets, NUS-WIDE, MIRFlickr-25K, and IAPR TC-12.

1 Introduction

With the explosion of big data, large-scale and high-dimensional data has been widespread in search engines and social networks. As relevant data items from different modalities may convey semantic correlations, it is significant to support cross-modal retrieval, which returns semantically-relevant results from one modality in response to a query of another modality. Recently, a popular and advantageous solution to cross-modal retrieval is learning to hash [1], an approach to approximate nearest neighbors (ANN) search across different modalities with both computation efficiency and search quality. It transforms high-dimensional data into compact binary codes with similar binary codes for similar data, largely reducing the computational burdens of distance calculation and candidates pruning on large-scale high-dimensional data. Although the semantic gap across low-level descriptors and high-level semantics [2] has been reduced by deep learning, the intrinsic heterogeneity across modalities remains another challenge.

Previous cross-modal hashing methods capture the relations across different modalities in the process of hash function learning and transform cross-modal data into an isomorphic Hamming space, where the cross-modal distances can be directly computed [3,4,5,6,7,8,9,10,11,12,13]. Existing approaches can be roughly categorized into unsupervised methods and supervised methods. Unsupervised methods are general to different scenarios and can be trained without semantic labels or relevance information, but they are subject to the semantic gap [2] that high-level semantic labels of an object differ from low-level feature descriptors. Supervised methods can incorporate semantic labels or relevance information to mitigate the semantic gap [2], yielding more accurate and compact hash codes to improve the retrieval accuracy. However, without learning deep representations in the process of hash function learning, existing cross-modal hashing methods cannot effectively close the heterogeneity gap across different modalities.

To improve the retrieval accuracy, deep hashing methods [14,15,16] learn feature representation and hash coding more effectively using deep networks [17, 18]. For cross-modal retrieval, deep cross-modal hashing methods [8, 19,20,21,22,23,24] have shown that deep networks can capture nonlinear cross-modal correlations more effectively and yielded state-of-the-art cross-modal retrieval performance. Existing deep cross-modal hashing methods can be organized into unsupervised methods and supervised methods. The unsupervised deep cross-modal hashing methods adopt identical deep architecture for different modalities, e.g. MMDBM [20] uses Deep Boltzmann Machines, MSAE [8] uses Stacked Auto-Encoders, and MMNN [19] uses Multilayer Perceptrons. In contrast, the supervised deep cross-modal hashing methods [22,23,24] adopt hybrid deep architectures, which can be effectively trained with supervision to ensure best architecture for each modality, e.g. Convolutional Networks for images [17, 18, 25], Multilayer Perceptrons for texts [26,27,28] and Recurrent Networks for audio [29]. The supervised methods significantly outperform the unsupervised methods for cross-modal retrieval.

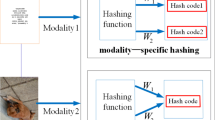
However, most existing methods focus on data compression instead of candidates pruning, i.e., they are designed to maximize retrieval performance by linear scan over the generated hash codes. As linear scan is still costly for large-scale database even using compact hash codes, we may deviate from our original goal towards hashing, i.e. maximizing search speedup under acceptable retrieval accuracy. With the prosperity of powerful hashing methods that perform well with linear scan, we should now return to our original ambition of hashing: enable efficient constant-time search using hash lookups, a.k.n. Hamming space retrieval [30]. More precisely, in Hamming space retrieval, we return data points within a given Hamming radius to each query in constant-time, by hash lookups instead of linear scan. Unfortunately, existing cross-modal hashing methods generally fall short in the capability of concentrating relevant cross-modal pairs to be within a small Hamming ball due to their mis-specified loss functions. This results in their ineffectiveness for cross-modal Hamming space retrieval. The bottleneck of existing cross-modal hashing methods is intuitively depicted in Fig. 1.

Fig. 1.

Illustration of the bottleneck in cross-modal Hamming space retrieval. Different colors denote different categories (e.g. dog, cat, and bird) and different markers denote different modalities (e.g. triangles for images and crosses for texts). Due to the large intrinsic heterogeneity across different modalities, existing cross-modal hashing methods will generate hash codes of different modalities with very large Hamming distances, since their mis-specified losses cannot penalize different modalities of the same category to be similar enough in the Hamming distances, as shown in plot (a). We address this bottleneck by proposing a well-specified pairwise focal loss based on the exponential distribution, which penalizes significantly on similar cross-modal pairs with Hamming distances larger than the Hamming radius, as shown in plot (b). Best viewed in color. (Color figure online)

Towards a formal solution to the aforementioned heterogeneity bottleneck in Hamming space retrieval, this work presents Cross-Modal Hamming Hashing (CMHH), a novel deep cross-modal hashing approach that generates compact and highly concentrated hash codes to enable efficient and effective Hamming space retrieval. The main idea is to penalize significantly on similar cross-modal pairs with Hamming distances larger than the Hamming radius threshold, by designing a pairwise focal loss based on the exponential distribution. CMHH simultaneously learns similarity-preserving binary representations for images and texts, and formally controls the quantization error of binarizing continuous representations to binary hash codes. Extensive experiments demonstrate that CMHH can generate highly concentrated hash codes and achieve state-of-the-art cross-modal retrieval performance for both hash lookups and linear scan scenarios on three benchmark datasets, NUS-WIDE, MIRFlickr-25K, and IAPR TC-12.

2 Related Work

Cross-modal hashing has been an increasingly important and powerful solution to multimedia retrieval [31,32,33,34,35,36]. A latest survey can be found in [1].

Previous cross-modal hashing methods include unsupervised methods and supervised methods. Unsupervised cross-modal hashing methods learn hash functions that encode data to binary codes by training from unlabeled paired data, e.g. Cross-View Hashing (CVH) [4] and Inter-Media Hashing (IMH) [7]. Supervised methods further explore the supervised information, e.g. pairwise similarity or relevance feedbacks, to generate discriminative compact hash codes. Representative methods include Cross-Modal Similarity Sensitive Hashing (CMSSH) [3], Semantic Correlation Maximization (SCM) [11], Quantized Correlation Hashing (QCH) [12], and Semantics-Preserving Hashing (SePH) [37].

Previous shallow cross-modal hashing methods cannot exploit nonlinear correlations across different modalities to effectively bridge the intrinsic cross-modal heterogeneity. Deep multimodal embedding methods [38,39,40,41] have shown that deep networks can bridge different modalities more effectively. Recent deep hashing methods [14,15,16, 42,43,44] have given state-of-the-art results on many image retrieval datasets, but they only support single-modal retrieval. There are several cross-modal deep hashing methods that use hybrid deep architectures for representation learning and hash coding, i.e. Deep Visual-Semantic Hashing (DVSH) [22], Deep Cross-Modal Hashing (DCMH) [23], and Correlation Hashing Network (CHN) [24]. DVSH is the first deep cross-modal hashing method that enables efficient image-sentence cross-modal retrieval, but it does not support the cross-modal retrieval between images and tags. DCMH and CHN are parallel works, which adopt pairwise loss functions to preserve cross-modal similarities and control quantization errors within hybrid deep architectures.

Previous deep cross-modal hashing methods fall short for Hamming space retrieval [30], i.e. hash lookups that discard irrelevant items out of the Hamming ball of a pre-specified small radius by early pruning instead of linear scan. Note that the number of hash buckets will grow exponentially with the Hamming radius and large Hamming ball will not be acceptable. The reasons for inefficient Hamming space retrieval are two folds. First, the existing methods adopt mis-specified loss functions that penalize little when two similar points have large Hamming distance. Second, the huge heterogeneity across different modalities introduces large cross-modal Hamming distances. As a consequence, they cannot concentrate relevant points to be within the Hamming ball with small radius. This paper contrasts from existing methods by novel well-specified loss functions based on the exponential distribution, which shrinks the data points within small Hamming balls to enable effective hash lookups. To our best knowledge, this work is the first deep cross-modal hashing approach towards Hamming space retrieval.

3 Cross-Modal Hamming Hashing

In cross-modal retrieval, the database consists of objects from one modality and the query consists of objects from another modality. We capture the nonlinear correlation across different modalities by deep learning from a training set of $N_x$ images $\{{\varvec{x}}_i\}_{i=1}^{N_x}$ and $N_y$ texts $\{{\varvec{y}}_j\}_{j=1}^{N_y}$, where ${\varvec{x}}_i \in \mathbb {R}^{D_x}$ denotes the $D_x$-dimensional feature vector of the image modality, and ${\varvec{y}}_j \in \mathbb {R}^{D_y}$ denotes the $D_y$-dimensional feature vector of the text modality, respectively. Some pairs of images and texts are associated with similarity labels $s_{ij}$, where $s_{ij} = 1$ implies ${\varvec{x}}_i$ and ${\varvec{y}}_j$ are similar and $s_{ij} = 0$ indicates ${\varvec{x}}_i$ and ${\varvec{y}}_j$ are dissimilar. Deep cross-modal hashing learns modality-specific hash functions $f_x\left( {\varvec{x}} \right) :{\mathbb {R}^{{D_x}}} \mapsto {\left\{ { - 1,1} \right\} ^K}$ and $f_y\left( {\varvec{y}} \right) :{\mathbb {R}^{{D_y}}} \mapsto {\left\{ { - 1,1} \right\} ^K}$ through deep networks, which encode each object ${\varvec{x}}$ and ${\varvec{y}}$ into compact K-bit hash codes ${\varvec{h}}^x = f_x({\varvec{x}})$ and ${\varvec{h}}^y = f_y({\varvec{y}})$ such that the similarity relations conveyed in the similarity pairs $\mathcal{S}$ is maximally preserved. In supervised cross-modal hashing, $\mathcal {S} = \{s_{ij}\}$ can be constructed from the semantic labels of data objects or relevance feedbacks in click-through behaviors.

Definition 1

(Hamming Space Retrieval). For binary codes of K bits, the number of distinct hash buckets to examine is $N\left( {K,r} \right) = \sum \nolimits _{k = 0}^r {\left( {_k^K} \right) }$, where r is the Hamming radius. $N\left( {K,r} \right)$ grows exponentially with r and when $r\le 2$, it only requires O(1) time for each query to find all r-neighbors. Hamming space retrieval refers to the constant-time retrieval scenario that directly returns points in the hash buckets within Hamming radius r to each query, by hash lookups.

Definition 2

(Cross-Modal Hamming Space Retrieval). Assuming there is an isomorphic Hamming space across different modalities, we return objects of one modality within Hamming radius r to a query of another modality, by hash lookups instead of linear scan in the modality-isomorphic Hamming space.

This paper presents Cross-Modal Hamming Hashing (CMHH), a unified deep learning framework for cross-modal Hamming space retrieval, as shown in Fig. 2. The proposed deep architecture accepts pairwise inputs $\{({\varvec{x}}_i, {\varvec{y}}_j, s_{ij})\}$ and processes them through an end-to-end pipeline of deep representation learning and binary hash coding: (1) an image network to extract discriminative visual representations, and a text network to extract good text representations; (2) two fully-connected hashing layers for transforming the deep representations of each modality into K-bit hash codes ${\varvec{h}}^x_i, {\varvec{h}}^y_j \in \{1,-1\}^K$, (3) a new exponential focal loss based on the exponential distribution for similarity-preserving learning, which uncovers the isomorphic Hamming space to bridge different modalities, and (4) a new exponential quantization loss for controlling the binarization error and improving the hashing quality in the modality-isomorphic Hamming space.

3.1 Hybrid Deep Architecture

The hybrid deep architecture of CMHH is shown in Fig. 2. For image modality, we extend AlexNet [17], a deep convolutional network with five convolutional layers conv1–conv5 and three fully-connected layers fc6–fc8. We replace the classifier layer fc8 with a hash layer fch of K hidden units, which transforms the fc7 representation into K-dimensional continuous code ${\varvec{z}}^x_i \in \mathbb {R}^K$ for each image ${\varvec{x}}_i$. We obtain hash code ${\varvec{h}}^x_i$ through sign thresholding ${\varvec{h}}^x_{i} = {\text {sgn}} ({\varvec{z}}^x_i)$. Since it is hard to optimize the sign function due to ill-posed gradient, we adopt the hyperbolic tangent ($\tanh$) function to squash the continuous code ${\varvec{z}}^x_i$ within $[-1,1]$, reducing the gap between the continuous code ${\varvec{z}}^x_i$ and the final binary hash code ${\varvec{h}}^x_i$. For text modality, we follow [23, 24] and adopt a two-layer Multilayer Perceptron (MLP), with the same dimension and activation function as fc7 and fch in the image network. We obtain the hash code ${\varvec{h}}^y_j$ for each text ${\varvec{y}}_j$ also through sign thresholding ${\varvec{h}}^y_{j} = {\text {sgn}} ({\varvec{z}}^y_j)$. To further guarantee the quality of hash codes for efficient Hamming space retrieval, we preserve the similarity between the training pairs $\{({\varvec{x}}_i, {\varvec{y}}_j, s_{ij}): s_{ij} \in \mathcal {S}\}$ and control the quantization error, both performed in an isomorphic Hamming space. Towards this goal, this paper proposes a pairwise exponential focal loss and a pointwise exponential quantization loss, both derived in the Maximum a Posteriori (MAP) framework.

Fig. 2.

The architecture of Cross-Modal Hamming Hashing (CMHH) consists of four modules: (1) a convolutional network for image representation and a multilayer perceptron for text representation; (2) two hashing layers (fch) for hash code generation, (3) an exponential focal loss for learning the isomorphic Hamming space, and (4) an exponential quantization loss for controlling the hashing quality. Best viewed in color.

3.2 Bayesian Learning Framework

In this paper, we propose a Bayesian learning framework to perform deep cross-modal hashing from similarity data by jointly preserving similarity relationship of image-text pairs and controlling the quantization error. Given training pairs with pairwise similarity labels as $\{({\varvec{x}}_i, {\varvec{y}}_j, s_{ij}): s_{ij} \in \mathcal {S}\}$, the logarithm Maximum a Posteriori (MAP) estimation of the hash codes ${\varvec{H}}^x = [{\varvec{h}}^x_1,\ldots ,{\varvec{h}}^x_{N_x}]$ and ${\varvec{H}}^y = [{\varvec{h}}^y_1,\ldots ,{\varvec{h}}^y_{N_y}]$ for $N_x$ training images and $N_y$ training texts is derived as

$$\begin{aligned} \begin{array}{ll} \log P\left( {{\varvec{H}^x}, {\varvec{H}^y}|\mathcal{S}} \right) &{}\propto \log P\left( {\mathcal{S}|{\varvec{H}^x}, {\varvec{H}^y}} \right) P\left( {\varvec{H}^x} \right) P\left( {\varvec{H}^y} \right) \\ &{}= \sum \limits _{{s_{ij}} \in \mathcal{S}} {{w_{ij}}\log P\left( {{s_{ij}}|{{\varvec{h}}^x_i},{{\varvec{h}}^y_j}} \right) } + \sum \limits _{i = 1}^{N_x} {\log P\left( {{{\varvec{h}}^x_i}} \right) } + \sum \limits _{j = 1}^{N_y} {\log P\left( {{{\varvec{h}}^y_j}} \right) } \end{array} \end{aligned}$$

(1)

where $P\left( {\mathcal{S}|{\varvec{H}^x}, {\varvec{H}^y}} \right) = \prod \nolimits _{{s_{ij}} \in \mathcal {S}} {{{\left[ {P\left( {{s_{ij}}|{{\varvec{h}}^x_i},{{\varvec{h}}^y_j}} \right) } \right] }^{{w_{ij}}}}}$ is the weighted likelihood function [45], and $w_{ij}$ is the weight for each training pair $({\varvec{x}}_i, {\varvec{y}}_j, s_{ij})$. For each pair, $P(s_{ij}|{\varvec{h}}^x_i,{\varvec{h}}^y_j)$ is the conditional probability of similarity $s_{ij}$ given a pair of hash codes ${\varvec{h}}^x_i$ and ${\varvec{h}}^y_j$, which can be defined based on the Bernoulli distribution,

$$\begin{aligned} \begin{aligned} P\left( {{s_{ij}}|{{\varvec{h}}^x_i},{{\varvec{h}}^y_j}} \right)&= {\left\{ \begin{array}{ll} \sigma \left( {\text {d} \left( {{\varvec{h}}^x_i, {\varvec{h}}^y_j} \right) } \right) , &{} {s_{ij}} = 1 \\ 1 - \sigma \left( {\text {d} \left( {{\varvec{h}}^x_i, {\varvec{h}}^y_j} \right) } \right) , &{} {s_{ij}} = 0 \\ \end{array}\right. } \\&= \sigma {\left( {\text {d} \left( {{\varvec{h}}^x_i, {\varvec{h}}^y_j} \right) } \right) ^{{s_{ij}}}}{\left( {1 - \sigma \left( {\text {d} \left( {{\varvec{h}}^x_i, {\varvec{h}}^y_j} \right) } \right) } \right) ^{1 - {s_{ij}}}} \\ \end{aligned} \end{aligned}$$

(2)

where $\text {d}\left( {\varvec{h}}^x_i, {\varvec{h}}^y_j \right)$ denotes the Hamming distance between hash codes ${\varvec{h}}^x_i$ and ${\varvec{h}}^y_j$, and $\sigma$ is a probability function to be elaborated in the next subsection. Similar to binary-class logistic regression for pointwise data, we require in Eq. (2) that the smaller $\text {d} \left( {\varvec{h}}^x_i, {\varvec{h}}^y_j \right)$ is, the larger $P\left( {1|{{\varvec{h}}^x_i},{{\varvec{h}}^y_j}} \right)$ will be, implying that the image-text pair ${\varvec{x}}_i$ and ${\varvec{y}}_j$ should be classified as similar; otherwise, the larger $P\left( {0|{{\varvec{h}}^x_i},{{\varvec{h}}^y_j}} \right)$ will be, implying that the image-text pair should be classified as dissimilar. Thus, this is a natural extension of binary-class logistic regression to pairwise classification scenario with binary similarity labels $s_{ij}\in \{0,1\}$.

Motivated by the focal loss [46], which yields state-of-the-art performance for object detection tasks, we focus our model more on hard and misclassified image-text pairs, by defining the weighting coefficient $w_{ij}$ for each pair $({\varvec{x}}_i, {\varvec{y}}_j, s_{ij})$ as

$$\begin{aligned} \begin{aligned} {w_{ij}} = {\left\{ \begin{array}{ll} {\left( {1 - {\sigma \left( {\text {d} \left( {{\varvec{h}}^x_i, {\varvec{h}}^y_j} \right) } \right) }} \right) ^\gamma },\quad &{}{s_{ij}} = 1 \\ {\left( {{\sigma \left( {\text {d} \left( {{\varvec{h}}^x_i, {\varvec{h}}^y_j} \right) } \right) }} \right) ^\gamma },\quad &{}{s_{ij}} = 0 \\ \end{array}\right. } \end{aligned} \end{aligned}$$

(3)

where $\gamma \ge 0$ is a hyper-parameter to control the relative weight for misclassified pairs. In Fig. 3(a), we plot the focal loss with different $\gamma \in [0,5]$. When $\gamma =0$, the focal loss degenerates to the standard cross-entropy loss. As $\gamma$ gets larger, the focal loss gets smaller on the highly confident pairs (easy pairs), resulting in relatively more focus on the less confident pairs (hard and mis-specified pairs).

3.3 Exponential Hash Learning

With the Bayesian learning framework, any probability function $\sigma$ and distance function $\text {d}$ can be used to instantiate a specific hashing model. Previous state-of-the-art deep cross-modal hashing methods, such as DCMH [23], usually adopt the sigmoid function $\sigma \left( x \right) = {1}/({{1 + {e^{ - \alpha x}}}})$ as the probability function, where $\alpha > 0$ is a hyper-parameter controlling the saturation zone of the sigmoid function. To comply with the sigmoid function, we need to adopt inner product as a surrogate to quantify the Hamming distance, i.e. $\mathrm{{d}}\left( {\varvec{h}}^x_i, {\varvec{h}}^y_j \right) = \left\langle {\varvec{h}}^x_i, {\varvec{h}}^y_j \right\rangle$.

However, we discover a key mis-specification problem of the sigmoid function as illustrated in Fig. 3. We observe that the probability of the sigmoid function stays high when the Hamming distance between hash codes is much larger than 2 and only starts to decrease obviously when the Hamming distance becomes close to K/2. This implies that previous deep cross-modal hashing methods are ineffective to pull the Hamming distance between the hash codes of similar points to be smaller than 2, because the probabilities for different Hamming distances smaller than K/2 are not discriminative enough. This is a severe disadvantage of the existing cross-modal hashing methods, which makes hash lookup search inefficient. Note that for each query in the Hamming space retrieval, we can only return objects within the Hamming ball with a small radius (e.g. 2).

Fig. 3.

[Focal Loss] The values of the focal loss (a) with respect to the conditional probability of similar data points ($s_{ij} = 1$). [Exponential Distribution] The values of Probability (b) and Loss (c) with respect to Hamming Distance between the hash codes of similar data points ($s_{ij} = 1$). The Probability (Loss) based on sigmoid function is large (small) even for Hamming distance much larger than 2, which is ill-specified for Hamming space retrieval. As a desired property, our loss based on the exponential distribution penalizes significantly on similar data pairs with larger Hamming distances.

Towards the aforementioned mis-specification problem of sigmoid function, we propose a novel probability function based on the exponential distribution:

$$\begin{aligned} \sigma \left( \text {d} \left( {\varvec{h}}^x_i, {\varvec{h}}^y_j \right) \right) = \exp \left( { - \beta \cdot {\text {d} \left( {\varvec{h}}^x_i, {\varvec{h}}^y_j \right) }} \right) , \end{aligned}$$

(4)

where $\beta$ is the scaling parameter of the exponential distribution, and $\text {d}$ is the Hamming distance. In Fig. 3(b), (c), the probability of the exponential distribution decreases very fast when the Hamming distance gets larger than 2, and the similar points will be pulled to be within small Hamming radius. The decaying speed of the probability will be even faster by using a larger $\beta$, which imposes more force to concentrate similar points to be within small Hamming balls. Thus the scaling parameter $\beta$ is crucial to control the tradeoff between precision and recall. By simply varying $\beta$, we can support a variety of Hamming space retrieval scenarios with different Hamming radiuses for different pruning ratios.

As discrete optimization of Eq. (1) with binary constraints ${\varvec{h}}^*_i\in \{-1,1\}^K$ is challenging, continuous relaxation is applied to the binary constraints for ease of optimization, as adopted by most previous hashing methods [1, 16, 23]. To control the quantization error $\Vert {\varvec{h}}^*_i - {\text {sgn}}({\varvec{h}}^*_i)\Vert$ caused by continuous relaxation and to learn high-quality hash codes, we propose a novel prior distribution for each hash codes ${\varvec{h}}^*_i$ based on a symmetric variant of the exponential distribution as

$$\begin{aligned} P\left( {{{\varvec{h}}^*_i}} \right) = \exp \left( { - \lambda \cdot \mathrm{{d}}\left( {\left| {{{\varvec{h}}^*_i}} \right| ,{\varvec{1}}} \right) } \right) , *\in \{x,y\}, \end{aligned}$$

(5)

where $\lambda$ is the scaling parameter of the symmetric exponential distribution, and ${\varvec{1}} \in \mathbb {R}^K$ is the vector of ones. By using the continuous relaxation, we need to replace the Hamming distance with its best approximation on continuous codes. Here we adopt Euclidean distance as the approximation of Hamming distance,

$$\begin{aligned} \text {d}\left( {{{\varvec{h}}^x_i},{{\varvec{h}}^y_j}} \right) = \left\| {{{\varvec{h}}^x_i} - {{\varvec{h}}^y_j}} \right\| _2^2. \end{aligned}$$

(6)

By taking Eqs. (2)–(5) into the MAP estimation in (1), we obtain the optimization problem of the proposed Cross-Modal Hamming Hashing (CMHH):

$$\begin{aligned} \mathop {\min }\limits _\varTheta L + \lambda Q, \end{aligned}$$

(7)

where $\lambda$ is a hyper-parameter to trade-off the exponential focal loss L and the exponential quantization loss Q, and $\varTheta$ denotes the set of network parameters to be optimized. Specifically, the proposed exponential focal loss L is derived as

$$\begin{aligned} \begin{aligned} L = \sum \limits _{{s_{ij}} \in \mathcal{S}}&\left[ { {s_{ij}}{{\left( {1 - \exp \left( { - \beta \mathrm{{d}}\left( {{\varvec{h}}_i^x,{\varvec{h}}_j^y} \right) } \right) } \right) }^\gamma }\beta \mathrm{{d}}\left( {{\varvec{h}}_i^x,{\varvec{h}}_j^y} \right) } \right. \\ -&\left. \left( {1 - {s_{ij}}} \right) {\left( {\exp \left( { - \beta \mathrm{{d}}\left( {{\varvec{h}}_i^x,{\varvec{h}}_j^y} \right) } \right) } \right) ^\gamma }\log \left( {1 - \exp \left( { - \beta \mathrm{{d}}\left( {{\varvec{h}}_i^x,{\varvec{h}}_j^y} \right) } \right) } \right) \right] , \end{aligned} \end{aligned}$$

(8)

and similarly, the proposed exponential quantization loss is derived as

$$\begin{aligned} Q = \sum \nolimits _{i = 1}^{{N_x}} { \mathrm{{d}}\left( {\left| {{\varvec{h}}_i^x} \right| ,{\varvec{1}}} \right) } + \sum \nolimits _{j = 1}^{{N_y}} { \mathrm{{d}}\left( {\left| {{\varvec{h}}_j^y} \right| ,{\varvec{1}}} \right) }, \end{aligned}$$

(9)

where $\text {d}(\cdot ,\cdot )$ is the Hamming distance between the hash codes or the Euclidean distance between the continuous codes. Since the quantization error will be controlled by the proposed exponential quantization loss, for ease of optimization, we can use continuous relaxation for hash codes ${\varvec{h}}^*_i$ during training. Finally, we obtain K-bit binary codes by sign thresholding ${\varvec{h}} \leftarrow \text {sgn}({\varvec{h}})$, where $\text {sgn}({\varvec{h}})$ is the sign function on vectors that for $i = 1,\ldots ,K$, $\text {sgn}(h_i) = 1$ if $h_i > 0$, otherwise $\text {sgn}(h_i) = -1$. Note that, since we have minimized the quantization error during training, the final binarization step will incur negligible loss of retrieval accuracy.

4 Experiments

We conduct extensive experiments to evaluate the efficacy of the proposed CMHH with several state-of-the-art cross-modal hashing methods on three benchmark datasets: NUS-WIDE [47], MIRFlickr-25K [48] and IAPR TC-12 [49].

4.1 Setup

NUS-WIDE [47] is a public image dataset containing 269,648 images. Each image is annotated by some of the 81 ground truth concepts (categories). We follow similar experimental protocols as [8, 50], and use the subset of 195,834 image-text pairs that belong to some of the 21 most frequent concepts.

MIRFlickr-25K [48] consists of 25,000 images coupled with complete manual annotations, where each image is labeled with some of the 38 concepts.

IAPR TC-12 [49] consists of 20,000 images with 255 concepts. We follow [23] to use the entire dataset, with each text represented as a 2912-dimensional bag-of-words vector.

We follow dataset split as [24]. In NUS-WIDE, we randomly select 100 pairs per class as the query set, 500 pairs per class as the training set and 50 pairs per class as the validation set, with the rest as the database. In MIRFlickr-25K and IAPR TC-12, we randomly select 1000 pairs as the query set, 4000 pairs as the training set and 1000 pairs as the validation set, with the rest as the database.

Following standard protocol as in [11, 23, 24, 37], the similarity information for hash learning and for ground-truth evaluation is constructed from semantic labels: if the image i and the text j share at least one label, they are similar and $s_{ij}=1$; otherwise, they are dissimilar and $s_{ij}=0$. Note that, although we use semantic labels to construct the similarity information, the proposed approach CMHH can learn hash codes when only similarity information is available.

We compare CMHH with eight state-of-the-art cross-modal hashing methods: two unsupervised methods IMH [7] and CVH [4] and six supervised methods CMSSH [3], SCM [11], SePH [37], DVSH [22], CHN [24] and DCMH [23], where DVSH, CHN and DCMH are deep cross-modal hashing methods.

To verify the effectiveness of the proposed CMHH approach, we first evaluate the comparison methods in the general setting of cross-modal retrieval widely adopted by previous methods: using linear scan instead of hash lookups. We follow [23, 24, 37] and adopt two evaluation metrics: Mean Average Precision (MAP) with MAP@R = 500, and precision-recall curves (P@R).

Then we evaluate Hamming space retrieval, following evaluation methods in [30], consisting of two consecutive steps: (1) Pruning, to return data points within Hamming radius 2 for each query using hash lookups; (2) Scanning, to re-rank the returned data points in ascending order of their distances to each query using the continuous codes. To evaluate the effectiveness of Hamming space retrieval, we report two standard evaluation metrics to measure the quality of the data points within Hamming radius 2: Precision curves within Hamming Radius 2 (P@H$\le$2), and Recall curves within Hamming Radius 2 (R@H$\le$2).

For shallow hashing methods, we use AlexNet [17] to extract 4096-dimensional deep fc7 features for each image. For all deep hashing methods, we directly use raw image pixels as the input. We adopt AlexNet [17] as the base architecture, and implement CMHH in TensorFlow. We fine-tune the ImageNet-pretrained AlexNet and train the hash layer. For the text modality, all deep methods use tag occurrence vectors as the input and adopt a two-layer Multilayer Perceptron (MLP) trained from scratch. We use mini-batch SGD with 0.9 momentum and cross-validate the learning rate from $10^{-5}$ to $10^{-2}$ with a multiplicative step-size ${10}^{\frac{1}{2}}$. We fix the mini-batch size as 128 and the weight decay as 0.0005. We select the hyper-parameters $\lambda$, $\beta$ and $\gamma$ of the proposed CMHH by cross-validation. We also select the hyper-parameters of each comparison method by cross-validation.

Table 1. Mean Average Precision (MAP) of all methods for cross-modal retrieval.

Fig. 4.

Precision-recall (P@R) (a) (d), Precision within Hamming Radius 2 (P@H$\le$2) (b) (e) and Recall within Hamming Radius 2 (R@H$\le$2) (c) (f) on NUS-WIDE @ 32 bits.

4.2 General Setting Results

The MAP results of all the comparison methods are demonstrated in Table 1, which shows that the proposed CMHH substantially outperforms all the comparison methods by large margins. Specifically, compared to SCM, the best shallow cross-modal hashing method with deep features as input, CMHH achieves absolute increases of 5.3%/7.9%, 12.5%/19.0% and 4.6%/8.5% in average MAP for two cross-modal retrieval tasks $I$ $\rightarrow$ $T$/$T$ $\rightarrow$ $I$ on NUS-WIDE, MIRFlickr-25K, and IAPR TC-12 respectively. CMHH outperforms DCMH, the state-of-the-art deep cross-modal hashing method, by large margins of 3.5%/4.3%, 2.9%/2.6% and 5.0%/1.4% in average MAP on the three benchmark datasets, respectively. Note that, compared to DVSH, the state-of-the-art deep cross-modal hashing method with well-designed architecture for image-sentence retrieval, CMHH still outperforms DVSH of 2.2%/4.7% in average MAP for two retrieval tasks on image-sentence dataset, IAPR TC-12. This validates that CMHH is able to learn high-quality hash codes for cross-modal retrieval based on linear scan.

The proposed CMHH improves substantially from the state-of-the-art DVSH, CHN and DCMH by two key perspectives: (1) CMHH enhances deep learning to hash by the novel exponential focal loss motivated from the Weighted Maximum Likelihood (WML), which puts more focus on hard and misclassified examples to yield better cross-modal search performance. (2) CMHH learns the isomorphic Hamming space and controls the quantization error, which better approximates the cross-modal Hamming distance and learns higher-quality hash codes.

The cross-modal retrieval results in terms of Precision-Recall curves (P@R) on NUS-WIDE and MIRFlickr-25K are shown in Figs. 4(a), (d) and 5(a), (d), respectively. CMHH significantly outperforms all comparison methods by large margins with different lengths of hash codes. In particular, CMHH achieves much higher precision at lower recall levels or at smaller number of top returned samples. This is desirable for precision-first retrieval in practical search systems.

4.3 Hamming Space Retrieval Results

The Precision within Hamming Radius 2 (P@H$\le$2) is very crucial for Hamming space retrieval, as it only requires O(1) time for each query and enables very efficient candidates pruning. As shown in Figs. 4(b), (e), 5(b) and (e), CMHH achieves the highest P@H$\le$2 performance on the benchmark datasets with regard to different code lengths. This validates that CMHH can learn much compacter and highly concentrated hash codes than all comparison methods and can enable more efficient and accurate Hamming space retrieval. Note that most previous hashing methods achieve worse retrieval performance with longer code lengths. This undesirable effect arises since the Hamming space will become increasingly sparse with longer code lengths and fewer data points will fall in the Hamming ball of radius 2. It is worth noting that CMHH achieves a relatively mild decrease or even an increase in accuracy using longer code lengths, validating that CMHH can concentrate hash codes of similar points together to be within Hamming radius 2, which is beneficial to Hamming space retrieval.

The Recall within Hamming Radius 2 (R@H$\le$2) is more critical in Hamming space retrieval, since it is possible that all data points will be pruned out due to the highly sparse Hamming space. As shown in Fig. 4(c), (f), 5(c) and (f), CMHH achieves the highest R@H$\le$2 results on both benchmark datasets with different code lengths. This validates that CMHH successfully concentrates more relevant points to be within the Hamming ball of radius 2.

It is important to note that, as the Hamming space becomes sparser using longer hash codes, most hashing baselines incur intolerable performance drop on R@H$\le$2, i.e. their R@H$\le$2 approaches zero! This special result reveals that existing cross-modal hashing methods cannot concentrate relevant points to be within Hamming ball with small radius, which is key to Hamming space retrieval. By introducing the novel exponential focal loss and exponential quantization loss, the proposed CMHH incurs very small performance drop on R@H$\le$2 as the hash codes become longer, showing that CMHH can concentrate more relevant points to be within Hamming ball with small radius even using longer code lengths. The ability to adopt longer codes gives CMHH the flexibility to tradeoff accuracy and efficiency, while this is impossible for all previous cross-modal hashing methods.

Fig. 5.

Precision-recall (P@R) (a) (d), Precision within Hamming Radius 2 (P@H$\le$2) (b) (e) and Recall within Hamming Radius 2 (R@H$\le$2) (c) (f) on MIRFlickr @ 32 bits.

4.4 Empirical Analysis

Ablation Study. We investigate three variants of CMHH: (1) CMHH-E is the variant by replacing the exponential focal loss with the popular cross-entropy loss [23]; (2) CMHH-F is the variant without using the focal reweight, namely $w_{ij} = 1$ in Eq. (3); (3) CMHH-Q is the variant without using the exponential quantization loss (9), namely $\lambda$=0; The MAP results of the three variants on the three datasets are reported in Table 2 (general setting by linear scan).

Exponential Focal Loss. (1) CMHH outperforms CMHH-E by margins of 2.7%/3.9%, 2.4%/2.1% and 3.6%/1.2% in average MAP for cross-modal retrieval on NUS-WIDE, MIRFlickr-25K and IAPR TC-12, respectively. The exponential focal loss (8) leverages the exponential distribution to concentrate relevant points to be within small Hamming ball to enable effective cross-modal retrieval, while the sigmoid cross-entropy loss cannot achieve this desired effect. (2) CMHH outperforms CMHH-F by margins of 2.0%/2.8%, 2.5%/2.1% and 2.2%/2.8% in average MAP for cross-modal tasks on the three datasets. The exponential focal loss enhances deep hashing by putting more focus on the hard and misclassified examples, and obtain better cross-modal search accuracy.

Table 2. Mean Average Precision (MAP) comparison of different CMHH variants.

Fig. 6.

Histogram of Hamming distances on similar pairs @ 64 bits of CMHH & DCMH.

Exponential Quantization Loss. CMHH outperforms CMHH-Q by 1.9% /2.2%, 1.7%/ 2.0% and 2.6%/2.3% on the three datasets, respectively. These results validate that the exponential quantization loss (9) can boost the pruning efficiency and improve the performance of constant-time cross-modal retrieval.

Statistics Study. We compute the histogram of Hamming distances (0–64 for 64 bits codes) over all cross-modal pairs with $s_{ij}=1$, as shown in Fig. 6. Due to the large heterogeneity across images and texts, the cross-modal Hamming distances computed based on the baseline DCMH hash codes are generally much larger than the Hamming ball radius (typically 2). This explains its nearly zero R@H$\le$2 in Figs. 4 and 5. In contrast, the majority of the cross-modal Hamming distances computed based on our CMHH hash codes are smaller than the Hamming ball radius, which enables successful cross-modal Hamming space retrieval.

5 Conclusion

This paper establishes constant-time cross-modal Hamming space retrieval by presenting a novel Cross-Modal Hamming Hashing (CMHH) approach that can generate compacter and highly concentrated hash codes. This is done by jointly optimizing a novel exponential focal loss and an exponential quantization loss in a Bayesian learning framework. Experiments show that CMHH yields state-of-the-art cross-modal retrieval results for Hamming space retrieval and linear scan scenarios on the three datasets, NUS-WIDE, MIRFlickr-25K, and IAPR TC-12.