Learning Priors for Semantic 3D Reconstruction

Abstract

We present a novel semantic 3D reconstruction framework which embeds variational regularization into a neural network. Our network performs a fixed number of unrolled multi-scale optimization iterations with shared interaction weights. In contrast to existing variational methods for semantic 3D reconstruction, our model is end-to-end trainable and captures more complex dependencies between the semantic labels and the 3D geometry. Compared to previous learning-based approaches to 3D reconstruction, we integrate powerful long-range dependencies using variational coarse-to-fine optimization. As a result, our network architecture requires only a moderate number of parameters while keeping a high level of expressiveness which enables learning from very little data. Experiments on real and synthetic datasets demonstrate that our network achieves higher accuracy compared to a purely variational approach while at the same time requiring two orders of magnitude less iterations to converge. Moreover, our approach handles ten times more semantic class labels using the same computational resources.

I. Cherabier and J. L. Schönberger—These authors share first authorship.

1 Introduction

Estimating 3D geometry from images is one of the long-standing goals in computer vision. Despite its long history, however, many problems remain unsolved. In particular, ambiguities arising from textureless or reflective regions, viewpoint changes, and image noise render the problem difficult. Powerful priors are therefore needed to robustly solve the task. One source of prior knowledge which can be exploited are semantics and their interaction with 3D geometry. Consider an urban scene, for example. While the ground is often flat and horizontal, building walls are mostly vertical and located on top of the ground. The availability of reliable semantic image classification methods has therefore recently driven the development of methods that jointly optimize geometry and semantics in 3D.

Fig. 1.

Semantic 3D reconstruction results. We learn semantic and geometric neighborhood statistics to handle large amounts of noise, outliers, and missing data. Compared to traditional TV-L1 and the state of the art [12], our approach requires significantly less iterations and memory. Besides, it handles much larger label sets.

In their pioneering work, Häne et al. [10, 12, 13] proposed a method for joint volumetric 3D reconstruction and semantic segmentation using depth maps and semantic segmentations as input. They formulate the task as a variational multi-label problem, where each voxel is labeled by either one of the semantic classes or free space. Wulff shapes [28] serve as convex anisotropic regularizers, modeling the relationship between any two neighboring voxel labels. While impressive semantic reconstruction results have been demonstrated, the priors used are hand-tuned and very simplistic, thus not able to fully capture the complex semantic and geometric dependencies of our 3D world. Furthermore, inference in those models requires thousands of iterations for convergence, limiting the applicability of these methods.

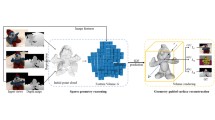
This work revisits the problem of jointly estimating geometry and semantics in a multi-view 3D reconstruction setting as shown in Fig. 1. Our approach combines the advantages of classical variational approaches [10, 12, 13] with recent advances in deep learning [32, 39], resulting in a method that is simple, generic, and substantially more scalable than previous solutions. In addition, our approach allows for automatically learning 3D representations from much fewer training data than existing learning-based solutions. As a result, our approach runs orders of magnitude faster than variational methods while producing better reconstructions. Moreover, memory requirements are significantly reduced allowing for larger label spaces. In summary, we make the following contributions:

• We present a novel framework for multi-view semantic 3D reconstruction which unifies the advantages of variational methods with those of deep neural networks, resulting in a simple, generic, and powerful model.

• We propose a multi-scale optimization strategy which accelerates inference, increases the receptive field, and allows long-distance information propagation.

• Compared to existing variational reconstruction methods [13], our approach learns semantic and geometric relationships end-to-end from data. Compared to fully convolutional architectures, our model is lightweight and can be trained from as little as five scenes without overfitting. Besides, formerly required manual and scene-dependent parameter tuning is no longer necessary and all meta-parameters, such as step sizes, are learned implicitly.

• Our experiments demonstrate that our method is able to achieve high quality results with only 50 unrolled optimization iterations compared to several thousands of iterations using traditional variational optimization.

2 Related Work

Our work builds on a variety of computer vision and machine learning works. This section and Table 1 provide an overview of the most relevant prior works.

Table 1. Qualitative comparison of semantic reconstruction methods. Quantities are approximate and categorized into , , .

Semantic 3D Reconstruction. Ladicky et al. [22] presented a model for joint semantic segmentation and stereo matching. They considered simple height-above-ground properties as constraints between semantics and 3D geometry. Kim et al. [17] proposed a conditional random field (CRF) model for labeling the 3D voxel space based on a single RGB-D image and solved the CRF using graph cuts. Joint volumetric 3D reconstruction and semantic segmentation in a multi-view setting has been tackled by Häne et al. [12, 13] using variational optimization. Extensions to this seminal work consider object-class specific shape priors [10, 23], scalable data-adaptive data structures [1], or larger semantic label spaces [5]. Kundu et al. [21] define a conditional random field to jointly infer semantics and occupancy from monocular video sequences.

A common drawback of these methods is that employed priors are either hand-crafted or not rich enough to capture the complex relationships of our 3D world. We propose to combine the advantages of variational semantic multi-view reconstruction with deep learning in an end-to-end trainable model. This leads to more accurate results and faster runtime as hyperparameters, such as the step size, are learned during training. Furthermore, we propose a novel multi-scale optimization scheme which allows to quickly propagate information across large distances and effectively increases the receptive field of the regularizer.

Variational Regularization. Variational energy minimization methods led to great advances when dealing with noise and missing information. A variety of regularizers have been studied in the literature [2,3,4, 27, 28, 42] in the context of different vision problems. Although these regularizers haven proven effective for low-level vision problems [3, 35] and 3D surface reconstruction [12, 19, 31, 41], they are limited in their expressiveness and do not fully capture the statistics of the underlying problem. In this paper, we propose a more expressive variational regularizer which jointly reasons at multiple scales and can be learned from data.

Learned Regularization. Several works combine the benefits of variational inference and deep learning. Early approaches combine proceed in a sequential manner by either learning the data costs for subsequent energy minimization [43] or by further regularizing the network output [14]. In contrast, several very recent works integrate variational regularization directly into neural networks and apply them to 2D image processing tasks, including depth super-resolution [32], denoising [18, 25, 39], deblurring [18], stereo matching [39] and image segmentation [30]. Typically, the individual optimization steps are unrolled and embedded as layers into a neural network. Our work builds upon these ideas and tailors them to the multi-view semantic 3D reconstruction problem using a novel multi-scale neural network architecture for joint geometric and semantic reasoning.

Learned Shape Priors. Recently, deep learning based approaches have been proposed for depth map fusion [15], 3D object recognition [16, 24], or 3D shape completion [6, 8, 9, 36, 38, 40] using dense voxel grids as input. As all these approaches rely on generic 3D convolutional neural network architectures, they require a very large number of parameters and enormous amounts of training data. In contrast, our approach is more light-weight as it explicitly incorporates structural constraints via unrolled variational inference, therefore limiting the number of parameters needed. Although there are recent efforts to change the spatial scalability of these approaches using data-adaptive structures [11, 33, 34, 37], current results are mostly limited to single objects or simple scenes and consider relatively small resolutions. However, none of these works have considered the semantic multi-view 3D reconstruction task which is the focus of this paper. Furthermore, our approach is fully convolutional and thus also scales to very large scenes.

3 Method

Using a generic 3D convolutional neural networks for semantic 3D reconstruction requires enormous amounts of memory and training data. In this paper, we therefore propose a more light-weight alternative which embeds a multi-label optimization task into the layers of a semantic 3D reconstruction network. We first introduce our multi-scale network architecture in Sect. 3.1, followed by a detailed description of the embedded variational problem in Sect. 3.2, and a description of the loss function we use for training the model in Sect. 3.3.

3.1 Network Architecture

The proposed network architecture for semantic 3D reconstruction is illustrated in Fig. 2. The input to our network is a set of semantically labeled depth maps aggregated into a 3D volume of truncated signed distance functions (TSDFs). More specifically, we follow [12] and accumulate per label evidence, e.g., using depth maps from stereo and corresponding semantic image segmentations. As in traditional TSDF fusion, we trace rays from every pixel in each depth map to determine which voxels are occupied or empty. However, instead of using a fixed additive cost, we scale it using the semantic scores at the corresponding pixel. The output of our network is a volumetric semantic 3D reconstruction, where every voxel has one of the semantic class labels or the free space label.

Our network comprises three components (see Fig. 2): an encoder (yellow), the unrolled primal dual optimization layers (blue), and a decoder (orange). Our method reasons at multiple scales which allows for (i) modeling semantic interactions at different scales and (ii) propagating information quickly over larger distances during inference, e.g., to complete missing data. We found that (i) results in higher accuracy while (ii) leads to much faster convergence compared to standard solvers [12, 42]. We now describe the three network components on a high level before providing a detailed derivation in Sect. 3.2.

Data Cost Encoder. At every voxel, the data cost is encoded by TSDFs computed via fused depth maps (e.g., from stereo or Kinect) and semantic scene segmentations (e.g., obtained from a semantic segmentation algorithm). In the first stage of our network, we pre-process this input using a shallow multi-scale neural network with 3 layers. The encoder serves several purposes: first, it normalizes the influence of the different semantic classes with respect to each other and the data term as a whole. Second, it helps in reducing low-level noise in the input. Finally, our multi-scale optimization requires down-sampling of the data cost which we learn automatically using separate encoders per scale. More concretely, starting at the highest resolution, we process the input with a residual unit that has two pairs of convolution-ReLU operations followed by a final convolution without activation. The encoded input is then down-sampled to the next scale using average pooling, followed by the next encoding stage.

Fig. 2.

Proposed network architecture. While the boxes represent data entities, the blue circles represent concurrent primal-dual (PD) processing steps with the iteration number as subscript. The weights $W_i^j$ indicate the information flow (adjoint, primal and dual variables are omitted for brevity). The graph shows an example of our multi-scale optimization for three scales, however, their number is flexible. (Color figure online)

Unrolled Multi-grid Primal Dual. Instead of processing the input with a high-capacity 3D convolutional neural network, we propose to exploit variational optimization for semantic 3D reconstruction as a light-weight regularizer in our model. The advantage of such a regularizer is that it requires relatively few parameters due to temporal weight sharing while being able to propagate information over large distances by unrolling the algorithm for a fixed number of iterations and propagating information across multiple scales. More specifically, we unroll the iterations of the primal-dual (PD) algorithm of Pock and Chambolle [29], tailored to the multi-label semantic 3D reconstruction task, and parameterize it by replacing the gradient operator with matrices which model the interaction of semantics and geometry at multiple scales for efficient label propagation. Each PD update equation defines a layer in the network, as illustrated with the blue circles in Fig. 2. To learn the parameters of the semantic label interactions and the hyper-parameters of the optimization algorithm, we back-propagate their gradients through the unrolled PD algorithm. A detailed derivation of our algorithm is presented in Sect. 3.2.

Probability Decoder. Similar to the proposed encoding stage, we also decode the obtained solution after the final PD iteration. The main goal here is to smooth and increase contrast, enabling stronger decisions on the final labeling and thereby improving accuracy. Our decoder takes the primal variable after the final iteration of the variational optimizer and feeds it into a residual unit with two pairs of convolution-ReLU operations followed by a final convolution with softmax activation for normalization.

Fig. 3.

Overview of hand-crafted regularizers that have been used in volumetric 3D reconstruction, e.g. weighted TV-Norm: [19, 41], Anisotropic TV: [20, 31], Wulff-shapes: [1, 12]. The polar plots show the smoothness cost $\phi _\mathbf {x}(\cdot )$ for different gradient directions $\nabla u$. The right two cost functions are aligned to a given normal ${\varvec{n}}$. We learn these regularization functions from the training data.

3.2 Learning Variational Energy Minimization

This section describes the multi-grid primal-dual optimization algorithm which we leverage as light-weight, learned regularizer in our network. The traditional variational approach to volumetric 3D reconstruction [1, 10, 12, 13, 19, 20, 31] minimizes the energy

$$\begin{aligned} \mathop {\text {minimize}}_u\int _\varOmega \big ( \!\!\!\!\! \underbrace{\phi _\mathbf {x}(u)}_{\text {regularization}} \!+\! \underbrace{fu}_{\text {data fidelity}} \!\!\!\!\! \big ) \;d\mathbf {x} \quad \text {subject to} \quad \forall \mathbf {x}\!\in \!\varOmega : \sum \nolimits _{\ell } u_\ell \left( \mathbf {x}\right) \!=\! 1 \end{aligned}$$

(1)

in order to find the best labeling $u: \varOmega \rightarrow [0,1]^{|\mathcal {L}|}$ that assigns each point in space a probability for each label $\ell \in \mathcal {L}$. The constraint in (1) ensures normalized probabilities across all labels $\ell \in \mathcal {L}$ at every point $\mathbf {x}\in \varOmega$. The data cost term $f: \varOmega \rightarrow \mathbb {R}^{|\mathcal {L}|}$ aggregates the noisy depth measurements of likely surface locations and is usually modeled as a truncated signed distance function (TSDF). To deal with noise, outliers, and missing data, a regularization term is typically added to the energy functional to obtain a smoother and more complete solution. The simplest choice for regularization is the total variation (TV) norm [2, 4] $\phi _\mathbf {x}(u) = \lambda g(\mathbf {x}) \Vert \nabla u(\mathbf {x}) \Vert _2$ which corresponds to minimizing the surface area of a 3D shape [19]. In most cases the weight function $g: \varOmega \rightarrow \mathbb {R}_{\ge 0}$ encodes photoconsistency measures to align the surface with the input data. In many works this model has been extended to better deal with fine geometric details [20, 27, 31] or multiple semantic labels and directional statistical priors [12, 42]. Figure 3 provides an overview of various regularizers which have been proposed for 3D reconstruction. Notably, all these regularizers are convex and a global minimizer of Eq. (1) can be computed efficiently [3]. These hand-crafted regularizers are usually designed for tractability during optimization, but are not powerful enough to represent the true statistics of the underlying problem [18].

Proposed Energy. To overcome the limitations of hand-crafted regularizers, we follow Vogel and Pock [39] and generalize the gradient operator in the regularizer to the general matrix $W$, i.e. $\phi _\mathbf {x}(u) = \Vert Wu\Vert _2$. Since we are interested in modeling the complete space of directional and semantic interactions in the 3D multi-label setting, we choose to use a 6-dimensional matrix $W\in \mathbb {R}^{2 \times 2 \times 2 \times {|\mathcal {L}|}\times {|\mathcal {L}|}\times 3}$ for our task. This matrix computes gradients using forward-backward differences (modeled by $2 \times 2 \times 2$) and can represent higher-order interactions between any combination of semantic labels (modeled by ${|\mathcal {L}|}\times {|\mathcal {L}|}$) in any spatial direction (modeled by last dimension 3). For $W= \nabla$, we obtain a standard TV regularizer. Note that in contrast to the Wulff shapes used by [12], representing $W$ directly leads to a large reduction in the number of parameters and consequently in memory as evidenced by our experimental evaluation. In this work, we aim to learn the weights of this matrix jointly with the other network parameters considering the following energy minimization problem:

$$\begin{aligned}&\mathop {\text {minimize}}_u\quad \int _\varOmega \big ( \Vert Wu\Vert _2 + fu\big ) \;d\mathbf {x} \quad \text {subject to} \quad \forall \mathbf {x}\!\in \!\varOmega : \sum \nolimits _{\ell } u_\ell \left( \mathbf {x}\right) \!=\! 1 \end{aligned}$$

(2)

Optimization. To minimize the convex energy in Eq. (2), we use a first-order primal-dual (PD) algorithm [3] for which the problem is first transformed into a saddle point problem. We introduce the dual variable $\xi$ to replace the TV-norm with its conjugate. We also relax the constraints in Eq. (1) by introducing the Lagrangian variable $\nu$. Then, the corresponding discretized saddle point energy

$$\begin{aligned} \mathop {\text {minimize}}_u\max _{\Vert \xi \Vert _\infty \le 1} \langle Wu, \xi \rangle + \langle f, u\rangle + \nu \left( \sum \nolimits _{\ell } u_\ell - 1\right) \end{aligned}$$

(3)

can be minimized using the update equations

$$\begin{aligned} 1.\; \nu ^{t+1}&= \nu ^{t} \!+\! \sigma \left( \sum \nolimits _{\ell } \bar{u}_\ell ^{t} - 1\right)&3.\; u^{t+1} \!&=\! \varPi _{\left[ 0, 1\right] } \!\! \left[ u^t\!-\! \tau (W^*\xi ^{t+1}\!+\!f+ \nu ^{t+1}) \right] \nonumber \\ 2.\; \xi ^{t+1}&= \varPi _{\Vert \cdot \Vert \le 1} \left[ \xi ^t+ \sigma W\bar{u}^t\right]&4.\; \bar{u}^{t+1} \!&=\! 2u^{t+1} - u^{t} \end{aligned}$$

(4)

at time $t$ with a total of $T$ iterations, $W^*$ the adjoint of $W$, step sizes $\tau$ and $\sigma$ and projections $\varPi _{[0, 1]}$ and $\varPi _{\Vert \cdot \Vert \le 1}$, see [3]. Note that the operations $W\bar{u}$ and $W^*\xi$ convolve the kernel $W$ with the variables $\xi$ and $\bar{u}$. This enables efficient integration of these operations into a CNN with shared weights across the primal and dual updates and across the different iterations of the algorithm. We embed this algorithm into our network architecture by unrolling it for a fixed number of iterations. The input to the unrolled PD network is the pre-processed data cost term $f$ provided by the encoder and the output is the optimized primal variable $u$ which is passed to the decoder for post-processing.

Optimization Unrolling. One pass on the updates in Eq. (4) corresponds to one PD iteration. Similar to [32], we unroll the PD algorithm for a fixed number of iterations. Each PD update equation defines a layer in the network, as illustrated with the blue circles in Fig. 2. This unrolled PD algorithm constitutes the core of the network that we use to learn the label interactions represented by $W$. Note that the step sizes $\sigma$ and $\tau$ that appear in Eq. (4) influence the speed of convergence of the PD algorithm. These parameters are typically selected manually or by preconditioning [29]. In this work, we learn the step sizes automatically by factoring them into $W$ and thereby eliminating them from the update equations, contributing to fast convergence of the proposed algorithm.

Multi-scale Optimization. In the algorithm discussed above, information only propagates between neighboring voxels, generally resulting in slow convergence of the optimization. Therefore, label interactions are relatively low-level and cannot capture more complex statistics arising at larger scales. While it is easy to enlarge the spatial extent of the matrix $W$, a drawback of naïvely increasing $W$ is the cubic increase in the number of parameters which slows down training and makes the model prone to overfitting. Hence, we consider an alternative in this paper: instead of increasing the size of $W$, we simultaneously consider the scene at multiple scales.

More specifically, at each PD iteration, information is passed from the lower to the higher scales, as shown in Fig. 2. This enables long-range propagation of information and recovery of fine details while at the same time allowing faster back-propagation of gradients during training. Besides, inference runs in parallel at different scales, which, in practice, results in another speedup of the optimization as compared to traditional coarse-to-fine approaches, where the optimization must wait for coarser scales to converge. Note that even with different regularizer matrices $W$ for each scale, the increase in the number of parameters is at most linear in the number of scale levels. Thus, the increase is sub-linear in the receptive field size compared to the cubic increase of the single-scale approach.

In our network, information is propagated via the matrix $W$. Thus, we lift our model to multiple scales by modifying update steps 2 and 3 in Eq. (4) to

$$\begin{aligned} \xi ^{t+1}_{s}= & {} \varPi _{\Vert \cdot \Vert \le 1} \Big [ \xi ^t_{s} + \sigma \big (W_s^s\bar{u}_{s}^t+ U_{s+1}^sW^s_{s+1}\bar{u}^t_{s+1} \big )\Big ]\qquad \end{aligned}$$

(5)

$$\begin{aligned} u^{t+1}_{s}= & {} \varPi _{\left[ 0, 1\right] } \Big [ u_{s}^t+ \tau \big ( W_s^{s*}\xi _{s}^{t+1} + U_{s+1}^{s*} W_{s+1}^{s*}\xi _{s+1}^{t+1} \big ) + \,\tau \left( \nu _{s}^{t+1} - f\right) \Big ] \end{aligned}$$

(6)

where $s$ is one of $S$ scale levels (lower level = higher resolution) and $U_{s+1}^s$ upsamples from $s+1$ to $s$. $W_s^s$ corresponds to the regularizer at level $s$, while $W_{s+1}^s$ handles the transfer of information from level $s+1$ to the next finer level $s$.

3.3 Loss Function

We train the network architecture in Fig. 2 using supervised learning. Towards this goal, we define the training objective as the semantic reconstruction loss between our computed solution $u$ and a given ground truth labeling $\hat{u}$. Typically, this loss is defined as the categorical cross entropy. However, several important modifications to the standard definition of this loss are necessary in practice as the ground truth is often not completely observed or labeled. We follow common practice and introduce a separate label $\tilde{\ell }$ for unlabeled regions. Unobserved regions are modeled by a uniform distribution $\mathcal {U}_\mathcal {L}$ in label space. To make the loss function agnostic to unobserved areas in the ground truth and to not penalize our solution in unlabeled regions, we use the following weighted loss function

$$\begin{aligned} H(u, \hat{u})&= - \int _\varOmega w(\mathbf {x}) \, u(\mathbf {x}) \log \hat{u}(\mathbf {x}) \; d\mathbf {x}\end{aligned}$$

(7)

$$\begin{aligned} w(\mathbf {x})&= \varDelta _{KL}(\hat{u}(\mathbf {x}), \mathcal {U}_\mathcal {L}) \varDelta _{KL}(\hat{u}(\mathbf {x}), \delta _{\tilde{\ell }}) \end{aligned}$$

(8)

which returns zero if the ground truth at $\mathbf {x}$ is not unobserved or unkown. Here, $\varDelta _{KL}$ denotes the KL-divergence. The first term measures the similarity between the ground truth and a uniform distribution and the second term the similarity to a Dirac distribution with center $\tilde{\ell }$. In case the ground truth matches exactly the uniform distribution or it is unlabeled with maximum certainty, this is equivalent to masking the loss as a hard constraint. However, as shown in the experiments, we generate ground truth using conventional regularization methods. As a result, it is beneficial to penalize using a soft constrained loss on the imperfectly labeled ground truth. Without the proposed weighting, the training would receive contradicting supervisory signals. Specifically, if the ground truth is incomplete for a specific class, the loss would encourage reconstruction in the observed areas whereas a potentially correct labeling in the unobserved parts would be inadvertently penalized.

4 Results

This section presents our results. We first analyze the memory and runtime complexity of our method wrt. to the state-of-the-art approach of Häne et al. [12]. Next, we empirically validate our approach in a controlled setting on a synthetic 2D toy dataset Finally, we present results on challenging indoor and outdoor semantic reconstruction tasks.

4.1 Memory and Runtime Complexity

One of the main advantages of our method over Häne et al. [12] is the significantly reduced memory complexity. While the approach of Häne et al. has a memory complexity of $(3+d){|\mathcal {L}|}\cdot |\varOmega | + (1+d){|\mathcal {L}|}^2 |\varOmega |$, ours has a complexity of $(3+d){|\mathcal {L}|}\cdot |\varOmega | + 3\cdot 2^d{|\mathcal {L}|}^2$. Here, $d$ is the dimension of $\varOmega$, and ${|\mathcal {L}|}$ and $|\varOmega |$ the number of labels and voxels. Note that using additional scales in our approach only marginally increases the amount of memory, since each successive higher scale has $2^d$ fewer voxels. While their approach maintain dual variables for all label combinations at each location in the voxel grid, our approach shares this state for all locations. In practice, for a moderate scene size of $|\varOmega |=300^3$ ($500^3$) voxels with ${|\mathcal {L}|}=40$ labels and single-precision floating point data, theirs has an intractable memory usage of around 668 GB (3 TB) versus a tractable 24 GB (111 GB) for ours. In addition to an improved memory complexity, our approach is much faster to compute. Compared to the costly calculation of Wulff shape projections, the convolution operations in our case are much cheaper to compute and, in practice, are implemented efficiently on GPUs. In summary, our proposed approach makes it tractable to perform joint semantic 3D reconstruction for both larger scenes and significantly more labels, as shown in the experiments.

Fig. 4.

2D semantic segmentation on synthetic images. Top Left: 3/1200 test scenes with ground truth (GT), noisy input, results of TV-L1 and ours in comparison. Bottom Left: Reconstruction accuracy for TV-L1 and our method using different numbers of iterations $T$ (TV-L1 converges with 1000) and scales $S$. First row shows accuracy over all pixels, second shows accuracy only over regions with missing data cost. Right: Label transition costs between two labels depending on the surface normal. Ours learns more complex cost functions compared to the hand-crafted ones in Fig. 3. The plots have been rescaled for readability, with the magnitude encoded as color. (Color figure online)

4.2 Experiments on Synthetic 2D Data

Dataset. For validating our model, we created a simple 2D toy dataset with 5 labels, each defined by a color (white for free space, gray for ground, red for building, blue for roof and green for vegetation). The scenes were generated with shapes like boxes, triangles, and circles, which were randomly positioned subject to interval bounds and ordering constraints, e.g., roof on top of building and building on top of ground. We perturb the images with Gaussian noise and simulate missing data by removing large regions using random shapes (circle, square, triangle). Figure 4 shows examples along with their degraded versions. We created 3000 images of size $160 \times 96$ for training and 1200 for testing, respectively. The data cost for label $\ell \in \mathcal {L}$ is defined as $f_\ell = \parallel I- c_\ell \parallel ^2_2$ where $I$ is the input image and $c_\ell$ is the color corresponding to label $\ell$. For regions with missing pixels, which can only be filled by regularization, we use a uniform data cost.

Quantitative Evaluation. Using this dataset, we evaluate the benefit of the multi-scale approach as well as the feature encoding (E) and the probability decoding (D) networks. All networks are trained from random initialization with a batch size of 32. Figure 4 (left) shows results on the test set with TV-L1 as a baseline. We show the accuracy computed on the whole image and only on the missing regions. The latter emphasizes the performance of the regularizer since in these regions, the data cost has no influence. Our approach consistently outperforms TV-L1, especially in the missing regions. This shows that our method learns more powerful regularizers, encoding statistics about geometry and semantics. Furthermore, increasing the number of scales and including encoding and decoding networks is beneficial.

Qualitative Evaluation. Figure 4 (left) compares the segmentations from our full network ($T=20$, $S=3$) to those of TV-L1. While TV-L1 finds the (wrong) minimal surface solution, our network correctly fills in these regions and respects ordering constraints (e.g. building above ground).

Learned Priors. Our network learns costs at label transitions in a small $2^d$ neighborhood at every scale. This cost is influenced by the orientation of the transitions: vertical transitions between building and ground should be penalized more than horizontal transitions. Figure 4 (right) plots the label transition costs against the surface normal for all label combinations. We see that the regularizer has the desired behavior in most cases, e.g. for building to ground transitions, we see that vertical transitions are penalized the most.

Fig. 5.

Semantic 3D reconstruction results. Left: Input. Middle: Reconstruction results. Our method learns semantic and geometric neighborhood statistics to handle large amounts of noise, outliers and missing data. Compared to TV-L1 and the state-of-the-art [12], it needs significantly less iterations and memory. Right: Hand-crafted shape priors from Häne et al. [12] (top) vs. our learned shape priors (bottom).

4.3 Experiments on Real 3D Data

We now use the best-performing architecture as determined in our 2D experiments and apply it to the 3D multi-label domain using two challenging datasets. We show that we can replicate hand-crafted Wulff shapes by learning from solutions produced by Häne et al. [12]. Using the learned weights, our approach produces equivalent results but two orders of magnitude faster, using only a fraction of the memory. Moreover, we apply our method to datasets with ten times more labels than can be handled by existing Wulff shape approaches.

Datasets. For all datasets, we assume gravity aligned inputs and use a standard multi-label TSDF for data cost aggregation [12]. For comparing against Häne et al. [13], we use their 3 outdoor scenes (Castle, South Building, Providence) with 5 labels (freespace, ground, building, vegetation, unkown). The largest scene has a size of around $300^3$ voxels. In addition, we evaluate on the recently released ScanNet dataset [7], comprising 1513 scenes with fine-grain semantic labeling. We adopt the NYU [26] labeling with 40 classes. Using a voxel resolution of 5 cm, the largest scenes have a size of around $400^3$ voxels.

Training. Our network can optimize arbitrarily sized scenes both during inference and training, as our architecture is fully convolutional. However, due to the increased memory requirements during back-propagation and the computational benefits of batch processing in stochastic gradient descent, we train on fixed-size, random crops of dimension $32^3$ with a batch size of 4 and a learning rate of $10^{-4}$. We perform data augmentation by randomly rotating and flipping around the gravity axis. For all experiments, we unroll the PD algorithm for $T\!=\!50$ iterations using $S\!=\!3$ scales. As our network uses a few parameters as compared to pure learning approaches, overfitting is not a problem for our approach and training typically converges quickly after a few thousand mini batches.

Wulff Shape Comparison. First, we are interested in replacing the more complex and computationally costly Wulff shape approach [12] by learning from data produced by their method. Figure 5 (right) shows the original Wulff shapes by Häne et al. next to our learned shapes at scale $s=0$. The cost shape visualization is equivalent to the synthetic 2D experiments with the difference that here we compute the average shape around the gravity axis. Our method meaningfully learns the hand-crafted shapes, demonstrating that we can replicate the more complex Wulff shape formulation. This is confirmed by a 98% per-class accuracy when evaluating our learned weights on the full scenes wrt. [12]. Figures 1 and 5 show qualitative results for Castle and South Building. Moreover, our results are achieved after 50 iterations and 10 s while their approach requires 2750 iterations and around 4000 s to converge. Next, we demonstrate our method in a setting with an order of magnitude more class labels, which would be computationally intractable for their method [12].

Fig. 6.

3D reconstruction results for ScanNet [7] for different scenes and methods.

Evaluation on ScanNet [7]. For ScanNet we re-integrate the provided depth maps and semantic segmentations using TSDF fusion based on the provided camera poses to establish voxelized ground truth. The resulting data costs provide very strong evidence and we thus use multi-label TV-L1 optimization with $W\!=\! \nabla$. For our evaluation, we also generate weak data costs by only integrating every 50th frame. The objective during training is to recover the high fidelity ground truth generated from the strong data cost using only the weak data cost as input. We train our network using 312 training scenes and evaluate their performance on 156 test scenes. Figure 7 summarizes quantitative results for a reconstruction extracted from the input data cost, a multi-label TV-L1, a coarse-to-fine version of our network, a version of our network without variational regularization (0 iterations), and our proposed multi-scale architecture. Note that ours without regularization is a simple variant of approaches like SSCNet [36] or ScanComplete [6]. We draw the following conclusions: First, running TV-L1 for the same number of iterations as our method results in significantly worse results. Second, running TV-L1 for an order of magnitude more iterations until convergence still performs worse than our method. Third, a naïve coarse-to-fine approach does not converge during training and produces bad reconstructions. Moreover, integrating multi-scale variational regularization into the network significantly improves the completeness of the results. Lastly, a version trained on only 5 scenes attains almost the same overall accuracy as a version trained on the full training dataset, indicating that our model can be trained with very little data. Furthermore, due to the few learned parameters in our network, we achieve the same accuracy for the training and test scenes which demonstrates the generalization power of our model. Figures 1 and 6 show qualitative results for selected scenes. Surprisingly, our method sometimes produces results which are visually more pleasing than the ground truth used for training. We attribute this to the fact that our method can learn correct label interactions from all training data jointly and can then apply this knowledge to a single instance.

Fig. 7.

3D Reconstruction accuracy for ScanNet [7]. Left: Reconstruction extracted from the input data, TV-L1 for 50 and for 500 iterations ($\mathrel {\widehat{=}}$ converged), traditional coarse-to-fine network (C2F), our method with/without multi-scale scheme trained on 312 scenes, ours with multi-scale trained on a subset of only 5 scenes, ours without the unrolled optimization (0 iterations). Right: Per-label accuracies.

5 Conclusion

We presented a novel method for dense semantic 3D reconstruction. By incorporating variational regularization into a neural network, we can learn powerful semantic priors using a limited number of parameters. In stark contrast to purely learning based approaches, our method requires little training data and generalizes to new scenes without overfitting. The proposed multi-scale optimization jointly reasons about semantics and geometry at different scales and enables inference that is an order of magnitude more efficient than the state of the art. Experiments on synthetic and real data demonstrate the benefits wrt. accuracy, runtime, memory consumption, and algorithmic complexity.