Deep Domain Generalization via Conditional Invariant Adversarial Networks

Abstract

Domain generalization aims to learn a classification model from multiple source domains and generalize it to unseen target domains. A critical problem in domain generalization involves learning domain-invariant representations. Let X and Y denote the features and the labels, respectively. Under the assumption that the conditional distribution P(Y|X) remains unchanged across domains, earlier approaches to domain generalization learned the invariant representation T(X) by minimizing the discrepancy of the marginal distribution P(T(X)). However, such an assumption of stable P(Y|X) does not necessarily hold in practice. In addition, the representation learning function T(X) is usually constrained to a simple linear transformation or shallow networks. To address the above two drawbacks, we propose an end-to-end conditional invariant deep domain generalization approach by leveraging deep neural networks for domain-invariant representation learning. The domain-invariance property is guaranteed through a conditional invariant adversarial network that can learn domain-invariant representations w.r.t. the joint distribution P(T(X), Y) if the target domain data are not severely class unbalanced. We perform various experiments to demonstrate the effectiveness of the proposed method.

1 Introduction

With the advances in deep learning in recent years, computer vision has achieved impressive success, e.g., in image classification [1, 2], face recognition [3, 4], and object detection [5]. The mentioned tasks rely on standard supervised learning that assumes that the training and test data follow the same distribution. However, this assumption does not hold in many real-world situations due to various changing factors, such as background noise, viewpoint changes and illumination variation. Such factors can cause biases in the collected datasets [6]. In deep learning, a common approach to eliminating data bias is through fine-tuning a pre-trained network on the target domain with a certain number of labels. However, labeling the data when moving to different new target domains is labor intensive. Domain generalization [7,8,9,10,11,12,13,14,15,16] is proposed to overcome such challenges. Given inputs and the corresponding outputs of multiple source domains, domain generalization aims to learn a domain-invariant feature representation that can generalize well to unseen target domains.

Most existing domain generalization methods learn the invariant feature transformation based on handcrafted features or features extracted from pre-trained deep learning models. Compared to handcrafted features, features extracted from pre-trained neural networks are more discriminative and descriptive. Several domain generalization methods [7,8,9,10,11] have demonstrated the effectiveness of features extracted from neural networks. However, the referenced methods consider the extracted features as input X and use a linear transformation or multilayer perceptrons to model the transformation T(X). Such a learning strategy does not fully explore the advantages of deep neural networks. We argue that learning the invariant feature transformation directly from the original image in an end-to-end fashion will lead to better performance.

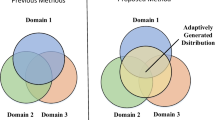
In addition, previous studies assume that the conditional distribution P(Y|X) remains stable across domains and that domain-invariant learning boils down to the guarantee of invariance of the marginal distribution P(T(X)). If this assumption is violated, the joint distribution P(T(X), Y) will not be invariant even if P(T(X)) is invariant after learning. According to recent results in causal learning [17, 18], if the causal structure is $X \rightarrow Y$, where X is the cause and Y is the effect, P(Y|X) can remain stable as P(X) changes because they are “independent" of each other. However, the causal structure is often $Y \rightarrow X$ in computer vision, e.g., object classes are the causes of image features [19]. In this scenario, if P(X) changes, P(Y|X) often changes together with P(X). Considering digital number classification as an example and denoting each rotation angle $\alpha$ as one domain, we obtain a different class-conditional distribution $P(X|Y, {\alpha = \alpha _i})$ for each domain, i.e., the feature distribution of digital numbers depends on the rotation angle. Assuming, for simplicity, that P(Y) does not change, according to the sum rule, we obtain $P(X|\alpha = \alpha _i)=\sum _{j=1}^LP(X|Y=j,\alpha =\alpha _i)P(Y=j)$, where L is the number of classes, and thus, the values of $P(X|\alpha = \alpha _i)$ are different across domains. Additionally, according to Bayes’ rule, $P(Y|X, {\alpha = \alpha _i}) = P(X|Y,{\alpha = \alpha _i})P(Y)/P(X|\alpha = \alpha _i)$; hence, it is very unlikely that $P(Y|X, {\alpha = \alpha _i})$ are the same across domains.

In this paper, we consider the scenario whereby both P(X) and P(Y|X) can change across domains and address domain generalization in an end-to-end deep learning framework. This is achieved by learning a conditional invariant neural network that learns to minimize the discrepancy in P(X|Y) across different domains. Inspired by generative adversarial networks [20] and recent deep domain adaptation methods [21, 22], we develop an adversarial network to learn a domain-invariant representation by making the learned representations on different domains indistinguishable. The conditional invariance property is guaranteed by two adversarial losses that consider the source-domain label information overlooked by the existing methods. One aims to directly make the representations in each class indistinguishable across source domains. The other loss aims to make the representations of all classes indistinguishable across class prior-normalized source domains. The purpose of introducing class prior-based normalization is to reduce the negative effect caused by the possible class prior P(Y) changes across source domains. If the prior distributions P(Y) in the target domain and the pooled source domains are identical, our method can guarantee the invariance of the joint distribution P(X, Y) across domains.

2 Related Work

Domain generalization has drawn substantial attention in recent years, with various approaches [7,8,9,10,11] having been proposed. Muandet et al. [9] proposed a domain-invariant component analysis that learns an invariant transformation by minimizing dissimilarity among domains. Ghifary et al. [8] proposed a unified framework for domain adaptation and generalization using scatter component analysis. In contrast to the above methods, Khosla et al. [7] proposed removing the dataset bias by measuring the dataset-specific model as a combination of the dataset-specific bias and a visual world model. Considering the construction ability of an autoencoder, Ghifary et al. [11] proposed a multi-task autoencoder method to learn domain-invariant features. The learned features could subsequently be used as the input to classifiers. All referenced methods are shallow domain generalization methods that need handcrafted features or features extracted from pre-trained deep learning models. Note that the multi-task autoencoder uses only one hidden layer built on the pre-learned deep features. Such pre-extracted features dramatically constrain the learning ability of the existing domain generalization methods. Our method learns the domain-invariant representation from the original images in an end-to-end deep learning framework.

In addition to the shallow architecture, the existing methods assume that P(Y|X) remains invariant across domains and only aim to learn a domain-invariant feature transformation T(X) to guarantee the invariance of feature distribution P(T(X)). Recent studies of domain adaptation have noted the importance of matching joint distributions instead of the marginal distribution. [23] and [24] suggested considering the domain adaptation problem in the generalized target shift scenario, where the causal direction is $Y \rightarrow X$. In this scenario, both the change of distribution P(Y) and conditional distribution P(X|Y) are considered to reduce the data bias across domains. [22, 25] proposed iterative methods for matching the joint distribution by using the predicted labels from previous iterations as pseudo-labels. [26] proposed an optimal transport-based approach to matching joint distributions and obtained promising results. In contrast to the domain adaptation methods, domain generalization does not require unlabeled data from the target domains.

3 Conditional Invariant Deep Domain Generalization

3.1 Domain Generalization

Suppose the feature and label spaces are represented by $\mathcal {X}$ and $\mathcal {Y}$, respectively. A domain is represented by a joint distribution P(X, Y) defined on $\mathcal {X} \times \mathcal {Y}$. To simplify notation, the m-th domain $P^m(X,Y)$ is denoted $P^m$, and the marginal distribution $P^m(X)$ is denoted $P^m_{X}$. In each domain, we have a sample $\mathcal {D}_m = \{(x_i^m,y_i^m)\}_{i=1}^{N^m}$ drawn from $P^m(X,Y)$, where $N^m$ is the sample size in the m-th domain, while $(x^m_i, y^m_i) \sim P^m(X,Y)$ denotes the i-th data point in the m-th domain. Given C related source domains $\{P^1, P^2,..., P^C \}$ and their corresponding datasets $\mathcal {D}_m = \{(x_i^m,y_i^m)\}_{i=1}^{N^m}$, where $m = \{1,2,...,C\}$, the goal of domain generalization is to learn a model $f: \mathcal {X} \rightarrow \mathcal {Y}$ that can well fit an unseen, yet related, target domain $P^t(X,Y)$ using all data from the source domains.

3.2 Domain Divergence

We first introduce the Jensen-Shannon divergence (JSD) that measures similarities among multiple distributions [27]. We use the marginal distribution P(X) as an example to illustrate the general results in this section. The JSD among distributions $\{P^1(X),P^2(X),\ldots ,P^C(X)\}$ is defined as the average of KL-divergences of each distribution from the average distribution:

$$\begin{aligned} JSD(P^1_X,\ldots ,P^C_X) = \frac{1}{C}\sum \nolimits _{m=1}^C KL(P^m_X||\bar{P}_X),\ \end{aligned}$$

(1)

where $\bar{P}_X=\frac{1}{C}\sum _{m=1}^C P^m_X$ is the average (centroid) of these distributions. In [20], a two-player minimax approach is proposed for learning a generative adversarial network and is proven to be equivalent to minimizing JSD between the generative distribution and data distribution.

We extend the two-player minimax approach to multiple players and prove its equivalence to minimizing the JS divergence among multiple distributions. Denote the distributions after a feature transformation T as $\{P_T^1(T(X)),P_T^2(T(X)),$ $\ldots ,P_T^C(T(X))\}$, or simply as $\{P_T^1,P_T^2,\ldots ,P_T^C\}$. Suppose that D is the learned discriminator and $D^m(T(X))$ denotes the prediction probability with discriminator D that T(X) comes from the m-th domain $P^m_T$, $m \in \{1,2,\ldots ,C\}$. We define the following multi-player minimax game with value function $V(T, D^1,\ldots ,D^C) = \sum \nolimits _{m=1}^C \mathbb {E}_{x\sim P^m(x)}\log {D^m(T(x))}$:

$$\begin{aligned}&\min _T \max _{D^1,D^2,\ldots ,D^C} V(T,D^1,\ldots ,D^C), \nonumber \\&\text {s.t.}~ \sum \nolimits _{m=1}^{C}D^m(T(x))=1. \end{aligned}$$

(2)

In what follows, we will show that the above minimax game reaches a global optimum at $P_T^1=P_T^2=\ldots =P_T^C$, i.e., the multi-player minimax game is able to learn invariant feature representations. The following proposition provides the optimal discriminator under a fixed transformation T.

Proposition 1

Let $x'=T(x)$ for a fixed transformation T; the optimal prediction probabilities $\{D_T^1,\ldots ,D_T^C\}$ of discriminator D are

$$\begin{aligned} D_T^{m*} (x')=P_T^m(x')/\sum \nolimits _{m=1}^{C}P_T^m(x'). \end{aligned}$$

(3)

Proof

For a fixed T, Eq. (2) reduces to maximizing $V(T,D^1,\ldots ,D^C)$ w.r.t. $\{D^1,\ldots ,D^C\}$:

$$\begin{aligned}&\{D_T^{1*},\ldots ,D_T^{C*}\} = \mathop {\mathrm{arg\,max}}\limits _{D^1,\ldots ,D^C}\sum \nolimits _{m=1}^{C}\int _{x'} P_T^m(x')log(D^m(x'))dx' \nonumber \\&~~~~~~~~~~~~~~~~\text {s.t.}~ \sum _{m=1}^{C}D^m(x')=1. \end{aligned}$$

(4)

Maximizing the value function pointwise and applying Lagrange multipliers, we obtain the following problem:

$$\begin{aligned} \{D_T^{1*},\ldots ,D_T^{C*}\} = \mathop {\mathrm{arg\,max}}\limits _{D^1,\ldots ,D^C}\sum \nolimits _{m=1}^{C} P_T^m(x')log(D^m(x')) +\lambda (\sum \nolimits _{m=1}^{C}D^m(x')-1). \end{aligned}$$

Setting the derivative of the above equation w.r.t. $D^m(x')$ to zero, we obtain $D_T^{m*} (x')=-\frac{P_T^m(x')}{\lambda }$. We can solve for the Lagrange multiplier $\lambda$ by substituting $D_T^{m*} (x')=-\frac{P_T^m(x')}{\lambda }$ into the constraint $\sum _{m=1}^{C}D^m(x')=1$ to obtain $\lambda =-\sum _{m=1}^{C}P_T^m(x')$. Thus, we obtain the optimal solution $D_T^{m*} (x')=\frac{P_T^m(x')}{\sum \nolimits _{m=1}^{C}P_T^m(x')}$.

Theorem 1

If U(T) is the maximum value of $V(T,D^1,\ldots ,D^C)$

$$\begin{aligned} U(T) =\sum \nolimits _{m=1}^{C}\mathbb {E}_{x\sim P_T^m(x')}\Big [\log {\frac{p_T^m(x')}{\sum \nolimits _{m=1}^C P_T^m(x')}}\Big ], \end{aligned}$$

(5)

the global minimum of the multi-player minimax game is attained if and only if $P_T^1=P_T^2=\ldots =P_T^C$. At this point, U(T) attains the value $-C\log {C}$.

Proof

If we add $C\log {C}$ to U(T), we obtain

$$\begin{aligned} U(T)+C\log {C} =&\sum \nolimits _{m=1}^{C}\{\mathbb {E}_{x\sim P_T^m(x')}\Big [\log {\frac{p_T^m(x')}{\sum \nolimits _{m=1}^C P_T^m(x')}}\Big ]+\log {C}\}\nonumber \\ =&\sum \nolimits _{m=1}^{C}\mathbb {E}_{x\sim P_T^m(x')}\Big [\log {\frac{p_T^m(x')}{\frac{1}{C}\sum \nolimits _{m=1}^C P_T^m(x')}}\Big ]\nonumber \\ =&\sum \nolimits _{m=1}^{C}KL\Big (P_T^m(x')\Big |\Big |\frac{1}{C}\sum \nolimits _{m=1}^C P_T^m(x')\Big ). \end{aligned}$$

(6)

By using the definition of the JS divergence in Eq. (1), we obtain $U(T) = -Clog{C} + C\cdot JSD(P_T^1,\ldots ,P_T^C).$ As the Jensen-Shannon divergence among multiple distributions is always non-negative and zero iff they are equal, we have shown that $U^*=-C\log {C}$ is the global minimum of U(T) and that the only solution is $P_T^1=P_T^2=\ldots =P_T^C$, i.e., the learned feature representations on all source domains are perfectly matched.

3.3 Proposed Approach

The existing methods proposed matching the marginal distribution P(T(X)) across domains; however, the invariance of P(Y|T(X)) could not be guaranteed. Our approach corrects the changes in P(Y|X) by correcting the changes in P(X|Y). In the ideal scenario, we expect the deep network to learn a conditional invariant feature transformation such that $P^{m=i}(T(X)|Y) = P^{m=j}(T(X)|Y) = P^t(T(X)|Y)$, where $i,j \in \{1,2,...,C\}$, and $P^t$ is a single target domain. With the conditional invariant feature transformation, we can merge all source domains into a single new domain that has the joint distribution $P^{new}(T(X),Y) = P(T(X)|Y) P^{new}(Y)$. While training on the transformed and merged source domain data, we correct the possible class imbalances so that $P^{new}(Y)$ is the same for all classes. Thus, if the target domain data are class balanced, the equality of joint distributions P(T(X), Y) between source domains and target domain can be guaranteed. Even if the target domain data are class unbalanced, our method can still provide reliable results if the features and labels are highly correlated, as the class prior distribution is not important to classification in this case.

The conditional invariance property is achieved by applying the minimax game to different aspects of the distributions on the source domains, resulting in the class-conditional minimax value and class prior-normalized marginal minimax value. In the following section, we will show that such two regularization terms can be easily implemented through variants of softmax loss.

Class-conditional Minimax Value. Suppose that there are L different classes in each domain, and denote by $x^m_{i \sim j}$ an example from the j-th class in the m-th domain. The class-conditional minimax value for class j can be formulated as $V_{con}(T,D_j^1,\ldots ,D_j^C) = \sum \nolimits _{m=1}^C \mathbb {E}_{x\sim P^m(x|y=j)}\log {D_j^m(T(x))}$, where $D_j$ is the discriminator for the j-th image class. The multi-player minimax game is

$$\begin{aligned}&\min _T\max _{D_j^1,\ldots ,D_j^C} V_{con}(T,D_j^1,\ldots ,D_j^C), \nonumber \\&\text {s.t.}~ \sum \nolimits _{m=1}^{C}D_j^m(T(x))=1. \end{aligned}$$

(7)

The empirical minimax game value can be formulated as follows:

$$\begin{aligned} \tilde{V}_{con}(T,D_j^1,\ldots ,D_j^C) = \sum \nolimits _{m=1}^C \frac{1}{N^m_j} \sum \nolimits _{i=1}^{N^m_j} logD_j^m(T(x^m_{i \sim j})), \end{aligned}$$

(8)

where $N^m_j$ denotes the number of examples in the j-th class of the m-th domain. This term computes the minimax game value among P(X|Y) locally. In practice, we compute the minimax game values for all classes separately and subsequently sum such values. By optimizing the above minimax value, we can guarantee the invariance of class-conditional distributions $P(T(X)|Y=j)$ among domains.

Class Prior-Normalized Marginal Minimax Value. If the sample size is not large, overfitting can easily occur in a deep network due to a very large number of parameters. As the number of examples in certain classes is sometimes small, learning with the above class-conditional minimax value can result in overfitting. To improve learning of domain-invariant features, we propose learning a class prior-normalized marginal term that applies the minimax game value to all conditional distributions globally. Note that the marginal distribution of feature representations on the m-th domain can be formulated as

$$\begin{aligned} P^m(T(X)) = \sum \nolimits _{j=1}^L P^m(T(X)|Y=j) P^m(Y=j). \end{aligned}$$

(9)

The above equation shows that the marginal distribution $P^m(T(X)$ is determined by the conditional distribution $P^m(T(X)|Y=j)$ and the class prior distribution $P^m(Y=j)$, where $j \in \{1,2,...,L\}$. As shown in [23, 24], we may be able to determine the conditional invariant representation T(X) by matching the marginal distribution P(T(X)) across domains, i.e., the invariance of P(T(X)) may induce invariance of P(T(X)|Y) if P(Y) is invariant. If P(Y) also changes, even with an invariant P(T(X)|Y) across domains, P(T(X)) can still vary according to Eq. (9). In this case, minimizing the discrepancy in P(X) may lead to removal of useful information, as the effect of changing P(Y) is not supposed to be corrected by learning an invariant representation from X. To remove the effect caused by the changing class prior distribution P(Y), we propose normalizing the class prior distribution as $P_{N}^m(T(X)) = \sum \nolimits _{j=1}^LP^m(T(X)|Y=j)\frac{1}{L}$. The above class prior-normalized distribution $P^m_{N}$ enforces the prior probability for each class to be the same. Consequently, the invariant class conditional distribution across domains can guarantee equality of class prior-normalized marginal distributions across domains. Suppose that $\beta ^m(Y)$ is the normalized weight to ensure that $P_{N}^m(T(X)) = \sum \nolimits _{j=1}^L P^m(T(X)|Y=j) P^m(Y=j) \beta ^m(Y=j) = \sum \nolimits _{j=1}^L P^m(T(X)|Y=j) \frac{1}{L} .$ We apply the minimax game according to the class prior-normalized marginal distribution as follows:

$$\begin{aligned}&\min _T\max _{D^1,\ldots ,D^C}V_{norm}(T,D^1,\ldots ,D^C) \nonumber \\ =&\min _T\max _{D^1,\ldots ,D^C} \sum \nolimits _{m=1}^C \mathbb {E}_{x\sim P_N^m(x)}\log {D^m(T(x))} \nonumber \\ =&\min _T\max _{D^1,\ldots ,D^C} \sum \nolimits _{m=1}^C \mathbb {E}_{x\sim \int P^m(x|y)P^m(y)\beta ^m(y)dy}\log {D^m(T(x))} \nonumber \\ =&\min _T\max _{D^1,\ldots ,D^C} \sum \nolimits _{m=1}^C \int P^m(x|y)P^m(y)\beta ^m(y)dy\log {D^m(T(x))dx}\nonumber \\ =&\min _T\max _{D^1,\ldots ,D^C} \sum \nolimits _{m=1}^C \int P^m(x,y)\log {D^m(T(x))\beta ^m(y)dxdy}\nonumber \\&\text {s.t.}~ \sum \nolimits _{m=1}^{C}D^m(T(x))=1. \end{aligned}$$

(10)

The empirical version of a class prior-normalized minimax value is as follows:

$$\begin{aligned} \tilde{V}_{norm}(T,D^1,\ldots ,D^C) = \sum \nolimits _{m=1}^C \frac{1}{N^m}\sum \nolimits _{i=1}^{N^m}\log {D^m(T(x_i^m))}\beta ^m(y_i^m), \end{aligned}$$

(11)

Fig. 1.

The network architecture of our proposed method. It consists of four parts: feature learning network which represents the invariant feature transformation T, image classification network which classifies the images from all domains with softmax loss, class prior-normalized domain network which discriminates different domains with loss in Eq. (14), and class-conditional domain network which discriminates domains for each image class with loss in Eq. (13).

i.e., the class prior-normalized weight $\beta ^m(y_i^m)$ can be viewed as a weight of the log-likelihood. And $\beta ^m(y_i^m)$ can be empirically obtained as

$$\begin{aligned} \beta ^m(y^m_i) = \frac{1}{L}\frac{1}{P^m(Y=y^m_i)}=\frac{N^m}{L\times N^m_{j=y_i^m}}, \end{aligned}$$

(12)

where $N^m$ denotes the total number of examples in the m-th domain and $N^m_{j=y^m_i}$ denotes the number of examples with the same label as $y^m_i$ in the m-th domain.

4 Conditional Invariant Adversarial Network

We introduce the conditional invariant deep neural network to represent the feature transformation T and then implement the approach proposed in Sect. 3.3. The architecture is shown in Fig. 1. It contains four components: the representation learning network, the image classification network, the class-conditional domain network, and the class prior-normalized domain network. The representation learning network aims to learn a class-conditional domain-invariant feature representation, while retaining the ability to discriminate among different image classes. The two domain classification networks aim to make the features of examples from different domains indistinguishable by adversarial training. Additionally, the image classification network is used to make the learned features informative for classification. In this section, we will introduce each network and describe the process of training such networks using various loss functions.

Let $x_i$ be an input image, $F(\cdot | \theta )$ denote a network with parameter $\theta$, and $F(x_i | \theta )$ be the output of image $x_i$. To simplify notation, the feature representation learning network is denoted $F(\cdot | \theta _f)$ or $F_f(\cdot )$, the image classification network is denoted $F(\cdot | \theta _c)$ or $F_c(\cdot )$, and the class-conditional domain network for image class j is denoted $F^j(\cdot | \theta _d)$ or $F^j_d(\cdot )$. Additionally, the class prior-normalized domain network is denoted $F(\cdot | \theta _p)$ or $F_p(\cdot )$.

4.1 Class-Conditional Domain Classification Network

According to Eq. (7), we can implement the class-conditional minimax game value through a variant of softmax loss. For image class j, the class-conditional domain loss can be formulated as follows:

$$\begin{aligned} L_{con}(\theta _f,\theta _d^j) = \sum \limits _{m=1}^{C} [\frac{1}{N_j^m} \sum _{i=1}^{N^m_j} \sum _{n=1}^C I[y^d_{i \sim j}=n] logP_n(F^j_d(F_f(x^m_{i \sim j})))], \end{aligned}$$

(13)

where $y^d_{i \sim j} \in \{1,2,...,C\}$ denotes the domain label of $x_{i \sim j}$ (i-th example in class j). $P_n(F^j_d(F_f(x_{i \sim j})))$ denotes the predicted probability that the image in j-th category belongs to the n-th domain. Note that the above loss is specifically for the j-th image class. If we have L classes, we must construct L sub-branches of the networks. Each sub-branch corresponds to one class.

4.2 Class Prior-Normalized Domain Classification Network

We introduce the class prior-normalized domain classification networks according to Eq. (11). It is also implemented using a variant of softmax loss. We obtain the prior-normalized loss as

$$\begin{aligned} L_{norm}(\theta _f, \theta _p) = \sum \limits _{m=1}^C \frac{1}{N^m} [\sum \limits _{i=1}^{N^m} \sum \limits _{n=1}^C \beta ^m(y^m_i) I[y_i^d=n] log{{P_n(F_p(F_f(x_i)))}}], \end{aligned}$$

(14)

where $y_i^m$ denotes the class label of the i-th image in domain m.

4.3 Learning Procedure

We combine all the above losses with the image classification loss $L_{cla}(\theta _f,\theta _c)$ used for image classification networks. Note that $L_{cla}(\theta _f,\theta _c)$ can be a standard softmax loss. The total loss can be obtained as follows:

$$\begin{aligned} R(\theta _f,\{\theta ^j_d\}_{j=1}^L,\theta _p, \theta _c) = L_{cla}(\theta _f, \theta _c) + \lambda (\sum \limits _{j=1}^L L_{con}(\theta _f,\theta ^j_d) + L_{norm}(\theta _f, \theta _p))). \end{aligned}$$

(15)

The learning of the above loss can be separated into two steps by determining the optimal values $(\theta ^{*}_{f},\{\theta ^{*j}_d\}_{j=1}^{L},\theta ^{*}_{p}, \theta ^{*}_{c})$ as follows:

$$\begin{aligned} \begin{aligned} (\theta _f^*, \theta _c^*)&= \mathop {\mathrm{arg\,min}}\limits _{\theta _f,\theta _c} R(\theta _f,\{\theta ^j_d\}_{j=1}^L,\theta _p, \theta _c), \\ (\{\theta ^{*j}_d\}_{j=1}^L,\theta _p)&= \mathop {\mathrm{arg\,max}}\limits _{\{\theta ^j_d\}_{j=1}^L,\theta _p} R(\theta _f,\{\theta ^j_d\}_{j=1}^L,\theta _p, \theta _c). \end{aligned} \end{aligned}$$

(16)

A saddle point of the above optimization problem can be determined by performing the following gradient updates iteratively until the networks converge:

$$\begin{aligned} \begin{aligned} \theta _f^{i+1}&= \theta _f^{i} - \gamma [ \frac{\partial {L^i_{cla}}}{\partial {\theta _f}} + \lambda (\sum \nolimits _{j=1}^L\frac{\partial {L^i_{con}(\theta _f,\theta _d^j)}}{\partial {\theta _f}} + \frac{\partial {L^i_{norm}}}{\partial {\theta _f}})], \\ \theta _c^{i+1}&= \theta _c^{i} - \gamma \frac{\partial {L^i_{cla}}}{\partial {\theta _c}}, \\ (\theta ^j_d)^{i+1}&= (\theta ^j_d)^i + \gamma \lambda \frac{\partial {L^i_{con}(\theta _f,\theta _d^j)}}{\partial {\theta ^j_d}}, \\ \theta _p^{i+1}&= \theta _p^i + \gamma \lambda \frac{\partial {L^i_{norm}}}{\partial {\theta _p}}, \end{aligned} \end{aligned}$$

(17)

where $\gamma$ is the learning rate. It is very similar to the stochastic gradient descent (SGD). The only difference is in the updating of $\theta _p$ and $\theta _d^j$, which contain the negative gradients from two domain classification losses. Such negative gradients contribute to making the learned features similar across domains. We propose a gradient-reversal layer (GRL) to update $\theta _f$ by easily following [21]. This gradient-reversal layer does nothing and merely forwards the input to the following layer during forward propagation. However, it multiplies the gradient by $-1$ during the backpropagation to obtain a negative gradient from the domain classification.

5 Experiments

In this section, we conduct experiments on three domain generalization datasets to demonstrate the effectiveness of our conditional invariant deep domain generalization (CIDDG). We compare our proposed method to the following methods.

• L-SVM [29] is support vector machines (SVM) with a linear kernel to classify the learned feature representations.

• Kernel Fisher discriminant analysis (KDA) [30] is used to find a transformation of data using nonlinear kernels in all source domains.

• Undo-bias (UB) [7] measures the model of each task with a domain-specific weight and a globally shared weight used for domain generalization. The original UB was developed for binary domain generalization classification. We extend it to a multi-class method using a one-vs-all strategy.

• Domain-invariant component analysis (DICA) [9] aims at learning a domain-invariant feature representation by matching the marginal distributions across domains.

• Scatter component analysis (SCA) [8] is a unified framework for domain adaptation and domain generalization that also learns a domain-invariant feature transformation through marginal distributions.

• Multi-task auto-encoder (MTAE) [11] is a domain generalization method based on an auto-encoder to match marginal distributions across domains.

• DeepA refers to Deep-All, using data from all source domains to train the networks with only image classification loss.

• DeepD refers to Deep-Domain, using data from all source domains to train the networks with image classification loss and domain classification loss to match the marginal distribution P(T(X)).

• DeepC refers to Deep-Conditional, using data from all source domains to train networks with image classification loss and our proposed class-conditional domain classification loss in Eq. (13).

• DeepN refers to Deep-Normalize, using data from all source domains to train the networks with image classification loss and our proposed class prior-normalized domain classification loss in Eq. (14).

• CIDDG uses data from all source domains to train networks with image classification loss, class-conditional domain classification loss and class prior-normalized domain classification loss, as shown in Eq. (15).

Fig. 2.

Rotated MNIST dataset. Each rotation angle is viewed as one domain.

5.1 Rotated MNIST Dataset

The rotated MNIST digits are shown in Fig. 2, which displays four different rotation angles: $0^{\circ }, 30^{\circ }, 60^{\circ }$ and $90^{\circ }$. Note that the original MNIST digits are already characterized by certain small-angle rotations. Each of the four rotation angles is viewed as one domain. Therefore, we have four domains. One domain is selected as the target domain and the other three ones are used as source domains. We repeat it four times, thus each domain is used as the target domain once. The number of training examples from each class in different domains are randomly chosen from a uniform distribution U[80 160], to guarantee the variance of P(Y) in each domain. The number of test examples is 10000 and they are obtained from the MNIST testset with corresponding rotation angles.

Table 1. Performance comparison in terms of accuracy ($\%$) on rotated MNIST dataset.

Fig. 3.

Feature visualization of different methods on rotated MNIST dataset when the target domain is $90^{\circ }$. Different colors refer to different domains and the gray color denotes the target domain. Different shapes corresponds to different image classes.

The network architecture for rotated MNIST is the same as the architecture in [31]. All domain classification networks consist of three fully-connected layers $(1024\rightarrow 1024 \rightarrow 10 )$ and the GRL layer is connected to the ReLU layer after the last convolution layer. The input features for baseline methods (SVM, KDA, UB, DICA, SCA, MATE) are extracted using the well-trained DeepA network. RBF kernel is applied to KDA, UB, DICA and SCA. Additionally, linear SVM is used to classify the learned domain-invariant features for KDA, DICA, SCA and MATE. Deep-learning-based methods, including DeepA, DeepD, DeepC, DeepN and CIDDG, use softmax layer to do the classification. The experimental results are summarized in Table 1.

Our proposed conditional-invariant adversarial network achieves the best performance when testing on different target domains. All deep-learning-based methods outperform traditional domain generalization methods. Our method can achieve better improvement on more challenging tasks, e.g. the target domain is $0^{\circ }$ or $90^{\circ }$, which demonstrates that our method is more robust. When the target domain is $30^{\circ }$ or $60^{\circ }$, the angle $30^{\circ }$ or $60^{\circ }$ can be interpolated from its corresponding source domains $(0^{\circ },60^{\circ },90^{\circ })$ or $(0^{\circ }, 30^{\circ }, 90^{\circ })$. It is easier to learn a generalized model when testing on an interpolation angle ($30^{\circ }$ or $60^{\circ }$) than testing on an extrapolation angle ($0^{\circ }$ or $90^{\circ }$).

To better understand the generalization ability of different methods, we also visualize the learned feature distribution using t-SNE [32] projection in Fig. 3. We randomly select 100 examples from each class in the target domain for visualization. In the visualization results, DeepA refers to original feature distribution learned by the network with just softmax loss. For DeepA, the feature has been learned to be discriminative but different domains are not well matched. Almost all domain generalization methods can learn better domain-invariant features. Methods like SCA, MATE, DeepD can well match the feature distributions of the source domains; however, the distributions of several classes in the target domain are not well matched. Note that the visualization performance of KDA are not promising, we do not show its visualization result considering the limited pages. For our CIDDG, the distributions of about two classes are not well matched. In genera, our CIDDG can learn more discriminative features, and better match the distributions across source domains and target domains.

5.2 VLCS Dataset

In this section, we conduct experiments on a real world image classification dataset VLCS. It consists of four different sub-datasets corresponding to four domains: PASCAL VOC2007 (V) [33], LabelMe (L) [34], Caltech-101 (C) [35] and SUN09 (S) [36]. Following the settings in previous works [7, 9], we select the five shared classes (bird, car, chair, dog and person) for classification. The total image numbers in the four domains (V,L,C,S) are 3376, 2656, 1415 and 3282 respectively. We use AlexNet [1] to train all the deep learning models and extract the FC6 features as input for traditional baseline methods. All domain classification networks consist of 3 fully-connected layers $(1024\rightarrow 1024\rightarrow 3)$ and the GRL layer is connected to the FC6 layer. The datasets from source domains are split into two parts: $70\%$ for training and $30\%$ for validation, following [11, 28]. The whole target domain is used for testing.

For SVM, KDA, UB, DICA, SCA, MATE, we first directly extract FC6 features of AlexNet from source domains and then learn domain-invariant features using these baseline domain generalization methods. Finally, linear SVM are used to train the classification model and test on target domains. For DeepA, we directly use all source domains to fine-tune the AlexNet and test on target domains. For DeepD, we use all the domains to fine-tune the AlexNet with a domain classification network to match the marginal distribution P(X). DeepC, DeepN and CIDDG are our methods with different proposed losses. The experimental results are summarized in Table 2.

From the results, we can conclude that traditional domain generalization methods perform even worse than DeepA (the network just fine-tuned using all source domains). Deep domain generalization methods outperform the simply fine-tuned model DeepA. Additionally, our conditional-invariant domain generalization method performs better than domain generalization (DeepD) which matches the marginal distribution.

Table 2. Performance comparison in terms of accuracy ($\%$) on VLCS dataset.

Table 3. Performance comparison in terms of accuracy ($\%$) on PACS dataset.

5.3 PACS Dataset

PACS [28] consists of four sub-datasets corresponding to four different image styles, including photo (P), art-painting (A), cartoon (C) and sketch (S). Each image style can be viewed as one domain. The numbers of images in each domain are 1670, 2048, 2344, 3929 respectively. We use all the images from the source domains as train set and test on all the images from the target domain. We extract the features from FC7 layer for traditional methods and the GRL layer is also connected to FC7 layer. Other settings including the network architectures are the same as that used in VLCS dataset.

The results are shown in Table 3. Similar conclusions can be made as that in the experiments of VLCS dataset. The reason DeepN performs worse than DeepC is that PACS has larger data bias and variance of P(Y). The class-conditional domain classification networks cannot learn well with just images in one specific image class and not considering the changes in P(Y) across domains.

6 Conclusions

In this paper, we proposed a novel conditional-invariant deep domain generalization method. This method is superior than previous works because it matches conditional distributions by considering the changes in P(Y) rather than marginal distributions, thus it can better learn domain invariant features. We prove that the distributions of multiple source domains can be perfectly matched with our proposed multi-player minimax value. Additionally, extensive experiments are conducted and the results demonstrate the effectiveness of our proposed method.