Polarimetric Three-View Geometry

Abstract

This paper theorizes the connection between polarization and three-view geometry. It presents a ubiquitous polarization-induced constraint that regulates the relative pose of a system of three cameras. We demonstrate that, in a multi-view system, the polarization phase obtained for a surface point is induced from one of the two pencils of planes: one by specular reflections with its axis aligned with the incident light; one by diffusive reflections with its axis aligned with the surface normal. Differing from the traditional three-view geometry, we show that this constraint directly encodes camera rotation and projection, and is independent of camera translation. In theory, six polarized diffusive point-point-point correspondences suffice to determine the camera rotations. In practise, a cross-validation mechanism using correspondences of specularites can effectively resolve the ambiguities caused by mixed polarization. The experiments on real world scenes validate our proposed theory.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

When an unpolarized incident light is reflected by a dielectric surface, it becomes polarized and the phase of its polarization is characterized by the plane of incidence. This process can be observed by a rotatable polarizer mounted in front of a camera that captures sinusoidally varying pixel-wise radiance, where the readings arising from specular reflection exhibits a $\frac{\pi }{2}$ phase shift relative to the readings from diffusive reflections. In both phenomena, the phase shift of the sinusoids indicates the azimuthal orientation of the surface normal, and its elevation angle is evaluated by the reflection coefficients [13]. Essentially, polarimetric measurements impose a linear constraint on surface normals [43], which is useful for shape estimations under orthographic projection.

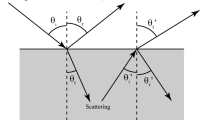
We note that, the relative phase of polarimetric measurements by a triplet of cameras alone encodes sufficient information to describe the relative pose of these cameras. As illustrated in Fig. 1, characterizing general surface reflectance is usually the plane of incidence formed by the incident light and the line of sight. Geometrically these planes are organized in a way to represent reflection/refraction under two common scenarios: (1) direct surface reflection due to a directional light which displays specularities; (2) diffusive reflections due to subsurface scattering that render the surface’s own property. In the first scenario all planes of incidence intersect on a set of parallel lines aligned with incident light, and in the second scenario other planes exist to intersect on the line passing through the surface normal. These pencils of planes impose a geometric constraint on the plane orientations explicitly through the relative rotations of the cameras. Specifically, three planes (e.g. camera poses) uniquely specify the line of intersection.

In the inverse domain, each pencil of planes is represented by a 3-by-3 rank-2 matrix, so accordingly six instances of such matrix are sufficient to determine the camera rotations. However, the number of possible constructions of these matrices grows exponentially due to the $\frac{\pi }{2}$-ambiguity caused by the mixed polarizations [3], hence directly solving the minimal problem is numerically prohibitive. Fortunately, since often the ambiguities occur only when specularities are present, the $\frac{\pi }{2}$ phase shift can be effectively leveraged if we only defer their use for verifications, but not directly for estimations. Specifically, since constructions using incident light are easy to establish, we obtain the corresponding matrices and make additional three attempts for each instance with $\frac{\pi }{2}$ difference, as doing so effectively cross-validates the co-existing constructions induced by surface normal.

To sum up, by estimating the relative rotation of a triple of cameras, in this paper we elucidate a fundamental connection between polarization and three-view geometry. In particular, our contributions are as follows:

• 1. Using microfacet theory, we identify and theorize the ubiquitous existence of two types of a pencil of planes induced by polarizations from general reflectance.

• 2. We formulate a geometric constraints using the induced pencil of planes, under which we show that in a triplet of cameras polarimetric information can be leveraged to extract the cameras’ rotations from its translation.

• 3. We use experiment to validate our theories, in particular, we propose to use correspondences of specular points to address mixed polarizations.

The rest of this paper is organized as follows: Sect. 2 overviews the related work, Sect. 3 explains the polarization from general reflectance using microfacet theory, and by examining the measured relative phase we illustrate the existence of two types of polarization from reflection. Section 4 extends our formulation to three-view geometry, revealing how camera rotation can be decoded from polarimetric information. Our experiments on real world scenes are described in Sect. 5. Section 6 discuss our plan for the future work and concludes this paper.

Fig. 1.

This paper examines two types of polarization-induced geometrical configurations. One is a pencil of planes induced by diffusive reflection which encodes the information about the surface normal, the other is induced by specular reflection and it encodes the light direction

2 Related Works

This work is related to two lines of research: one applies polarization as a visual cue for shape and depth estimation, the other formulates three-view geometry using trifocal tensors.

2.1 Shape and Depth Estimation from Polarization

Following the Fresnel equations [13], ideal mirror reflection allow the azimuth angle and zenith angle of the normal of the mirror surface to be evaluated. This physical model can be generalized to more realistic cases where relaxed assumptions are made for the controlled light, the camera pose, and the reflectance property of the surface. Correctly identifying the orientation of the plane of incidence among multiple ambiguous interpretations is a common challenge that many applications face to address.

Direct shape estimation based on polarization under single view [5, 28] for photometric stereo often targets on a surface of known reflectance under controlled illumination [9, 32]. For example, it is intuitive to recover the shape of a specular surface because specularities always display strong polarization effect [35]. It also reasonable to leverage polarization observed from transparent objects [25, 26], the objects covered by metallic surface [29], or those made of scattering medium [30]. It has been demonstrated that diffusive reflection can carry polarization signals due to subsurface scattering [3]. Shading can be integrated to enhance the estimations [23], and in the presence of mixed polarization, labeling diffusive and specular reflectance [31] turns out to be useful in some applications [38]. Additionally, designed illumination pattern can also be applied to enrich the polarization effect [1].

Another typical example of applying the polarimetric cues is to fuse them to constrain the depth map obtained using other means. The depth signals can either be obtained physically [17, 18] or geometrically inferred [37, 40]. The underlying assumptions made is that the surfaces tend to be smooth or can be easily regulated.

A multi-camera setup produce a richer set shape cues [2, 4], reduce the occurrences of ambiguous measurements, and avoid the formulation involving the refractive index, which is dealt directly in some cases [15, 16]. Polarimetric cues can facilitate the dense two-view correspondence over specular surfaces [6]. In a standard structure-from-motion setting, camera poses are first estimated using the classical approaches before [8, 27] polarimetric information is applied. Recent work also integrates it into SLAM [44]. In our work, we show that polarimetric information can also be applied to retrieve camera pose, which to our knowledge is the first demonstration of its usefulness in the related field.

2.2 Three-View Geometry

Analogous to the role of fundamental matrix in two-view geometry, the three-view geometry is characterized by the trifocal tensor that relates point or line correspondences across three views [10]. From a historical viewpoint, the term trifocal tensor originated from the seminal studies [11, 36] on the trilinear constraints for three uncalibrated views, although their counterpart for line triplets in three calibrated views [42] appeared much earlier. The $3\times 3\times 3$ tensor has 27 elements, yet the degree of freedom is 18 only in the projective case, which means that these elements should comply with 9 constraints. This naturally arouses the problem of minimal parametrization, which has been widely addressed in the literature [7, 22, 33, 39].

To estimate the trifocal tensor in projective reconstruction requires at least 6 point triplets, for which Quan [34] proposed an effective method. On the contrary, no less than 9 line triplets are required for this estimation, for which the state-of-the-art solver in [21] is still too huge to be practical. Therefore, it is common to use a linear estimation method using 13 or more line correspondences [12], and refine the result through iterative nonlinear optimization. Trifocal tensor estimation in the calibrated case is involved as well, because of the presence of two rotations. A specialized minimal solver is presented in [21] for camera motions with given rotation axis. Very recently, Martyushev [24] characterized the constraints on general calibrated trifocal tensor, which include 99 quintic polynomial equations. Kileel [19] studied the minimal problems for calibrated trifocal variety and reported some numerical results by using the homotopy continuation method. Since the computation is prohibitively slow, people tend to solve the essential matrix arising from two-view geometry instead.

3 Polarimetric Reflectance Under Single View

Polarization arises when an incident light propagates through a surface between two mediums of different refractive indices. Fresnel equations describe an ideal physical model that only considers single bounce surface reflection from directional light. As illustrated in Fig. 2a, the light is thought of as a linear superposition of two independent EM waves: one whose oscillation is in the plane of incidence $\mathbf {\varPi }_{\perp }(\mathbf {n})$ perpendicular to the surface of normal $\mathbf {n}$, one oscillates in the plane $\mathbf {\varPi }_{\parallel }(\mathbf {n})$ parallel to the same surface. As an unpolarized light impinges on the surface, its propagation bifurcates: one branch is immediately reflected off from the surface, the other refracts through the surface. The two wave components share their path, but how they allocate the power upon bifurcation is opposite. Along the light path after bifurcation, one wave component always outpowers the other, and the magnitude of power discrepancy is measured by degree of polarization. In the plane $\mathbf {\varPi }$ where the polarizer is located, the angular distance between the peaks of a wave component along different paths is measured by the relative polarization phase. By conservation of energy and orthogonality, we establish the following:

Proposition 1

At a dielectric surface boundary, any pair of reflected or refracted light inside parallel incident planes is always in phase (i.e. 0 relative polarization phase), and any pair of reflected and refracted light is always out of phase (i.e. $\frac{\pi }{2}$ relative polarization phase) (i.e. out of phase¹).

The phenomena described in Proposition 1 indicates that the relative polarization phase is shared by co-plannar reflections/refractions, as indicated in Fig. 2b. Since incident plane contains the information about both of the surface and the incident light, as opposed to the existing literature that elaborates on the degree of polarization, in the following we investigate the connection between the polarization phase and some important geometrical properties pertaining to view, scene and light.

Fig. 2.

The Fresnel equation explains how an unpolarized incident light becomes polarized through mirror reflection. (a) When reflection and refraction take place under directional light, the polarization phase indicates the orientation of the plane of incidence, and there will be no light traveling outside it. (b) Inside the plane of incidence, coplanar propagations along multiple paths must exhibit identical phase, hence it has to be differentiated by wave magnitude.

Fig. 3.

Polarization of general reflectance over a rough surface can be understood through microfacet configuration. A unique configuration made by the line of sight $\mathbf {v}$ and the incident light $\mathbf {l}$ will only activate the microfacets aligning with the bisector $\mathbf {h}$. (a) Each microfacet acts as a tiny mirror so that its reflection follows Fresnel equation. (b) When light carrying constant power impinges from all directions, the aggregated polarization effect observed can be approximated as if it is measured from a mirror with the same orientation, hence the readings indicate the surface normal.

3.1 Polarization Defined by Directional Light

Our investigation starts with a formulation with directional light. We model the surface using a typical microfaceted setting [41], namely a subset of mirror-like microfacets are selected by the unit vector $\mathbf {h}$ bisecting the line of sight vector $\mathbf {v}$ and light vector $\mathbf {l}$ to produce a specular reflection. The spatially varying reflection depends on the effective visible area $A(\mathbf {h})$ [14] formed by the selected facets according to the microfacet distribution function. As depicted in Fig. 3, specular reflection is solely determined by the direction of the light but not the scene structure. Essentially, the observation is the outcome of a structure defined by $\mathbf {\varPi }_{\perp }(\mathbf {h})$ and $\mathbf {\varPi }_{\parallel }(\mathbf {h})$ whose properties are summarized by Proposition 1. Therefore we arrive at the following:

Proposition 2

Under directional light, the relative polarization phase due to general surface reflection is indicated by the projection of the incident plane formed by $\mathbf {l}$ and $\mathbf {v}$ onto the polarizer.

We can experimentally verify this fact using two observations presented in Fig. 4a, b: when the line of sights tend to be parallel, the relative phase of polarization is in phase and apparently independent of surface orientation, but it can be affected by perspective projection.

Moreover, let $I_{\perp }(\mathbf {h})$ and $I_{\parallel }(\mathbf {h})$ be the power of the two orthogonal wave components confined in $\mathbf {\varPi }_{\perp }(\mathbf {h})$ and $\mathbf {\varPi }_{\parallel }(\mathbf {h})$ respectively, then a polarizer with rotation $\mathbf {w}$ in its own coordinates reads:

$$\begin{aligned} I(\mathbf {w},\mathbf {h}) = A(\mathbf {h})I_{\perp }(\mathbf {h})\cos ^2\theta + A(\mathbf {h})I_{\parallel }(\mathbf {h})\sin ^2\theta \end{aligned}$$

(1)

with $\theta$ denotes the angle made between $\mathbf {w}$ and the projected line from $\mathbf {\varPi }_{\perp }(\mathbf {h})$ to the polarizer. It is worth noting that Eq. 1 is the microfacet version of the expression for the sinusoidal curve that has been widely analyzed in other literatures. For surface reflections, $I(\mathbf {w},\mathbf {h})$ vanishes only when $\mathbf {v}$ and $\mathbf {h}$ make the Brewster’s angle. Hence, the polarizer essentially detects the configuration of $\mathbf {\varPi }_{\parallel }(\mathbf {h})$ and $\mathbf {\varPi }_{\perp }(\mathbf {h})$ for a specific $\mathbf {h}$.

3.2 Polarization Defined by Surface

While how a directional light becomes polarized through reflection depends on its incident angle, under environment light of uniform power, the collective behavior of polarization reflects the surface geometry. For reflectance received from environment map $\varOmega _+$, by Eq. 1 the radiance perceived by polarizer with rotation $\mathbf {w}$ is defined as:

$$\begin{aligned} I(\mathbf {w})&= \int _{\varOmega _+} A(\mathbf {h})I_{\perp }(\mathbf {h})\cos ^2\theta + A(\mathbf {h})I_{\parallel }(\mathbf {h})\sin ^2\theta \,\mathrm {d}\mathbf {h} \nonumber \\&= \int _{-\frac{\pi }{2}}^{\frac{\pi }{2}}\cos ^2\theta \int _{\mathbf {\varPi }(\phi )} A(\mathbf {h})I_{\perp }(\mathbf {h})\mathrm {d}\mathbf {h} + \sin ^2\theta \int _{\mathbf {\varPi }(\phi )} A(\mathbf {h})I_{\parallel }(\mathbf {h})\mathrm {d}\mathbf {h}\mathrm {d}\phi \\&= \int _{-\frac{\pi }{2}}^{\frac{\pi }{2}} F(\phi ,\mathbf {w})\mathrm {d}\phi \nonumber \end{aligned}$$

(2)

where $\mathbf {h} \in \mathbf {\varPi }(\phi )$ lies in a plane that is orthogonal to the image plane $\mathbf {\varPi }$, creating an aggregation of coplanar reflection as described by Proposition 1 and demonstrated in Fig. 3b. Since $F(\phi )$ exhibits an identical structure to Eq. 1, $I(\mathbf {w})$ can be understood as a composition of a set of distinctive sinusoidal curves sharing some specific $\phi$. In other words, $F(\phi ,\mathbf {w}) = I_{\min }(\phi ) + (I_{\max }(\phi ) - I_{\min }(\phi ))\cos (\theta + \phi )$, where $I_{\min }$ and $I_{\max }$ are determined by $\int _{\mathbf {\varPi }(\phi )} A(\mathbf {h})I_{\perp }(\mathbf {h})\mathrm {d}\mathbf {h}$ and $\int _{\mathbf {\varPi }(\phi )} A(\mathbf {h})I_{\parallel }(\mathbf {h})\mathrm {d}\mathbf {h}$. Here evaluating their exact quantities is unnecessary.

If $A(\mathbf {h})$ is derived from a material displaying isotropic reflectance, $\mathbf {v}$ avoids the grazing incidence (i.e. $\mathbf {n}^\intercal \mathbf {v} \gg 0$), then the shadowing effect becomes minor (i.e. equal to 1), and as a result $A(\mathbf {h})$ becomes rotationally invariant about $\mathbf {n}$ (i.e. $A(\mathbf {h}_1) = A(\mathbf {h}_2)$ given that $\mathbf {n}^\intercal \mathbf {h}_1 = \mathbf {n}^\intercal \mathbf {h}_2$). By symmetry about $\phi = 0$ we have $I_{\max }(\phi ) = I_{\max }(-\phi )$ and $I_{\min }(\phi ) = I_{\min }(-\phi )$ under the environment light of uniform power. Furthermore, $F(\phi ,\mathbf {w}) + F(-\phi ,\mathbf {w}) = 2I_{\min }(\phi ) + 2\cos \phi (I_{\max }(\phi ) - I_{\min }(\phi ))\cos \theta$, which is in phase with $F(\phi = 0)$. Therefore, Eq. 2 leads to $I(\mathbf {w}) = C_1(\mathbf {v},\mathbf {n})F(\phi =0,\mathbf {w})$ with $C_1(\mathbf {v},\mathbf {n})$ being some constant.

In practise, $A(\mathbf {h})$ peaks when $\mathbf {h} = \mathbf {n}$. Also, Fresnel equation implies that at grazing incidence the mirror reflection becomes dominant, meaning the light that leads to $\mathbf {h}^\intercal \mathbf {v} \rightarrow 0$ and $\mathbf {h} \rightarrow \mathbf {n}$ contributes the most to the actual reflectance. Therefore, when $\mathbf {v}$ is set at the grazing angle, $I(\mathbf {w}) = C_2(\mathbf {v},\mathbf {n})F(\phi =0,\mathbf {w})$ also serves as a good approximation for Eq. 2. Combining these two scenarios, we summarize the following:

Proposition 3

Under environment light of constant power, the relative polarization phase of general surface reflection is indicated by the projection of the plane formed by $\mathbf {n}$ and $\mathbf {v}$ onto the polarizer.

3.3 Mixed Polarization with Diffusive Reflection

In practise, diffusive reflection due to subsurface scattering is usually observed in tandem with surface reflection. Because refracted light tends to depolarize isotropically as it is scattered by the microstructure underneath the surface, a portion of it has a chance to refract back after several bounces and rejoins the propagation of directly reflected light [3]. This process to generate diffusive reflection can be thought of a byproduct of direct surface reflection by the environment map of constant power $\varOmega _{-}$ covering the lower hemisphere. By Propositions 1 and 3 we derive the following for the observation made in $\varOmega _{+}$:

Proposition 4

The relative phase of general diffusive reflection is determined by the projection of the plane formed by $\mathbf {n}$ and $\mathbf {v}$ onto the polarizer, and it differs in phase from the direct surface reflection by $\frac{\pi }{2}$.

This endorses the finding claimed in [3, 8]. This fact together with Proposition 3 can be experimentally verified and the results are demonstrated in Fig. 4c.

To sum up, under single view the relative polarization phase measured for a specific scene point might be led by two types of phenomena: the specular reflections encoding the incident light or the diffusive reflections encoding the surface normal. It is worth noting that the conclusions made heretofore is independent of the settings for camera. Section 4 shows that by unifying the polarization phase obtained from different views, one can retrieve the relative rotations of the cameras.

Fig. 4.

The relative phase measured under single view with various light-view-geometry configuration. It can be seen that specular reflection is dependent only on view and light, while diffusive reflection depends on the geometry of the scene. (a)(d) orthographic specular reflection displays in phase polarization. (b)(e) perspective specular reflection displays slightly out-of-phase polarization. (c)(f) polarization phase shift due to diffusive reflections indicates the geometry of the scene.

4 Polarimetric Geometry Under Three Views

The relative pose between the camera and a scene point is regulated by two types of planes: (1) those formed by $\mathbf {v}$ and $\mathbf {l}$ (Sect. 3.1) and (2) those formed by $\mathbf {v}$ and $\mathbf {n}$ (Sects. 3.2 and 3.3). Accordingly, in a multi-view setup, for each point there exist two clusters of planes, one belongs a type. Inside each cluster, the orientation of the plane in the camera’s local coordinates is represented by the detected relative polarization phase. We show that, using a static scene under static illumination, the polarization phases captured from three distinctive views avail us the relative pose of a the cameras.

4.1 Formulation

We setup a system of cameras indexed by j with optical center denoted by $\mathbf {o}_j$. Their poses are described by rotation matrices $\mathbf {R}_j$ together with the corresponding translation vectors $\mathbf {t}_j$. Each camera pose has six degrees of freedom, with three of them parameterizing $\mathbf {R}$. As indicated in Fig. 5, Let $S_i$ denote a scene point indexed by i. From Sect. 3 we know that linking each point $S_i$ to camera j is a vector $\mathbf {h}_{i,j}$ that represents the projection of $\mathbf {h}$ onto the image plane $\mathbf {\varPi }$ centered at $\mathbf {o}_j$. $\mathbf {h}$ is obtained by fitting $\mathbf {w}$ to Eq. 1, which does not involve projection. Let $\mathbf {n}_{ij}$ denote the normal of the induced plane of incidence $\mathbf {\varPi }_{ij}$ and $\mathbf {v}_{ij}$ the line of the sight, and according to the reflectance type we either have $\mathbf {n}_{ij} = \mathbf {n}_{i} \times \mathbf {v}_{ij}$ or $\mathbf {n}_{ij} = \mathbf {l} \times \mathbf {v}_{ij}$. Moreover, there exists a matrix, $\mathbf {N}_i$ for scene point $S_i$ as:

$$\begin{aligned} \mathbf {N}_i = \begin{bmatrix} \mathbf {n}_{i,1}&\mathbf {R}_2\mathbf {n}_{i,2} \ldots \mathbf {R}_j\mathbf {n}_{i,j} \ldots \end{bmatrix} \end{aligned}$$

(3)

where we let $\mathbf {R}_1 = \mathbf {I}$. Correspondingly, another matrix , $\mathbf {N}_l$, can also be constructed for directional light $\mathbf {l}$. By definition we have:

$$\begin{aligned} \mathbf {N}_i = [\mathbf {n}_i]_{\times } \begin{bmatrix} \mathbf {v}_{i,1}&\mathbf {R}_2\mathbf {v}_{i,2} \ldots \mathbf {R}_j\mathbf {v}_{i,j} \ldots \end{bmatrix} \end{aligned}$$

(4)

and

$$\begin{aligned} \mathbf {N}_l = [\mathbf {l}]_{\times } \begin{bmatrix} \mathbf {v}_{i(1),1}&\mathbf {R}_2\mathbf {v}_{i(2),2} \ldots \mathbf {R}_j\mathbf {v}_{i(j),j} \ldots \end{bmatrix} \end{aligned}$$

(5)

where i(j) indexes the position of the floating specularity observed from view j, and $[\cdot ]_{\times }$ is the matrix representation for cross product, whose rank is always 2. Therefore, the rank of both $\mathbf {N}_i$ and $\mathbf {N}_l$ is also 2.

Equations 4 and 5 indicate that, the aforementioned cluster of plane $\{\mathbf {\varPi }\}_{ij}$ are two pencils of planes: one has axis aligned with $\mathbf {n}_i$, and the other has axis passing through $\mathbf {l}$. The difference is that $N_i$ represents a pencil of planes whose members physically coincide with $\mathbf {\varPi }_{ij}$, while $N(\mathbf {l})$ indicates a pencil of planes that contains translated $\mathbf {\varPi }_{ij}$, as depicted in Fig. 5. In both cases the rank-2 constraints hold, hence our derivation can be summarized as follows:

Proposition 5

In a multi-view system with one dominant directional light, the polarization displayed by a scene point may induce one of two pencils of planes, one has its axis aligned with the propagation of the directional light, and the other has its axis passing through the surface normal.

Since $[\mathbf {l}]\times$ denotes light direction, $[\mathbf {n}_i]\times$ represents scene structure, and $\mathbf {v}_{ij}$ is represented pixel location, Eqs. 4 and 5 effectively decouple camera translation from the camera rotation and camera model. So, polarimetric information is highly useful for rotation estimation.

Fig. 5.

Construction for three-view geometry. The structure represented by the two figures are identical given that the incident light are parallel, but physically incidence planes induced by light are not necessary intersect on the single line

4.2 From Three-View Polarization to Camera Rotation

For camera pose estimation, the rank-2 constraint imposed on $\mathbf {N}_i$ and $\mathbf {N}_l$ is critical. It allows us to set up a theoretical formulation for the corresponding minimal system and then extend it into a relaxed least square setup. More importantly, leveraging both $\mathbf {N}_l$ and $\mathbf {N}_l$ can resolve ambiguity caused by mixed polarizations effectively.

An Extended Least Square Solver. In the minimal case $\mathbf {N}_i$ and $\mathbf {N}_l$ are two 3-by-3 matrices (i.e. $j\in \{1,2,3\}$) to be determined through $\mathbf {R}_{2}$ and $\mathbf {R}_{3}$, which in our formulation are expressed by two unit-norm 4-by-1 vectors $\mathbf {q}_2$ and $\mathbf {q}_3$ in quaternions respectively. Each vector contains three unknowns, so six points to form six pencils of planes of unique axes can completely determine $\mathbf {R}_{2}$ and $\mathbf {R}_{3}$. In particular, we establish a system of six equations of 4-th order polynomials: $\det \mathbf {N}_i = 0$ with an additional constraint $\det \mathbf {N}_l = 0$ ($1\le i\le 6$) to resolve the $\frac{\pi }{2}$ phase ambiguity caused by mixed polarization.

As mentioned, directly solving the minimal problem using 6 points is computationally challenging. A simple instance we created for off-line evaluation shows that the correct solution is buried among 4252 candidates in the complex domain. Aside from applying additional assumptions [21], for our setup we propose to directly apply the non-linear least square solver that takes few more points. We believe this is feasible for two reasons: (1) we only need a sparse set of robust correspondences to define camera pose; (2) polarization measurements are susceptible to noise, relaxed formulation should strengthen our estimation.

Resolving Mixed Polarization. In the presence of specularity, $\frac{\pi }{2}$-ambiguity due to mixed polarizations observed from three views may result in each $\mathbf {n}_{ij}$ having 8 possible interpretations. This combination makes even a minimal system prohibitively large to solve ($6^8 = 1679616$). Ordering the strength of specularity will reduce the number of combinations ($6^4 = 1296$), but this reduced set is still far from being feasible. On the other hand, under general reflectance with complex scene structure, specularities often appear but distribute sparsely in space. In other words, if majority of point correspondences diffusive-diffusive-diffusive, few specular-specular-specular may be excluded through intensity profiling. However, there is a chance that ideal diffusive correspondences being mistaken as specular ones are excluded. In our case we can construct a hypothetical $\mathbf {N}_l$ using the estimated result to verify the result. If the estimation is accurate, the resulting matrix should also be rank-deficient. Such consistency motivates us to design a solution consisting of two subroutines with one to address the $\frac{\pi }{2}$ ambiguity caused by specularities produced by a directional light:

 

selecting diffusion-only correspondences :

Excluding the correspondences involving plausible specularities by intensity profiling (i.e. the brightest pixels in the scene). Applying the remaining correspondences to create instances of $\mathbf {N}_i$, and solve for $\min (\sum _i \det \mathbf {N}_i)^2$.

disambiguating using specularities :

Including the plausible specularities to construct a hypothetical $\mathbf {N}_l$. If the construction is valid, it has to be rank deficient. Otherwise, flip the input by $\frac{\pi }{2}$ to detect a minimum determinant. This can be achieved after 3 attempts. Then make it a input to the estimator.

The above procedure proceeds iteratively until no flipping can help improve the results.

Essentially, $\mathbf {N}_l$ serves as a robust constraint to cross-validate the consistency over all observations. This design draws strong analogy to the RANSAC-based methods for feature correspondences. Designing a better framework integrating both is left as part of our future work.

4.3 Illumination, Structure and Camera Calibration

Knowledge about $\mathbf {N}_i$ and $\mathbf {N}_l$ can be further applied to retrieve the lines carry surface normal, the direction of the light and the camera’s focal length. Under orthographic or weak perspective projections, Eqs. 4 and 5 can be reduced to:

$$\begin{aligned} N_i = [\mathbf {n}_i]_{\times } \begin{bmatrix} \mathbf {I}&\mathbf {R}_2 \ldots \mathbf {R}_j \ldots \end{bmatrix}\mathbf {v} \end{aligned}$$

(6)

and

$$\begin{aligned} N_l = [\mathbf {l}]_{\times } \begin{bmatrix} \mathbf {I}&\mathbf {R}_2 \ldots \mathbf {R}_j \ldots \end{bmatrix}\mathbf {v} \end{aligned}$$

(7)

respectively, where under orthographic projection $\mathbf {v} = [0,0,1]$ and under weak perspective projection $|\mathbf {v}|$ is assumed to be an unknown constant (i.e. independent of the actual scene structure). Orthographic projection only considers rotation, and it is a common assumption made for normal estimation in the existing literatures. Weak perspective projections, on the other hand, additionally consider camera translation over a unknown spherical surface. In both situations one can recover surface normal according to Eq. 6, and light direction according to Eq. 7. Perspective projection with focal length $f_j$, $\mathbf {v}_{ij} = (x_{i},y_{i},f_j)$ and the optical axis passes through the square image center yield a system of quadratic equation in terms of $\mathbf {n}_i$ and $f_j$ by Eq. 4.

4.4 Comparison with Trifocal Tensor

With $\mathbf {P}_{j} = [\mathbf {P}_{j,1:3}|\mathbf {P}_{j,4}]: S \rightarrow s_{j}$ being the projection operator projecting S onto the image plane $\mathbf {\varPi }_{j}$, we are able to link the formulation presented in Sect. 4.1 to trifocal tensor [10]:

$$\begin{aligned} \mathbf {M} = \begin{bmatrix} \mathbf {P}_{1,1:3}^{\intercal }\mathbf {h}_1&\mathbf {P}_{2,1:3}^{\intercal }\mathbf {h}_2&\mathbf {P}_{3,1:3}^{\intercal }\mathbf {h}_3 \\ \mathbf {P}_{1,4}^{\intercal }\mathbf {h}_1&\mathbf {P}_{2,4}^{\intercal }\mathbf {h}_2&\mathbf {P}_{3,4}^{\intercal }\mathbf {h}_3 \end{bmatrix} \end{aligned}$$

(8)

where $\mathbf {h}_j$ is the line projected onto the image planes $\mathbf {\varPi }_j$. M is a 4-by-3 matrix and $rank(M) = 2$. Equations 4, 5 and 8 display similar algebraic properties and exhibit the following connections: (1) $\mathbf {h}_{i,j}$ arises naturally from polarization, so line correspondence is achieved without a line detector marking points along a visible line for correspondence. (2) $\mathbf {N}_i$ in Eq. 4 occupies the first three rows of $\mathbf {M}$ subject to linear scale, so any algorithms designed to address trifocal tensor can be tailored for polarization. (3) The fourth row of the trifocal tensor encodes the camera translation. Therefore, we see that the relative polarization phase essentially serves as a useful cue for camera rotations.

5 Experiments

In order to verify our theory under the proper illumination setup, we require at most one strong and directional to be present. In our case this can be the light mounted on the ceiling. A linear polarizer is embedded inside a motorized rotator, and it is mounted in front of a grey scale camera, which we calibrate according to [45]. In our experiment, we use 11 distinctive exposures to obtain the HDR images for each scene to reduce saturation. Also, for each exposure we average the result multiple times in order to reduce the thermal noise of the device. We perform verifications and pose estimations in separate experiments. In each scene, checkerboards are also included to obtain the ground truth.

5.1 Verification

We use two separate scene to verify the existence of rank deficient matrices, $\mathbf {N}_i$ and $\mathbf {N}_l$, respectively. We use “dice” to setup the scene for diffusive reflections and “ball” to produce specular reflections. Specifically, in “dice” we manually select 20 anchor correspondences and then populate the correspondences using their neighboring pixels. We evaluate the statistics of the singular values of the obtained matrices. From Fig. 6 we observe that the smallest singular value maintain to be significantly lower than the largest singular value, indicating that the matrices indeed tend to be rank deficient in practise.

For specular settings, we select 30 samples from the brightest pixels and construct $\mathbf {N}_l$ through random matching. The statistics of singular values show that it is also highly rank deficient because the smallest singular value on average almost vanishes compared with the largest singular value (Fig. 7). Also, in both scenarios the intensity variations of good correspondences display clean sinusoidal curves with apparent phase shift, and their magnitudes do not affect the structure of our proposed structures.

Fig. 6.

Verification experiment for diffusive reflections. (d): the statistics of the singular values obtained from the sampled instances. (e): a plot for intensity variation of a good correspondence.

Fig. 7.

Verification experiment for specular reflections. (d): the statistics of the singular values obtained from the sampled instances. (e): a plot for intensity variation of a good correspondence.

5.2 Estimation

We set up a real-world scene to showcase our solution, and its estimation results are visualized in Fig. 8. Our goal is to estimate the rotations, and the due to the space limit our configuration leads to orthographic projection. The resulted rotation matrices are evaluated relative to its ground truth. Here $R_{12}$ indicates the relative rotation from view 2 to view 1: $R_{12} = (0.9977,0.9915,0.9892)$, $R_{12} = (0.9855,0.9797,0.9652)$ which are intuitively reasonable.

Fig. 8.

An example for estimating the camera pose using polarimetric readings.

The estimation accuracy are mainly degraded by two factors: (1) the measurement noise that are commonly observed for polarization measurements, which occurs often from diffusive reflections and cast shadows; (2) the correspondence might not accurate. In the experiment we also manually include some plausible correspondences inside the textureless region. Since the synergy of these two factors amplifies our estimation error, an effective solution to this issue is under our investigation.

6 Conclusions and Future Work

In conclusion, in this paper we establish the theoretical connection between polarization and three-view geometry, which leads to an example of polarization-enabled estimation on camera poses. In particular, guided by the microfacet theory and the classical Fresnel equations, we experimentally verify the ubiquitous existence of the two types of pencils of planes derived from polarization phase shift, where one is induced by the direct surface reflections and the other by the diffusive reflections due to subsurface scattering. Our formulation shows that a rotatable linear polarizer can extract the relative rotation of a camera from its translation. Also, using pencil of planes induced by light, the specular correspondences cross-validate the estimation obtained from diffusive correspondences with fixed number of steps, which we consider an effective strategy to resolve ambiguities caused by mixed polarizations. Our experiment on real world scene validates our theory and produce desirable results.

However, it is not hard to see that our experiment is still preliminary. Because polarization measurements are vulnerable to noises, whose effect amplifies under uncontrolled illumination. In particular, polarization by diffusive reflections delivers less stable observations than specular reflections do due to the thermal noise of the device. On the other hand, however, diffusive reflections due to subsurface scattering usually carry the dense features for traditional stereo correspondences. These features are also the key reasons that RANSAC-based approaches are resilient to noise. Since our strategy for disambiguation of mixed polarization described in Sect. 4.2 operates in a similar manner, it is reasonable to put both parts into a unified framework. Comparing with fusing polarimetric information structure reconstruction [8], our work showcase that polarization can be directly used to extract some underneath geometric properties about the camera and the scene, which also draws certain analogies to the work of traditional setup [20]. Therefore, exploring the geometric properties embedded inside polarization and integrating them into the traditional framework will be a part of our future work.