Impact of Privacy on Free Online Service Markets

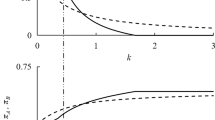
Abstract

The emerging marketplace for online free services in which service providers (SPs) earn revenue from using consumer data in direct and indirect ways has led to significant privacy concerns. This begs understanding of the following question: can the marketplace sustain multiple SPs that offer privacy differentiated free services? This paper studies the impact of privacy on free online service markets by augmenting the classical Hotelling model for market segmentation analysis. A parametrized game-theoretic model is proposed which captures: (i) the fact that for the free service market, consumers value service not in monetized terms but by the quality of service (QoS); (ii) the differentiator of services is not product price but the privacy risk advertised by an SP; and (iii) consumer’s heterogeneous privacy preference for SPs. For the two-SP problem with uniformly distributed consumer privacy preference and linear SP profit function, the results suggest that: (i) when consumers place a higher value on privacy, it leads to a larger market share for the SP providing untargeted services and a “softened” competition between SPs; (ii) SPs offering high privacy risk services are sustainable only if they offer sufficiently high QoS; and (iii) SPs that are capable of differentiating on services that do not directly use consumer data gain larger market share. Similar results are observed when the consumer’s privacy preference is modeled as a truncated Gaussian distribution.

Appendices

Appendix

A Proof of Theorem 1

We prove by contradiction. Suppose that both SPs offer the same privacy risk $\tilde{\varepsilon }$. Without loss of generality, we assume $p_1\le p_2$. We start at the third stage wherein each consumer chooses the SP which maximizes its utility (5). Since $\varepsilon ^*_1=\varepsilon ^*_2=\tilde{\varepsilon }$, every consumer will choose the SP that offers the highest QoS. At the second stage, given the privacy risk strategy $\varepsilon ^*_1=\varepsilon ^*_2=\tilde{\varepsilon }$ and the equilibrium strategy in the third stage, each SP determines its QoS offering by solving (10). Finally, we show that $SP_2$ will be better off if it deviates from $\tilde{\varepsilon }$ unilaterally. By Assumption 3, each SP has equal share of the market if $v_1=v_2$ and $\varepsilon _1=\varepsilon _2$. The profit of $SP_i$ can be written as

$$\begin{aligned} \pi _i&= \left\{ \begin{array}{ll} r\varepsilon _i+p_i-c(v_i+\lambda \varepsilon _i) &{} \hbox {if } v_i>v_{-i} \\ \frac{r\varepsilon _i+p_i-c(v_i+\lambda \varepsilon _i)}{2} &{} \hbox {if } v_i=v_{-i} \\ 0 &{} \hbox {if } v_i<v_{-i} \end{array} \right. . \end{aligned}$$

(25)

As argued in Sect. 2.1, we assume that the net profit from using consumers’ private data is non-negative $R_P(\varepsilon _i)-C_P(\varepsilon _i)>0$. Thus, $(r\,-\,c\lambda )\varepsilon _i>0$ $\forall \varepsilon _i\in [0, \bar{\varepsilon }]$, which indicates $r-c\lambda >0$. Since every consumer will choose the SP that offers the highest QoS, each SP’s best response strategy with respect to its competitor is to increase $v_i$ until one of the SPs realizes it is not profitable to increase QoS anymore. Therefore, by (25), both SPs will increase $v_i$ until $R(\varepsilon _i)-C(v_i, \varepsilon _i)=0$ for one of the SPs. Since we assume $p_1\le p_2$, we have the following two cases:

Case 1: $p_1=p_2=p$. In this case, given $\varepsilon ^*_1=\varepsilon ^*_2=\tilde{\varepsilon }$, each SP will increase its QoS to beat its competitor until $R(\varepsilon _i)-C(v_i, \varepsilon _i)=r\tilde{\varepsilon }+p-c(v_i+\lambda \tilde{\varepsilon })=0$. As a result, both SPs’ equilibrium strategies at this stage are given by

$$\begin{aligned} v^*_1=v^*_2=\frac{(r-c\lambda )\tilde{\varepsilon }+p}{c}. \end{aligned}$$

(26)

At the first stage, the SPs determine their privacy risks based on the equilibrium strategies in the second and the third stages. Given the equilibrium strategies in the second stage (26), both SPs have zero profit. Since we assume $\varepsilon _1\le \varepsilon _2$, $SP_1$ can only reduce its privacy risk from $\tilde{\varepsilon }$ and $SP_2$ can only increase from it. We now prove that it is a non-profitable deviation for $SP_1$ to decrease its privacy risk to $\tilde{\varepsilon }_1$ unilaterally. Since $SP_1$’s QoS strategy is given by $v^*_1=\frac{(r-c\lambda )\tilde{\varepsilon }+p}{c}$, its profit is given by $R(\tilde{\varepsilon }_1)-C(v^*_1, \tilde{\varepsilon }_1)=r\tilde{\varepsilon }_1+p-c(v^*_1+\lambda \tilde{\varepsilon }_1)=(r-c\lambda )(\tilde{\varepsilon }_1-\tilde{\varepsilon })<0.$ Thus, $SP_1$ does not have incentives to deviate from playing $\tilde{\varepsilon }$ unilaterally. On the other hand, if $SP_2$ increases its privacy risk from $\tilde{\varepsilon }$ to $\tilde{\varepsilon }_2$ unilaterally, its profit is given by $R(\tilde{\varepsilon }_2)-C(v^*_2, \tilde{\varepsilon }_2)=r\tilde{\varepsilon }_2+p-c(v^*_2+\lambda \tilde{\varepsilon }_2)=(r-c\lambda )(\tilde{\varepsilon }_2-\tilde{\varepsilon })>0.$ Therefore, $SP_2$ is better off by changing from $\tilde{\varepsilon }$ to $\tilde{\varepsilon }_2$ unilaterally. Thus, there is no SPNE such that both SPs offer the same privacy risk when $p_1=p_2$.

Case 2: $p_1<p_2$. In this case, since $p_1<p_2$, both SPs will keep increasing its QoS until $SP_1$ has zero profit. Thus, by solving $R(\tilde{\varepsilon })-C(v_1, \tilde{\varepsilon })=0$, $SP_1$ will play $v^*_1=\frac{(r-c\lambda )\tilde{\varepsilon }+p_1}{c}$ at the equilibrium. On the other hand, $SP_2$ will offer an QoS slightly higher than $v^*_1$ and captures the entire market. At the first stage, given the equilibrium strategy of the second stage described above, both SPs choose their privacy risk offerings. We now prove that it is a non-profitable deviation for $SP_1$ to decrease its privacy risk to $\tilde{\varepsilon }_1$ unilaterally. Substitute $v^*_1=\frac{(r-c\lambda )\tilde{\varepsilon }+p_1}{c}$ to (25), we have $\pi _1 =(r-c\lambda )(\tilde{\varepsilon }_1-\tilde{\varepsilon })<0.$ Thus, $SP_1$ does not have incentives to deviate from playing $\tilde{\varepsilon }$ unilaterally. On the other hand, if $SP_2$ increases its privacy risk from $\tilde{\varepsilon }$ to $\tilde{\varepsilon }_2$ unilaterally, its profit is given by

$$\begin{aligned} \pi _2&=(r-c\lambda )(\tilde{\varepsilon }_2-\tilde{\varepsilon })+p_2-p_1=(r-c\lambda )(\tilde{\varepsilon }_2-\tilde{\varepsilon })+R(\tilde{\varepsilon })-C(v^*_2, \tilde{\varepsilon })\\\nonumber&>R(\tilde{\varepsilon })-C(v^*_2, \tilde{\varepsilon }). \end{aligned}$$

Thus, $SP_2$ has incentives to deviate from offering the same privacy risk. Therefore, playing $\varepsilon ^*_1=\varepsilon ^*_2=\tilde{\varepsilon }$ is not an SPNE when $p_1<p_2$.

B Proof of Theorem 2

Starting form the last stage in which consumers choose different SPs, we use backward induction to find the SPNE of the sequential game. In the last stage, each consumer located at $x\in [0,1]$ chooses an SP which maximizes its utility function (3). By (6) and the assumption that consumers’ privacy risk tolerances are uniformly distributed, the indifference threshold $x_\tau$ is given by

$$\begin{aligned} x_\tau =\frac{v_1-v_2+\frac{t(\varepsilon ^2_2-\varepsilon _1^2)}{\bar{\varepsilon }}}{t(\varepsilon _2-\varepsilon _1)}=n_1(v_1;\varepsilon _1;v_2;\varepsilon _2). \end{aligned}$$

(27)

At the second stage, the optimal strategy of each SP is determined by the solution of (10). For fixed privacy risk guarantees $\varepsilon _2$ and $\varepsilon _1$, the objective function of $SP_i, i\in \{1,2\}$ in this stage, i.e., $\pi _i(v_i;\varepsilon _i; v_{-i}; \varepsilon _{-i})$, is a concave function with respect to its own strategy $v_i$. Furthermore, the feasible set of $SP_i$’s strategy is a convex set ($v_i\in [0,+\infty ]$). Thus, the non-cooperative subgame between $SP_2$ and $SP_1$ in this stage can be considered as a two-player concave game. By Theorem 1 and 2 in [23], we can establish

Proposition 1

For fixed privacy risk strategies, there exists a unique Nash equilibrium in the game between $SP_2$ and $SP_1$ at the second stage.

Proof

To compute the equilibrium strategy of the second stage, we first substitute (11), (12), and (27) into (8) and (7). Then, we apply the first order condition to SPs’ profit functions and solve the simultaneous equations given by $\frac{\partial \pi _i(v_i;\varepsilon _i; v_{-i}; \varepsilon _{-i})}{\partial v_i}=0 \quad \forall i\in \{1,2\}.$

For given privacy guarantees $\varepsilon _1$ and $\varepsilon _2$, solving the simultaneous linear equations above yields the unique equilibrium strategy

$$\begin{aligned} v^*_1 =\frac{2(r\varepsilon _1+p_1)+r\varepsilon _2+p_2}{3c} +\frac{t(1+x_1)\varepsilon _1-\lambda (\varepsilon _2+2\varepsilon _1)-t(1+x_2)\varepsilon _2}{3},\end{aligned}$$

(28)

$$\begin{aligned} v^*_2 =\frac{2(r\varepsilon _2+p_2)+r\varepsilon _1+p_1}{3c} +\frac{t(2-x_1)\varepsilon _1-\lambda (2\varepsilon _2+\varepsilon _1)-t(2-x_2)\varepsilon _2}{3}. \end{aligned}$$

(29)

At the first stage, SPs determine their optimal privacy risks by considering the QoS of each SP and the market segmentation computed in previous stages as functions of privacy risks offered by SPs. Substituting (29) and (28) into (8) and (7) and apply the first order condition to SPs’ profit functions yields (14) and (16). Substitute (14) and (16) to (29) and (28) yields (15) and (17).

Next, we prove the sufficient condition for the existence of the above SPNE. First of all, the model parameters must sustain a competitive market environment. Thus, in the equilibrium, each SP must have non-zero market share. This indicates the parameters must satisfy $0\le x^*_\tau =\frac{v^*_1-v^*_2+t(x^*_2\varepsilon ^*_2-x^*_1\varepsilon ^*_1)}{t(\varepsilon ^*_2-\varepsilon ^*_1)} \le 1$. Substitute (14), (15), (16), and (17) into the above inequality, we have (18). Furthermore, in the SPNE, the QoS of each SP must be non-negative (QoS feasibility) and the privacy risk guarantees must be bounded between 0 and $\bar{\varepsilon }$ (privacy risk feasibility). By the model assumption in Sect. 2.1, we have $\varepsilon _1\le \varepsilon _2$. Thus, we only requires $\varepsilon _2\le \bar{\varepsilon }$ and $\varepsilon _1\ge 0$. Substitute (14) and (16) into the two inequalities above yields (19). Let $x^*_i=\frac{\varepsilon ^*_i}{\bar{\varepsilon }}$ denote the normalized privacy risk of each SP in the SPNE. The SPNE strategies must satisfy the complete market coverage condition given by $u_i(x)=v^*_i-t(x-x^*_i)\varepsilon ^*_i\ge 0, \forall x\in [0,1]$ for at least one SP.

Substituting (19) into (17), we have $v^*_2-v^*_1=\frac{3\bar{\varepsilon }}{4}\alpha -\frac{p_2-p_1}{3c}\ge \frac{3t\bar{\varepsilon }}{16}+\frac{2(p_2-p_1)}{3c}>0$, thus we only need $v_1\ge 0$ for QoS feasibility. Furthermore, the Hotelling model feasibility condition implies $v^*_1-tx^*_1\varepsilon ^*_1\ge v^*_2-tx^*_2\varepsilon ^*_2$. Since $u_i(x)$ is an increasing function of x, complete market coverage condition can be simplified to $u_1(0)\ge 0$. As a result, the QoS feasibility condition and the complete market coverage condition can be simplified to $v^*_1-tx^*_1\varepsilon ^*_1\ge 0$. Therefore, the sufficient condition for the existence of SPNE is given by: (i) $0 \le \frac{v^*_1-v^*_2+t(x^*_2\varepsilon ^*_2 -x^*_1\varepsilon ^*_1)}{t(\varepsilon ^*_2-\varepsilon ^*_1)}\le 1$; (ii) $0 \le \varepsilon ^*_1, \varepsilon ^*_2 \le \bar{\varepsilon }$; (iii) $v^*_1-tx^*_1\varepsilon ^*_1\ge 0$. Solving the above three inequalities yield (18)–(20). The equilibrium market share and profits of the SPs are obtained by substituting (14)–(17) into (6)–(8).