Abstract
Even though players in a game optimize their goals by playing an equilibrium, the perceived payoff per round may (and in most cases will) deviate from the expected average payoff. For the example of loss minimization, an undercut of the expected loss is unproblematic, while suffering more than the expected loss may disappoint the player and lead it to believe that the played strategy is not optimal. In the worst case, this may subsequently cause deviations towards seemingly better strategies, even though the equilibrium cannot be improved in general. Such deviations from the utility maximization principle are subject of bounded rationality research, and this work is a step towards more accurate game theoretic models that include disappointment aversion as an additional incentive. This incentive necessarily creates discontinuities in the payoff functionals, so that Nash’s classical equilibrium theorem is no longer applicable. For games with disappointment aversion (defined in this work) the existence of equilibria can nonetheless be shown, i.e., we are able to find Nash equilibria that comply with disappointment aversion.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
A correspondence
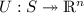 has closed values, if all \(U(\varvec{\mu })\) \(\varvec{\mu } \in S\) are closed subsets of
has closed values, if all \(U(\varvec{\mu })\) \(\varvec{\mu } \in S\) are closed subsets of 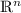 .
.
References
Al-Shaer, E., Duan, Q., Jafarian, J.H.: Random host mutation for moving target defense. In: Keromytis, A.D., Di Pietro, R. (eds.) SecureComm 2012. LNICSSITE, vol. 106, pp. 310–327. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36883-7_19
Alpcan, T., Başar, T.: Network Security: A Decision and Game Theoretic Approach. Cambridge University Press, Cambridge (2010)
Balder, E.J.: An equilibrium closure result for discontinuous games. Econ. Theory 48(1), 47–65 (2010)
Bell, D.E.: Disappointment in decision making under uncertainty. Oper. Res. 33(1), 1–27 (1985)
Chauveau, T., Nalpas, N.: A theory of disappointment (2005)
Crandall, J.W.: Towards minimizing disappointment in repeated games. J. Artif. Int. Res. 49(1), 111–142 (2014)
Glicksberg, I.L.: A further generalization of the kakutani fixed point theorem, with application to nash equilibrium points. Proc. Am. Math. Soc. 3, 170–174 (1952)
Inman, J.J., Dyer, J.S., Jia, J.: A generalized utility model of disappointment and regret effects on post-choice valuation. Mark. Sci. 16(2), 97–111 (1997)
Kahneman, D., Tversky, A.: Prospect theory: an analysis of decision under risk. Econometrica 47, 263–291 (1979)
Lozovanu, D., Solomon, D., Zelikovsky, A.: Multiobjective games and determining pareto-nash equilibria. Buletinul Academiei de Stiinte a Republicii Moldova Matematica 3(49), 115–122 (2005)
Maskin, E., Dasgupta, P.: The existence of equilibrium in discontinuous economic games, part i (theory). Rev. Econ. Stud. 53(1), 1–26 (1986). Reprinted in K. Binmore and P. Dasgupta (eds.), Economic Organizations as Games, Oxford: Basil Blackwell, 1986, pp. 48–82
Rass, S.: On game-theoretic network security provisioning. Springer J. Netw. Syst. Manag. 21(1), 47–64 (2013)
Rass, S., König, S., Schauer, S.: Defending against advanced persistent threats using game-theory. PLoS One 12(1), e0168675 (2017)
Rass, S., König, S., Schauer, S.: On the cost of game playing: how to control the expenses in mixed strategies. In: Rass, S., An, B., Kiekintveld, C., Fang, F., Schauer, S. (eds.) GameSec 2017. LNCS, vol. 10575, pp. 494–505. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68711-7_26
Simon, L.K., Zame, W.R.: Discontinuous games and endogenous sharing rules. Econometrica 58(4), 861–872 (1990)
Sion, M., Wolfe, P.: On a Game without a Value, pp. 299–306. Princeton University Press, Princeton (1957)
Voorneveld, M.: Pareto-optimal security strategies as minimax strategies of a standard matrix game. J. Optim. Theory Appl. 102(1), 203–210 (1999)
Zhu, Q., Rass, S.: On multi-phase and multi-stage game-theoretic modeling of advanced persistent threats. IEEE Access 6(1), 13958–13971 (2018)
Acknowledgment
This work was done in the context of the project “Cross Sectoral Risk Management for Object Protection of Critical Infrastructures (CERBERUS)”, supported by the Austrian Research Promotion Agency under grant no. 854766. We thank the anonymous reviewers for their valuable suggestions that helped to improve this work.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Wachter, J., Rass, S., König, S., Schauer, S. (2018). Disappointment-Aversion in Security Games. In: Bushnell, L., Poovendran, R., Başar, T. (eds) Decision and Game Theory for Security. GameSec 2018. Lecture Notes in Computer Science(), vol 11199. Springer, Cham. https://doi.org/10.1007/978-3-030-01554-1_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-01554-1_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-01553-4
Online ISBN: 978-3-030-01554-1
eBook Packages: Computer ScienceComputer Science (R0)





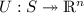 has closed values, if all
has closed values, if all 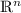 .
.