Random Number Generators Can Be Fooled to Behave Badly

Abstract

In this paper, we extend the work on purely mathematical Trojan horses initially presented in [15]. This kind of mechanism affects the statistical properties of an infected random number generator (RNG) by making it very sensitive to input entropy. Thereby, when inputs have the correct distribution the Trojan has no effect, but when the distribution becomes biased the Trojan worsens it. Besides its obvious malicious usage, this mechanism can also be applied to devise lightweight health tests for RNGs. Currently, RNG designs are required to implement an early detection mechanism for entropy failure, and this class of Trojan horses is perfect for this job.

1 Introduction

In [15] the authors propose an interesting mechanism that blurs the line between what constitutes a Trojan horse and what does not. To detect their mechanism, a program needs to somehow differentiate between a naturally unstable random number generator (RNG) and artificially unstable one (obtained by means of certain mathematical transformations). To our knowledge, [15] is the only previous work that discuses this topic.

More precisely, in [15] a digital filter is described. Usually, digital filters are applied to RNGs to correct biases¹, but this filter has an opposite purpose. When applied to a stream of unbiased bits the filter is benign. On the other hand, if applied to a stream of biased bits the filter amplifies their bias. Thereby, making the RNG worse.

In this paper we extend the filter from [15]², provide a new class of filters and discuss some new possible applications. The main application we propose for these filters is RNG testing (e.g., boosting health tests implemented in a RNG). Recent standards [11, 13] require a RNG to detect failures and one such method for early detection can be to apply an amplifier and then do some lightweight testing³. Based on the results obtained in our paper, we provide concrete examples of how to detect such failures in Sect. 5.1 and Appendix A.

Due to recent events [4, 6, 7, 12] RNGs have been under a lot of scrutiny. Thus, wondering what kind of mechanisms can be implemented by a malicious third party in order to weaken or destabilize a system becomes natural. Amplifying filters provide a novel example of how one can achieve this. Based on the failure detection mechanisms proposed in Sect. 5.1, we show, for example, how a manufacturer can manipulate the architecture to become malicious.

Structure of the paper. Notations and definitions are presented in Sect. 2. The core of the paper consists of Sects. 3 and 4 and contains two classes of filters. Applications are given in Sect. 5. We conclude in Sect. 6. Experimental results are presented in Appendix A.

2 Preliminaries

Throughout the paper, we consider binary strings of length n composed of independent and identically distributed (i.i.d.) bits generated by a RNG. By $0^n$ and $1^n$ we understand the all zero and the all one strings. Also, for figures we use the standard representation of the x-axis and y-axis.

Let $0 \le \varepsilon \le \frac{1}{2}$ be a real number and b a random bit. Then, without loss of generality, we denote the probability of $b=0$ by $P_0 = \frac{1}{2}-\varepsilon$ and of $b=1$ by $P_1 = \frac{1}{2}+\varepsilon$. We will refer to $\varepsilon$ as bias. The complement rule states that $P_1 = 1 - P_0$. Let P(a) be the probability of a random string being a. Then for any $A \subseteq \mathbb {Z}_2^n$ we denote by $P(A) = \sum _{a \in A} P(a)$.

Let u be a binary string and $A \subseteq \mathbb {Z}_2^n$. Then w(u) denotes the hamming weight of u and w(A) the set $\{w(a) \mid a \in A\}$. Note that since we are working with i.i.d. bits, for any $u, v \in \mathbb {Z}_2^n$ such that $w(u) = w(v)$, the equality $P(u)=P(v)$ holds. Thus, from a probabilistic point of view, it does not matter which element of the set $\{u \in A \mid w(u) = k\}$ we choose to work with.

The element $\min (A)$ ($\max (A)$) is the smallest (biggest) integer of the set A, while $\min _w(A)$ ($\max _w(A)$) is an element from A that has the smallest (biggest) hamming weight. We say that a pair of sets $(S_0,S_1)$ is an equal partition of the set S if the following hold: $S = S_1 \cup S_2$, $S_1 \cap S_2 = \emptyset$ and $|S_1| = |S_2|$.

To ease description, we use the notation $C_k^n$ to denote binomial coefficients. Pascal’s identity states that $C_k^n = C_k^{n-1} + C_{k-1}^{n-1}$, where $1 \le k \le n$. Note that $|\{u \in \mathbb {Z}_2^n \mid w(u) = k\}| = C_k^n$.

In this paper, we consider a digital filter to be a mapping from $\mathbb {Z}_2^{n}$ to $\mathbb {Z}_2$. If we continuously apply a filter to data generated by a RNG⁴, then three types of filters arise:

• bias amplifier - the output data has a bigger bias than the input data;

• neutral filter - the output data has the the same bias as the input data;

• bias corrector⁵ - the output data has a smaller bias than the input data.

Let $(S_0,S_1)$ be an equal partition of a set S. Let D be a digital filter such that it maps $S_0$ and $S_1$ to 0 and 1, respectively (see Table 1). Also, let $\varepsilon _D$ be the output bias of D. We say that a bias amplifier is maximal if $\varepsilon _D$ is maximal over all the equal partitions of $\mathbb {Z}_2^n$. To compare bias amplifiers we measure the distance between $P(S_1)$ and $P(S_0)$.

Table 1. Conversion table.

Before stating our results, some restrictions are needed. If the input bits are unbiased (i.e. $P_0 = \frac{1}{2}$) or have a maximum bias (i.e. $P_0 = 0$ or $P_1 = 0$) we require the filter to maintain the original bias. If one replaces a bias corrector with a bias amplifier, the amplifier must behave as the corrector when the RNG has bias 0 or $\frac{1}{2}$. The last requirement is that the filter amplifies the bias in the direction that it already is. Without loss of generality, we assume that the bias is towards 1.

3 Greedy Bias Amplifiers

In this section we generalize and improve the bias amplifier described in [15]. We first present a neutral filter and based on it we develop a maximal bias amplifier. We can easily transform one into the other by changing the conversion table.

Lemma 1

Let $S_0 = \{u \in \mathbb {Z}_2^n \mid u = 0 \Vert v, v \in \mathbb {Z}_2^{n-1}\}$ and $S_1 = \{u \in \mathbb {Z}_2^n \mid u = 1 \Vert v, v \in \mathbb {Z}_2^{n-1}\}$. Then $P(S_0) = P_0$ and $P(S_1) = P_1$.

Proof

Since we are working with i.i.d. random bits the following holds

$$\begin{aligned} P(S_0)&= \sum _{v \in \mathbb {Z}_2^{n-1}} P(0 \Vert v) = \sum _{v \in \mathbb {Z}_2^{n-1}} P_0 P(v) = P_0 \sum _{v \in \mathbb {Z}_2^{n-1}} P(v) = P_0. \end{aligned}$$

Similarly, we obtain $P(S_1) = P_1$.    $\square$

Using Lemma 1 we can devise a neutral filter N by mapping all the elements of $S_0$ and $S_1$ to 0 and 1, respectively. Starting from the equal partition $(S_0,S_1)$ (Lemma 1), using a greedy algorithm (Algorithm 1), we devise a new equal partition that serves as the core of a maximal bias amplifier.

Lemma 2

Let k be a positive integer and let $(S_0,S_1)$ be the output of Algorithm 1. Then the following properties hold

• 1. If $n=2k+1$ then $S_0 = \{u \mid 0 \le w(u) \le k\}$ and $S_1 = \{u \mid k+1 \le w(u) \le n\}$. Also, $P(S_0) = \sum _{i=0}^k C_i^n (P_0)^{n-i} (P_1)^{i}$ and $P(S_1) = \sum _{i=0}^k C_i^n (P_0)^{i} (P_1)^{n-i}$.

• 2. If $n=2k$ then $S_0 = \{u \mid 0 \le w(u) \le k-1\} \cup T_0$ and $S_1 = \{u \mid k+1 \le w(u) \le n\} \cup T_1$, where $(T_0, T_1)$ is an equal partition of $\{u \in \mathbb {Z}_2^n \mid w(u) = k\}$. Also, $P(S_0) = \sum _{i=0}^{k-1} C_i^n (P_0)^{n-i} (P_1)^{i} + \frac{C_k^n}{2} (P_0 P_1)^k$ and $P(S_1) = \sum _{i=0}^{k-1} C_i^n (P_0)^{i} (P_1)^{n-i} + \frac{C_k^n}{2} (P_0 P_1)^k$.

• 3. If $\varepsilon = 0$ then $P(S_0) = P(S_1) = \frac{1}{2}$ and if $\varepsilon = \frac{1}{2}$ then $P(S_0) = 0$ and $P(S_1) = 1$.

Proof

During the while loop Algorithm 1 swaps the elements whose weight is written in Column 2, Table 2 with the elements that have their weight written in Column 3, Table 2.

Table 2. Operations performed during the while loop.

The while loop ends when $w(\alpha ) \ge w(\beta )$. According to Table 2, this is equivalent with $n-i \ge i$. When $n = 2k+1$ we obtain that the while loop stops when $i \le k+1$. When $n = 2k$ the loop stops when $i \le k$. Thus, we obtain the sets $S_0$ and $S_1$. The probabilities $P(S_0)$ and $P(S_1)$ are a direct consequence of the structure of the sets and the fact that $C_k^n = C_{n-i}^n$. The last item is simply a matter of computation.    $\square$

Lemma 3

Let $(S_0,S_1)$ be the output of Algorithm 1. If we map all the elements of $S_0$ and $S_1$ to 0 and 1, respectively, then we obtain a maximal bias amplifier G.

Proof

According to Lemma 2 all the lowest and highest probability elements are in $S_0$ and $S_1$, respectively. Thus, the statement is true.    $\square$

Lemma 4

Let $(S_0^n,S_1^n)$ be the output of Algorithm 1 for $n = 2k+1$. Then the following hold

• 1. $P(S_0^{n}) = P(S_0^{n+1})$ and $P(S_1^{n}) = P(S_1^{n+1})$.

• 2. $P(S_0^n) - P(S_0^{n+2}) = P(S_1^{n+2}) - P(S_1^n) = 2\varepsilon C_k^n (P_0 P_1)^{k+1}$.

• 3. $P(S_0^{n}) > P(S_0^{n+2})$ and $P(S_1^{n}) < P(S_1^{n+2})$.

• 4. $P(S_1^{n}) - P(S_0^{n}) < P(S_1^{n+2}) - P(S_0^{n+2})$.

Proof

We prove the first statement using induction. When $k=1$ we have $S_0^1 = \{0\}$, $S_1^1 = \{1\}$, $S_0^2 = \{00, 01\}$ and $S_1^2 = \{10, 11\}$. Using Lemma 1, we obtain $P(S_0^1) = P_0 = P(S_0^2)$ and $P(S_1^1) = P_1 = P(S_1^2)$. Thus, proving the statement for the case $k=1$.

We now assume that the statement is true for k (i.e. $P(S_0^{n}) = P(S_0^{n+1})$ and $P(S_1^{n}) = P(S_1^{n+1})$) and we it for $k+1$. Applying Pascal’s identity twice to $P(S_0^{n+2})$ we obtain

$$\begin{aligned} P(S_0^{n+2})&= \sum _{i=0}^{k+1} C_i^{n+2} (P_0)^{n+2-i} (P_1)^{i} = (P_0)^{n+2} + (n+2) (P_0)^{n+1} P_1 \nonumber \\&+\sum _{i=2}^{k+1} (C_i^n+2C_{i-1}^n+C_{i-2}^n) (P_0)^{n+2-i} (P_1)^{i}. \end{aligned}$$

(1)

We rewrite Eqs.  (1) as a sum of $S^1, S^2, S^3$ (described next):

$$\begin{aligned} S^1&= (P_0)^{n+2} +n (P_0)^{n+1} P_1 + \sum _{i=2}^{k+1} C_i^n (P_0)^{n+2-i} (P_1)^{i} \\ \nonumber&= (P_0)^2 P(S_0^n) + C_{k+1}^n (P_0)^{n+1-k} (P_1)^{k+1}, \end{aligned}$$

(2)

$$\begin{aligned} S^2&= 2 (P_0)^{n+1} P_1 + 2\sum _{i=2}^{k+1} C_{i-1}^n (P_0)^{n+2-i} (P_1)^{i} \\ \nonumber&= 2\sum _{i=0}^k C_i^n (P_0)^{n+1-i} (P_1)^{i+1} = 2 P_0 P_1 P(S_0^n), \end{aligned}$$

(3)

$$\begin{aligned} S^3&= \sum _{i=2}^{k+1} C_{i-2}^n (P_0)^{n+2-i} (P_1)^{i} = \sum _{i=0}^{k-1} C_i^n (P_0)^{n-i} (P_1)^{i+2} \\ \nonumber&= (P_1)^2 P(S_0^n) - C_k^n (P_0)^{n-k} (P_1)^{k+2}. \end{aligned}$$

(4)

Reassembling Eqs. (2) to (4) we obtain

$$\begin{aligned} P(S_0^{n+2})&= P(S_0^n) + C_{k+1}^n (P_0)^{n+1-k} (P_1)^{k+1} - C_k^n (P_0)^{n-k} (P_1)^{k+2} \\&= P(S_0^n) - 2\varepsilon C_k^n (P_0 P_1)^{k+1}. \nonumber \end{aligned}$$

(5)

Applying Pascal’s identity twice to $P(S_0^{n+3})$ we obtain

$$\begin{aligned} P(S_0^{n+3})&= \sum _{i=0}^{k+1} C_i^{n+3} (P_0)^{n+3-i} (P_1)^{i} + \frac{C_{k+2}^{n+3}}{2} (P_0 P_1)^{k+2} \\&= (P_0)^{n+3} + (n+3) (P_0)^{n+2} P_1 \nonumber \\&+ \sum _{i=2}^{k+1} (C_i^{n+1}+2C_{i-1}^{n+1}+C_{i-2}^{n+1}) (P_0)^{n+3-i} (P_1)^{i} + \frac{C_{k+2}^{n+3}}{2} (P_0 P_1)^{k+2}. \nonumber \end{aligned}$$

(6)

Let $\alpha = \sum _{i=0}^{k} C_i^{n+1} (P_0)^{n+1-i}(P_1)^{i}$. We rewrite Eq.  (6) as a sum of $S^4, S^5, S^6$ (described next):

$$\begin{aligned} S^4&= (P_0)^{n+3} + (n+1) (P_0)^{n+2} P_1 + \sum _{i=2}^{k+1} C_i^{n+1} (P_0)^{n+3-i} (P_1)^{i} \\ \nonumber&= (P_0)^2 \alpha + C_{k+1}^{n+1} (P_0)^{n+2-k} (P_1)^{k+1},\end{aligned}$$

(7)

$$\begin{aligned} S^5&= 2 (P_0)^{n+2} P_1 + 2\sum _{i=2}^{k+1} C_{i-1}^{n+1} (P_0)^{n+3-i} (P_1)^{i} \\ \nonumber&= 2\sum _{i=0}^k C_i^{n+1} (P_0)^{n+2-i} (P_1)^{i+1} = 2 P_0 P_1 \alpha ,\end{aligned}$$

(8)

$$\begin{aligned} S^6&= \sum _{i=2}^{k+1} C_{i-2}^{n+1} (P_0)^{n+3-i} (P_1)^{i} = \sum _{i=0}^{k-1} C_i^{n+1} (P_0)^{n+1-i} (P_1)^{i+2} \\ \nonumber&= (P_1)^2 \alpha - C_k^{n+1} (P_0)^{n+1-k} (P_1)^{k+2}. \end{aligned}$$

(9)

Reassembling Eqs. (7) and (9) we obtain

$$\begin{aligned} P(S_0^{n+3})&= P(S_0^{n+1}) + C_{k+1}^{n+1} (P_0)^{n+2-k} (P_1)^{k+1} - C_k^{n+1} (P_0)^{n+1-k} (P_1)^{k+2} \\&- \frac{C_{k+1}^{n+1}}{2} (P_0 P_1)^{k+1} + \frac{C_{k+2}^{n+3}}{2} (P_0 P_1)^{k+2} \nonumber \\&= P(S_0^{n+1}) - C_k^n (P_0 P_1)^{k+1} \left\{ \frac{n+1}{k+1}\left[ (P_0)^{2}-\frac{1}{2} \right] \right. \nonumber \\&+ \left. P_0 P_1 \left[ -\frac{n+1}{k+2} + \frac{(n+1)(n+2)(n+3)}{2(k+1)(k+2)(k+2)}\right] \right\} \nonumber \\&= P(S_0^{n+1}) - C_k^n (P_0 P_1)^{k+1} \left\{ 2\left[ (P_0)^{2}-\frac{1}{2} \right] +2P_0 P_1 \right\} \nonumber \\&= P(S_0^{n+1}) - 2\varepsilon C_k^n (P_0 P_1)^{k+1}. \nonumber \end{aligned}$$

(10)

Applying the induction step to Eqs.  (5) and (10) we obtain that $P(S_0^{n+2}) = P(S_0^{n+3})$. The following equality is a consequence of the complement rule

$$\begin{aligned} P(S_1^{n+2}) = 1 - P(S_0^{n+2}) = 1 - P(S_0^{n+3}) = P(S_1^{n+3}). \end{aligned}$$

This completes the proof the first statement. The remaining statements are a direct consequence of Eq. (5) and the complement rule.    $\square$

Corollary 1

Let $(S_0^n,S_1^n)$ be the output of Algorithm 1 for $n = 2k+1$. Then $P(S_0^{n}) - P(S_0^{n+2}) > P(S_0^{n+2}) - P(S_0^{n+4})$ and $P(S_1^{n+2}) - P(S_1^{n}) > P(S_1^{n+4}) - P(S_1^{n+2})$.

Proof

Using Lemma 4 we obtain that $P(S_0^{n}) - P(S_0^{n+2}) > P(S_0^{n+2}) - P(S_0^{n+4})$ is equivalent with $2\varepsilon C_k^n (P_0 P_1)^{k+1} > 2\varepsilon C_{k+1}^{n+2} (P_0 P_1)^{k+2}$. Rewriting the inequality we obtain

$$\begin{aligned} 1 > \frac{(2k+2)(2k+3)}{(k+1)(k+2)} P_0 P_1. \end{aligned}$$

The proof is concluded by observing that

$$\begin{aligned} \frac{(2k+2)(2k+3)}{(k+1)(k+2)} P_0 P_1 < 4 \left( \frac{1}{4}-\varepsilon ^2\right) = 1 - 4\varepsilon ^2 \le 1. \end{aligned}$$

   $\square$

Figure 1(a) and (b) are a graphical representation of Lemma 4 ($n \le 17$) and Corollary 1 ($n \le 15$), respectively. The x-axis represents the original bias $\epsilon$, while the y-axis represents $P(S_1^n)$ (Fig. 1(a)) and $P(S_1^{n+2}) - P(S_1^{n})$ (Fig. 1(b)).

Fig. 1.

Greedy amplifier.

Using the properties stated in Lemmas 2 and 4, we will next describe an equivalent and simplified version of Algorithm 1. Note that devising a greedy bias amplifier only makes sense when n is odd.

4 Von Neumann Bias Amplifier

Von Neumann introduced in [14] a simple, yet effective method for correcting the bias of a RNG. Each time the RNG generates two random bits $b_1$ and $b_2$, the filter outputs $b_1$ if and only if $b_1 \ne b_2$. It is easy to see that $P(b_1b_2 = 01) = P(b_1b_2 = 10) = P_0P_1$. Thus, the bias of the output data is 0. We further generalize Von Neumann’s method and explain how to replace it’s conversion table in order to obtain a maximal bias amplifier. Through this section we will restrict n to be of the form 2k, where k is a positive integer.

Lemma 5

Let $V = \{u \in \mathbb {Z}_2^n \mid w(u) = k\}$ and let $(V_0, V_1)$ be an equal partition of V. Then $P(V_0) = P(V_1) = \frac{C_k^n}{2}(P_0 P_1)^k$.

Proof

Since $(V_0, V_1)$ is an equal partition of V, we obtain that $|V_0| = |V_1| = \frac{|V|}{2} = \frac{C_k^n}{2}$. Note that $P(u) = (P_0 P_1)^k$, for any $u \in V$. Combining these two facts we obtain the statement of the lemma.    $\square$

Using Lemma 5 we can devise a corrector filter⁶ $V_c$ by mapping all the elements of $V_0$ and $V_1$ to 0 and 1, respectively. In Algorithm 3 we provide an example of how to generate a pair $(V_0,V_1)$.

We further show that the probabilities $V_0$ and $V_1$ get smaller if we increase n. This translates in a lower bit rate if we apply $V_c$. Note that increasing n does not change the bias of the output data, thus making $V_c$⁷ useless in practice if used only for correcting biases.

Lemma 6

Let $(V_0^n,V_1^n)$ be the output of Algorithm 3 for $n = 2k$. Then $P(V_0^n) > P(V_0^{n+2})$.

Proof

We remark that $P(V_0^n) > P(V_0^{n+2})$ is equivalent with

$$\begin{aligned} 1 > \frac{(2k+1)(2k+2)}{(k+1)(k+1)} P_0 P_1. \end{aligned}$$

The proof is now similar to Corollary 1 and thus is omitted.    $\square$

Figure 2 is a graphical representation of Lemma 6 ($n \le 18$). The x-axis represents the original bias $\epsilon$, while the y-axis represents $P(V_0^n)$.

Fig. 2.

Probability of $V_0^n$ and $V_1^n$.

Note that when $P_0 = 0$ or $P_1 = 0$ we obtain $P(V_0) = P(V_1) = 0$. When constructing a bias amplifier $V_a$ we must have the same behavior. Thus, the strings we use to construct $V_a$ need to contain at least a 0 and an 1. When $n=2$ the only strings that contain 0 and 1 are 01 and 10, but these are the basis for the Von Neumann bias corrector. Hence, when $n=2$ there are no bias amplifiers. This leads to the restriction $n \ge 4$. We again use a greedy approach (Algorithm 4) and devise a core for $V_a$.

Lemma 7

Let x be an integer such that $\sum _{i=1}^{x} C_i^n< C_k^n/2 < \sum _{i=1}^{x+1} C_i^n$. Define $y = C_k^n/2 - \sum _i^x C_i^n$, $W_0 \subset \{u \in \mathbb {Z}_2^n \mid w(u) = x+1\}$, $W_1 \subset \{u \in \mathbb {Z}_2^n \mid w(u) = n-x-1\}$, such that $|W_0| = |W_1| = y$. Also, let $(V_0,V_1)$ be the output of Algorithm 4 . Then the following properties hold

• 1. $V_0 = \{u \mid 1 \le w(u) \le x\} \cup W_0$ and $V_1 = \{u \mid n-x \le w(u) \le n-1 \} \cup W_1$.

• 2. $P(V_0) = \sum _{i=1}^{x} C_i^n (P_0)^{n-i} (P_1)^{i} + y (P_0)^{n-x-1} (P_1)^{x+1}$ and $P(V_1) =$ $\sum _{i=1}^x C_i^n (P_0)^{i} (P_1)^{n-i}+ y(P_0)^{x+1} (P_1)^{n-x-1}$.

• 3. If $\varepsilon = 0$ then $P(S_0) = P(S_1) = \frac{1}{2}$ and if $\varepsilon = \frac{1}{2}$ then $P_0 = 0$ and $P_1 = 1$.

Proof

The proof is a direct consequence of Algorithm 4 and thus is omitted.    $\square$

Lemma 8

Let $(V_0,V_1)$ be the output of Algorithm 4. If we map all the elements of $V_0$ and $V_1$ to 0 and 1, respectively, then we obtain a maximal bias amplifier $V_a$.

Proof

According to Lemma 7 all the lowest and highest probability elements are in $V_0$ and $V_1$, respectively. Thus, the statement is true.    $\square$

Figure 3 is a graphical representation of Lemma 7 ($n \le 18$). The x-axis represents the original bias $\epsilon$, while the y-axis in Fig. 3(a) and (b) represents $P(V_0^n)$ and $P(V_1^n)$, respectively.

Fig. 3.

Von Neumann amplifier.

Unfortunately, due to the nature of x and y, the best we could do is to heuristically provide a graphical representation of Conjecture 1 (Fig. 4). We could not theoretically prove it in general.

Conjecture 1

Let n be even, $(S_0^{n-1},S_1^{n-1})$ be the output of Algorithm 1 for $n-1$ and $(V_0^{n},V_1^{n})$ be the output of Algorithm 4 for n. Denote by $M^n = [P(V_1^n) - P(V_0^n)]\cdot [P(V_1^n) + P(V_0^n)]^{-1}$. Then $M^n < M^{n+2}$ and $P(S_1^{n-1}) - P(S_0^{n-1}) < M^n$.

Note that in the case of greedy amplifiers the metric $[P(S_1^{n-1}) - P(S_0^{n-1})]\cdot [P(S_1^{n-1}) + P(S_0^{n-1})]^{-1}$ is equal to $P(S_1^{n-1}) - P(S_0^{n-1})$. Thus, Conjecture 1 states that the Von Neumann amplifier for a given n is better at amplifying $\varepsilon$ than its greedy counterpart. We chose to state the conjecture such that it is true for all $n\ge 4$, but, from Fig. 4, we can observe that as n grows the Von Neumann amplifier becomes better at amplifying $\epsilon$⁸. Note that in Fig. 4 the x-axis represents the original bias $\epsilon$, while the y-axis represents the values $P(S_1^{n-1}) - P(S_0^{n-1})$ (interrupted line) and $M^n$ (continuous line).

Fig. 4.

Comparing greedy amplifiers (interrupted line) with Von Neumann amplifiers (continuous line).

5 Applications

5.1 The Good

RNG standards [11, 13] require manufactures to implement some early detection mechanism for entropy failure. Health tests represent one such method for detecting major failures. There are two categories of health tests: startup tests and continuous tests. The former are one time tests conducted before the RNG starts producing outputs, while the latter are tests performed in the background during normal operation.

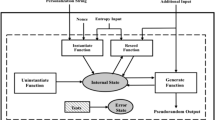
We propose a generic architecture for implementing health tests (Fig. 5). We first store data D (obtained from the noise source) in a buffer, then we apply a bias amplifier to it and obtain data $D_a$. Next, we apply some lightweight tests on $D_a$. If the tests are passed, the RNG outputs D, otherwise D is discarded. Note that the bias amplifier can be implemented as a lookup table, thus obtaining no processing overhead at the expense of $\mathcal O(2^n)$ memory.

Fig. 5.

Generic architecture for implementing health tests.

In our instantiations we used the health tests implemented in Intel’s processors [10]. Intel’s health tests $H_i$ use a sliding window and count how many times each of the six different bit patterns (Column 1, Table 3) appear in a 256 bit sample. An example of allowable margins for the six patterns can be found in Column 2, Table 3. The thresholds mentioned in Tables 3 and 4 were computed using $10^6$ 256 bit samples generated using the default RNG from the GMP library [3].

We first propose a continuous test using the greedy amplifiers described in Sect. 3. Depending on the available memory we can use one of the greedy amplifiers and then apply $H_i$. Note that n should be odd due to Lemma 4. If the health test are implemented in a processor it is much easier to use $n = 4, 8, 16$. From the health bounds presented in Table 3, we can observe that the differences between data without amplification and data with amplification are not significant. Thus, one can easily update an existing good RNG⁹ by adding an extra buffer and an amplification module, while leaving the health bounds intact. Note that due to the unpredictable number of output bits produced by a Von Neumann amplifier, greedy amplifiers are better suited for continuous testing.

Table 3. Health bounds for greedy amplifiers (amp.).

If the design of the RNG has a Von Neumann module, then Von Neumann amplifiers can be used to devise a startup test. Before entering normal operation, the Von Neumann module can be instantiated using the conversion table of the corresponding amplifier. For example, when $n=4$ one would use $V_0 = \{0001, 0010, 0100\}$ and $V_1 = \{0111, 1011, 1101\}$¹⁰ instead of $V_0 = \{0011, 0101, 0110\}$ and $V_1 = \{1001, 1010, 1100\}$¹¹. The resulting data can then be tested using $H_i$ and if the test pass the RNG will discard the data and enter normal operation. Note that the first buffer from Fig. 5 is not necessary in this case. Note that Von Neumann amplifiers require $n>2$, thus the speed of the RNG will drop. This can be acceptable if the data speed needed for raw data permits it, the RNG generates data much faster than the connecting cables are able to transmit or the raw data is further used by a pseudo-random number generator (PRNG).

Table 4. Health bounds for Von Neumann correctors (corr.) and amplifiers (amp.).

5.2 The Bad

One can easily turn the benign architecture presented in Fig. 5 into a malicious architecture (Fig. 6). In the new proposed configuration, health tests always output pass and instead of outputting D the system outputs $D_a$.

The malicious configuration can be justified as a bug and can be obtained from the original architecture either by commenting some code lines (similarly to [6]) or by manipulating data buffers (similarly to [7]). Note that code inspection or reverse engineering will reveal these so called bugs. A partial solution to detection can be implementing the architecture in a tamper proof device and deleting the code if someone tinkers with the device. Another partial solution is embedding the architecture as a submodule in a more complex architecture (similarly to [6]). This solution is plausible due to the sheer complexity of open-source software and the small number of experts who review them [5].

Fig. 6.

Generic architecture for infecting RNGs.

Another problem is that the RNG will output $D_a$s instead of Ds and this translates to lower data rates. A possible solution to this problem is to use $D_a$ as a seed for a PRNG and then output the data produced by the PRNG. Thus, raw data is never exposed. A problem with this approach is that in most cases the PRNG will also mask the bias. The only case that is compatible with this approach is when the bias is large. Therefore one can simply use an intelligent brute force to find the seed. Hence, breaking the system.

A more suitable approach to the aforementioned problem is to use a pace regulator [9]. This method uses an intermediary buffer to store data and supplies the data consumer with a constant stream of bits. Unfortunately, if data requirements are high, then the regulator will require a lot of memory and in some cases the intermediary buffer will be depleted. Thus, failing to provide data.

A solution specific to greedy amplifiers is to implement in all devices a neutral filter after D and output the resulting data $D_n$. Thus, when a malicious version of the RNG is required, one can simply replace the conversion table of the neutral filter with the conversion table of the corresponding bias amplifier. For example, when $n=3$ one would change $S_0 = \{000, 001, 010, 100\}$ and $S_1 = \{111, 110, 101, 100\}$¹² with $S_0 = \{000, 001, 010, 100\}$ and $S_1 = \{111, 110, 101, 011\}$¹³. It is easy to see that in this case both $D_n$ and $D_a$ have the same frequency.

Since we are modifying the statistical properties of the raw data, a simple method for detecting changes is black box statistical testing (for example using [2]). Thus, if a user is getting suspicious he can detect the “bugs”. Again, a partial solution is to implement the malicious architecture as a submodule inside a more complex architecture either in tamper proof devices, either in complex software. Thus, eliminating the user’s access to raw data.

6 Conclusions and Future Work

In our paper we studied and extended bias amplifiers, compared their performance and provided some possible applications for them. Even thou in its infancy, this area of research provides insight into what can go wrong with a RNG.

A possible future direction would be to extended our results to other randomness extractors. Of particular interest, is finding a method to turn a block cipher or a hash function¹⁴ into an amplifier.

A Experimental Results

To test the configuration proposed in Sect. 5.1, Fig. 5 and obtain some metrics (Table 5) we conducted a series of experiments. More precisely, we generated 105000 256 bit samples using the Bernoulli distribution instantiated with the Mersenne Twister engine (mt19937) found in the C++ random library [1]. Then, we applied the bias amplifying filters from Table 3 and counted how many samples are marked pass. In the case of raw data, a sample is marked pass¹⁵ if it passes the $H_i$ test from Column 1, Table 3. In the case of bias amplification, if a 256 bit buffer $b_a$ from $D_a$ passes $H_i$, all the input buffers that where used to produce $b_a$ are marked pass. Note that to implement our filters we used lookup tables and thus we had no performance overhead.

From Table 5 we can easily see that when the bias is increased, the number of samples that are marked pass is lower than $H_i$ in the case of greedy amplifiers. Also, note that the rejection rate is higher as n increases. Thus, enabling us to have an early detection mechanism for RNG failure.

Table 5. Greedy amplifiers (amp.) metrics.

We also conducted a series of experiments to test the performance of the startup test proposed in Sect. 5.1. This time, we generated data until we obtained 1000 256-bit samples, applied the bias correcting/amplifying filters from Table 4 and counted how many of these samples pass the $H_i$ test from Column 1, Table 3. Another metric that we computed is the number of input bits required to generate one output bit.

Note that in Table 6 we only wrote the $n=2$ corrector, since for $n=4, 6$ the results are almost identical. From Table 6 we can easily observe that when the bias is increased the number of samples that pass $H_i$ is lower than the corrector in the case of Von Neumann amplifiers. As in the case of greedy amplifiers, we can observe that the rejection rate is higher as n increases. The experimental data also shows that Von Neumann amplifiers perform better than the greedy amplifiers when rejecting bad samples.

Table 6. Von Neumann correctors (corr.) and amplifiers (amp.) metrics.

Table 7. Von Neumann correctors (corr.) and amplifiers (amp.) throughput.

In Table 7 we can see that more data is required to generate one bit as n grows. When the bias increases, we can observe that compared to Von Neumann correctors the throughput of the corresponding amplifiers is better. Thus, besides having an early detection mechanism, it also takes less time to detect if an RNG is broken if we use a Von Neumann amplifier.