Abstract
Since (t, n)-threshold secret sharing (SS) was initially proposed by Shamir and Blakley separately in 1979, it has been widely used in many aspects. Later on, Asmuth and Bloom presented a (t, n)-threshold SS scheme based on the Chinese Remainder Theorem (CRT) for integers in 1983. However, compared with the most popular Shamir’s thresholdtn SS scheme, existing CRT based schemes have a lower information rate, moreover, they are harder to construct due to the stringent condition on moduli. To overcome these shortcomings of CRT based schemes, (1) we first propose a generalized (t, n)-threshold SS scheme based on the CRT for polynomial ring over a finite field. We show that our scheme is ideal, i.e., it is perfect in security and has the information rate 1. Comparison show that our scheme has a better information rate and is easier to construct compared with the existing threshold SS schemes based on the CRT for integers. (2) We prove that Shamir’s scheme, which is based on the Lagrange interpolation, is a special case of our scheme. Therefore, we establish the connection among threshold schemes based on the Lagrange interpolation, schemes based on the CRT for integers and our scheme. (3) As a natural extension of our threshold scheme, we present a weighted threshold SS scheme based on the CRT for polynomial rings, which inherits the above advantages of our threshold scheme over existing weighted schemes based on the CRT for integers.
Supported partially by National NSF of China 61572454,61572453,61520106007 and National Key R&D Program of China 2018YFB0803400.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Secret sharing (SS) was first introduced respectively by Shamir [29] and Blakley [4] in 1979 to construct robust key management schemes for cryptographic systems. Shamir’s scheme is constructed based on the Lagrange interpolation polynomial, as a \((t,n)\)-threshold SS scheme (i.e., (t, n)-SS), it divides a secret into n shares and distributes each share to one of n parties called shareholders; only t or more shareholders pooling their shares together can recover the secret while \(t-1\) or less shareholders cannot obtain any information about the secret. So far, many schemes [10, 18, 19, 27, 34] have been proposed based on Shamir’s scheme. Later on, threshold schemes based on the Chinese Remainder Theorem (CRT) for integer ring were proposed by Mignotte [25] and Asmuth-Bloom [1].
Different from Shamir’s scheme, Mignotte’s scheme and Asmuth-Bloom’s scheme illustrated a new method to construct (t, n)-threshold SS schemes using the CRT for integers. Both schemes are highly similar except that the latter improves the former in perfectness of security. Therefore, Asmuth-Bloom’ scheme is our main concern among CRT based SS schemes in this paper. In nature, CRT-based schemes are capable of assigning shares of distinct size to different shareholders, this capability can in turn be used to implement new functionality, e.g., the weighted schemes of [15, 21, 35]. In constructing weighted SS schemes, CRT-based SS schemes allow a shareholder to possess only one share each. In contrast, Shamir’s scheme needs to allocate trivially multiple shares to a shareholder, who has the weight more than 1. Moreover, the shareholder leaking any of its shares may cause the disclosure of the secret.
Asmuth-Bloom’s scheme has become a popular and fundamental schemes. Based on the scheme, a lot of work [16,17,18, 22, 24] has been done to extend the original idea and meet different requirements of practical applications. One type of extension is to construct new access structures, e.g., the general access structure [18] and the multipartite scheme [16]. Another type of extension aims to improve functionality, e.g., the verifiable SS [17, 24] to prevent malicious action of dishonest shareholders and the proactive secret sharing for strengthening the security.
As we all know, Shamir’s scheme is based on Lagrange interpolation and thus is easy to construct. Moreover, it is an ideal SS scheme, i.e., it is perfect in security and has the maximum information rate 1. Roughly speaking, information rate is the ratio of secret to share in size, which denotes the information efficiency of secret sharing. In comparison, the CRT-based Asmuth-Bloom’s scheme, on one hand, is lower in information rate since each share is larger than the secret in size; on the other hand, it is difficult to construct because the scheme requires a series of pairwise coprime integers satisfying some stringent condition.
In a word, Shamir’s scheme is ideal and easy to construct while Asmuth-Bloom’s scheme is not ideal, hard to construct but more natural and neat in constructing weighted SS scheme. In this case, we are faced the following 2 questions,
-
Is there any CRT-based SS scheme which is ideal as Shamir’s scheme?
-
If such a scheme exists, how to construct it in practice? and what is the connection in theory among Shamir’ scheme, Asmuth-Bloom’s scheme and the new scheme?
To answer the above questions, we need to study new CRT based schemes free from the above mentioned drawbacks in Asmuth-Bloom’s scheme. To this end, this paper mainly focuses on constructing a generalized (t, n)-threshold SS scheme based on the CRT for the polynomial ring and further finds out the connection among these (t, n)-threshold SS schemes. Our contribution can be summarized as follows
-
We propose a generalized (t, n)-threshold SS scheme based on the CRT for the polynomial ring over a finite field. Our scheme is perfect in security and has the information rate 1. Compared with Asmuth-Bloom’s scheme, it is better in information rate, easier to construct and more computationally efficient. Therefore, our scheme can serve as a better substitution for Asmuth-Bloom’s scheme. That is, existing schemes based on Asmuth-Bloom’s scheme are allowed to base themselves on our scheme to overcome the above drawbacks inherited from Asmuth-Bloom’s scheme.
-
We show that Shamir’s scheme is a special case of our scheme. As a result, we establish the connection among (t, n) threshold SS schemes based on Lagrange interpolation polynomial (the family of Shamir’s scheme), CRT for integers (the family of Asmuth-Bloom’s scheme) and CRT for polynomial rings (our proposed scheme).
-
We present a weighted SS scheme based on the above proposed threshold scheme. Compared with [15, 21, 35], which are based on Asmuth-Bloom’s scheme, our new weighted scheme enjoys advantages inherited from our (t, n) threshold SS scheme, which illustrates the power of our threshold scheme as a better base than Asmuth-Bloom’s scheme.
The rest of this paper is organized as follows: Sect. 2 introduces some preliminaries about secret sharing and the CRT. In Sect. 3, we present our threshold scheme and compare it with Shamir’s scheme and Asmuth-Bloom’s scheme. Section 4 shows that Shamir’s scheme is a special case of our threshold scheme. In Sect. 5, a weighted threshold scheme is given and compared with other existing CRT based schemes. Finally, Sect. 6 concludes our work.
2 Preliminaries
In this section, we introduce some fundamentals as a preliminary. Subsection 2.1 introduces some notations for convenience. In Subsect. 2.2, the CRT for different rings are discussed. Subsection 2.3 is devoted to some results on the irreducible polynomials in the polynomial ring over a finite field. We introduce some fundamental notions about secret sharing in Subsect. 2.4. Finally, Asmuth-Bloom’s scheme and Shamir’s scheme are reviewed in Subsects. 2.5 and 2.6 respectively.
2.1 Notation
Here, we introduce some notations that will be used all the way.
-
Let \(\mathbb {Z}\) denote the usual ring of integers. Let \(n \in \mathbb {Z}\), [n] denotes the set \(\{ 1,2,\dots , n \}\) of n elements.
-
Let \(p \in \mathbb {Z}\) be a prime number, \( {\mathbb {F}_{p}} \) denotes the finite field of p elements.
-
Let R be some ring, for any \(a, b \in R\),
 denotes the principal ideal generated by a. Also, \(a \mid b\) means that a divides b, that is, there is \(c \in R\) such that \(b=ac\).
denotes the principal ideal generated by a. Also, \(a \mid b\) means that a divides b, that is, there is \(c \in R\) such that \(b=ac\). -
Let R be some ring, R[x] denotes the univariate polynomial ring in the variable x over R. For any \(f(x) \in R[x]\), \(\deg (f(x))\) represents the degree of f(x).
-
Let I be an ideal of a ring R and \(x, y \in R\), \(x \equiv y \pmod {I}\) means that \(x-y \in I\). If
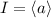 is a principal ideal for some \(a \in R\), it is also written as \(x \equiv y \pmod {a}\).
is a principal ideal for some \(a \in R\), it is also written as \(x \equiv y \pmod {a}\). -
\(\gcd \) denotes the greatest common divisor.
-
Let S be a finite set, \(|{S}|\) denotes the number of elements in S; \(2^S\) denotes the power set of S, that is, \(2^S\) contains all subsets of S as elements.
2.2 The Chinese Remainder Theorem (CRT)
In this subsection, we introduce the CRT for different rings, especially, for \(\mathbb {Z}\) and K[x] with K being a field. This subsection serves as the fundamental of Asmuth-Bloom’s scheme and our proposed scheme.
The Asmuth-Bloom’s scheme is based on the CRT for \(\mathbb {Z}\). Actually, the CRT for \(\mathbb {Z}\) can be generalized to any other ring as follows.
Theorem 1
(Theorem 2.1 of [23]). Let \(I_1, \dots , I_n\) be ideals of a ring R such that \(I_i+I_j = R\) for all \(i, j \in [n], i \ne j\). Given elements \(x_1, \dots , x_n \in R\), there exists \(x \in R\) such that
And x is unique in the sense that if y is another element satisfies all the congruences, then
To have an intuitional understanding of this theorem, we can consider the case when \(R = \mathbb {Z}\). Since \(\mathbb {Z}\) is a principal ideal domain (PID), for all \(i \in [n]\),  for some \(m_i \in \mathbb {Z}\). The condition \(I_i +I_j = R\) becomes that the linear combination of \(m_i\) and \(m_j\) with integer coefficients can represent any integer in \(\mathbb {Z}\), specifically, can represent \(1 \in \mathbb {Z}\), that is \(\gcd (m_i, m_j)=1\). Also, the congruence \(x \equiv x_i \pmod {I_i}\) becomes \(x \equiv x_i \pmod {m_i}\). In conclusion, by letting \(R=\mathbb {Z}\), we have the following ordinary version of the CRT for \(\mathbb {Z}\).
for some \(m_i \in \mathbb {Z}\). The condition \(I_i +I_j = R\) becomes that the linear combination of \(m_i\) and \(m_j\) with integer coefficients can represent any integer in \(\mathbb {Z}\), specifically, can represent \(1 \in \mathbb {Z}\), that is \(\gcd (m_i, m_j)=1\). Also, the congruence \(x \equiv x_i \pmod {I_i}\) becomes \(x \equiv x_i \pmod {m_i}\). In conclusion, by letting \(R=\mathbb {Z}\), we have the following ordinary version of the CRT for \(\mathbb {Z}\).
Theorem 2
Let \(m_1,\dots ,m_n \in \mathbb {Z}\) be pairwise coprime integers. Given integers \(x_1, \dots , x_n \in \mathbb {Z}\), there exists \(x \in \mathbb {Z}\) such that
And x is unique in the sense that if y is another integer satisfies all the congruences, then
Note that the uniqueness also means that x is unique if we only consider numbers in the range \([0,{\prod \nolimits _{i=1}^{n} {m_i}}-1]\).
The reason that we can replace the ideals with the elements generating that ideal is that \(\mathbb {Z}\) is a PID. It is well known that K[x] is also a PID if K is a field. Similarly, we have the following CRT for the ring of polynomials over a field.
Theorem 3
Let K be a field and \(m_1(x), \dots , m_n(x) \in K[x]\) be pairwise coprime polynomials. Given polynomials \(f_1(x), \dots , f_n(x) \in K[x]\), there exists f(x) such that
And f(x) is unique in the sense that if g(x) is another polynomial satisfies all the congruences, then
Note that the uniqueness also means that f(x) is unique if we only consider polynomials of degree less than \(\deg ({\prod \nolimits _{i=1}^{n} {m_i(x)}})\).
The above different versions of CRT (Theorems 1, 2, 3) does not give a concrete method of finding out the exact solution of a given system of congruences. For the most general case, it may be difficult to find such a method. But for Euclidean domains, we can explicitly write out and efficiently compute the solution as the following theorem states.
Theorem 4
(Generalized Algorithm 1.3.11 in [8]). Let R be a Euclidean domain and \(m_1, \dots , m_n \in R\) be pairwise coprime elements. Given elements \(x_1, \dots , x_n \in R\) and a system of congruences
let \(M={\prod \nolimits _{i=1}^{n} {m_i}}\), \(M_i = M/m_i\) and \(a_i \in R\) with \(a_iM_i \equiv 1 \pmod {m_i}\), then,
is a solution of the system of congruences.
2.3 Irreducible Polynomials over a Finite Field
In this subsection, we introduce some existing results about the number of irreducible polynomials and how to find irreducible polynomials in \( {\mathbb {F}_{p}} [x]\). These results enable the practicality of our scheme.
Most results here are derived from the following theorem.
Theorem 5
(Theorem 1 in Chapter 26 of [7]).\(x^{p^n}-x\) is the product of all monic irreducible polynomials in \( {\mathbb {F}_{p}} [x]\) of degree d, for all \(d \mid n\).
First, Theorem 5 shows a way to count the number of irreducible polynomials in \( {\mathbb {F}_{p}} [x]\). Let N(n, p) be the number of monic irreducible polynomials in \( {\mathbb {F}_{p}} [x]\), by Theorem 5, considering the factorization of \(x^{p^n}-x\) and counting the degree, it is clear that
Applying the Mobius inversion formula to Expression 1 results in Theorem 6.
Theorem 6
(Theorem 7 in Chapter 26 of [7]).\(N(n,p)= \frac{1}{n}{\sum \nolimits _{d \mid n}^{} {\mu (n/d)p^d}}\) where \(\mu \) is the Mobius function.
Fixing p, N(n, p) grows rapidly with respect to n, which can be seen in Table 1 and we have Theorem 7 to bound N(n, p).
Theorem 7
(Theorem 19.12 of [31]). For any prime number p, for all \(n \ge 1\), we have
On the other hand, Theorem 5 also results in a primality testing algorithm in \( {\mathbb {F}_{p}} [x]\). Suppose \(f \in {\mathbb {F}_{p}} [x]\) is of degree d, if f is not irreducible, f has an irreducible divisor of degree at most \(k=\lfloor {\frac{d}{2}} \rfloor \). Therefore, by Theorem 5, at least one term in Expression 2
will return a non-trivial divisor of f. Thus, by checking each term in Expression 2, we can determine the primality of f as is in Algorithm 1.

With Algorithm 1, we have the probabilistic Algorithm 2 for finding irreducible polynomials of a given degree d in \( {\mathbb {F}_{p}} [x]\).

Theorem 8
(Theorem 20.2 of [31]). Algorithm 2 takes an expected number of \({\mathcal {O}({d^3 \log d \log p})}\) operations in \( {\mathbb {F}_{p}} \).
2.4 Secret Sharing
Secret sharing was first introduced by Shamir [29] and Blakley [4] in 1979 to construct robust key management schemes for cryptographic systems. Nowadays, it has become a cryptographic primitive and is widely used in many applications, including multiparty computations [3, 9], threshold cryptography [13, 22] and generalized oblivious transfer [30, 33] and so on.
In a secret sharing scheme, a dealer with a secret to share, a set \([n]=\{ 1,2, \dots , n \}\) of n parties and a collection \(\varGamma \subseteq 2^{[n]}\) of authorized subsets are involved. In such a scheme, the dealer generates n shares and allocates each party a share such that
-
any authorized subset of parties in \(\varGamma \) pooling their shares together can determine the secret
-
any subset of parties not in \(\varGamma \) cannot get any information about the secret.
The collection \(\varGamma \) is called the access structure realized by the secret sharing scheme. It is reasonable to assume that if some subset of parties can recover the secret, with any other parties taking participant, they can still recover the secret. That is, if \(A \subseteq [n]\) can recover the secret, then, for any \(B \subseteq [n]\) with \(A \subseteq B\), B is also able to recover the secret. Therefore, \(\varGamma \) has the following monotone property.
And we use Expression 3 as the definition of access structure.
Definition 1
(Access Structure [2]). Let [n] denote a set of parties. A collection \(\varGamma \subseteq 2^{[n]}\) is monotone if \(\forall A \in \varGamma , \forall B \subseteq [n], A \subseteq B \implies B \in \varGamma \). An access structure is a monotone collection of subsets of [n].
Next, we introduce a mathematical model for secret sharing schemes and formalize the meaning of “determining the secret” and “cannot get any information about the secret”.
Definition 2
(Perfect Secret Sharing Scheme [20]). Suppose we have n parties \(\{ 1,2,\dots , n \}\). For a monotone access structure \(\varGamma \subseteq 2^{[n]}\), a perfect secret sharing scheme realizing \(\varGamma \) is a list of discrete random variables \((S, S_1, S_2, \dots , S_n)\) over some finite sample space such that
-
(correctness) - for any \(A \in \varGamma \), \(H(S \mid \{ {S_i} \mid {i \in A} \} ) = 0\)
-
(perfectness) - for any \(B \subseteq [n]\) with \(B \notin \varGamma \), \(H(S \mid \{ {S_i} \mid {i \in B} \} ) = H(S)\)
where \(H(\cdot )\) stands for the Shannon entropy and \(H(\cdot \mid \cdot )\) denotes the conditional entropy.
Naturally, we have the information rate represented by the ratio of the length of the secret to that of shares, which is used to measure the efficiency of each party sharing the secret.
Definition 3
(Information Rate [20]). The (worst-case) information rate of a secret sharing scheme \((S, S_1, \dots , S_n)\) is
A lot of research has been carried out to study the bounds of the information rate for different kinds of access structures. In [6], it was shown that, in any perfect secret sharing scheme, \(H(S) \le H(S_i), i \in [n]\). Therefore, an upper bound for the information rate is \(\rho \le 1\). For a perfect scheme with information rate 1, its share size is at most as small as the secret and we call it an ideal scheme.
Threshold Access Structure: A fundamental case of secret sharing is the threshold case. The access structure realized by a (t, n)-threshold scheme is
That is, only t or more parties can recover the secret while any \(t-1\) or less parties cannot gain any information about the secret.
Weighted Access Structure: The weighted threshold secret sharing is a direct generalization of the threshold case. In a weighted threshold case, a threshold t is set and each party is associated with a positive weight. Only subset of parties, whose sum of weights is larger than or equal to t, can recover the secret while parties, whose sum of weights is less than t, cannot gain any information about the secret. Formally, the access structure realized by a \((t, n,\omega )\)-weighted threshold scheme is
where \({\omega } : {[n]} \rightarrow {\mathbb {N}^+}\) is the weight function and \(\omega (i)\) is the weight of the i-th party. In [26], it was shown that weighted threshold access structures with a positive rational or real weight can always be converted to the same access structure with a weight of positive natural numbers. Therefore, we often only consider the weight as a positive natural number. Usually, we also require the condition that
Otherwise, there is a party knowing the secret and there will be no sharing in some sense. Note that the weighted threshold case degenerates to the basic threshold case if
2.5 Review of Asmuth-Bloom’s Scheme [1]
In this subsection, we review Asmuth-Bloom’s \((t,n)\)-threshold SS scheme.
Share Distribution: The dealer selects integers \(m_0\) and \(m_1< m_2< \dots < m_n\) satisfying Expressions 4 and 5.
The dealer then chooses the secret \(s \in [0, m_0-1]\) and randomly selects an integer \(\alpha \) such that
The share \(s_i\) for the i-th party would be
and is sent to the i-th party privately.
Secret Reconstruction: Suppose t parties \(\{ i_1, \dots , i_t \} \subseteq [n]\) want to recover the secret. They pool their shares together and get the following system of congruences
By Theorems 4 and 2, they would get a unique solution \(x_0\) in the range \([0,{\prod \nolimits _{k=1}^{t} {m_{i_k}}}-1]\). Since \(s+\alpha m_0\) also satisfies this system of congruences and
that is, \(s+\alpha m_0\) is also in the range \([0,{\prod \nolimits _{k=1}^{t} {m_{i_k}}}-1]\). By the uniqueness, \(s+\alpha m_0 = x_0\) and the secret can be recovered by computing \(s = x_0 \bmod m_0\).
There are papers studying the perfectness or the information rate of Asmuth-Bloom’s scheme. In [1], it is shown that the entropy of the secret in Asmuth-Bloom’s scheme decreases “not too much” when \(t-1\) shares are known. In [14], it is advised to choose \(m_0, m_1,\dots , m_n\) being primes as close as possible and it is proved that \(t-2\) shares or less give no information on the secret for a (t, n)-threshold scheme. In [28], it is shown that Asmuth-Bloom’s scheme with moduli being consecutive primes is asymptotically ideal. However, for fixed values of moduli, the scheme always has an lower information rate (less than 1), especially for not too large moduli.
2.6 Review of Shamir’s Scheme [29]
In this subsection, we review Shamir’s \((t,n)\)-threshold SS scheme.
Share Distribution: The dealer selects a prime number p and randomly selects \(t-1\) elements \(a_1,\dots , a_{t-1}\) independently with a uniform distribution over \( {\mathbb {F}_{p}} \). The secret is also some element s from \( {\mathbb {F}_{p}} \). Then the dealer constructs a polynomial
and computes \(s_i=f(i), i \in [n]\) as the private share of the i-th party. Finally, the dealer sends \(s_i\) to the i-th party in private.
Secret Reconstruction: Suppose t parties \(\{ i_1,\dots , i_t \}\) want to recover the secret. They pool their shares together and get the following system of linear equations
Since the coefficient matrix is a Vandermonde square matrix over the field \( {\mathbb {F}_{p}} \) of size \(t \times t\), it is invertible and this system of linear equations has a unique solution. Therefore, they can recover the secret s by solving this system of linear equations.
We have described this scheme from the point of view of solving systems of linear equations. Another way to recover the secret is based on the Lagrange interpolation (Theorem 7.15 of [31]). In this way, f(x) can be written directly as
and the secret is
There are some works studying the perfectness or the information rate of Shamir’s scheme [5, 10, 32]. We show in Sect. 4 that Shamir’s scheme is a special case of our scheme and provide in Subsect. 3.2 a strict proof of the perfectness of our scheme, which also indicates that Shamir’s scheme is perfect. Since the secret and the shares of Shamir’s scheme are all selected in \( {\mathbb {F}_{p}} \), its information rate is obviously 1. Thus, Shamir’s scheme is ideal.
3 Threshold Scheme Based on CRT for Polynomial Ring over Finite Field
In this section, we first propose a \((t,n)\)-threshold SS scheme based on the CRT for polynomial ring over finite field, and show that it can be ideal. Then, we show that Shamir’s scheme is a special case of our scheme, revealing the connection among Shamir’s scheme, Asmuth-Bloom’s scheme and our scheme. Finally, we compare our scheme with the other two schemes.
3.1 The Scheme
In this subsection, we propose a \((t,n)\)-threshold SS scheme. The scheme can be seen as the counterpart of Asmuth-Bloom’s scheme for the polynomial ring over a finite field. It can also be regarded as a generalization of Shamir’s scheme.
Share Distribution: The dealer chooses an integer \(d_0 \ge 1\) and sets \(m_0(x)=x^{d_0}\). The dealer chooses a prime integer p and pairwise coprime polynomials \(m_i(x) \in {\mathbb {F}_{p}} [x], i \in [n]\). Let \(d_i = \deg (m_i(x))\) for all \(i \in [n]\). The polynomials must satisfy each of Expressions 6, 7 and 8.
The secret space is the set
i.e., all polynomials of degree at most \(d_0-1\). Suppose that the dealer has picked his secret \(s(x) \in \mathcal {S}\). Then, the dealer randomly chooses a polynomial \(\alpha (x)\) from the set
and computes
Let \(d_\alpha =\deg (\alpha )\) and \(d_f=\deg (f)\). It is clear that \(d_f \le {\sum \nolimits _{i=1}^{t} {d_i}}-1\). Finally, for each \(i \in [n]\), the dealer computes \(s_i(x) = f(x) \bmod m_i(x)\) as the share for the i-th party and sends \(s_i(x)\) privately to the i-th party.
Share Reconstruction: If t parties \(\{ i_1, \dots , i_t \} \subseteq [n]\) want to reconstruct the secret, they pool their private shares together and get the following system of congruences
According to Theorems 4 and 3, they can solve Expression 9 and get a unique solution \(X_0(x)\) among polynomials of degree less than \(d={\sum \nolimits _{j=1}^{t} {d_{i_j}}}\). Let \(\varPi = {\prod \nolimits _{j=1}^{t} {m_{i_j}(x)}}\). It is clear that
Since f(x) also is a solution of the above system of congruences, by the uniqueness, \(f(x)=X_0(x)\) and they can recover the secret by computing
Before finishing this subsection, we would like to discuss some practical issues. In our scheme, the dealer is required to find a series of n pairwise coprime polynomials in \( {\mathbb {F}_{p}} [x]\). In practice, it is convenient for the dealer to directly select distinct irreducible polynomials of specified degrees and these distinct irreducible polynomials with \(m_0(x)\) are automatically pairwise coprime. By Theorem 7, we know that there are enough irreducible polynomials for this purpose in practice. Also, Algorithm 2 shows an efficient way to accomplish this job.
3.2 Security Analysis
In this subsection, we show that our scheme is perfect. The road map of the proof is as follows.
-
First, Theorem 9 shows that coefficients of the computed f(x) in the scheme regarded as random variables are independently identically distributed(i.i.d) of a uniform distribution over \( {\mathbb {F}_{p}} \), if coefficients of both s(x) and \(\alpha (x)\) are i.i.d with respect to a uniform distribution over \( {\mathbb {F}_{p}} \).
-
Since \(t-1\) parties together can eliminate some choices for f(x), we must show that the number of choices for f(x) left after the elimination is still greater than or equal to the number of choices for s(x). Otherwise, the conditional probability distribution of s(x) under the condition of knowing \(t-1\) shares would not be a uniform distribution. And this part is completed in the proof of Theorem 10.
-
However, what we get so far cannot imply that the conditional probability distribution of s(x) is a uniform one, since Theorem 10 is only a necessary condition. Therefore, we need to study the correspondence between s(x) and f(x) under the relationship that \(f(x) = s(x)+\alpha (x)x^{d_0}\). In particular, we show that after eliminating impossible choices for f(x) with \(t-1\) shares, the number of possible choices for f(x) corresponding to a selected s(x) is a constant. And this part is completed in the proof of Theorem 11.
-
Finally, according to all the results above, we conclude that our scheme is perfect.
Theorem 9
If the coefficients of s(x) and \(\alpha (x)\), regarded as random variables, are independently identically distributed(i.i.d) of a uniform distribution, then, the coefficients of f(x), viewed as random variables, are also i.i.d with respect to a uniform distribution over \( {\mathbb {F}_{p}} \).
Proof
In the scheme, f(x) is computed as
where the coefficients of s(x) and \(\alpha (x)\) are i.i.d with respect to a uniform distribution over \( {\mathbb {F}_{p}} \). Since
-
\(f[i]=s[i]\) for \(0 \le i \le d_0-1\)
-
\(f[i]=\alpha [i-d_0]\) for \(d_0 \le i\)
therefore, coefficients of f are i.i.d of a uniform distribution over \( {\mathbb {F}_{p}} \). \( \Box \)
To show that our scheme is perfect, it suffices to consider the worst case where the \(t-1\) parties \(\{ n, n-1,\dots , n-t+2 \}\) with moduli of the highest degree pool their shares together and try to recover the secret. But they only get the following system of \(t-1\) congruences
By solving Expression 10, they can only find a unique solution \(X_0(x) \in {\mathbb {F}_{p}} [x]\) among polynomials of degree less than \({\sum \nolimits _{i=n-t+2}^{n} {d_{i}}}\). Since f(x) also satisfies Expression 10 and all the moduli are pairwise coprime, let \(\varPi = {\prod \nolimits _{i=n-2+t}^{n} {m_i(x)}}\), they know \(f(x) \equiv X_0(x) \pmod {\varPi }\), that is,
By Expression 11, \(t-1\) parties can eliminate some choices of f(x). We must consider how many possible f(x) still satisfy this equation for given \(X_0(x)\). That is, fixing \(X_0(x)\), we need to find the cardinality of the set
Let \(d = {\sum \nolimits _{i=n-t+2}^{n} {d_i}}\). Let \(\delta ={\sum \nolimits _{i=1}^{t} {d_i}}-d\). It is clear that \(\delta \ge d_0\) by the selection of the parameters \(d_i\) during the scheme construction. We claim that \(|{F}|=p^{\delta }\) as Theorem 10 states. Note that \(|{\mathcal {S}}| = p^{d_0}\) and \(|{F}| \ge |{\mathcal {S}}|\) for the secret space \(\mathcal {S}\).
Theorem 10
\(|{F}|\) is equal to \(p^{\delta }\).
Proof
Any element \(g(x) \in F\) is of the form \(g(x)=X_0(x)+k(x)\varPi \) with \(\deg (g) \le {\sum \nolimits _{i=1}^{t} {d_i}}-1\). Therefore, one choice for k(x) corresponds to one choice for \(g(x) \in F\). Since \(\deg (X_0) < \deg (\varPi )\), \(\deg (g) = \deg (k)+\deg (\varPi )\). Therefore, \(\deg (k) \le {\sum \nolimits _{i=1}^{t} {d_i}}-1-\deg (\varPi )\). That is, \(\deg (k) \le \delta -1\). Therefore, the number of choices for k(x) is \(p^\delta \). Hence, \(|{F}| = p^\delta \). \(\Box \)
From Theorem 10, we can see that \(t-1\) parties would know that the dealer must have selected one of the \(p^\delta \) polynomials in F. And the probability that each polynomial is selected by the dealer is the same by Theorem 9.
Next, we study how these polynomials in F, modulo \(m_0(x)=x^{d_0}\), map to the secret s(x) to find out the conditional probability distribution of s(x) regarded as a random variable.
Theorem 11
Let
For any \(s(x) \in \mathcal {S}\), let
Then, the following proposition holds.
Proof
For any fixed \(s(x) \in \mathcal {S}\), since \(\psi ^{-1}(s(x)) \subseteq F\), elements of \(\psi ^{-1}(s(x))\) is of the form \(X_0(x)+k(x)\varPi \) with \(\deg (k) \le \delta \) such that
Therefore, to count the number of elements in \(\psi ^{-1}(s(x))\) is to count how many k(x) with \(\deg (k) \le \delta -1\) satisfy Expression 12.
Subtracting \(X_0(x)\) through Expression 12, we have
Since \(m_0(x)\) and \(\varPi \) are coprime in our scheme, \(\varPi \) has a multiplicative inverse modulo \(m_0(x)\), then,
Let \(k_0(x) = (s(x)-X_0(x))\varPi ^{-1} \bmod m_0(x)\). Then, any k(x) satisfying Expression 12 is of the form \(k(x)=k_0(x) + n(x)m_0(x)\) with \(n(x) \in {\mathbb {F}_{p}} [x]\). Since \(\deg (k_0) < \deg (m_0)\), \(\deg (k) = \deg (n) + \deg (m_0)\). In addition, \(\deg (k) \le \delta - 1\), \(\deg (n) \le \delta - d_0 - 1\). Therefore, the number of such satisfiable n(x) is \(p^{\delta -d_0}\). Hence, \(|{\psi ^{-1}(s(x))}| = p^{\delta -d_0}\) is a constant. \( \Box \)
So far, we have the foundation to discuss the conditional probability distribution of s(x) under the condition that \(t-1\) shares are known. It’s clear that \(t-1\) parties knowing \(X_0(x)\) can determine the set F of all possible randomly selected f(x), by Theorem 10, \(|{F}| = p^\delta \). Over all the \(p^\delta \) choices, by Theorem 11, only \(p^{\delta -d_0}\) choices lead to the correct secret. Therefore, the conditional probability that \(t-1\) parties can guess out the secret is \(\frac{p^{\delta -d_0}}{p^\delta } = \frac{1}{p^{d_0}}\). That is,
This implies that our scheme is perfect in security.
3.3 Information Rate
In this subsection, we discuss the information rate of our newly proposed scheme. In our scheme, the secret is a polynomial of degree at most \(d_0-1\) and it takes \(d_0\) elements in \( {\mathbb {F}_{p}} \) to represent the secret. On the other hand, the n-th party holds the largest share which is a polynomial of degree at most \(d_n-1\) and consists of \(d_n\) elements in \( {\mathbb {F}_{p}} \). Therefore, the information rate of our threshold scheme is \(\frac{d_0}{d_n}\).
Note that our scheme does not require \(d_0 < d_n\), instead, the dealer can select the modulus polynomials with the identical degree, i.e.,
In this case, the information rate is 1 and our scheme is an ideal one. By Theorem 7, we know that Expression 13 can be easily satisfied in practice and Algorithm 2 provides an efficient way.
3.4 Comparison
In this subsection, we compare our scheme with Asmuth-Bloom’s scheme and Shamir’s scheme. We show that our scheme has its advantage in some aspects, which encourages us to consider our scheme as a good base when designing new secret sharing schemes.
We start with the comparison with Asmuth-Bloom’s scheme and our scheme enjoys the advantages in
-
Perfectness and Information rate: From Subsect. 2.5, we know that Asmuth-Bloom’s is neither perfect nor ideal. However, in Subsect. 3.2, we have shown that our scheme is perfect and in Subsect. 3.3, we have discussed that our scheme can reach information rate 1. Although, [28] has shown that Asmuth-Bloom’s scheme is asymptotically ideal, it takes moduli of huge size to achieve this asymptotic property, which is not practical at all.
-
Simplicity: During the construction of our scheme, the dealer only needs to find n distinct irreducible polynomials of degree \(d_0\) with Algorithm 2 and these polynomials automatically satisfy the required conditions (Expressions 6, 7 and 8) of our scheme. However, Asmuth-Bloom’s scheme failed to give an explicit way to find its moduli and to our knowledge, there is no such specialized algorithm. One candidate may be selecting consecutive prime numbers. But when the prime numbers are small, such consecutive prime numbers are not guaranteed to satisfy the required Expression 5. When the prime numbers are large, Expression 5 may be easier to satisfy, but it would be impractical if the number of secrets is small.
-
Computing efficiency in certain cases: First, different from public key cryptosystems, where the private key related with the security level is usually large, the secret sharing schemes mentioned in this paper does not put its base on some intractable problem. Therefore, we usually do not put a restriction on the parameters related with security, but the parameters are determined considering both security level and practical needs. Now, suppose we are in the situation where we want to share a secret of huge size, e.g., a 2048 or larger bits key for the RSA cryptosystem, with Asmuth-Bloom’s scheme, we may need to find prime moduli of this size (larger than \(2^{2048}\)). However, it suffers from the fact that
-
to find a prime number or test the primality of numbers of such size takes a long time,
-
and the basic operations on numbers of such size is also time-consuming.
In contrast, using our scheme with a proper \(d_0\) selected (say \(d_0=64\)), a prime number around \(2^{32}\) will handle this case without extremely huge numbers involved, thus, required computation can be completed efficiently. Another situation is when the secret can be expressed as a \(d_0\) bit number. Then, by working in \( {\mathbb {F}_{2}} [x]\), polynomial operations of our scheme can be implemented with bitwise operations to speed up.
-
When it comes to the comparison with Shamir’s scheme, the above-mentioned advantages fade. Since Shamir’s scheme is already ideal, our scheme can only draw with Shamir’s scheme in perfectness and information rate. Shamir’s scheme is also easy to construct, since the dealer only needs to find one prime number and the rest steps are clear. As for the last point, Shamir’s scheme can also naturally work in the finite field of \(p^n\) elements to deal with the situation when the secret is of huge size and in the finite field of \(2^{d_0}\) elements to enjoy the speed up of bitwise operations. Therefore, in all the aspects discussed, we can only say that our scheme draws with Shamir’s scheme.
However, the important difference between Shamir’s scheme and our scheme is that our scheme still preserves the structure of the CRT as Asmuth-Bloom’s scheme does. That is,
-
in Shamir’s scheme, all parties are equal,
-
while in our scheme, different parties can be easily assigned shares of different size to be distinguished from each other. Therefore, our scheme is more flexible than Shamir’s scheme.
This may also be the reason why Asmuth-Bloom’s scheme is significant even though Shamir’s scheme behaves better than Asmuth-Bloom’s scheme in perfectness, information rate and computing efficiency. In practice, schemes based on Asmuth-Bloom’s scheme mostly take advantages of the property of CRT. For example,
-
In the weighted scheme of [15], parties with larger weights are assigned larger moduli while parties with smaller weights are assigned smaller moduli. This can be easily achieved by the property of CRT.
-
In the multilevel threshold scheme of [16], parties in different security levels are assigned moduli of different size to ensure different threshold for each level.
4 Shamir’s Scheme as a Special Case of Our Scheme
As we know, Lagrange interpolation is closely related to CRT over polynomial ring [7].
In this section, we show that Shamir’s scheme can be regarded as a special case of our scheme, indicating that Shamir’s scheme, Asmuth-Bloom’s scheme and our scheme are all tightly connected in essence.
To derive Shamir’s scheme, we can select the parameters of our proposed scheme as follows.
-
p is still a prime number
-
let \(d_0=1\) and \(m_0(x)=x \in {\mathbb {F}_{p}} [x]\)
-
for all \(i \in [n]\) let \(m_i(x) = x-a_i \in {\mathbb {F}_{p}} [x]\) such that
$$\begin{aligned} \forall j, l \in [n], j \ne l \implies a_j \ne a_l \end{aligned}$$ -
let \(s(x)=a_0 \in {\mathbb {F}_{p}} [x]\)
-
let \(\alpha (x)\) be a random polynomial in \( \{ {g(x) \in {\mathbb {F}_{p}} [x]} \mid {\deg (g(x)) \le t-2.} \} \)
It is easy to check that the above selection of parameters satisfies all the required conditions of our scheme. Then, \(f(x)=s(x)+\alpha (x)m_0(x)=a_0+\alpha (x)x\) is a random polynomial of degree at most \(t-1\) and the secret is exactly \(s(x)=a_0=f(0)\), which coincides with Shamir’s scheme. The share for the i-th party would be \(s_i(x)=(f(x) \bmod m_i(x)) = (f(x) \bmod (x-a_i)) = f(a_i)\), which also coincides with Shamir’s scheme.
To see that \(f(x) \pmod {x-a_i} = f(a_i)\), just divide f(x) with \(x-a_i\) and get \(f(x)=(x-a_i)q(x)+r\) for some unique \(q(x), r \in {\mathbb {F}_{p}} [x]\) with \(\deg (r) < \deg (x-a_1)=1\). Therefore, r is actually a constant in \( {\mathbb {F}_{p}} [x]\). Then, replacing x with \(a_i\) in both side will result in \(f(a_i)=r\), that is, \(f(x) \pmod {x-a_i} = f(a_i)\).
In the secret reconstruction phase, for brevity of symbols, suppose t parties \(\{ 1,2, \dots , t \}\) want to recover the secret. Pooling their shares together, they have the following system of congruences
Let
For all \(i \in [t]\), since
and \(\gcd (M_i(x), x-a_i)=1\), we have
Therefore, by Theorem 4, the solution of Expression 14 can be written as
which coincides with the Lagrange interpolation polynomial for recovering the secret in Shamir’s scheme.
5 A Weighted Threshold Secret Sharing Scheme
In this section, we propose a weighted secret sharing scheme based on our threshold scheme in Subsect. 3.1. The weighted scheme can also be seen as a counterpart of the scheme based on Asmuth-Bloom’s scheme [15] for the polynomial ring over a finite field. By this weighted scheme, we illustrate that our scheme can serve as a better substitution for Asmuth-Bloom’s scheme. Also, we recommend our threshold scheme for users who need some CRT based scheme as a base in the future. In Subsect. 5.1, we describe the weighted scheme. Then, in Subsect. 5.2, we discuss its security, information rate and comparison.
5.1 The Weighted Threshold Scheme
As is in Subsect. 2.4, the access structure realized by a \((t, n, \omega )\)-weighted threshold secret sharing scheme is of the form
where \(\omega \) is the weight function evaluated over \(\mathbb {Z}\). For simplicity of notations, let \(w_i = \omega (i)\) for all \(i \in [n]\) and assume that
Share Distribution: The dealer chooses a prime p and pairwise coprime polynomials \(m_0(x)=x, m_1(x), \dots , m_n(x) \in {\mathbb {F}_{p}} [x]\). Let
The chosen polynomials must satisfy the condition that \(\forall i \in [n], d_i=w_i\). The secret space is \( {\mathbb {F}_{p}} \). Suppose that the dealer has picked his secret \(s \in {\mathbb {F}_{p}} \). Then, the dealer randomly chooses a polynomial \(\alpha (x)\) from the set
That is, \(\alpha (x)\) is a polynomial of degree at most \(t-2\). Next, the dealer computes \(f(x)=s+\alpha (x)m_0(x)=s+\alpha (x)x\). Let \(d_f=\deg (f(x))\) and \(d_\alpha =\deg (\alpha (x))\). It is clear that
Finally, the dealer computes
as the share of the i-th party and sends \(s_i(x)\) privately to the i-th party.
Secret Reconstruction: If k parties \(\{ i_1, \dots , i_k \} \subseteq [n]\) with
want to reconstruct the secret, they pool their private shares together and form the following system of congruences
They can solve this system of congruences and get a solution \(X_0(x) \in {\mathbb {F}_{p}} [x]\). By the CRT for polynomial rings over a field (Theorem 3), the solution is unique if only polynomials of degree less than \({\sum \nolimits _{j=1}^{k} {d_{i_j}}}\) are considered. Since
and f(x) also is a solution of the above system of congruences, they have \(f(x)=X_0(x)\). Then, the secret can be recovered by computing
5.2 Discussion of the Weighted Threshold Scheme
Since our weighted scheme can also be seen as a parameterization of our threshold scheme, we only briefly discuss the security and information rate of our weighted scheme in this subsection. Then, we compare it with the existing weighted scheme.
First, as a fundamental criterion, our weighted threshold scheme is perfect. This conclusion should be clear since the weighted scheme can be seen as a parameterization of our threshold scheme, except that, in the weighted scheme, one party with weight w is thought of as equivalent with w parties in the threshold scheme.
In our weighted scheme, the secret ranges over \( {\mathbb {F}_{p}} \) while the largest share is the polynomial of degree \(w_n-1\) which consists of \(w_n\) coefficients in \( {\mathbb {F}_{p}} \). Therefore, the information rate is \(\frac{1}{w_n}\).
To our knowledge, there are several existing weighted threshold schemes based on the CRT for integers, like [21, 35] and [15]. In [15], it is commented that
-
Both schemes of [21] and [35] are not perfect while [15] is perfect.
-
In the scheme of [21], the dealer needs to find out all minimal subsets of authorized access structure and then determines the modulus of each shareholder accordingly and it is a time-consuming process.
-
The size of the CRT moduli and private shares of [15] is smaller than the moduli of [21] and [35].
Still, compared with the scheme of [15], our weighted scheme enjoys the following advantages in
-
Information rate: Our information rate is \(\frac{1}{w_n}\) while the information rate of the scheme of [15] is less than \(\frac{1}{w_n}\).
-
Simplicity: In the scheme of [15], the constraint on the modulus for each party is stricter than that in Asmuth-Bloom’s scheme. As mentioned in Subsect. 3.4, to find such a series of moduli is not trivial and there’s no specialized algorithm. But it is simpler to find the moduli of our scheme with Algorithm 2.
-
Computing efficiency: Our weighted scheme still inherits the advantage of the computing efficiency in certain cases over the scheme based on the CRT for integers as mentioned in Subsect. 3.4.
6 Conclusion
Currently, existing CRT based (t, n)-threshold SS schemes are not ideal. Compared with Shamir’s scheme, they have a lower information rate and are harder to construct. In this paper, we present the generalized (t, n)-threshold SS scheme based on the CRT for the ring of polynomials over a finite field. In particular, our scheme is perfect in security and has information rate 1. Moreover, we showed that Shamir’s scheme is a special case of our threshold scheme and thus establish the connection among Shamir’s scheme, Asmuth-Bloom’s scheme and our proposed scheme. Finally, we present a weighted threshold scheme based on our threshold scheme. Comparison shows that our weighted scheme has great advantages over existing schemes based on Asmuth-Bloom’s scheme, which enables our scheme to be a better substitution for Asmuth-Bloom’s scheme.
Change history
03 February 2021
Two references to papers by T. Galibus et al. have been added to this paper because these publications, published in 2007 and 2008, contain results mentioned in the present paper. The authors of the present paper were unaware of these publications and obtained their results independently.
References
Asmuth, C., Bloom, J.: A modular approach to key safeguarding. IEEE Trans. Inf. Theor. 29(2), 208–210 (1983)
Beimel, A.: Secret-sharing schemes: a survey. In: Chee, Y.M., et al. (eds.) IWCC 2011. LNCS, vol. 6639, pp. 11–46. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-20901-7_2
Ben-Or, M., Goldwasser, S., Wigderson, A.: Completeness theorems for non-cryptographic fault-tolerant distributed computation. In: Proceedings of the Twentieth Annual ACM Symposium On Theory Of Computing, pp. 1–10. ACM (1988)
Blakley, G.R., et al.: Safeguarding cryptographic keys. In: Proceedings of the National Computer Conference, vol. 48, pp. 313–317 (1979)
Brickell, E.F.: Some ideal secret sharing schemes. In: Quisquater, J.-J., Vandewalle, J. (eds.) EUROCRYPT 1989. LNCS, vol. 434, pp. 468–475. Springer, Heidelberg (1990). https://doi.org/10.1007/3-540-46885-4_45
Capocelli, R.M., De Santis, A., Gargano, L., Vaccaro, U.: On the size of shares for secret sharing schemes. J. Cryptol. 6(3), 157–167 (1993)
Childs, L.N.: A Concrete Introduction to Higher Algebra. UTM. Springer, New York (2009). https://doi.org/10.1007/978-0-387-74725-5
Cohen, H.: A Course in Algorithmic Algebraic Number Theory, vol. 138. Springer, Heidelberg (1993). https://doi.org/10.1007/978-3-662-02945-9
Cramer, R., Damgård, I., Maurer, U.: General secure multi-party computation from any linear secret-sharing scheme. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 316–334. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_22
Fuyou, M., Yan, X., Xingfu, W., Badawy, M.: Randomized component and its application to (\( t \), \( m \), \( n \))-group oriented secret sharing. IEEE Trans. Inf. Forensics Secur. 10(5), 889–899 (2015)
Galibus, T., Matveev, G.: Generalized mignotte’s sequences over polynomial rings. Electron. Notes Theor. Comput. Sci. 186, 43–48 (2007). https://doi.org/10.1016/j.entcs.2006.12.044
Galibus, T., Matveev, G., Shenets, N.: Some structural and security properties of the modular secret sharing. In: 10th International Symposium on Symbolic and Numeric Algorithms for Scientific Computing, pp. 197–200. IEEE Press, New York (2008). https://doi.org/10.1109/SYNASC.2008.14
Gennaro, R., Rabin, M.O., Rabin, T.: Simplified VSS and fast-track multiparty computations with applications to threshold cryptography. In: Proceedings of the Seventeenth Annual ACM Symposium on Principles Of Distributed Computing, pp. 101–111. ACM (1998)
Goldreich, O., Ron, D., Sudan, M.: Chinese remaindering with errors. In: Proceedings of the Thirty-first Annual ACM Symposium on Theory of Computing, pp. 225–234. ACM (1999)
Harn, L., Fuyou, M.: Weighted secret sharing based on the Chinese remainder theorem. Int. Netw. Secur., 1–7 (2013)
Harn, L., Fuyou, M.: Multilevel threshold secret sharing based on the Chinese remainder theorem. Inf. Process. Lett. 114(9), 504–509 (2014)
Harn, L., Fuyou, M., Chang, C.C.: Verifiable secret sharing based on the chinese remainder theorem. Secur. Commun. Netw. 7(6), 950–957 (2014)
Harn, L., Hsu, C., Zhang, M., He, T., Zhang, M.: Realizing secret sharing with general access structure. Inf. Sci. 367, 209–220 (2016)
Harn, L., Lin, C.: Strong (n, t, n) verifiable secret sharing scheme. Inf. Sci. 180(16), 3059–3064 (2010)
Iftene, S.: Secret sharing schemes with applications in security protocols. Sci. Ann. Cuza Univ. 16, 63–96 (2006)
Iftene, S., Boureanu, I.C.: Weighted threshold secret sharing based on the Chinese remainder theorem. Sci. Ann. Cuza Univ. 15(EPFL–ARTICLE–174320), 161–172 (2005)
Kaya, K., Selçuk, A.A.: Threshold cryptography based on Asmuth-Bloom secret sharing. Inf. Sci. 177(19), 4148–4160 (2007)
Lang, S.: Algebra. Graduate Texts in Mathematics, vol. 211, 3rd edn. Springer, New York (2002). https://doi.org/10.1007/978-1-4613-0041-0. 1. ALL-ALL
Liu, Y., Harn, L., Chang, C.C.: A novel verifiable secret sharing mechanism using theory of numbers and a method for sharing secrets. Int. J. Commun. Syst. 28(7), 1282–1292 (2015)
Mignotte, M.: How to share a secret. In: Beth, Thomas (ed.) EUROCRYPT 1982. LNCS, vol. 149, pp. 371–375. Springer, Heidelberg (1983). https://doi.org/10.1007/3-540-39466-4_27
Morillo, P., Padró, C., Sáez, G., Villar, J.L.: Weighted threshold secret sharing schemes. Inf. Process. Lett. 70(5), 211–216 (1999)
Pang, L.J., Wang, Y.M.: A new (t, n) multi-secret sharing scheme based on Shamir’s secret sharing. Appl. Math. Comput. 167(2), 840–848 (2005)
Quisquater, M., Preneel, B., Vandewalle, J.: On the security of the threshold scheme based on the Chinese remainder theorem. In: Naccache, D., Paillier, P. (eds.) PKC 2002. LNCS, vol. 2274, pp. 199–210. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45664-3_14
Shamir, A.: How to share a secret. Commun. ACM 22(11), 612–613 (1979)
Shankar, B., Srinathan, K., Rangan, C.P.: Alternative protocols for generalized oblivious transfer. In: Rao, S., Chatterjee, M., Jayanti, P., Murthy, C.S.R., Saha, S.K. (eds.) ICDCN 2008. LNCS, vol. 4904, pp. 304–309. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-77444-0_31
Shoup, V.: A computational Introduction to Number Theory and Algebra. Cambridge University Press, Cambridge (2009)
Stinson, D.R.: An explication of secret sharing schemes. Des. Codes Cryptogr. 2(4), 357–390 (1992)
Tassa, T.: Generalized oblivious transfer by secret sharing. Des. Codes Cryptogr. 58(1), 11–21 (2011)
Yang, C.C., Chang, T.Y., Hwang, M.S.: A (t, n) multi-secret sharing scheme. Appl. Math. Comput. 151(2), 483–490 (2004)
Zou, X., Maino, F., Bertino, E., Sui, Y., Wang, K., Li, F.: A new approach to weighted multi-secret sharing. In: 2011 Proceedings of 20th International Conference on Computer Communications and Networks, ICCCN, pp. 1–6. IEEE (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Ning, Y., Miao, F., Huang, W., Meng, K., Xiong, Y., Wang, X. (2018). Constructing Ideal Secret Sharing Schemes Based on Chinese Remainder Theorem. In: Peyrin, T., Galbraith, S. (eds) Advances in Cryptology – ASIACRYPT 2018. ASIACRYPT 2018. Lecture Notes in Computer Science(), vol 11274. Springer, Cham. https://doi.org/10.1007/978-3-030-03332-3_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-03332-3_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03331-6
Online ISBN: 978-3-030-03332-3
eBook Packages: Computer ScienceComputer Science (R0)




 denotes the principal ideal generated by a. Also,
denotes the principal ideal generated by a. Also, 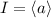 is a principal ideal for some
is a principal ideal for some 