Abstract
Conditional face synthesis has been an appealing yet challenging problem in computer vision. It has a wide range of applications. However, few works attempt to leverage the synthesized face images for data augmentation and improve performance of recognition model. In this paper, we propose a conditional face synthesis framework that combines a variational auto-encoder with a conditional generative adversarial network, for synthesizing face images with specific identity. Our approach has three novel aspects. First, we propose to leverage the synthesized face images to do data augmentation and train a better recognition model. Second, we adopt multi-scale discriminators to enable high-quality image generation. Third, we adopt identity-preserving loss and classification loss to ensure identity invariance of synthesized images, and use feature matching loss to stabilize the GAN training. With extensive qualitative and quantitative evaluation, we demonstrate that face images generated by our approach are realistic, discriminative and diverse. We further show that our approach can be used for data augmentation and train superior face recognition models.
X. Xie—This project is supported by the Natural Science Foundation of China (61702566, 61672544) and Tip-top Scientific and Technical Innovative Youth Talents of Guangdong special support program (No. 2016TQ03X263).
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Since deep learning is data-driven methods, ample data have been utilized to train high performance models in various computer vision tasks, such as image classification [14], face recognition [20] and so on. However, There are many realistic scenarios which limit data are available. The deep neural networks is prone to overfit in the training set and yield pool generalization ability.
As a generative problem in computer vision, image synthesis is appealing yet challenging. In the past few years, it has received great research interests and has a wide range of applications, such as image generation [3], face attribute editing [5], image translation [19], face completion [4], image super-resolution [15] among others. However, exist works seldom utilize the synthesized images for further recognition or detection tasks, like face recognition. In this work, we propose to leverage the synthesized face images for data augmentation and improve performance of recognition model.
Traditional data augmentation techniques [14], like translation, rotation, horizontal flip and random crop, can introduce some known intra-class variance. These techniques are proved to be valid, but the transformations are limit and constant. We argue that we can learn a generative model to do data augmentation. Through a trained model, we can generate images with more abundant intra-class variance.
This work mainly focuses on conditional face synthesis, i.e., given an identity label and a randomly sampled latent vector, generating face images with specific identity, as illustrated in Fig. 1. We hope that synthesized face image have following characteristics: (1) Images are photo-realistic, diverse and rich in intra-class variance, such as pose, illumination and expression. (2) Images must preserve identity so that they can be used for face recognition.
Inspired by CVAE-GAN [3], we propose a conditional face synthesis framework that combines a variational auto-encoder with a conditional generative adversarial network, for synthesizing face images with specific identity. However, we find that using traditional discriminator structure and adversarial loss function will lead to many problems. First, the GAN training is unstable because of the gradient vanishing problem. Then the quality of synthesized face images are poor. Moreover, synthesized images are easy to loss identity information which is the key for recognition task. To tackle these problems, we first adopt multi-scale discriminators [19] to enable high-quality image generation. Specifically, we use multiple discriminators that have the same network structure but handle different image scales to improve image quality. Second, we adopt identity-preserving loss and classification loss to ensure identity invariance of synthesized images. Third, we use feature matching loss to stabilize the GAN training.
In summary, This paper makes the following contributions.
-
1.
We propose a conditional face synthesis framework that combines a variational auto-encoder with a conditional generative adversarial network, for synthesizing face images with specific identity. Furthermore, we leverage the synthesized face images to do data augmentation and train a better recognition model.
-
2.
We adopt multi-scale discriminators to enable high-quality image generation, adopt identity-preserving loss and classification loss to ensure identity invariance of synthesized images, and use feature matching loss to stabilize the GAN training.
-
3.
With extensive qualitative and quantitative evaluation, we demonstrate that face images generated by our approach are realistic, discriminative and diverse. Furthermore, we show that our approach can be used for data augmentation and train superior face recognition models.
2 Related Work
In the last few years, deep generative models have made significant breakthroughs in face synthesis. Since deep neural network is able to learn powerful feature representations, These methods can capture complex data distributions and generate more realistic images than traditional methods. The mainstream face generative models can be roughly divided into two categories: Variational Auto-encoder (VAE) [6] and Generative Adversarial Network (GAN) [2, 3, 7, 11, 19].
Variational Auto-encoder (VAE) [6] is one of the most popular approaches to unsupervised learning of complicated distributions. It is actually a pair of connected networks: an encoder and a decoder/generator. The encoder maps an input image to a latent representation, and the decoder/generator converts it back to the original input. With the reparameterization trick [6], VAE is able to be optimized using stochastic gradient descent. However, since VAE uses l2 loss or l1 loss as reconstruction loss, the images generated by VAE often suffer from fuzzy effect.
Generative Adversarial Network (GAN) has attracted significant attention on the research of deep generative models [2, 3, 7, 11, 19]. GAN consists of a discriminator D and a generator G that D and G compete in a minimax two-player game. Huang et al. [11] proposed a Two-Pathway Generative Adversarial Network (TP-GAN) for synthesising photorealistic frontal view face from profile. This work perceives global structures and local details simultaneously. To improve the quality of generated images, Wang et al. [19] adopted multi-scale generator and discriminator architectures, as well as improved adversarial loss. Arjovsky et al. [2] adopted Earth Mover Distance to measure the similarity between two distributions, which stabilize the GAN training and alleviate mode-collapse phenomenon to a certain extent.
Bao et al. [3] presents variational generative adversarial networks (CVAE-GAN) for synthesizing images in fine-grained categories. Their work is related to our work. But compared with their method, our method has the following differences: (1) We introduce identity-preserving loss to ensure identity invariance of synthesized images. (2) We adopt multi-scale and multi-task discriminators to enable high-quality image generation.
3 Approach
In this section, we first review the vanilla generative adversarial network (Sect. 3.1). Then we introduce the overall of our conditional face synthesis framework (Sect. 3.2). Next, we describe the detailed network architecture of our method (Sect. 3.3). Finally, we introduce the object functions of the proposed method and the training pipeline (Sect. 3.4).
3.1 Generative Adversarial Network
Generative Adversarial Network (GAN) consists of a discriminator D and a generator G that D and G compete in a minimax two-player game. Specifically, a discriminator D tries to distinguish a real image from a synthesized one, while a generator G tries to capture the data distribution and generate images that can fool D. Specifically, D and G play the following two-player minimax game with value function V(D, G):
3.2 Problem Formulation
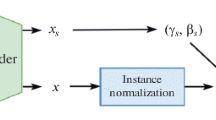
In this section, we elaborate the proposed conditional face synthesis framework. Given an identity label c and a randomly sampled latent vector z, our goal is to generate face images with specific identity. The overall framework is visualized in Fig. 2. Our method consists of four components: (1) encoder network E, (2) generative network G, (3) discriminative network D, (4) identity-preserving network FR. Next, we introduce the function of each component.
The encoder network E is similar to the encoder of VAE. By learning a distribution P(z|x), E first maps the image x to the mean and covariance, and then obtains the latent representation z by reparameterization trick [6]. The generative network G is similar to the generator of conditional GAN [16]. By learning a distribution P(x|z, c), G generates a image G(z, c) given a identity label c and a randomly sampled latent vector z. Specifically, The latent representation \(z_{encode}\) is obtained from E and the latent representation \(z_{random}\) is sampled from normal gaussian distribution. The generated images are \(x_{encode}\) and \(x_{random}\), respectively. Different from the traditional discriminator, we adopt multi-task learning for discriminative network D. D distinguishes real/fake faces and performs identity classification, i.e., estimate the posterior P(c|x), simultaneously. In order to leverage synthesized face images for face recognition task, it is crucial to keep the identity invariance of synthesized images. We thus introduce an identity-preserving network FR to ensure identity invariance through feature matching manner.
3.3 Network Architecture
The encoder network E consists of four residual blocks with 2x downsampling. The architecture of residual block is shown in Fig. 3. The generative network G consists of 6 deconvolution layers with 2x upsampling.
The discriminative network D consists of six convolution layers with 2x downsampling. Different from traditional GAN that the discriminator only distinguishes real/fake images, we adopt multi-task learning for D. D distinguishes real/fake faces and performs identity classification simultaneously. Specifically, our discriminator produces two probability distributions, i.e., \(D:x\rightarrow \{D_{src}(x),D_{cls}(x)\}\), where \(D_{src}(x)\) is the probability that discriminator regards the input as true, and \(D_{cls}(x)\) is the posterior for identity classification.
The architecture of residual block [23].
Recent work [19] shows that the discriminator needs a large receptive field to produce a high-quality image. Inspired by [19], we introduce multi-scale discriminators to distinguish real/fake images from different scales. As illustrated in Fig. 4, we use two discriminators \(D^1\) and \(D^2\). Each has the same network structure but handle images from different scales. The discriminator with coarse scale has large receptive field, which helps to keel global structure information. The discriminator with fine scale has small receptive field, which helps to produce details.
3.4 Object Function
The object function used in our approach is a weighted sum of five individual loss functions. Next, we will describe each loss function, respectively.
Adversarial Loss. Traditional GAN uses cross entropy as adversarial loss. Actually at the early stage of training, the distributions of real/fake images may not overlap with each other. So it is easy for D to distinguish real/fake images. This leads to gradient vanishing problem [1]. To stabilize the training process, we use Wasserstein GAN with gradient penalty [2, 8] as adversarial loss. It takes the form:
where \(D_{src}^k(\cdot )\) denotes the output probability from k-th discriminator. \(\hat{x}\) is the linear interpolation between real and fake samples. \(\lambda _{gp}\) is the weight of gradient penalty and we use \(\lambda _{gp}=1.0\) for all experiments.
Feature Match Loss. To stabilize the GAN training, we adopt feature match loss to train generator. Specifically, the feature match loss tries to minimize the distance of intermediate features from multi-scale discriminators between real and fake images. We denote the i-th layer feature of k-th discriminator as \(D_{(i)}^k\). The feature match loss is defined as follows:
where T is the number of layers used for feature matching. \(N_i\) is the number of elements in i-th layer. Here we use features of the last three convolution layers.
Pixel Reconstruction Loss. When passing an input image x through E and G, we can get a generated img \(G(z_{encode},c)\). We hope that \(G(z_{encode},c)\) can reconstruct the input x as far as possible. Hence, we adopt pixel-wise L1 loss to maintain structure information:
In addition, the encoder network E maps input x to the mean(\(\mu \)) and covariance(\(\epsilon \)). We apply KL loss to ensure that the latent representation obeys normal gaussian distribution:
Classification Loss. For an arbitrary face image, we hope D can not only distinguish real/fake, but also predict the identity. In detail, the classification loss is defined as
where \(D_{cls}^k(c|x)\) represents the posterior for identity classification from k-th discriminator. By minimizing this objective, D tries to classify a real image to its corresponding identity, and G tries to generate a image with specific identity.
Identity-Preserving Loss. In order to leverage synthesized face images for face recognition task, it is crucial to keep the identity invariance of synthesized images. We imitate the perceptual loss [12] widely used in image style transfer. Specifically, with a pre-trained face recognition model Light CNN9 [20], we learn to match the intermediate features between real and fake images that have the same identity. The identity-preserving loss is calculated as follows:
where \(FR(\cdot )\) is the output of penultimate fc layer of Light CNN9. Since Light CNN9 is dedicated to face recognition, its intermediate features contain rich identity information. So it’s reasonable to keep identity invariance by such feature matching manner. During the training process, we freeze the parameters of Light CNN9 and only propagate the gradients back to E and G. We note that a similar loss is used in [11].
Overall Object Function. Finally, the overall object function is a weighted sum of loss functions defined above:
where \(\lambda _{cls},\lambda _{FM},\lambda _{pixel},\lambda _{KL},\lambda _{id}\) are hyper-parameters to control the importance of each loss. We use \(\lambda _{cls}=1,\lambda _{FM}=1,\lambda _{pixel}=10,\lambda _{KL}=0.01,\lambda _{id}=1\) for all experiments. The whole training pipeline is shown in Algorithm 1.

4 Experiments
To validate the effectiveness of our approach, we evaluate our model qualitatively and quantitatively on FaceScrub [17] and LFW [9] datasets. We train our model on FaceScrub and test the model on LFW.
At preprocess stage, we perform face detection and get the facial landmarks using the multi-task cascaded CNN [22]. Then we align the faces by similarity transformation based on facial landmarks. The sizes of real and synthesized images are 128 \(\times \) 128. All the input are horizontal flip randomly.
For E and G, we use ReLU as activation function. The instance normalization is applied after each convolution layer. For multi-scale discriminators, we use two discriminators \(D^1\) and \(D^2\), where the input of \(D^1\) is 128 \(\times \) 128, and the input of \(D^2\) is 64 \(\times \) 64. We use Leaky ReLU (\(\lambda =0.01\)) as activation function.
In our experiments, the dimension of latent representation is 256. Our model is implemented using deep learning framework pytorch. The models are optimized using Adam [13] with \(\beta _1=0.5\) and \(\beta _2=0.999\). We train all models with a learning rate of 0.0002 for the first 100 epochs and linearly decay the learning rate to 0 over the next 100 epochs. Training takes about 36 h on four NVIDIA 1080Ti GPU.
4.1 Qualitative Evaluation
Visualization Comparison. In this section, we compare the proposed method with CVAE and CGAN qualitatively. For CVAE, we remove the discriminative network D and only keep the pixel reconstruction loss \(\mathcal {L}_{pixel}\) and KL loss \(\mathcal {L}_{KL}\). For CGAN, we remove the encoder network E as well as the pixel reconstruction loss and KL loss, i.e., set \(\lambda _{pixel}\) and \(\lambda _{KL}\) as 0. For fair comparison, we use the same network structure and training data. All methods use G to generate images.
At test stage, we first randomly sample a identity c and a latent vector \(z\sim N(0,I)\), and then pass them through G to generate a image with identity c. The visualization results of each method are shown in Fig. 5. We can see that images generated by CVAE are very blur. The reason is that CVAE merely uses the l1 reconstruction loss. Then images generated by CGAN often loss structure information in some regions, which is because of the absence of encoder. On the contrary, images generated by our approach are realistic and contain abundant intra-class variance, such as pose and expression. Furthermore, our method can keep the identity well. This shows the effectiveness of our approach.
Latent Representation Interpolation. To validate that our method can learn continuous and general latent space, we perform interpolation for latent representation. Specifically, we first randomly choose two faces of the same identity \(x_1\) and \(x_2\), and then get latent vectors \(z_1\) and \(z_2\) through encoder network E. Next, we obtain a series of latent vectors by linear interpolation, i.e., \(z=\alpha z_1+(1-\alpha )z_2,\alpha \in [0,1]\). Finally, we generate samples using these interpolated vectors, as shown in Fig. 6. At each row, the left and right side are \(x_1\) and \(x_2\), respectively. The interpolation results are in the middle. It can be seen that the facial pose, expression and skin color change gradually from left to right, which shows that the latent space learnt by our model is continuous.
4.2 Quantitative Evaluation
Evaluating the performance of generative model is a challenging problem. Many existing methods in face synthesis evaluate images by human, which is a laborious work and lack of objectivity. Following [3], we evaluate the model on image discriminability, realism and diversity.
We first randomly generate 53k face images (100 images for each identity) using our method, CVAE and CGAN, respectively. To validate the discriminability of generated images, we train a face classification model using real data. Here we choose Light CNN29 [20] as a basic model, whose structure is similar to Light CNN9 but deeper than it. With the pre-trained classification model, we calculate the top-1 accuracy of images generated by each method. Table 1 shows the results. Since CVAE merely uses the l1 reconstruction loss. It can’t ensure identity invariance. So the accuracy is very poor. Our method achieve the best top-1 accuracy, showing significant margin than CVAE and is closing to real data (99.56% vs 99.69%). This suggests that images generated by our method is discriminative. It can be noted that CGAN also achieve high accuracy. We guess it’s the contribution of identity-preserving loss. To validate this assumption, We remove the identity-preserving loss (set \(\lambda _{id}\) as 0), and retrain the model. We find that the accuracy drops dramatically (from 99.56% to 79.50%), which demonstrates that the identity-preserving loss plays a crucial role in keeping identity information.
We adopt inception score [18] to evaluate the realism and diversity of generated images. Specifically, we first train a face recognition model on CASIA-Webface [21] dataset, and then use \(exp(E_xKL(p(y|x)\Vert p(y)))\) as metric. If the model can generate more photo-realistic and diverse images, the inception score will be higher. From Table 1 we can see that our method achieve the highest score and is closing to the real data.
4.3 Data Augmentation
The ultimate goal of this paper is to utilize generated images to train better face recognition models. In this section, we further demonstrate that our method can be used for data augmentation. We use FaceScrub as training set and LFW as testing set.
Following [3], we exploit two data augmentation strategies: (1) Generating more faces of existing identities. (2) Generating faces of new identities by mixing existing identity label. For strategy 1, we generate 200 images for each person in training set and get totally 100k images. For strategy 2, we first randomly sample 5k new identities by linearly interpolating three existing identity label, and then generate 100 images for each new identity, getting totally 500k images. The generated images are combined with original FaceScrub dataset to train face recognition model. The models used in this experiment are Light CNN29 [20] and Concentrate Loss [10].
At the testing stage, we use the output of penultimate fc layer as face feature. We adopt cosine similarity as metric for Light CNN29 and euclidean distance for Concentrate Loss. We compare the LFW accuracy with and without data augmentation, as shown in Table 2. We can observe that, Light CNN29 gets 1.30% improvement (from 92.23% to 93.53%) with existing ID augmentation and 0.90% improvement (from 92.23% to 93.13%) with new ID augmentation. Consistently, Concentrate Loss gets 1.10% improvement (from 93.12% to 94.22%) with existing ID augmentation and 1.08% improvement (from 93.12% to 94.20%) with new ID augmentation. This demonstrates that our method can be used for data augmentation effectively and bring improvement for face recognition.
5 Conclusion
In this paper, we propose a conditional face synthesis framework that combines a variational auto-encoder with a conditional generative adversarial network, for synthesizing face images with specific identity. To improve image quality, we adopt multi-scale discriminators. Furthermore, we incorporate identity-preserving loss and classification loss to ensure identity invariance of synthesized images, and use feature matching loss to stabilize the GAN training. Experimental results demonstrate that our approach not only produces realistic, discriminative and diverse images but also is available for data augmentation.
References
Arjovsky, M., Bottou, L.: Towards principled methods for training generative adversarial networks. arXiv preprint arXiv:1701.04862 (2017)
Arjovsky, M., Chintala, S., Bottou, L.: Wasserstein generative adversarial networks. In: International Conference on Machine Learning, pp. 214–223 (2017)
Bao, J., Chen, D., Wen, F., Li, H., Hua, G.: CVAE-GAN: fine-grained image generation through asymmetric training. arXiv preprint arXiv:1703.10155 (2017)
Chen, Z., Nie, S., Wu, T., Healey, C.G.: High resolution face completion with multiple controllable attributes via fully end-to-end progressive generative adversarial networks. arXiv preprint arXiv:1801.07632 (2018)
Choi, Y., Choi, M., Kim, M., Ha, J.W., Kim, S., Choo, J.: StarGAN: unified generative adversarial networks for multi-domain image-to-image translation. arXiv preprint arXiv:1711.09020 (2017)
Doersch, C.: Tutorial on variational autoencoders. arXiv preprint arXiv:1606.05908 (2016)
Goodfellow, I., et al.: Generative adversarial nets. In: Advances in Neural Information Processing Systems, pp. 2672–2680 (2014)
Gulrajani, I., Ahmed, F., Arjovsky, M., Dumoulin, V., Courville, A.C.: Improved training of wasserstein gans. In: Advances in Neural Information Processing Systems, pp. 5769–5779 (2017)
Huang, G.B., Ramesh, M., Berg, T., Learned-Miller, E.: Labeled faces in the wild: a database for studying face recognition in unconstrained environments. Technical Report 07–49, University of Massachusetts, Amherst (2007)
Huang, R., Xie, X., Feng, Z., Lai, J.: Face recognition by landmark pooling-based CNN with concentrate loss. In: IEEE International Conference on Image Processing, pp. 1582–1586 (2017)
Huang, R., Zhang, S., Li, T., He, R., et al.: Beyond face rotation: global and local perception GAN for photorealistic and identity preserving frontal view synthesis. arXiv preprint arXiv:1704.04086 (2017)
Johnson, J., Alahi, A., Fei-Fei, L.: Perceptual losses for real-time style transfer and super-resolution. In: Leibe, B., Matas, J., Sebe, N., Welling, M. (eds.) ECCV 2016. LNCS, vol. 9906, pp. 694–711. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-46475-6_43
Kingma, D.P., Ba, J.: Adam: a method for stochastic optimization. arXiv preprint arXiv:1412.6980 (2014)
Krizhevsky, A., Sutskever, I., Hinton, G.E.: ImageNet classification with deep convolutional neural networks. In: Advances in Neural Information Processing Systems, pp. 1097–1105 (2012)
Ledig, C., et al.: Photo-realistic single image super-resolution using a generative adversarial network, 2016. arXiv preprint arXiv:1609.04802 (2017)
Mirza, M., Osindero, S.: Conditional generative adversarial nets. arXiv preprint arXiv:1411.1784 (2014)
Ng, H.W., Winkler, S.: A data-driven approach to cleaning large face datasets. In: 2014 IEEE International Conference on Image Processing (ICIP), pp. 343–347. IEEE (2014)
Salimans, T., Goodfellow, I., Zaremba, W., Cheung, V., Radford, A., Chen, X.: Improved techniques for training GANs. In: Advances in Neural Information Processing Systems, pp. 2234–2242 (2016)
Wang, T.C., Liu, M.Y., Zhu, J.Y., Tao, A., Kautz, J., Catanzaro, B.: High-resolution image synthesis and semantic manipulation with conditional GANs. arXiv preprint arXiv:1711.11585 (2017)
Wu, X., He, R., Sun, Z., Tan, T.: A light CNN for deep face representation with noisy labels. arXiv preprint arXiv:1511.02683 (2015)
Yi, D., Lei, Z., Liao, S., Li, S.Z.: Learning face representation from scratch. arXiv preprint arXiv:1411.7923 (2014)
Zhang, K., Zhang, Z., Li, Z., Qiao, Y.: Joint face detection and alignment using multitask cascaded convolutional networks. IEEE Signal Process. Lett. 23(10), 1499–1503 (2016)
Zhu, J.Y., et al.: Toward multimodal image-to-image translation. In: Advances in Neural Information Processing Systems, pp. 465–476 (2017)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2018 Springer Nature Switzerland AG
About this paper
Cite this paper
Huang, R., Xie, X., Lai, J., Feng, Z. (2018). Conditional Face Synthesis for Data Augmentation. In: Lai, JH., et al. Pattern Recognition and Computer Vision. PRCV 2018. Lecture Notes in Computer Science(), vol 11258. Springer, Cham. https://doi.org/10.1007/978-3-030-03338-5_12
Download citation
DOI: https://doi.org/10.1007/978-3-030-03338-5_12
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03337-8
Online ISBN: 978-3-030-03338-5
eBook Packages: Computer ScienceComputer Science (R0)