Abstract
This paper initiates a study of Fine Grained Secure Computation: i.e. the construction of secure computation primitives against “moderately complex” adversaries. We present definitions and constructions for compact Fully Homomorphic Encryption and Verifiable Computation secure against (non-uniform) \(\mathsf {NC}^1\) adversaries. Our results do not require the existence of one-way functions and hold under a widely believed separation assumption, namely \(\mathsf {NC}^{1}\subsetneq \oplus \mathsf {L}/ {\mathsf {poly}}\). We also present two application scenarios for our model: (i) hardware chips that prove their own correctness, and (ii) protocols against rational adversaries potentially relevant to the Verifier’s Dilemma in smart-contracts transactions such as Ethereum.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Historically, Cryptography has been used to protect information (either in transit or stored) from unauthorized access. One of the most important developments in Cryptography in the last thirty years, has been the ability to protect not only information but also the computations that are performed on data that needs to be secure. Starting with the work on secure multiparty computation [Yao82], and continuing with ZK proofs [GMR89], and more recently Fully Homomorphic Encryption [Gen09], verifiable outsourcing computation [GKR08, GGP10], SNARKs [GGPR13, BCI+13] and obfuscation [GGH+16] we now have cryptographic tools that protect the secrecy and integrity not only of data, but also of the programs which run on that data.
Another crucial development in Modern Cryptography has been the adoption of a more “fine-grained” notion of computational hardness and security. The traditional cryptographic approach modeled computational tasks as “easy” (for the honest parties to perform) and “hard” (infeasible for the adversary). Yet we have also seen a notion of moderately hard problems being used to attain certain security properties. The best example of this approach might be the use of moderately hard inversion problems used in blockchain protocols such as Bitcoin. Although present in many works since the inception of Modern Cryptography, this approach was first formalized in a work of Dwork and Naor [DN92].
In the second part of this work we consider the following model (which can be traced back to the seminal paper by Merkle [Mer78] on public key cryptography). Honest parties will run a protocol which will costFootnote 1 them C while an adversary who wants to compromise the security of the protocol will incur a \(C'=\omega (C)\) cost. Note that while \(C'\) is asymptotically larger than C, it might still be a feasible cost to incur – the only guarantee is that it is substantially larger than the work of the honest parties. For example in Merkle’s original proposal for public-key cryptography the honest parties can exchange a key in time T but the adversary can only learn the key in time \(T^2\). Other examples include primitives introduced by Cachin and Maurer [CM97] and Hastad [Has87] where the cost is the space and parallel time complexity of the parties, respectively.
Recently there has been renewed interest in this model. Degwekar et al. [DVV16] show how to construct certain cryptographic primitives in \(\mathsf {NC}^1\) [resp. \(\mathsf {AC}^0\)] which are secure against all adversaries in \(\mathsf {NC}^1\) [resp. \(\mathsf {AC}^0\)]. In conceptually related work Ball et al. [BRSV17] present computational problems which are “moderately hard” on average, if they are moderately hard in the worst case, a useful property for such problems to be used as cryptographic primitives.
The goal of this paper is to initiate a study of Fine Grained Secure Computation. By doing so we connect these two major developments in Modern Cryptography. The question we ask is if it is possible to construct secure computation primitives that are secure against “moderately complex” adversaries. We answer this question in the affirmative, by presenting definitions and constructions for the task of Fully Homomorphic Encryption and Verifiable Computation in the fine-grained model. In our constructions, our goal is to optimize at the same time (for the extent to which it is possible) in terms of depth, size, round and communication complexity. Our constructions rely on a widely believed complexity separationFootnote 2. We also present two application scenarios for our model: (i) hardware chips that prove their own correctness and (ii) protocols against rational adversaries including potential solutions to the Verifier’s Dilemma in smart-contracts transactions such as Ethereum.
1.1 Our Results
Our starting point is the work in [DVV16] and specifically their public-key encryption scheme secure against \(\mathsf {NC}^1\) circuits. Recall that \(\mathsf {AC}^0[2]\) is the class of Boolean circuits with constant depth, unbounded fan-in, augmented with parity gates. If the number of \(\mathsf {AND}\) (and \(\mathsf {OR}\)) gates of non constant fan-in is constant we say that the circuit belongs to the class \(\mathsf {AC}^0_{\text {Q}}[2]\subset \mathsf {AC}^0[2]\).
Our results can be summarized as follows:
-
We first show that the techniques in [DVV16] can be used to build a somewhat homomorphic encryption (SHE) scheme. We note that because honest parties are limited to \(\mathsf {NC}^1\) computations, the best we can hope is to have a scheme that is homomorphic for computations in \(\mathsf {NC}^1\). However our scheme can only support computations that can be expressed in \(\mathsf {AC}^0_{\text {Q}}[2]\).
-
We then use our SHE scheme, in conjunction with protocols described in [GGP10, CKV10, AIK10], to construct verifiable computation protocols for functions in \(\mathsf {AC}^0_{\text {Q}}[2]\), secure and input/output private against any adversary in \(\mathsf {NC}^1\).
Our somewhat homomorphic encryption also allows us to obtain the following protocols secure against \(\mathsf {NC}^1\) adversaries: (i) constant-round 2PC, secure in the presence of semi-honest static adversaries for functions in \(\mathsf {AC}^0_{\text {Q}}[2]\); (ii) Private Function Evaluation in a two party setting for circuits of constant multiplicative depth without relying on universal circuits. These results stem from well-known folklore transformations and we do not prove them formally.
The class \(\mathsf {AC}^0_{\text {Q}}[2]\) includes many natural and interesting problems such as: fixed precision arithmetic, evaluation of formulas in 3CNF (or kCNF for any constant k), a representative subset of SQL queries, and S-Boxes [BP11] for symmetric key encryption.
Our results (like [DVV16]) hold under the assumption that \(\mathsf {NC}^1 \subsetneq \oplus \mathsf {L}/ {\mathsf {poly}}\), a widely believed worst-case assumption on separation of complexity classes. Notice that this assumption does not imply the existence of one-way functions (or even \(\mathsf {P}\not = \mathsf {NP}\)). Thus, our work shows that it is possible to obtain “advanced” cryptographic schemes, such as somewhat homomorphic encryption and verifiable computation, even if we do not live in MinicryptFootnote 3 Footnote 4.
Comparison with other approaches. One important question is: on what features are our schemes better than “generic” cryptographic schemes that after all are secure against any polynomial time adversary.
One such feature is the type of assumption one must make to prove security. As we said above, our schemes rely on a very mild worst-case complexity assumption, while cryptographic SHE and VC schemes rely on very specific assumptions, which are much stronger than the above.
For the case of Verifiable Computation, we also have information-theoretic protocols which are secure against any (possibly computationally unbounded) adversary. For example the “Muggles” protocol in [GKR08] which can compute any (log-space uniform) \(\mathsf {NC}\) function, and is also reasonably efficient in practice [CMT12]. Or, the more recent work [GR18], which obtains efficient VC for functions in a subset of \(\mathsf {NC}\cap {\mathsf {SC}}\). Compared to these results, one aspect in which our protocol fares better is that our Prover/Verifier can be implemented with a constant-depth circuit (in particular in \(\mathsf {AC}^0[2]\), see Sect. 4) which is not possible for the Prover/Verifier in [GKR08, GR18], which needsFootnote 5 to be in \(\mathsf {TC}^0\). Moreover our protocol is non-interactive (while [GKR08, GR18] requires \(\varOmega (1)\) rounds of interaction) and because our protocols work in the “pre-processing model” we do not require any uniformity or regularity condition on the circuit being outsourced (which are required by [GKR08, CMT12]). Finally, out verification scheme achieves input and output privacy.
Another approach to obtain information-theoretic security for Verifiable Computation is to use the framework of randomized encodings (RE) [IK00a, AIK04] (e.g. [GGH+07] which uses related techniques). In this work we build scheme with additional requirements: compact homomorphic encryptionFootnote 6 and overall efficient verification for verifiable computationFootnote 7. We do not see how to achieve these additional requirements via current RE-based approaches. We further discuss these and other limitations of directly using RE in Appendix D.
1.2 Overview of Our Techniques
Homomorphic Encryption. In [DVV16] the authors already point out that their scheme is linearly homomorphic. We make use of the re-linearization technique from [BV14] to construct a leveled homomorphic encryption.
Our scheme (as the one in [DVV16]) is secure against adversaries in the class of (non-uniform) \(\mathsf {NC}^1\). This implies that we can only evaluate functions in \(\mathsf {NC}^1\) otherwise the evaluator would be able to break the semantic security of the scheme. However we have to ensure that the whole homomorphic evaluation stays in \(\mathsf {NC}^1\). The problem is that homomorphically evaluating a function f might increase the depth of the computation.
In terms of circuit depth, the main overhead will be (as usual) the computation of multiplication gates. As we show in Sect. 3 a single homomorphic multiplication can be performed by a depth two \(\mathsf {AC}^0[2]\) circuit, but this requires depth \(O(\log (n))\) with a circuit of fan-in two. Therefore, a circuit for f with \(\omega (1)\) multiplicative depth would require an evaluation of \(\omega (\log (n))\) depth, which would be out of \(\mathsf {NC}^1\). Therefore our first scheme can only evaluate functions with constant multiplicative depth, as in that case the evaluation stays in \(\mathsf {AC}^0[2]\).
We then present a second scheme that extends the class of computable functions to \(\mathsf {AC}^0_{\text {Q}}[2]\) by allowing for a negligible error in the correctness of the scheme. We use techniques from a work by Razborov [Raz87] on approximating \(\mathsf {AC}^0[2]\) circuits with low-degree polynomials – the correctness of the approximation (appropriately amplified) will be the correctness of our scheme.
Reusable Verifiable Computation. The core of our approach is the construction in [CKV10], to derive Verifiable Computation from Homomorphic Encryption. The details of this approach follow. Recall that we are working in a model with an expensive preprocessing phase (executed by the Client only once and before providing any inputs to the Server) and an inexpensive online phase. The online phase is in turn composed by two algorithms, an algorithm to encode the input for the Server and one to check its response. In the preprocessing phase in [CKV10], the Client selects a random input r, encrypts it as \(c_r=E(r)\) and homomorphically compute \(c_{f(r)}\) an encryption of f(r). During the online phase, the Client, on input x, computes \(c_x=E(x)\) and submits the ciphertexts \(c_x,c_r\) in random order to the Server, who homomorphically computes \(c_{f(r)}=E(f(r))\) and \(c_{f(x)}=E(f(x))\) and returns them to the Client. The Client, given the message \(c_0,c_1\) from the Server, checks that \(c_b=c_{f(r)}\) (for the appropriate bit b) and if so accepts \(y=D(c_{f(x)})\) as \(y=f(x)\). The semantic security of E guarantees that this protocol has soundness error  . This error can be reduce by “scaling” this approach replacing the two ciphertexts \(c_x\) and \(c_r\) with 2t ciphertexts (t distinct encryptions of x and t encryptions of random values \(r_1,\dots ,r_t\) ) sent to the prover after being shuffled through a random permutation. The scheme as described is however one-time secure, since a malicious server can figure out which one is the test ciphertext \(c_{f(r)}\) if it is used again. To make this scheme “many-times secure”, [CKV10] uses the paradigm introduced in [GGP10] of running the one-time scheme “under the hood” of a different homomorphic encryption key each time.
. This error can be reduce by “scaling” this approach replacing the two ciphertexts \(c_x\) and \(c_r\) with 2t ciphertexts (t distinct encryptions of x and t encryptions of random values \(r_1,\dots ,r_t\) ) sent to the prover after being shuffled through a random permutation. The scheme as described is however one-time secure, since a malicious server can figure out which one is the test ciphertext \(c_{f(r)}\) if it is used again. To make this scheme “many-times secure”, [CKV10] uses the paradigm introduced in [GGP10] of running the one-time scheme “under the hood” of a different homomorphic encryption key each time.
When applying these techniques in our fine-grained context the main technical challenge is to guarantee that they would also work within \(\mathsf {NC}^1\). In particular, we needed to ensure that: (i) the constructions can be computed in low-depth; (ii) the reductions in the security proofs can be carried out in low-depth. We rely on results from [MV91] to make sure a random permutation can be sampled by an appropriately low-depth schemeFootnote 8 Moreover, we cannot simply make black-box use of the one-time construction in [CKV10]. In fact, their construction works only for homomorphic encryption schemes with deterministic evaluation, whereas the more expressive of our constructions (Sect. 3.3) is randomizedFootnote 9.
1.3 Application Scenarios
The applications described in this section refer to the problem of Verifying Computation, where a Client outsources an algorithm f and an input x to a Server, who returns a value y and a proof that \(y=f(x)\). The security property is that it should be infeasible to convince the verifier to accept \(y' \ne f(x)\), and the crucial efficiency property is that verifying the proof should cost less than computing f (since avoiding that cost was the reason the Client hired the Server to compute f).
Hardware Chips That Prove Their Own Correctness Verifiable Computation (VC) can be used to verify the execution of hardware chips designed by untrusted manufacturers. One could envision chips that provide (efficient) proofs of their correctness for every input-output computation they perform. These proofs must be efficiently verified in less time and energy than it takes to re-execute the computation itself.
When working in hardware, however, one may not need the full power of cryptographic protection against any malicious attacks since one could bound the computational power of the malicious chip. The bound could be obtained by making (reasonable and evidence-based) assumptions on how much computational power can fit in a given chip area. For example one could safely assume that a malicious chip can perform at most a constant factor more work than the original function because of the basic physics of the size and power constraints. In other words, if C is the cost of the honest Server in a VC protocol, then in this model the adversary is limited to O(C)-cost computations, and therefore a protocol that guarantees that successful cheating strategies require \(\omega (C)\) cost, will suffice. This is exactly the model in our paper. Our results will apply to the case in which we define the cost as the depth (i.e. the parallel time complexity) of the computation implemented in the chip.
Rational Proofs. The problem above is related to the notion of composable Rational Proofs defined in [CG15]. In a Rational Proof (introduced by Azar and Micali [AM12, AM13]), given a function f and an input x, the Server returns the value \(y=f(x)\), and (possibly) some auxiliary information, to the Client. The Client in turn pays the Server for its work with a reward based on the transcript exchanged with the server and some randomness chosen by the client. The crucial property is that this reward is maximized in expectation when the server returns the correct value y. Clearly a rational prover who is only interested in maximizing his reward, will always answer correctly.
The authors of [CG15] show however that the definition of Rational Proofs in [AM12, AM13] does not satisfy a basic compositional property needed for the case in which many computations are outsourced to many servers who compete with each other for rewards (e.g. the case of volunteer computations [ACK+02]). A “rational proof” for the single-proof setting may no longer be rational when a large number of “computation problems” are outsourced. If one can produce T “random guesses” to problems in the time it takes to solve 1 problem correctly, it may be preferable to guess! That’s because even if each individual reward for an incorrect answer is lower than the reward for a correct answer, the total reward of T incorrect answers might be higher (and this is indeed the case for some of the protocols presented in [AM12, AM13]).
The question (only partially answered in [CG15, CG17] for a limited class of computations) is to design protocols where the reward is strictly connected, not just to the correctness of the result, but to the amount of work done by the prover. Consider for example a protocol where the prover collects the reward only if he produces a proof of correctness of the result. Assume that the cost to produce a valid proof for an incorrect result, is higher than just computing the correct result and the correct proof. Then obviously a rational prover will always answer correctly, because the above strategy of fast incorrect answers will not work anymore. While the application is different, the goal is the same as in the previous verifiable hardware scenario.
The Verifier’s Dilemma. In blockchain systems such as Ethereum, transactions can be expressed by arbitrary programs. To add a transaction to a block miners have to verify its validity, which could be too costly if the program is too complex. This creates the so-called Verifier’s Dilemma [LTKS15]: given a costly valid transaction Tr a miner who spends time verifying it is at a disadvantage over a miner who does not verify it and accept it “uncritically” since the latter will produce a valid block faster and claim the reward. On the other hand if the transaction is invalid, accepting it without verifying it first will lead to the rejection of the entire block by the blockchain and a waste of work by the uncritical miner. The solution is to require efficiently verifiable proofs of validity for transactions, an approach already pursued by various startups in the Ethereum ecosystem (e.g. TrueBitFootnote 10). We note that it suffices for these proofs to satisfy the condition above: i.e. we do not need the full power of information-theoretic or cryptographic security but it is enough to guarantee that to produce a proof of correctness for a false transaction is more costly than producing a valid transaction and its correct proof, which is exactly the model we are proposing.
1.4 Future Directions
Our work opens up many interesting future directions.
First of all, it would be nice to extend our results to the case where cost is the actual running time, rather than “parallel running time”/“circuit depth” as in our model. The techniques in [BRSV17] (which presents problems conjectured to have \(\varOmega (n^2)\) complexity on the average), if not even the original work of Merkle [Mer78], might be useful in building a verifiable computation scheme where if computing the function takes time T, then producing a false proof of correctness would have to take \(\varOmega (T^2)\).
For the specifics of our constructions it would be nice to “close the gap” between what we can achieve and the complexity assumption: our schemes can only compute \(\mathsf {AC}^0_{\text {Q}}[2]\) against adversaries in \(\mathsf {NC}^1\), and ideally we would like to be able to compute all of \(\mathsf {NC}^1\) (or at the very least all of \(\mathsf {AC}^0[2]\)).
Finally, to apply these schemes in practice it is important to have tight concrete security reductions and a proof-of-concept implementations.
2 Preliminaries
For a distribution D, we denote by \(x \leftarrow D\) the fact that x is being sampled according to D. We remind the reader that an ensemble \(\mathcal {X} = \{X_{\lambda }\}_{\lambda \in \mathbb {N}}\) is a family of probability distributions over a family of domains \(\mathcal {D}=\{D_{\lambda }\}_{\lambda \in \mathbb {N}}\). We say two ensembles \(\mathcal {D} = \{D_{\lambda }\}_{\lambda \in \mathbb {N}}\) and \(\mathcal {D}' = \{D'_{\lambda }\}_{\lambda \in \mathbb {N}}\) are statistically indistinguishable if
 . Finally, we note that all arithmetic computations (such as sums, inner product, matrix products, etc.) in this work will be over \(\text {GF}(2)\) unless specified otherwise.
. Finally, we note that all arithmetic computations (such as sums, inner product, matrix products, etc.) in this work will be over \(\text {GF}(2)\) unless specified otherwise.
Definition 2.1
(Function Family). A function family is a family of (possibly randomized) functions \(F = \{f_{\lambda }\}_{\lambda \in \mathbb {N}}\), where for each \(\lambda \), \(f_{\lambda }\) has domain \(D^f_{\lambda }\) and co-domain \(R^f_{\lambda }\). A class \(\mathcal {C}\) is a collection of function families.
In most of our constructions \(D^f_{\lambda }=\{0,1\}^{d_\lambda ^f}\) and \(R^f_{\lambda }=\{0,1\}^{r_\lambda ^f}\) for sequences \(\{d_\lambda ^f\}_\lambda \), \(\{d_\lambda ^f\}_\lambda \).
In the rest of the paper we will focus on the class of \(\mathcal {C}=\mathsf {NC}^1\) of functions for which there is a polynomial \(p(\cdot )\) and a constant c such that for each \(\lambda \), the function \(f_\lambda \) can be computed by a Boolean (randomized) fan-in 2, circuit of size \(p(\lambda )\) and depth \(c \log (\lambda )\). In the formal statements of our results we will also use the following classes: \(\mathsf {AC}^0\), the class of functions of polynomial size and constant depth with \(\mathsf {AND}, \mathsf {OR}\) and \(\mathsf {NOT}\) gates with unbounded fan-in; \(\mathsf {AC}^0[2]\), the class of functions of polynomial size and constant depth with \(\mathsf {AND}, \mathsf {OR}, \mathsf {NOT}\) and \(\mathsf {PARITY}\) gates with unbounded fan-in.
Given a function f, we can think of its multiplicative depth as the degree of the lowest-degree polynomial in \(\text {GF}(2)\) that evaluates to f. We denote by \(\mathsf {AC}^0_{\text {CM}}[2]\) the class of circuits in \(\mathsf {AC}^0[2]\) with constant multiplicative depth. We say that a circuit has quasi-constant multiplicative depth if it has a constant number of gates with non-constant fan-in (an example is a circuit composed by a single \(\mathsf {AND}\) of fan-in n). We denote the class of such circuits by \(\mathsf {AC}^0_{\text {Q}}[2]\). See Appendix A for a formal treatment.
Limited Adversaries. We define adversaries also as families of randomized algorithms \(\{A_\lambda \}_\lambda \), one for each security parameter (note that this is a non-uniform notion of security). We denote the class of adversaries we consider as \(\mathcal {A}\), and in the rest of the paper we will also restrict \(\mathcal {A}\) to \(\mathsf {NC}^1\).
Infinitely-Often Security. We now move to define security against all adversaries \(\{A_\lambda \}_\lambda \) that belong to a class \(\mathcal {A}\). Our results achieve an “infinitely often” notion of security, which states that for all adversaries outside of our permitted class \(\mathcal {A}\) our security property holds infinitely often (i.e. for an infinite sequence of security parameters rather than for every sufficiently large security parameter). This limitation seems inherent to the techniques in this paper and in [DVV16]. We informally denote with \(\mathcal {X} \sim _{\varLambda } \mathcal {Y}\) the fact that two ensembles \(\mathcal {X}\) and \(\mathcal {Y}\) are indistinguishable by \(\mathsf {NC}^1\) adversaries for an infinite sequence of parameters \(\varLambda \). See also Appendix A.
3 Fine-Grained SHE
We start by recalling the public key encryption from [DVV16] which is secure against adversaries in \(\mathsf {NC}^1\).
The scheme is described in Fig. 1. Its security relies on the following result, implicit in [IK00a]Footnote 11. We will also use this lemma when proving the security of our construction in Sect. 3.
Lemma 3.1
([IK00a]). If \(\mathsf {NC}^1 \subsetneq \oplus \mathsf {L}/ {\mathsf {poly}}\) then there exist distribution \(\mathcal {D}^{\text {kg}}_{\lambda }\) over \(\{0, 1\}^{\lambda \times \lambda }\), distribution \(\mathcal {D}^{f}_{\lambda }\) over matrices in \(\{0, 1\}^{\lambda \times \lambda }\) of full rank, and infinite set \(\varLambda \subseteq \mathbb {N}\) such that
where \(\mathbf {M}^{\mathcal {\text {f}}}\leftarrow \mathcal {D}^{f}_{\lambda }\) and \(\mathbf {M}^{\text {kg}}\leftarrow \mathcal {D}^{\text {kg}}_{\lambda }\).
The following result is central to the correctness of the scheme \(\mathsf {PKE}\) in Fig. 1 and is implicit in [DVV16].
Lemma 3.2
([DVV16]). There exists sampling algorithm \(\mathsf {KSample}\) such that \((\mathbf {M}, \mathbf {k}) \leftarrow \mathsf {KSample}(1^{\lambda })\), \(\mathbf {M}\) is a matrix distributed according to \(\mathcal {D}^{\text {kg}}_{\lambda }\) (as in Lemma 3.1), \(\mathbf {k}\) is a vector in the kernel of \(\mathbf {M}\) and has the form
\(\mathbf {k}= (r_1, \, r_2, \, \dots , \, r_{\lambda -1}, \, 1) \in \{0, 1\}^{\lambda }\) where \(r_i\)-s are uniformly distributed bits.
PKE construction [DVV16]
Theorem 3.1
([DVV16]). Assume \(\mathsf {NC}^1 \subsetneq \oplus \mathsf {L}/ {\mathsf {poly}}\). Then, the scheme \(\mathsf {PKE}= (\mathsf {PKE.Keygen}, \mathsf {PKE.Enc}, \mathsf {PKE.Dec})\) defined in Fig. 1 is a Public Key Encryption scheme secure against \(\mathsf {NC}^1\) adversaries. All algorithms in the scheme are computable in \(\mathsf {AC}^0[2]\).
3.1 Leveled Homomorphic Encryption for \(\mathsf {AC}^0_{\text {CM}}[2]\) Functions Secure Against \(\mathsf {NC}^1\)
We denote by \(\varvec{x}[i]\) the i-th bit of a vector of bits \(\varvec{x}\) . Below, the scheme \(\mathsf {PKE}= (\mathsf {PKE.Keygen},\mathsf {PKE.Enc}, \mathsf {PKE.Dec})\) is the one defined in Fig. 1. Our SHE scheme is defined by the following four algorithms:
-
\(\mathsf {HE.Keygen}_{\mathsf {sk}}(1^{\lambda }, L):\) For key generation, sample \(L+1\) key pairs \((\mathbf {M}_0, \mathbf {k}_0),\dots ,(\mathbf {M}_L, \mathbf {k}_L) \leftarrow \mathsf {PKE.Keygen}(1^{\lambda })\), and compute, for all \(\ell \in \{0, \dots , L-1\}\), \(i,j \in [\lambda ]\), the value
$$ \varvec{a}_{\ell ,i,j} \leftarrow \mathsf {PKE.Enc}_{\mathbf {M}_{\ell +1}}(\mathbf {k}_{\ell }[i]\cdot \mathbf {k}_{\ell }[j]) \in \{0, 1\}^{\lambda }$$We define
 to be the set of all these values. t then outputs the secret key \(\mathsf {sk}= \mathbf {k}_L\), and the public key \(\mathsf {pk}= (\mathbf {M}_0, \mathbf {A})\). In the following we call \(\mathsf {evk}= \mathbf {A}\) the evaluation key. We point out a property that will be useful later: by the definition above, for all \(\ell \in \{0, \dots , L-1 \}\) we have $$\begin{aligned} \langle \mathbf {k}_{\ell +1} \, , \varvec{a}_{\ell +1,i,j} \rangle = \mathbf {k}_{\ell }[i] \cdot \mathbf {k}_{\ell }[j]\,. \end{aligned}$$(1)
to be the set of all these values. t then outputs the secret key \(\mathsf {sk}= \mathbf {k}_L\), and the public key \(\mathsf {pk}= (\mathbf {M}_0, \mathbf {A})\). In the following we call \(\mathsf {evk}= \mathbf {A}\) the evaluation key. We point out a property that will be useful later: by the definition above, for all \(\ell \in \{0, \dots , L-1 \}\) we have $$\begin{aligned} \langle \mathbf {k}_{\ell +1} \, , \varvec{a}_{\ell +1,i,j} \rangle = \mathbf {k}_{\ell }[i] \cdot \mathbf {k}_{\ell }[j]\,. \end{aligned}$$(1) -
\(\mathsf {HE.Enc}_{\mathsf {pk}}(\mu )):\) Recall that \(\mathsf {pk}= \mathbf {M}_0\). To encrypt a message \(\mu \) we compute \(\varvec{v} \leftarrow \mathsf {PKE.Enc}_{\mathbf {M}_0}(\mu )\). The output ciphertext contains \(\varvec{v}\) in addition to a “level tag”, an index in \(\{0, \dots , L \}\) denoting the “multiplicative depth” of the generated ciphertext. The encryption algorithm outputs
 .
. -
\(\mathsf {HE.Dec}_{\mathbf {k}_L}(c):\) To decrypt a ciphertextFootnote 12 \(c = (\varvec{v},L)\) compute \(\mathsf {PKE.Dec}_{\mathbf {k}_L}(\varvec{v})\), i.e.
$$ \langle \mathbf {k}_L \, , \varvec{v} \rangle $$ -
\(\mathsf {HE.Eval}_{\mathsf {evk}}(f, c_1,\dots ,c_n):\) where \(f : \{0, 1\}^n \rightarrow \{0, 1\}\): We require that f is represented as an arithmetic circuit in \(\text {GF}(2)\) with addition gates of unbounded fan-in and multiplication gates of fan-in 2. We also require the circuit to be layered, i.e. the set of gates can be partitioned in subsets (layers) such that wires are always between adjacent layers. Each layer should be composed homogeneously either of addition or multiplication gates. Finally, we require that the number of multiplications layers (i.e. the multiplicative depth) of f is L. We homomorphically evaluate f gate by gate. We will show how to perform multiplication (resp. addition) of two (resp. many) ciphertexts. Carrying out this procedure recursively we can homomorphically compute any circuit f of multiplicative depth L.
Ciphertext Structure During Evaluation. During the homomorphic evaluation a ciphertext will be of the form \(c = (\varvec{v}, \ell )\) where \(\ell \) is the “level tag” mentioned above. At any point of the evaluation we will have that \(\ell \) is between 0 (for fresh ciphertexts at the input layer) and L (at the output layer). We define homomorphic evaluation only among ciphertexts at the same level. Since our circuit is layered we will not have to worry about homomorphic evaluation occurring among ciphertexts at different levels. Consistently with the fact a level tag represents the multiplicative depth of a ciphertext, addition gates will keep the level of ciphertexts unchanged, whereas multiplication gates will increase it by one. Finally, we will keep the invariant that the output of each gate evaluation \(c = (\varvec{v}, \ell )\) is such that
where \(\mu \) is the correct plaintext output of the gate. We prove our construction satisfies this invariant in Appendix B.
Homomorphic Evaluation of Gates:
-
Addition gates. Homomorphic evaluation of an addition gates on inputs \(c_1,\dots ,c_n\) where \(c_i = (\varvec{v}_i, \ell )\) is performed by outputting

-
Multiplication gates. We show how to multiply ciphertexts \(c, c'\) where \(c = (\varvec{v}, \ell )\) and \(c' = (\varvec{v}', \ell )\) to obtain an output ciphertext \(c_{\text {mult}} = (\varvec{v}_{\text {mult}}, \ell +1)\). The homomorphic multiplication algorithm will set

where \(h_{i,j} = \varvec{v}[i] \cdot \varvec{v}'[j]\) for \(i,j \in [\lambda ]\). The final output ciphertext will be

The following theorem states the security of our scheme under our complexity assumption.
Theorem 3.2
(Security). The scheme \(\mathsf {HE}\) is \(\text {CPA}\) secure against \(\mathsf {NC}^1\) adversaries (Definition A.5) under the assumption \(\mathsf {NC}^1 \subsetneq \oplus \mathsf {L}/ {\mathsf {poly}}\).
3.2 Efficiency and Homomorphic Properties of Our Scheme
Our scheme is secure against adversaries in the class \(\mathsf {NC}^1\). This implies that we can run \(\mathsf {HE.Eval}\) only on functions f that are in \(\mathsf {NC}^1\), otherwise the evaluator would be able to break the semantic security of the scheme. However we have to ensure that the whole homomorphic evaluation stays in \(\mathsf {NC}^1\). The problem is that homomorphically evaluating f has an overhead with respect to the “plain” evaluation of f. Therefore, we need to determine for which functions f, we can guarantee that \(\mathsf {HE.Eval}(F, \dots )\) will stay in \(\mathsf {NC}^1\). The class of such functions turns out to be the class of functions implementable in constant multiplicative depth, i.e. \(\mathsf {AC}^0_{\text {CM}}[2]\)Footnote 13.
These observations, plus the fact that the invariant in Eq. 2 is preserved throughout homomorphic evaluation, imply the following result.
Theorem 3.3
The scheme \(\mathsf {HE}\) is leveled \(\mathsf {AC}^0_{\text {CM}}[2]\)-homomorphic. Key generation, encryption, decryption and evaluation are all computable in \(\mathsf {AC}^0_{\text {CM}}[2]\).
3.3 Beyond Constant Multiplicative Depth
In the previous section we saw how our scheme is homomorphic for a class of constant-depth, unbounded fan-in arithmetic circuits in \(\text {GF}(2)\) with constant multiplicative depth. We now show how to overcome this limitation by first extending techniques from [Raz87] to approximate \(\mathsf {AC}^0[2]\) circuits with low-degree polynomials and then designing a construction that internally uses our scheme \(\mathsf {HE}\) from Sect. 3.1.
Approximating \(\varvec{\mathsf {AC}^0_{\text {Q}}[2]}\) in \(\varvec{\mathsf {AC}^0_{\text {CM}}[2]}\) . Our approach to homomorphically evaluate a function \(f \in \mathsf {AC}^0_{\text {Q}}[2]\) is as follows. Instead of evaluating f we evaluate \(f^*\), an approximate version of f that is computable in \(\mathsf {AC}^0_{\text {CM}}[2]\). The function \(f^*\) is randomized and we will denote by \(n'\) the number of random bits \(f^*\) takes in input (in addition to the n bits of the input x). If \(\varvec{\hat{x}} = {\mathsf {Enc}}(x)\) and \(\varvec{\hat{r}} = {\mathsf {Enc}}(r)\) where r is uniformly random in \(\{0, 1\}^{n'}\), then decrypting \(\mathsf {HE.Eval}(f^*, \varvec{\hat{x}}, \varvec{\hat{r}})\)Footnote 14 yields f(x) with constant error probability. One way to reduce error could be to let evaluation compute \(f^*\) s times with s random inputs. However, this requires particular care to avoid using majority gates in the decryption algorithm. With this goal in mind we extend the output of the approximating function \(f^*\). When performing evaluation we will then perform s evaluations of \(f'\), the “extension” of \(f^*\) This additional information will be returned (encrypted) from the evaluation algorithm and will allow correct decryption with overwhelming probability and in low-depth (and without majority gates).
In the next constructions we will make use of the functions \(\mathsf {GenApproxFun}\), \({\mathsf {GenDecodeAux}}\) and \({\mathsf {DecodeApprox}}\), here only informally definedFootnote 15. The function \(\mathsf {GenApproxFun}(f)\) returns the (extended) approximating function \(f'\); the function \({\mathsf {GenDecodeAux}}(f)\) returns a constant-size string \(\mathbf {aux}_f\) used to decode (multiple) output of \(f'(x)\); the function \({\mathsf {DecodeApprox}}(\mathbf {aux}_f, \varvec{y}^{\text {out}}_1, \dots , \varvec{y}^{\text {out}}_s )\) returns f(x) w.h.p. if each \(\varvec{y}^{\text {out}}_s\) is an output of \(f'(x;r)\) for random r.
Homomorphic Evaluations of \(\varvec{\mathsf {AC}^0_{\text {Q}}[2]}\) Circuits. Below is our construction for a homomorphic scheme that can evaluate all circuits in \(\mathsf {AC}^0_{\text {Q}}[2]\) in \(\mathsf {AC}^0[2]\). This time, in order to evaluate circuit C, we perform several homomorphic evaluations of the randomized circuit \(C'\) (as in Lemma B.2). To obtain the plaintext output of C we can decrypt all the ciphertext outputs and use \({\mathsf {DecodeApprox}}\). Notice that this scheme is still compact. As we use a randomized approach to evaluate f, the scheme \(\mathsf {HE'}\) will be implicitly parametrized by a soundness parameter s. Intuitively, the probability of a function f being evaluated incorrectly will be upper bounded by \(2^{-s}\).
For our new scheme we will use the following auxiliary functions:
Definition 3.1
(Auxiliary Functions for \(\mathsf {HE'}\)). Let \(f: \{0, 1\}^n \rightarrow \{0, 1\}\) be represented as an arithmetic circuit as in \(\mathsf {HE}\) and \(\mathsf {pk}\) a public key for the scheme \(\mathsf {HE}\) that includes the evaluation key. Let s be a soundness parameter. We denote by \(f'\) be as above; let \(n' = O(n)\) be the number of additional bits \(f'\) will take as random input.
-
\(\mathsf {SampleAuxRandomness}_s(\mathsf {pk}, f'):\)
-
1.
Sample \(s\cdot n'\) random bits \(r^{(1)}_1,\dots ,r^{(1)}_{n'}, \dots , r^{(s)}_1,\dots ,r^{(s)}_{n'}\);
-
2.
Compute
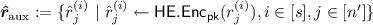 ;
; -
3.
Output \(\varvec{\hat{r}}_{\text {aux}}\).
-
1.
-
\(\mathsf {EvalApprox}_s(\mathsf {pk}, f', c_1,\dots ,c_{n}, \varvec{\hat{r}}_{\text {aux}}):\)
-
1.
Let \(\varvec{\hat{r}}_{\text {aux}}= \{ \hat{r}^{(i)}_j \ | \ i \in [s], j \in [n'] \} \).
-
2.
For \(i \in [s]\), compute \(\varvec{c}^{\text {out}}_i \leftarrow \mathsf {HE.Eval}_{\mathsf {evk}}(f', c_1, \dots c_{n}, \hat{r}^{(i)}_1, \dots , \hat{r}^{(i)}_{n'})\);
-
3.
Output \(\varvec{c} = (\varvec{c}^{\text {out}}_1, \dots , \varvec{c}^{\text {out}}_{s})\)Footnote 16.
-
1.
The new scheme \(\mathsf {HE'}\) with soundness parameter s follows. Notice that the evaluation function outputs an auxiliary string \(\mathbf {aux}_f\) together with the proper ciphertext \(\varvec{c}\). This is necessary to have a correct decoding in decryption phase.

The following theorem summarizes the properties of this construction.
Theorem 3.4
The scheme \(\mathsf {HE'}\) above with soundness parameter \(s = \varOmega (\lambda )\) is leveled \(\mathsf {AC}^0_{\text {Q}}[2]\)-homomorphic. Key generation, encryption and evaluation can be computed in \(\mathsf {AC}^0_{\text {CM}}[2]\). Decryption is computable in \(\mathsf {AC}^0_{\text {Q}}[2]\).
4 Fine-Grained Verifiable Computation
In this section we describe our private verifiable computation scheme. Our constructions are based on the techniques in [CKV10] to obtain (reusable) verifiable computation from fully homomorphic encryption; see Sect. 1.2 for a high-level description.
4.1 A One-time Verification Scheme
In Figure 2 we describe an adaptation of the one-time secure delegation scheme from [CKV10]. We make non-black box use of our homomorphic encryption scheme \(\mathsf {HE'}\) (Sect. 3.3) with soundness parameter \(s= \lambda \). Notice that. during the preprocessing phase, we fix the “auxiliary randomness” for \(\mathsf {EvalApprox}\) (and thus for \(\mathsf {HE'.Eval}\)) once and for all. We will use that same randomness for all the input instances. This choice does not affect the security of the construction. We remind the reader that we will simplify notation by considering the evaluation key of our somewhat homomorphic encryption scheme as part of its public key.
If x is a vector of bits \(x_1, \dots , x_n\), below we will denote with \(\mathsf {HE'.Enc}(x)\) the concatenation of the bit by bit ciphertexts \(\mathsf {HE'.Enc}(x_1), \dots , \mathsf {HE'.Enc}(x_n)\). We denote by \(\mathsf {HE'.Enc}(\bar{0})\) the concatenation of n encryptions of 0, \(\mathsf {HE'.Enc}(0)\).
The scheme \(\mathcal{VC}\) in Figure 2 has overwhelming completeness and is one-time secure when t is chosen \(\omega (\log (\lambda ))\). We prove these results in Appendix C.
Remark 4.1
(Efficiency of \(\mathcal{VC}\)). In the following we consider the verifiable computation of a function \(f: \{0, 1\}^n \rightarrow \{0, 1\}^m\) computable by an \(\mathsf {AC}^0_{\text {Q}}[2]\) circuit of size S.
-
\(\mathsf {VC.KeyGen}\) is computable by an \(\mathsf {AC}^0[2]\) circuit of size \(O({\mathsf {poly}}(\lambda )S)\);
-
\(\mathsf {VC.ProbGen}\) is computable by an \(\mathsf {AC}^0[2]\) circuit of size \(O({\mathsf {poly}}(\lambda )(m+n))\);
-
\(\mathsf {VC.Compute}\) is computable by an \(\mathsf {AC}^0[2]\) circuit of size \(O({\mathsf {poly}}(\lambda )S)\);
-
\(\mathsf {VC.Verify}\) is computable by a \(\mathsf {AC}^0[2]\) circuit of size \(O({\mathsf {poly}}(\lambda )(m+n))\).
The (constant) depth of \(\mathsf {VC.ProbGen}\) and \(\mathsf {VC.Verify}\) is independent of the depth of fFootnote 17.
4.2 A Reusable Verification Scheme
We obtain our reusable verification scheme \(\overline{\mathcal{VC}}\) applying the transformation in [CKV10] from one-time sound verification schemes through fully homomorphic encryption. The core idea behind this transformation is to encapsulate all the operations of a one-time verifiable computation scheme (such as \(\mathcal{VC}\) in Fig. 2) through homomorphic encryption. We instantiate this transformation with the simplest of our two somewhat homomorphic encryption schemes, \(\mathsf {HE}\) (described in Sect. 3.1). The full construction of \(\overline{\mathcal{VC}}\) is in Appendix C (Fig. 3).
Remark 4.2
(Efficiency of \(\overline{\mathcal{VC}}\)). The efficiency of \(\overline{\mathcal{VC}}\) is analogous to that of \(\mathcal{VC}\) with the exception of a circuit size overhead of a factor \(O(\lambda )\) on the problem generation and verification algorithms and of \(O(\lambda ^2)\) for the computation algorithm. The (constant) depth of \(\mathsf {\overline{VC}.ProbGen}\) and \(\mathsf {\overline{VC}.Verify}\) is independent of the depth of f.
Theorem 4.1
(Completeness of \(\overline{\mathcal{VC}}\)). The verifiable computation scheme \(\overline{\mathcal{VC}}\) has overwhelming completeness (Definition A.10) for the class \(\mathsf {AC}^0_{\text {Q}}[2]\).
Theorem 4.2
(Many-Times Soundness of \(\overline{\mathcal{VC}}\)). Under the assumption that \(\mathsf {NC}^1 \subsetneq \oplus \mathsf {L}/ {\mathsf {poly}}\) the scheme \(\overline{\mathcal{VC}}\) is many-times secure against \(\mathsf {NC}^1\) adversaries whenever t is chosen to be \(\omega (\log (\lambda ))\) in the underlying scheme \(\mathcal{VC}\).
Notes
- 1.
We intentionally refer to it as “cost” to keep the notion generic. For concreteness one can think of C as the running time required to run the protocol.
- 2.
A separation implied by \(\mathsf {L}\ne \mathsf {NC}^1\). See Sect. 1.1 for more details.
- 3.
This is a reference to Impagliazzo’s “five possible worlds” [Imp95].
- 4.
Naturally the security guarantees of these schemes are more limited compared to their standard definitions.
- 5.
- 6.
Where the ciphertexts do not grow in size with each homomorphic operation.
- 7.
Where not only the circuit depth is constant but also the size of the circuit is quasilinear – the size of the verification circuit should be \(O({\mathsf {poly}}(\lambda )(n+m))\) where n and m are the size of the input and output respectively.
- 8.
More precisely, that a permutation statistically indistinguishable from a random one can be sampled in \(\mathsf {AC}^0\).
- 9.
See also Remark C.1.
- 10.
TrueBit: https://truebit.io/.
- 11.
Stated as Lemma 4.3 in [DVV16].
- 12.
We are only requiring to decrypt ciphertexts that are output by \(\mathsf {HE.Eval}(\cdots )\).
- 13.
In terms of circuit depth, the main overhead when evaluating f homomorphically is given by the multiplication gates (addition, on the other hand, is “for free” — see definition of \(\mathsf {HE.Eval}\) above). A single homomorphic multiplication can be performed by a depth two \(\mathsf {AC}^0[2]\) circuit, but this requires depth \(\varOmega (\log (n))\) with a circuit of fan-in two. Therefore, a circuit for f with \(\omega (1)\) multiplicative depth would require an evaluation of \(\omega (\log (n))\) depth, which would be out of \(\mathsf {NC}^1\). On the other hand, observe that for any function f in \(\mathsf {AC}^0[2]\) with constant multiplicative depth, the evaluation stays in \(\mathsf {AC}^0[2]\). This because there is a constant number (depth) of homomorphic multiplications each requiring an \(\mathsf {AC}^0[2]\) computation.
- 14.
In the evaluation algorithm we ignore the distinction between deterministic and random input.
- 15.
The reader can find additional details in Appendix B.
- 16.
Recall that the output of the expanded approximating function \(f'\) is a bit string and thus each \(\varvec{c}^{\text {out}}_i\) encrypts a bit string.
- 17.
Further details on the complexity of \(\mathcal{VC}\) follow. All the algorithms are in \(\mathsf {AC}^0_{\text {CM}}[2]\), except for the online stage. In fact, \(\mathsf {VC.Verify}\) and \(\mathsf {VC.ProbGen}\) are in \(\mathsf {AC}^0[2]\). Moreover, they are not in \(\mathsf {AC}^0_{\text {Q}}[2]\) as they perform in parallel a non-constant (polylogarithmic) number of decryptions and permutations respectively, and these involve non-constant fan-in gates. Notice that even though the online stage is not in \(\mathsf {AC}^0_{\text {Q}}[2]\) we still have a gain at verification time (although not in an asymptotic sense). This because of the specific structure of these circuits. Consider for example what happens when implementing \(\mathsf {VC.Verify}\) or \(\mathsf {VC.ProbGen}\) with a fan-in two circuit. Their depth will be \(c (\log (n)+\log (\lambda ))\) for a constant c. Contrast this with a circuit f in \(\mathsf {AC}^0_{\text {Q}}[2]\) of constant depth D that we may want to verify. With fan-in two, the depth of f will become \(c'D\log (n)\) (for a constant \(c'\)), which may be significantly larger.
- 18.
We refer the reader to [Gol01].
- 19.
- 20.
This allows our \(\mathsf {NC}^0\) circuit to “know” which gates to copy and which ones to transform based on their position only.
- 21.
I.e. the size of the verification circuit should be \(O({\mathsf {poly}}(\lambda )(n+m))\) where n and m are the size of the input and output respectively.
- 22.
These observations would not hold for the computational setting, which is out of the scope of this paper.
References
Anderson, D.P., Cobb, J., Korpela, E., Lebofsky, M., Werthimer, D.: SETI@home: an experiment in public-resource computing. Commun. ACM 45(11), 56–61 (2002)
Applebaum, B., Ishai, Y., Kushilevitz, E.: Cryptography in \(NC^{0}\). In: Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, pp. 166–175 (2004)
Applebaum, B., Ishai, Y., Kushilevitz, E.: From secrecy to soundness: efficient verification via secure computation. In: Abramsky, S., Gavoille, C., Kirchner, C., Meyer auf der Heide, F., Spirakis, P.G. (eds.) ICALP 2010. LNCS, vol. 6198, pp. 152–163. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14165-2_14
Azar, P.D., Micali, S.: Rational proofs. In: Proceedings of the Forty-Fourth Annual ACM Symposium on Theory of Computing, pp. 1017–1028. ACM (2012)
Azar, P.D., Micali, S.: Super-efficient rational proofs. In: Proceedings of the Fourteenth ACM Conference on Electronic Commerce, pp. 29–30. ACM (2013)
Bitansky, N., Chiesa, A., Ishai, Y., Paneth, O., Ostrovsky, R.: Succinct non-interactive arguments via linear interactive proofs. In: Sahai, A. (ed.) TCC 2013. LNCS, vol. 7785, pp. 315–333. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-36594-2_18
Boyar, J., Peralta, R.C.: A depth-16 circuit for the AES S-box. IACR Cryptology ePrint Archive (2011)
Ball, M., Rosen, A., Sabin, M., Vasudevan, P.N.: Average-case fine-grained hardness. In: Electronic Colloquium on Computational Complexity (ECCC), vol. 24, p. 39 (2017)
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) lwe. SIAM J. Comput. 43(2), 831–871 (2014)
Campanelli, M., Gennaro, R.: Sequentially composable rational proofs. In: Khouzani, M.H.R., Panaousis, E., Theodorakopoulos, G. (eds.) GameSec 2015. LNCS, vol. 9406, pp. 270–288. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-25594-1_15
Campanelli, M., Gennaro, R.: Efficient rational proofs for space bounded computations. In: Rass, S., An, B., Kiekintveld, C., Fang, F., Schauer, S. (eds.) International Conference on Decision and Game Theory for Security, vol. 10575, pp. 53–73. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-68711-7_4
Chung, K.-M., Kalai, Y., Vadhan, S.: Improved delegation of computation using fully homomorphic encryption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 483–501. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_26
Cachin, C., Maurer, U.: Unconditional security against memory-bounded adversaries. In: Kaliski, B.S. (ed.) CRYPTO 1997. LNCS, vol. 1294, pp. 292–306. Springer, Heidelberg (1997). https://doi.org/10.1007/BFb0052243
Cormode, G., Mitzenmacher, M., Thaler, J.: Practical verified computation with streaming interactive proofs. In: Proceedings of the 3rd Innovations in Theoretical Computer Science Conference, pp. 90–112. ACM (2012)
Dwork, C., Naor, M.: Pricing via processing or combatting junk mail. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 139–147. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-48071-4_10
Degwekar, A., Vaikuntanathan, V., Vasudevan, P.N.: Fine-grained cryptography. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9816, pp. 533–562. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-53015-3_19
Gentry, C.: A fully homomorphic encryption scheme. Stanford University (2009)
Goldwasser, S., Gutfreund, D., Healy, A., Kaufman, T., Rothblum, G.N.: Verifying and decoding in constant depth. In: Proceedings of the Thirty-Ninth Annual ACM Symposium on Theory of Computing, pp. 440–449. ACM (2007)
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. SIAM J. Comput. 45(3), 882–929 (2016)
Gennaro, R., Gentry, C., Parno, B.: Non-interactive verifiable computing: outsourcing computation to untrusted workers. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 465–482. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_25
Gennaro, R., Gentry, C., Parno, B., Raykova, M.: Quadratic span programs and succinct NIZKs without PCPs. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 626–645. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38348-9_37
Goldwasser, S., Kalai, Y.T., Rothblum, G.N.: Delegating computation: interactive proofs for muggles. In: Proceedings of the Fortieth Annual ACM Symposium on Theory of Computing, pp. 113–122. ACM (2008)
Goldwasser, S., Micali, S., Rackoff, C.: The knowledge complexity of interactive proof systems. SIAM J. Comput. 18(1), 186–208 (1989)
Goldreich, O.: Foundations of Cryptography: Basic Tools, vol. 1. Cambridge University Press, New York (2001)
Goldreich, O.: Foundations of Cryptography: Basic Applications, vol. 2. Cambridge University Press, New York (2009)
Goldreich, O., Rothblum, G.N.: Simple doubly-efficient interactive proof systems for locally-characterizable sets. In: LIPIcs-Leibniz International Proceedings in Informatics, vol. 94. Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik (2018)
Hagerup, T.: Fast parallel generation of random permutations. In: Albert, J.L., Monien, B., Artalejo, M.R. (eds.) ICALP 1991. LNCS, vol. 510, pp. 405–416. Springer, Heidelberg (1991). https://doi.org/10.1007/3-540-54233-7_151
Hastad, J.: One-way permutations in NC0. Inf. Process. Lett. 26(3), 153–155 (1987)
Ishai, Y., Kushilevitz, E.: Randomizing polynomials: a new representation with applications to round-efficient secure computation. In: Proceedings of the 41st Annual Symposium on Foundations of Computer Science, pp. 294–304. IEEE (2000)
Ishai, Y., Kushilevitz, E.: Perfect constant-round secure computation via perfect randomizing polynomials. In: Widmayer, P., Eidenbenz, S., Triguero, F., Morales, R., Conejo, R., Hennessy, M. (eds.) ICALP 2002. LNCS, vol. 2380, pp. 244–256. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45465-9_22
Impagliazzo, R.: A personal view of average-case complexity. In: Proceedings of Tenth Annual IEEE Structure in Complexity Theory Conference, pp. 134–147. IEEE (1995)
Luu, L., Teutsch, J., Kulkarni, R., Saxena, P.: Demystifying incentives in the consensus computer. In: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, pp. 706–719. ACM (2015)
Merkle, R.C.: Secure communications over insecure channels. Commun. ACM 21(4), 294–299 (1978)
Matias, Y., Vishkin, U.: Converting high probability into nearly-constant time - with applications to parallel hashing. In: Proceedings of the Twenty-third Annual ACM Symposium on Theory of Computing, STOC 1991, pp. 307–316. ACM, New York (1991)
Razborov, A.A.: Lower bounds on the size of bounded depth circuits over a complete basis with logical addition. Math. Notes Acad. Sci. USSR 41(4), 333–338 (1987)
Sander, T., Young, A., Yung, M.: Non-interactive cryptocomputing for NC1. In: Proceedings of the 40th Annual Symposium on Foundations of Computer Science, p. 554. IEEE Computer Society (1999)
Yao, A.C.: Protocols for secure computations. In: 23rd Annual Symposium on Foundations of Computer Science, SFCS 2008, pp. 160–164. IEEE (1982)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Additional Preliminaries
1.1 A.1 Infinitely-Often Computational Indistinguishability
Definition A.1
(Infinitely-Often Computational Indistinguishability). Let \(\mathcal {X} = \{X_{\lambda }\}_{\lambda \in \mathbb {N}}\) Let \(\mathcal {Y} = \{Y_{\lambda }\}_{\lambda \in \mathbb {N}}\) be ensembles over the same domain family, \(\mathcal {A}\) a class of adversaries, and \(\varLambda \) an infinite subset of \(\mathbb {N}\). We say that \(\mathcal {X}\) and \(\mathcal {Y}\) are infinitely often computational indistinguishable with respect to set \(\varLambda \) and the class \(\mathcal {A}\), denoted by \(\mathcal {X} \sim _{\varLambda ,\mathcal {A}} \mathcal {Y}\) if there exists a negligible function \(\nu \) such that for any \(\lambda \in \varLambda \) and for any adversary \(A=\{A_\lambda \}_\lambda \in \mathcal {A}\)
When \(\mathcal {A} = \mathsf {NC}^1\) we will keep it implicit and use the notation \(\mathcal {X} \sim _{\varLambda } \mathcal {Y}\) and say that \(\mathcal {X} \text { and } \mathcal {Y}\) are \(\varLambda \)-computationally indistinguishable.
In our proofs we will use the following facts on infinitely-often computationally indistinguishable ensembles. We skip their proof as, except for a few technicalities, it is analogous to the corresponding properties for standard computational indistinguishabilityFootnote 18.
Lemma A.1
(Facts on \(\varLambda \)-Computational Indistinguishability).
-
Transitivity: Let \(m = {\mathsf {poly}}(\lambda )\) and \(\mathcal {X}^{(j)}\) with \(j \in \{0,\dots ,m \} \) be ensembles. If for all \(j \in [m]\) \(\mathcal {X}^{(j-1)} \sim _{\varLambda }\mathcal {X}^{(j)}\), then \(\mathcal {X}^{(0)} \sim _{\varLambda }\mathcal {X}^{(m)}\).
-
Weaker than statistical indistinguishability: Let \(\mathcal {X}, \mathcal {Y}\) be statistically indistinguishable ensembles. Then \(\mathcal {X} \sim _{\varLambda }\mathcal {Y}\) for any infinite \(\varLambda \subseteq \mathbb {N}\).
-
Closure under \(\mathsf {NC}^1\): Let \(\mathcal {X}, \mathcal {Y}\) be ensembles and \(\{f_{\lambda }\}_{\lambda \in \mathbb {N}} \in \mathsf {NC}^1\). If \(\mathcal {X} \sim _{\varLambda }\mathcal {Y}\) for some \(\varLambda \) then \(f_{\lambda }(\mathcal {X}) \sim _{\varLambda }f_{\lambda }(\mathcal {Y})\).
1.2 A.2 Circuit Classes
For a gate g we denote by \({\mathsf {type}}_C(g)\) the type of the gate g in the circuit C and by \({\mathsf {parents}}_C(g)\) the list of gates of C whose output is an input to C (such list may potentially contain duplicates).
We define the multiplicative depth of a circuit as follows:
Definition A.2
(Multiplicative Depth). Let C be a circuit, we define the multiplicative depth of C as \({\mathsf {md}}(g_{out})\) where \(g_{out}\) is its output gate and the function \({\mathsf {md}}\), from the set of gates to the set of natural numbers is recursively defined as follows:

where the sum in the last case is over the integers.
The following two circuit classes will appear in several of our results.
Definition A.3
(Circuits with Constant Multiplicative Depth). We denote by \(\mathsf {AC}^0_{\text {CM}}[2]\) the class of circuits in \(\mathsf {AC}^0[2]\) with constant multiplicative depth.
Definition A.4
(Circuits with Quasi-Constant Multiplicative Depth). For a circuit C we denote by \(S_{\omega (1)}(C)\) the set of \(\mathsf {AND}\) and \(\mathsf {OR}\) gates in C with non-constant fan-in. We say that C has quasi-constant multiplicative depth if \(|S_{\omega (1)}(C)| = O(1)\). We shall denote by \(\mathsf {AC}^0_{\text {Q}}[2]\) the class of circuits in \(\mathsf {AC}^0[2]\) with quasi-constant multiplicative depth.
1.3 A.3 Public-Key Encryption
A public-key encryption scheme
\(\mathsf {PKE}= (\mathsf {PKE.Keygen}, \mathsf {PKE.Enc}, \mathsf {PKE.Dec})\) is a triple of algorithms which operate as follow:
-
Key Generation. The algorithm \((\mathsf {pk},\mathsf {sk})\leftarrow \) \(\mathsf {PKE.Keygen}\) \((1^{\lambda })\) takes a unary representation of the security parameter and outputs a public key encryption key \(\mathsf {pk}\) and a secret decryption key \(\mathsf {sk}\).
-
Encryption. The algorithm \(c\leftarrow \) \(\mathsf {PKE.Enc}\) \(_{\mathsf {pk}}(\mu )\) takes the public key \(\mathsf {pk}\) and a single bit message \(\mu \in \{0, 1\}\) and outputs a ciphertext c. The notation \(\mathsf {PKE.Enc}\) \(_{\mathsf {pk}}(\mu ;r)\) will be used to represent the encryption of a bit \(\mu \) using randomness r.
-
Decryption. The algorithm \(\mu ^*\leftarrow \) \(\mathsf {PKE.Dec}\) \(_{\mathsf {sk}}(c)\) takes the secret key \(\mathsf {sk}\) and a ciphertext c and outputs a message \(\mu ^*\in \{0, 1\}\).
Obviously we require that \(\mu =\) \(\mathsf {PKE.Dec}\) \(_{\mathsf {sk}}(\) \(\mathsf {PKE.Enc}\) \(_{\mathsf {pk}}(\mu ))\)
Definition A.5
(CPA Security for PKE). A scheme \(\mathsf {PKE}\) is IND-CPA secure if for an infinite \(\varLambda \subseteq \mathbb {N}\) we have
where \((\mathsf {pk},\mathsf {sk})\leftarrow \) \(\mathsf {PKE.Keygen}\)(\(1^{\lambda }\)).
Remark A.1
(Security for Multiple Messages). Notice that by a standard hybrid argument and Lemma A.1 we can prove that any scheme secure according to Definition A.5 is also secure for multiple messages (i.e. the two sequences of encryptions bit by bit of two bit strings are computationally indistinguishable). We will use this fact in the constructions in Sect. 4, but we do not provide the formal definition for this type of security. We refer the reader to 5.4.2 in [Gol09].
Somewhat Homomorphic Encryption. A public-key encryption scheme is said to be homomorphic if there is an additional algorithm \(\mathsf {Eval}\) which takes a input the public key \(\mathsf {pk}\), the representation of a function \(f:\{0, 1\}^l\rightarrow \{0, 1\}\) and a set of l ciphertexts \(c_1,\ldots ,c_l\), and outputs a ciphertext \(c_f\)Footnote 19.
We proceed to define the homomorphism property. The next notion of \(\mathcal {C}\)-homomorphism is sometimes also referred to as “somewhat homomorphism”.
Definition A.6
(\(\mathcal {C}\)-homomorphism). Let \(\mathcal {C}\) be a class of functions (together with their respective representations). An encryption scheme \(\mathsf {PKE}\) is \(\mathcal {C}\)-homomorphic (or, homomorphic for the class \(\mathcal {C}\)) if for every function \(f_\lambda \) where \(f_\lambda \in \mathcal {F} \{f_{\lambda }\}_{\lambda \in \mathbb {N}} \in \mathcal {C}\) and respective inputs \(\mu _1,\dots ,\mu _n \in \{0, 1\}\) (where \(n = n(\lambda )\)), it holds that if \((\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {PKE.Keygen}(1^{\lambda })\) and \(c_i \leftarrow \mathsf {PKE.Enc}_{\mathsf {pk}}(\mu _i)\) then
As usual we require the scheme to be non-trivial by requiring that the output of \(\mathsf {Eval}\) is compact:
Definition A.7
(Compactness). A homomorphic encryption scheme \(\mathsf {PKE}\) is compact if there exists a polynomial s in \(\lambda \) such that the output length of \(\mathsf {Eval}\) is at most \(s(\lambda )\) bits long (regardless of the function f being computed or the number of inputs).
Definition A.8
Let \(\mathcal {C}= \{\mathcal {C}_{\lambda }\}_{\lambda \in \mathbb {N}}\) of arithmetic circuits in \(\text {GF}(2)\). A scheme \(\mathsf {PKE}\) is leveled \(\mathcal {C}\)-homomorphic if it takes \(1^L\) as additional input in key generation, and can only evaluate depth-L arithmetic circuits from \(\mathcal {C}\). The bound \(s(\lambda )\) on the ciphertext must remain independent of L.
1.4 A.4 Verifiable Computation
In a Verifiable Computation scheme a Client uses an untrusted server to compute a function f over an input x. The goal is to prevent the Client from accepting an incorrect value \(y'\ne f(x)\). We require that the Client’s cost of running this protocol be smaller than the cost of computing the function on his own. The following definition is from [GGP10] which allows the client to run a possibly expensive pre-processing step.
Definition A.9
(Verifiable Computation Scheme). We define a verifiable computation scheme as a quadruple of algorithms \(\mathcal{VC}= (\mathsf {VC.KeyGen},\) \(\mathsf {VC.ProbGen},\mathsf {VC.Compute},\mathsf {VC.Verify})\) where:
-
1.
\(\mathsf {VC.KeyGen}(f, 1^\lambda ) \rightarrow (\mathsf {pk}_{\mathsf {W}}, \mathsf {sk}_{\mathsf {D}})\): Based on the security parameter \(\lambda \), the randomized key generation algorithm generates a public key that encodes the target function f, which is used by the Server to compute f. It also computes a matching secret key, which is kept private by the Client.
-
2.
\(\mathsf {VC.ProbGen}_{\mathsf {sk}_{\mathsf {D}}}(x) \rightarrow (q_x,s_x)\): The problem generation algorithm uses the secret key \(\mathsf {sk}_{\mathsf {D}}\) to encode the function input x as a public query \(q_x\) which is given to the Server to compute with, and a secret value \(s_x\) which is kept private by the Client.
-
3.
\(\mathsf {VC.Compute}_{\mathsf {pk}_{\mathsf {W}}}(q_x) \rightarrow a_x\): Using the Client’s public key and the encoded input, the Server computes an encoded version of the function’s output \(y = F(x)\).
-
4.
\(\mathsf {VC.Verify}_{\mathsf {sk}_{\mathsf {D}}}(s_x,a_x) \rightarrow y \cup \{ \bot \}\): Using the secret key \(\mathsf {sk}_{\mathsf {D}}\) and the secret “decoding” \(s_x\), the verification algorithm converts the worker’s encoded output into the output of the function, e.g., \(y = f(x)\) or outputs \(\bot \) indicating that \(a_x\) does not represent the valid output of f on x.
The scheme should be complete, i.e. an honest Server should (almost) always return the correct value.
Definition A.10
(Completeness). A delegation scheme \(\mathcal{VC}\), with \(\mathcal{VC}= (\mathsf {VC.KeyGen},\mathsf {VC.ProbGen},\mathsf {VC.Compute},\mathsf {VC.Verify})\), has overwhelming completeness for a class of functions \(\mathcal {C}\) if there is a function \(\nu (n) = \mathsf {neg}(\lambda )\) such that for infinitely many values of \(\lambda \), if \(f_\lambda \in \mathcal {F} \in \mathcal {C}\), then for all inputs x the following holds with probability at least \(1-\nu (n)\): \((\mathsf {pk}_{\mathsf {W}}, \mathsf {sk}_{\mathsf {D}}) \leftarrow \mathsf {VC.KeyGen}(f_\lambda , \lambda )\), \((q_x,s_x) \leftarrow \mathsf {VC.ProbGen}_{\mathsf {sk}_{\mathsf {D}}}(x)\) and \(a_x\leftarrow \mathsf {VC.Compute}_{\mathsf {pk}_{\mathsf {W}}}(q_x)\) then \(y=f_{\lambda }(x) \leftarrow \mathsf {VC.Verify}_{\mathsf {sk}_{\mathsf {D}}}(s_x,a_x)\).
To define soundness we consider an adversary who plays the role of a malicious Server who tries to convince the Client of an incorrect output \(y \ne f(x)\). The adversary is allowed to run the protocol on inputs of her choice, i.e. see the queries \(q_{x_i}\) for adversarially chosen \(x_{i}\)’s before picking an input x and attempt to cheat on that input. Because we are interested in the parallel complexity of the adversary we distinguish between two parameters l and m. The adversary is allowed to do l rounds of adaptive queries, and in each round she queries m inputs. Jumping ahead, because our adversaries are restricted to \(\mathsf {NC}^1\) circuits, we will have to bound l with a constant, but we will be able to keep m polynomially large.

Remark A.2
In the experiment above the adversary “tries to cheat” on the last input presented in the last round of queries (i.e. \(x_{lm}\)). This is without loss of generality. In fact, assume the adversary aimed at cheating on an input presented before round l, then with one additional round it could present that same input once more as the last of the batch in that round.
Definition A.11
(Soundness). We say that a verifiable computation scheme is (l, m)-sound against a class \(\mathcal {A}\) of adversaries if there exists a negligible function \(\mathsf {neg}(\lambda )\), such that for all \(A = \{A_\lambda \}_\lambda \in \mathcal {A}\), and for infinitely many \(\lambda \) we have that
Assume the function f we are trying to compute belongs to a class \(\mathcal {C}\) which is smaller than \(\mathcal {A}\). Then our definition guarantees that the “cost” of cheating is higher than the cost of honestly computing f and engaging in the Verifiable Computation protocol \(\mathcal {VC}\). Jumping ahead, our scheme will allow us to compute the class \(\mathcal {C}=\mathsf {AC}^0[2]\) against the class of adversaries \(\mathcal {A}=\mathsf {NC}^1\).
Efficiency The last thing to consider is the efficiency of a VC protocol. Here we focus on the time complexity of computing the function f. Let n be the number of input bits, and m be the number of output bits, and S be the size of the circuit computing f.
-
A verifiable computation scheme \(\mathcal{VC}\) is client-efficient if circuit sizes of \(\mathsf {VC.ProbGen}\) and \(\mathsf {VC.Verify}\) are o(S). We say that it is linear-client if those sizes are \(O({\mathsf {poly}}(\lambda )(n + m))\).
-
A verifiable computation scheme \(\mathcal{VC}\) is server-efficient if the circuit size of \(\mathsf {VC.Compute}\) is \(O({\mathsf {poly}}(\lambda )S)\).
We note that the key generation protocol \(\mathsf {VC.KeyGen}\) can be expensive, and indeed in our protocol (as in [GGP10, CKV10, AIK10]) its cost is the same as computing f – this is OK as \(\mathsf {VC.KeyGen}\) is only invoked once per function, and the cost can be amortized over several computations of f.
B Proofs for Homomorphic Encryption Constructions
1.1 B.1 Constant Multiplicative Depth
Lemma B.1
The construction of \(\mathsf {HE}\) (Sect. 3.1) satisfies Eq. 1 (ibid).
Proof
For homomorphic addition:

where \(\mu _i\) is the plaintext corresponding to \(\mathbf {v}_i\).
For homomorphic multiplication:

where in the third and fourth equality we used respectively Eq. 1 and the definition of \(h_{i,j}\), and \(\mu , \mu '\) are the plaintexts corresponding to \(\mathbf {v}\) \(\mathbf {v}'\) respectively.
\(\square \)
Theorem B.1
(Security). The scheme \(\mathsf {HE}\) is \(\text {CPA}\) secure against \(\mathsf {NC}^1\) adversaries (Definition A.5) under the assumption \(\mathsf {NC}^1 \subsetneq \oplus \mathsf {L}/ {\mathsf {poly}}\).
Proof
We are going to prove that there exists infinite \(\varLambda \subseteq \mathbb {N}\) such that \((\mathsf {pk},\mathsf {evk}, \mathsf {HE.Enc}_{\mathsf {pk}}(0)) \sim _{\varLambda }(\mathsf {pk},\mathsf {evk}, \mathsf {HE.Enc}_{\mathsf {pk}}(1))\).
When using the notations \(\mathbf {M}^{\mathcal {\text {f}}}\) and \(\mathbf {M}^{\text {kg}}\) we will always denote matrices distributed respectively according to \(\mathcal {D}^{\text {f}}_{\lambda }\) and \(\mathcal {D}^{\text {kg}}\), where \(\mathcal {D}^{\text {f}}_{\lambda }\) and \(\mathcal {D}^{\text {kg}}\) are the distributions defined in Lemma 3.1.
We will define the (randomized) encoding procedure \(\mathsf {E}: \{0, 1\}^{\lambda \times \lambda } \rightarrow \{0, 1\}^{\lambda }\) defined as
where r is uniformly distributed in \(\{0, 1\}^{\lambda }\). The functions we will pass to \(\mathsf {E}\) will be distributed either according to \(\mathbf {M}^{\text {kg}}\) or \(\mathbf {M}^{\mathcal {\text {f}}}\). Notice that: (i) \(\mathsf {E}(\mathbf {M}^{\text {kg}}, b)\) is distributed identically to \(\mathsf {HE.Enc}_{\mathsf {pk}}(b)\); (ii) \(\mathsf {E}(\mathbf {M}^{\mathcal {\text {f}}}, b)\) corresponds to the uniform distribution over \(\{0, 1\}^{\lambda }\) because (by Lemma 3.1) \(\mathbf {M}^{\mathcal {\text {f}}}\) has full rank and hence \({\mathbf {r}}^{\intercal }\mathbf {M}^{\mathcal {\text {f}}}\) must be uniformly random.
We will denote with \(\mathbf {M}^{\text {kg}}_1, \dots , \mathbf {M}^{\text {kg}}_{L}\) the matrices \(\mathbf {M}_1, \dots , \mathbf {M}_{L}\) used to construct the evaluation key in \(\mathsf {HE.Keygen}\) (see definition). Recall these matrices are distributed according to \(\mathcal {D}^{\text {kg}}\) as in Lemma 3.1.
We will also define the following vectors:

where \(\mathbf {k}_{\ell }\) is defined as in \(\mathsf {HE.Keygen}\) and the matrices in input to \(\mathsf {E}\) will be clear from the context. Notice that all the elements of \(\mathbf {\alpha }^{\text {kg}}_{\ell }\) are encryptions, whereas all the elements of \(\mathbf {\alpha }^{\text {f}}_{\ell }\) are uniformly distributed.
We will use a standard hybrid argument. Each of our hybrids is parametrized by a bit b. This bit informally marks whether the hybrid contains an element indistinguishable from an encryption of b.
-
 where \(\mathbf {M}^{\text {kg}}_0\) corresponds to the public key of our scheme. Notice that \(\mathbf {\alpha }^{\text {kg}}_{\ell } \equiv \{ \varvec{a}_{\ell , i, j} \ | \ i,j \in [\lambda ] \}\) where \( \varvec{a}_{\ell , i, j}\) is as defined in \(\mathsf {HE.Keygen}\). This hybrid corresponds to the distribution \((\mathsf {pk},\mathsf {evk}, \mathsf {HE.Enc}_{\mathsf {pk}}(b))\).
where \(\mathbf {M}^{\text {kg}}_0\) corresponds to the public key of our scheme. Notice that \(\mathbf {\alpha }^{\text {kg}}_{\ell } \equiv \{ \varvec{a}_{\ell , i, j} \ | \ i,j \in [\lambda ] \}\) where \( \varvec{a}_{\ell , i, j}\) is as defined in \(\mathsf {HE.Keygen}\). This hybrid corresponds to the distribution \((\mathsf {pk},\mathsf {evk}, \mathsf {HE.Enc}_{\mathsf {pk}}(b))\). -
 . The only difference from \(\mathcal {E}\) is in the first two components where we replaced the actual public key and ciphertext with a full rank matrix distributed according to \(\mathcal {D}^{\text {f}}_{\lambda }\) and a random vector of bits.
. The only difference from \(\mathcal {E}\) is in the first two components where we replaced the actual public key and ciphertext with a full rank matrix distributed according to \(\mathcal {D}^{\text {f}}_{\lambda }\) and a random vector of bits. -
For \(\ell \in [L]\) we define
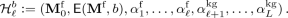
We will proceed proving that
through a series of smaller claims. In the remainder of the proof \(\varLambda \) refers to the set in Lemma 3.1.
-
\(\mathcal {E}^{0}\sim _{\varLambda }\mathcal {H}^{0}_0\): if this were not the case we would be able to distinguish \(\mathbf {M}^{\text {kg}}_0\) from \(\mathbf {M}^{\mathcal {\text {f}}}_0\) for some of the values in the set \(\varLambda \) thus contradicting Lemma 3.1.
-
\(\mathcal {H}^{0}_{\ell -1} \sim _{\varLambda }\mathcal {H}^{0}_{\ell }\) for \(\ell \in [L]\): assume by contradiction this statement is false for some \(\ell \in [L]\). That is
$$\begin{aligned}&(\mathbf {M}^{\mathcal {\text {f}}}_0, \mathsf {E}(\mathbf {M}^{\mathcal {\text {f}}}_0, b), \mathbf {\alpha }^{\text {f}}_1, \dots , \mathbf {\alpha }^{\text {f}}_{\ell -1}, \mathbf {\alpha }^{\text {kg}}_{\ell }, \dots , \mathbf {\alpha }^{\text {kg}}_L)&\\&\qquad \qquad \qquad \qquad \not \sim _{\varLambda }&\\&(\mathbf {M}^{\mathcal {\text {f}}}_0, \mathsf {E}(\mathbf {M}^{\mathcal {\text {f}}}_0, b), \mathbf {\alpha }^{\text {f}}_1, \dots , \mathbf {\alpha }^{\text {f}}_{\ell }, \mathbf {\alpha }^{\text {kg}}_{\ell +1}, \dots , \mathbf {\alpha }^{\text {kg}}_L)&\, \end{aligned}$$Recall that, by definition, the elements of \(\mathbf {\alpha }^{\text {kg}}_{\ell }\) are all encryptions whereas the elements of \(\mathbf {\alpha }^{\text {f}}_{\ell }\) are all randomly distributed values. This contradicts the semantic security of the scheme \(\mathsf {PKE}\) (by a standard hybrid argument on the number of ciphertexts).
-
\(\mathcal {H}^{0}_{L} \sim _{\varLambda }\mathcal {H}^1_{L}\): the distributions associated to these two hybrids are identical. In fact, notice the only difference between these two hybrids is in the second component: \(\mathsf {E}(\mathbf {M}^{\mathcal {\text {f}}}, 0)\) in \(\mathcal {H}^{0}_{L}\) and \(\mathsf {E}(\mathbf {M}^{\mathcal {\text {f}}}, 1)\) in \(\mathcal {H}^1_{L}\). As observed above \(\mathsf {E}(\mathbf {M}^{\mathcal {\text {f}}}, b)\) is uniformly distributed, which proves the claim.
All the claims above can be proven analogously for \(\mathcal {E}^1, \mathcal {H}^1_{0}\) and \(\mathcal {H}^1_{\ell }\)-s.
\(\square \)
1.2 B.2 Quasi-constant Multiplicative Depth
Lemma B.2
([Raz87]). Let C be an \(\mathsf {AC}^0_{\text {Q}}[2]\) circuit of depth d. Then there exists a randomized circuit \(C' \in \mathsf {AC}^0_{\text {CM}}[2]\) such that, for all x,
where \(\epsilon = O(1)\). The circuit \(C'\) uses O(n) random bits and its representation can be computed in \(\mathsf {NC}^0\) from a representation of C.
Proof
Consider a circuit \(C \in \mathsf {AC}^0_{\text {Q}}[2]\) and let \(K = O(1)\) be the total number of \(\mathsf {AND}\) and \(\mathsf {OR}\) gates with non-constant fan-in. We can replace every \(\mathsf {OR}\) gate of fan-in \(m = \omega (1)\) with a randomized “gadget” that takes in input m additional random bits and computes the function

This function can be implemented in constant multiplicative depth with one \(\mathsf {XOR}\) gate and m \(\mathsf {AND}\) gates of fan-in two. Let \(\mathbf {x} = (x_1,\dots ,x_m)\) and \(\mathbf {r} = (r_1,\dots , r_m)\). The probabilistic gadget \(\hat{g}_{\mathsf {OR}}\) has one-sided error. if \(x_i = 0\) (i.e. if \(\mathsf {OR}(\mathbf {x}) = 0\)) then \(\Pr [\hat{g}_{\mathsf {OR}}(\mathbf {x}; \mathbf {r}) = 0] = 1\); otherwise \(\Pr [\hat{g}_{\mathsf {OR}}(\mathbf {x}; \mathbf {r}) = 1] = \frac{1}{2}\).
In a similar fashion, we can replace every unbounded fan-in \(\mathsf {AND}\) gate with a randomized gadget in computing

This gadget can also be implemented in constant-multiplicative depth and has one-sided error 1 / 2. Finally, by applying the union bound we can observe that \(\Pr [C'(x) \not = C(x)] \le \epsilon \) for a constant \(\epsilon \), because we have only a constant number of gates to be replaced with gadgets for \(\hat{g}_{\mathsf {OR}}\) or \(\hat{g}_{\mathsf {AND}}\).
We only provide the intuition for why the transformations above can be carried out in \(\mathsf {NC}^0\). Assume the encoding of a circuit as a list of gates in the form \((g, t_g, in_1, \dots , in_m)\) where g and t are respectively the index of the output wire of the gate and its type (possibly of the form “input” or “random input”) and the \(in_i\)-s are the indices of the input wire of g. The transformation from C to \(C'\) needs to simply copy all the items in the list except for the gates of unbounded fan-in. We will assume the encoding conventions of C always puts these gates at the end of the listFootnote 20. For each of such gates the transformation circuit needs to: add appropriate \(r_1,\dots , r_m\) to the list, add m \(\mathsf {AND}\) gates and one \(\mathsf {XOR}\), possibly (if we are transforming an \(\mathsf {AND}\) gate) add negation gates. All this can be carried out based on wire connections and the type of the gate (a constant-size string) and thus in \(\mathsf {NC}^0\).
\(\square \)
In the construction above, we built \(C'\) by replacing every gate \(g \in {\mathsf {S}}_{\omega (1)}(C)\) (as in Definition A.4) with a (randomized) gadget \(G_g\). The output of each of these gadgets will be useful in order to keep the low complexity of the decryption algorithm in our next homomorphic encryption scheme. We shall use an “expanded” version of \(C'\), the multi-output circuit \(C'_{exp}\).
Definition B.1
(Expanded Approximating Function). Let C be a circuit in \(\mathsf {AC}^0_{\text {Q}}[2]\) and let \(C'\) be a circuit as in the proof of Lemma B.2. We denote by \(G_g(\mathbf {x}; \mathbf {r})\) the output of the gadget \(G_g\) when \(C'\) is evaluated on inputs \((\mathbf {x}; \mathbf {r})\). On input \((\mathbf {x}; \mathbf {r})\), the multi-output circuit \(C'_{exp}\) output \(C'(\mathbf {x};\mathbf {r})\) together with the outputs of the O(1) gadgets \(G_g\) for each \(g \in {\mathsf {S}}_{\omega (1)}(C)\). Finally, we denote with \(\mathsf {GenApproxFun}\) the algorithm computing a representation of \(C'_{exp}\) from a representation of C.
Lemma B.3
There exists a deterministic algorithm \({\mathsf {DecodeApprox}}\) computable in \(\mathsf {AC}^0[2]\) with the following properties. For every circuit C in \(\mathsf {AC}^0_{\text {Q}}[2]\) computing the function f, there exists \(\mathbf {aux}_f\in \{0, 1\}^{O(1)}\) such that for all \(\mathbf {x} \in \{0, 1\}^n\)
where \(C'\) is an approximating circuit as in Lemma B.2, the probability is taken over the uniformly distributed bit vectors \(\mathbf {r}^{(i)}\)-s for \(i \in [s]\), \(C'_{exp}\) is as in Definition B.1. Finally, there exists a function \({\mathsf {GenDecodeAux}}\) that computes \(\mathbf {aux}_f\) from a representation of C in \(\mathsf {NC}^0\).
Proof
Before we provide a construction for \({\mathsf {DecodeApprox}}\), let us observe how we can amplify the error of \(C'\). Consider for example a gadget \(\hat{g}_{\mathsf {OR}}\) constructed as in the proof of Lemma B.2, approximating an \(\mathsf {OR}\) gate in C. If we repeat the execution of the gadget s times, every time using fresh random bit vectors \(\mathbf {r}'^{(1)},\dots , \mathbf {r}'^{(s)}\), then we can correctly compute \(\mathsf {OR}(\mathbf {x}')\) with overwhelming probability. Define
 . Clearly \(\Pr [h_{\mathsf {OR}}(\mathbf {x}'; \mathbf {r}'^{(1)},\dots , \mathbf {r}'^{(s)}) = \mathsf {OR}(\mathbf {x}')] \ge 1 - 2^{-s}\). In a similar fashion we can define
. Clearly \(\Pr [h_{\mathsf {OR}}(\mathbf {x}'; \mathbf {r}'^{(1)},\dots , \mathbf {r}'^{(s)}) = \mathsf {OR}(\mathbf {x}')] \ge 1 - 2^{-s}\). In a similar fashion we can define
 .
.
If \(C'\) were composed by a single gadget \(\hat{g}_{\mathsf {OR}}\) (resp. \(\hat{g}_{\mathsf {AND}}\)) we could just let \({\mathsf {DecodeApprox}}\) be the same as \(h_{\mathsf {OR}}\) (resp. \(h_{\mathsf {AND}}\)) and we would be done. To deal with multiple gadgets, however, we need a more general approach. Consider some ordering on the gates in \({\mathsf {S}}_{\omega (1)}\), i.e. let \({\mathsf {S}}_{\omega (1)} = \{g_1, \dots , g_K\}\). For sake of presentation, assume there are only gadgets approximating \(\mathsf {OR}\) gates and let us temporarily ignore \(\mathbf {aux}_f\). We can write each of the \(C'_{exp}(\mathbf {x}; \mathbf {r}^{(j)})\) input to \({\mathsf {DecodeApprox}}\) as \((z^{(j)}, y_1^{(j)}, \dots , y_K^{(j)})\) where \(z^{(j)}\) is the output of \(C'(\mathbf {x}, \mathbf {r}^{(j)})\) and \(y_i^{(j)}\) is the output of the gadget corresponding to \(g_i\) when provided random bits from \(\mathbf {r}^{(j)}\). Define \(y_i^*\) as
 . We then let the output of \({\mathsf {DecodeApprox}}\) be \(z^{\hat{j}}\) where \(\hat{j}\) is such that for all \(i \in [K]\) it is the case that \(y_i^{(\hat{j})} = y_i^*\). We let \({\mathsf {DecodeApprox}}\) output an arbitrary value if such \(\hat{j}\) does not exist. However we can prove (Lemma B.4) that \(\hat{j}\) exists with overwhelming probability. Denote by \(V_{C,\mathbf {x}}(g_i)\) the value of the output wire of \(g_i\) when evaluating C on input \(\mathbf {x}\). Clearly, by construction of \(C'_{exp}\), \(\Pr [z^{(\hat{j})} = C(\mathbf {x})] \ge \Pr [ \forall i \ y_i^{(\hat{j})}= V_{C,\mathbf {x}}(g_i)]\) and by the proof of Lemma B.4 we can show that the right hand side probability is overwhelming.
. We then let the output of \({\mathsf {DecodeApprox}}\) be \(z^{\hat{j}}\) where \(\hat{j}\) is such that for all \(i \in [K]\) it is the case that \(y_i^{(\hat{j})} = y_i^*\). We let \({\mathsf {DecodeApprox}}\) output an arbitrary value if such \(\hat{j}\) does not exist. However we can prove (Lemma B.4) that \(\hat{j}\) exists with overwhelming probability. Denote by \(V_{C,\mathbf {x}}(g_i)\) the value of the output wire of \(g_i\) when evaluating C on input \(\mathbf {x}\). Clearly, by construction of \(C'_{exp}\), \(\Pr [z^{(\hat{j})} = C(\mathbf {x})] \ge \Pr [ \forall i \ y_i^{(\hat{j})}= V_{C,\mathbf {x}}(g_i)]\) and by the proof of Lemma B.4 we can show that the right hand side probability is overwhelming.
To generalize this same approach to the scenario including both \(\mathsf {OR}\) and \(\mathsf {AND}\) gadgets we let the string \(\mathbf {aux}_f\) include information on the type of gates in \({\mathsf {S}}_{\omega (1)}\). This way \({\mathsf {DecodeApprox}}\) can use \(\hat{g}_{\mathsf {OR}}\) or \(\hat{g}_{\mathsf {AND}}\) accordingly. Clearly the representation of \(\mathbf {aux}_f\) can be computed by a representation of C in \(\mathsf {NC}^0\).
\(\square \)
Lemma B.4
\( \Pr [\exists \hat{j}\ \forall i \ y_i^{(\hat{j})}= y_i^*] \ge 1 - \mathsf {neg}(s)\).
Proof
Let \({\mathsf {S}}_{\omega (1)} = \{g_1, \dots , g_K\}\) and \(V_{C,\mathbf {x}}(g_i)\) for \(i \in [K]\) defined as in the proof of Lemma B.3. We have that
We now bound each of the two probabilities in the last product. Denote by \(\mathcal {E}_{i,j}\) the event \(``y_i^{(j)}= V_{C,\mathbf {x}}(g_i)"\) and by \(\overline{\mathcal {E}}_{i,j}\) its negation. Observe that
Remark B.1
(Efficiency of \(\mathsf {HE}'\) in Sect. 3.3). Given in input a function f not necessarily of constant multiplicative depth, \(\mathsf {GenApproxFun}\) returns a function \(f'\) of constant multiplicative depth that approximates it. As stated in Lemma B.2, \(\mathsf {GenApproxFun}\) is computable in \(\mathsf {NC}^0\) and so is \({\mathsf {GenDecodeAux}}\). The function \(\mathsf {SampleAuxRandomness}\) in \(\mathsf {AC}^0_{\text {CM}}[2]\) and \(\mathsf {EvalApprox}\) makes parallel invocations to \(\mathsf {HE.Eval}\) which is computable in \(\mathsf {AC}^0_{\text {CM}}[2]\) when provided in input a function in \(\mathsf {AC}^0_{\text {CM}}[2]\) (Theorem 3.3). This fact will be useful when showing the completeness of the verifiable computation constructions in Sect. 4.
C Proofs for Verifiable Computation Constructions
The following two auxiliary lemmas guarantee that the constructions in Figs. 2 and 3 are computable in \(\mathsf {AC}^0[2]\). We refer the reader to [Hag91, MV91] for the proof Lemma C.1.
Lemma C.1
[Hag91, MV91] There are uniform \(\mathsf {AC}^0\) circuits \(C: \{0, 1\}^{{\mathsf {poly}}(l)}\rightarrow [l]^l\) of size \({\mathsf {poly}}(l)\) and depth O(1) whose output distribution have statistical distance \(\le 2^{-l}\) from the uniform distribution over permutations of [l].
Lemma C.2
There are uniform \(\mathsf {AC}^0[2]\) circuits \(C: [l]^l \times \{0, 1\}^l \rightarrow \{0, 1\}^l\) of size \(O(l^2)\) where \(C(\pi , (x_1,\dots , x_l)) = (\pi (1),\dots ,\pi (l))\) and \(\pi \) is a permutation.
Proof
Let \(\mathbf {x} = (x_1,\dots ,x_l)\) the bits to permute and let \(\pi \) be a permutation If \(\pi \) is represented as a permutation matrix with rows \(\mathbf {r}_1,\dots ,\mathbf {r}_l\), we can permute \(\mathbf {x}\) by simply performing l parallel inner products \(\langle \mathbf {x} \, , \mathbf {r}_i \rangle \)-s, which is in \(\mathsf {AC}^0[2]\). We now describe how to generate the permutation matrix from a binary representations \(x_1,\dots ,x_{\mathsf {lg}(l)}\) of the integers in [l]. Let \(f_i : \{0, 1\}^{\mathsf {lg}(l)} \rightarrow \{0, 1\}^l\) be the function that computes the i-th row of the permutation matrix. We can define \(f_i\) as follows:

where \([i-1]_2\) is the binary representation of \(i-1\) and \(\mathsf {eq}\) returns 1 if its two inputs (each of lenght \(\mathsf {lg}(l)\)) are equal. The function \(f_i\) is clearly in \(\mathsf {AC}^0[2]\).
\(\square \)
1.1 C.1 One-time scheme
Remark C.1
(On deterministic homomorphic evaluation). As pointed out in [CKV10], one requirement for the approach in Fig. 2 to work is for the homomorphic evaluation to be deterministic. We point out that once \({\mathbf {\hat{r}}_{\text {aux}}}\) are fixed once and for all the homomorphic evaluation in \(\mathsf {VC.Compute}\) is deterministic.
Lemma C.3
(Completeness of \(\mathcal{VC}\)). The verifiable computation scheme \(\mathcal{VC}\) in Fig. 2 has overwhelming completeness (Definition A.10) for the class \(\mathsf {AC}^0_{\text {Q}}[2]\).
Proof
The proof is straightforward and stems directly from the homomorphic properties of \(\mathsf {HE'}\) (Theorem 3.4). In fact, by construction and by definition of \(\mathsf {HE'}\) (Sect. 3.3), the distribution of the \(\hat{w}_i\)-s is identical to \(\mathsf {HE'.Eval}_{\mathsf {pk}}(f, \hat{r}_i)\). Analogously, the distribution of \(\hat{y}_i\)-s is identical to \(\mathsf {HE'.Eval}_{\mathsf {pk}}(f, \hat{z}_i)\).
\(\square \)
Lemma C.4
(One-time Soundness). Under the assumption that \(\mathsf {NC}^1 \subsetneq \oplus \mathsf {L}/ {\mathsf {poly}}\) the scheme in Fig. 2 is (1, 1)-sound (one time secure) against \(\mathsf {NC}^1\) adversaries whenever t is chosen to be \(\omega (\log (\lambda ))\).
Proof
We follow the same proof structure as in the proof of Lemma 12 in [CKV10]. We will keep part of the analysis informal, emphasizing why this proof still works for low-depth circuits. We refer the reader to [CKV10] for further details.
The following observation will be crucial in the rest of the proof. Notice that, by construction and by definition of \(\mathsf {HE'}\) (Sect. 3.3), the distribution of the \(\hat{w}_i\)-s is identical to \(\mathsf {HE'.Eval}_{\mathsf {pk}}(f, \hat{r}_i)\). Analogously, the distribution of \(\hat{y}_i\)-s is identical to \(\mathsf {HE'.Eval}_{\mathsf {pk}}(f, \hat{z}_i)\).
Consider an \(\mathsf {NC}^1\) adversary \(\mathcal {A}^*\) that cheats with non-negligible probability in the one-time security experiment \(\mathbf{Exp}^{\mathsf {Verif}}_{A}[\mathcal{VC}, f, \lambda , 1,1]\) (Definition A.11). Let \((\hat{r}_1,\dots ,\hat{r}_{t})\) be the independent copies of \(\mathsf {HE'.Enc}_{\mathsf {pk}_{\mathsf {W}}}(\bar{0})\) and \((\hat{r}_{t+1},\dots ,\hat{r}_{2t})\) the t independent copies of \(\mathsf {HE'.Enc}_{\mathsf {pk}_{\mathsf {W}}}(x)\) as above. Whenever the verification algorithm accepts, the adversary must have responded correctly on \(\hat{r}_1,...,\hat{r}_t\) and incorrectly (and consistently) on \(\hat{r}_{t+1},\dots ,\hat{r}_{2t}\). Our goal is to bound the probability that the adversary succeeds in doing that.
First, notice that the view of the adversary is \((\mathsf {pk}_{\mathsf {W}}, \hat{r}_1,\dots ,\hat{r}_{2t})\), and identical to \((\mathsf {pk}_{\mathsf {W}}, \mathsf {HE'.Enc}_{\mathsf {pk}_{\mathsf {W}}}(\bar{0})^t, \mathsf {HE'.Enc}_{\mathsf {pk}_{\mathsf {W}}}(x)^t)\). By semantic security of the homomorphic encryption scheme, there exists an infinitely large set of parameters \(\varLambda \) such that \( (\mathsf {pk}_{\mathsf {W}}, \mathsf {HE'.Enc}_{\mathsf {pk}_{\mathsf {W}}}(\bar{0})^t, \mathsf {HE'.Enc}_{\mathsf {pk}_{\mathsf {W}}}(x)^t) \sim _{\varLambda }(\mathsf {pk}_{\mathsf {W}}, \mathsf {HE'.Enc}_{\mathsf {pk}_{\mathsf {W}}}(\bar{0})^{2t})\). Consider a modified game where the adversary receives \((\mathsf {pk}_{\mathsf {W}}, \mathsf {HE'.Enc}_{\mathsf {pk}_{\mathsf {W}}}(\bar{0})^{2t})\). Denote by p the probability that the adversary succeeds in this game. By computational indistinguishability we have
for all \(\lambda \in \varLambda \). This inequality holds because we can test in \(\mathsf {NC}^1\) whether \(\mathcal {A}^*\) cheats only on \((\hat{r}_{t+1},\dots ,\hat{r}_{2t})\). Therefore, if the adversary’s behavior differed significantly between the two games, one would be able to break the semantic security of the homomorphic scheme. Here we made use of the third fact in Lemma A.1.
We now proceed to upper bound p. Observe that
where the \(\hat{z}_{\pi (i)}\)-s are defined as in Fig. 2. Because of Lemma C.1 that the distribution of \(\pi \) is statistically indistinguishable from that of a uniformly random permutation. Also, observe that the answers \(\hat{y}_i\) of the adversary are independent of \(\pi \). We can then conclude that \(p \le \frac{1}{\left( {\begin{array}{c}2t\\ t\end{array}}\right) } + \mathsf {neg}(t)\), which concludes the security analysis.
\(\square \)
1.2 C.2 Reusable scheme
The following is a proof of the completeness of \(\overline{\mathcal{VC}}\).
Proof (Of Theorem 4.1)
The completeness of the reusable scheme follows directly from the completeness of the one-time scheme \(\mathcal{VC}\) and the homomorphic properties of \(\mathsf {HE}\). Notice that we can use \(\mathsf {HE.Eval}\) to homomorphically compute \(\mathsf {VC.Compute}\) as the latter carries out a computation in \(\mathsf {AC}^0_{\text {CM}}[2]\) (although it is approximating a computation in \(\mathsf {AC}^0_{\text {Q}}[2]\)).
\(\square \)
The following is a restatement of Theorem 4.2.
Theorem C.1
(Many-Times Soundness). Under the assumption that \(\mathsf {NC}^1 \subsetneq \oplus \mathsf {L}/ {\mathsf {poly}}\) the scheme \(\overline{\mathcal{VC}}\) in Fig. 3 is \((O(1),{\mathsf {poly}}(\lambda ))\)-sound (many-times secure) against \(\mathsf {NC}^1\) adversaries whenever t is chosen to be \(\omega (\log (\lambda ))\) in the underlying scheme \(\mathcal{VC}\).
Proof
By Lemma C.4 there exists an infinite set \(\varLambda \subseteq \mathbb {N}\) of security parameters for which \(\mathcal{VC}\) “is secure”. By the proof of Lemma C.4, this set is also the set of parameters where the somewhat homomorphic encryption scheme \(\mathsf {HE}\) “is secure”. We will show that for all values in this same set \(\varLambda \), the probability of success of any \(\mathsf {NC}^1\) adversary in \(\mathbf{Exp}^{\mathsf {Verif}}_{A}[\overline{\mathcal{VC}}, f, \lambda , O(1), {\mathsf {poly}}(\lambda )]\) is negligible.
Assume by contradiction there exists an \(\mathsf {NC}^1\) adversary \(\mathcal {A}^*\) that achieves non-negligible advantage in \(\mathbf{Exp}^{\mathsf {Verif}}_{A}[\overline{\mathcal{VC}}, f, \lambda , O(1), {\mathsf {poly}}(\lambda )]\) for some \(\lambda \in \varLambda \).
Claim: If \(\overline{\mathcal{VC}}\) is not secure for some \(\lambda ^* \in \varLambda \) then we can break the one-time security of \(\mathcal{VC}\). Let \(l = O(1)\) be the number of rounds in the many-time soundness experiment for \(\overline{\mathcal{VC}}\). Consider the following \(\mathsf {NC}^1\) adversary \(\mathcal {A}_1\) for the experiment \(\mathbf{Exp}^{\mathsf {Verif}}_{A}[\mathcal{VC}, f, \lambda , 1,1]\):
-
\(\mathcal {A}_1\) obtains a pair a public key \(\mathsf {pk}_{\mathsf {W}}\) and sends it to \(\mathcal {A}^*\);
-
For all rounds \(i \in \{1,\dots ,l-1 \}\), \(\mathcal {A}_1\) replies to \(\mathcal {A}^*\) queries by generating a fresh pair of keys \((\mathsf {pk}, \mathsf {sk})\) and sending back encryptions of \(\mathsf {HE.Enc}_{\mathsf {pk}}(\bar{0})\);
-
At round l, \(\mathcal {A}_1\) responds to all input queries but the last one as above. This, by experiment definition, is the input where \(\mathcal {A}^*\) will try to cheat; we denote this input by \(x^*\). Now \(\mathcal {A}_1\) sends \(x^*\) as the only input query in the one-time security experiment and will receive back \(q^*\). It will then obtain a fresh pair of keys \((\mathsf {pk}^*, \mathsf {sk}^*)\) and send \(\mathsf {HE.Enc}_{\mathsf {pk}^*}(q^*)\) to \(\mathcal {A}^*\).
-
\(\mathcal {A}^*\) will respond with \(\hat{a}^*\) and \(\mathcal {A}_1\) will send \(\mathsf {HE.Dec}_{\mathsf {sk}^*}(\hat{a})\) to the challenger for one-time security experiment.
The advantage of \(\mathcal {A}_1\) depends on how likely is \(\mathcal {A}^*\) can successfully cheat in that interaction. Let p be the advantage of \(\mathcal {A}_1\) in the one-time security experiment. Clearly, if p is close to the advantage of \(\mathcal {A}^*\) in the many-times security experiment \(\mathcal {A}_1\) breaks the security of the one-time scheme.
Claim: the advantage of \(\mathcal {A}_1\) is negligibly close to that of \(\mathcal {A}^*\) in the many-time security game for security parameter \(\lambda ^*\). We can prove this by relying on the semantic security of the homomorphic encryption and on a hybrid argument.
Let \(L = lm\), the total number of input queries in the many-times security experiment. We now define the hybrids \(H^{(j)}\) with \(j \in \{0, \dots , L\}\). We define \(H^{(0)}\) to be the exactly the many-time security experiment. For \(j \in [L]\) we define \(H^{(j)}\) to be an experiment where we respond to input queries with \(\mathsf {HE.Enc}_{\mathsf {pk}_f}(\bar{0})\) where \(\mathsf {pk}_f\) is a fresh public key up to input query j and behaves the many-time security experiment from input query \(j+1\) on. Notice that \(H^{(L)}\) corresponds to the interaction with \(\mathcal {A}_1\) above.
Denote by \(A^{(j)}\) the output distribution of \(\mathcal {A}^*\) when interacting with \(H^{(j)}\). Intuitively, if the advantage of the \(\mathcal {A}_1\) in the one-time experiment is significantly different from the advantage of \(\mathcal {A}^*\) in the many-times security games, then \(A^{(0)}\) and \(A^{(L)}\) are not \(\varLambda \)-computationally indistinguishable. Therefore (by Lemma A.1), there exists \(j \in [L]\) such that \(A^{(j-1)} \not \sim _{\varLambda } A^{(j)}\).
Claim: If there exists \(j \in [L]\) such that \(A^{(j-1)} \not \sim _{\varLambda } A^{(j)}\) then we can break the semantic security of \(\mathsf {HE}\). Consider the following \(\mathsf {NC}^1\) adversary \(\mathcal {A}_{\text {CPA}}\) which receives in input a “challenge” public key \(\mathsf {pk}^*\). \(\mathcal {A}_{\text {CPA}}\) will interact with \(\mathcal {A}^*\) simulating \(H^{(j)}\) until receiving input query \(x_{j}\). At this point it will compute \(q_j\) from \(\mathsf {VC.ProbGen}(x_j)\) and send to the CPA challenger (see Remark A.1) \(q_j\) and \(\bar{0}\), receiving back an encryption \(c^*\) of either message under the public key \(\mathsf {pk}^*\). \(\mathcal {A}_{\text {CPA}}\) will now send \((\mathsf {pk}^*, c^*)\) to \(\mathcal {A}^*\) and continue simulating \(H^{(j)}\) till the end of the experiment. The adversary \(\mathcal {A}_{\text {CPA}}\) will check whether \(\mathcal {A}^*\) cheated successfully at the end of the experiment and output (in the multiple-message CPA experiment) 1 if that is the case and 0 otherwise. This would allow \(\mathcal {A}_{\text {CPA}}\) to have a noticeable advantage in the experiment thus breaking the semantic security of \(\mathsf {HE}\).
\(\square \)
D On Approaches Based on Randomized Encodings
A randomized encoding of a function f is a randomized function \(\hat{f}\) such that for any input x, the distribution of \(\hat{f}(x)\) reveals f(x), but nothing more about x. We observe that approaches based on low-depth information-theoretic affine randomized encodings (as constructed in [IK00a, IK02, AIK04] or as applied in [SYY99, AIK10, GGH+07]) may be used to obtain results similar to ours. Known ways to construct these tools, however, all seem to have significant limitations, which pushed us to look for different solutions.
Example Constructions. An example construction for homomorphic encryption: the encryptor could send to the evaluator a linearly homomorphic encryption of the inputs and the evaluator could reply with an affine (requiring only linear operations) randomized encoding of f computed on the ciphertexts. Possible constructions for verifiable computation could be based on [AIK10] or using a constant-round variant of [GKR08] for \(\mathsf {NC}^1\) circuits together with the approach in [GGH+07].
Limitations of constructions from RE. Such approaches can yield homomorphic encryption for \(\mathsf {NC}^1\) circuits and verifiable computation in low-depth. Noticeably, such schemes would be (partly) implementable in \(\mathsf {NC}^0\) and the soundness of the (one-time) verifiable computation could hold unconditionally.
In our work, however, we are interested in compact homomorphic encryption schemes (where the ciphertexts do not grow in size with each homomorphic operation) and in verifiable computation schemes where the total (online) work of the verifier is approximately linear in the I/O sizeFootnote 21. When using currently known constructions the techniques mentioned above seem to fail in both respects. One reason for this is that having the verifier (resp. evaluator) compute (resp. send) an information-theoreticFootnote 22 randomized encoding would require verification time (resp. communication complexity) to be at best \(\varOmega (n^2)\) (resp. \(\varOmega (2^d)\), where d is the depth of the fan-in two evaluation circuit). These lower bounds refer to the complexity of known constructions for information-theoretic randomized encodings [AIK04], which stem from two main approaches: the branching-program based one in [IK00a] and the “Yao-like” in [IK02] (Sect. 3). The former constructs randomized encodings computable in time \(\varOmega (\ell ^2)\) and of the same size, where \(\ell \) is the size of the (polynomial-size) branching program describing f (the related approach in [GGH+07] has output size and computation time of \(\ell ^3\)). The latter describes randomized encodings of size \(2^d\) and computable in \(s^2\) for circuits of size s and (logarithmic) depth d. The complexity of these encodings can be improved under the existence of PRGs with linear stretch (e.g. [AIK10] uses this fact to build verifiable computation with low online communication). Unfortunately it is not known how to build such primitives under the assumption \(\mathsf {NC}^1 \subsetneq \oplus \mathsf {L}/ {\mathsf {poly}}\) [DVV16].
It would be worth investigating exactly the extent to which we can exploit such techniques in a context where low communication complexity and low sequential verification complexity are not constraints. We leave this as an open problem. We finally point out that some of these depth-reduction techniques can be applied to our results (naturally, with overheads similar to the ones pointed out above).
Rights and permissions
Copyright information
© 2018 International Association for Cryptologic Research
About this paper
Cite this paper
Campanelli, M., Gennaro, R. (2018). Fine-Grained Secure Computation. In: Beimel, A., Dziembowski, S. (eds) Theory of Cryptography. TCC 2018. Lecture Notes in Computer Science(), vol 11240. Springer, Cham. https://doi.org/10.1007/978-3-030-03810-6_3
Download citation
DOI: https://doi.org/10.1007/978-3-030-03810-6_3
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-03809-0
Online ISBN: 978-3-030-03810-6
eBook Packages: Computer ScienceComputer Science (R0)






 to be the set of all these values. t then outputs the secret key
to be the set of all these values. t then outputs the secret key  .
.


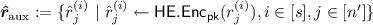 ;
;
 where
where  . The only difference from
. The only difference from