Think Before You Discard: Accurate Triangle Counting in Graph Streams with Deletions

Abstract

Given a stream of edge additions and deletions, how can we estimate the count of triangles in it? If we can store only a subset of the edges, how can we obtain unbiased estimates with small variances?

Counting triangles (i.e., cliques of size three) in a graph is a classical problem with applications in a wide range of research areas, including social network analysis, data mining, and databases. Recently, streaming algorithms for triangle counting have been extensively studied since they can naturally be used for large dynamic graphs. However, existing algorithms cannot handle edge deletions or suffer from low accuracy.

Can we handle edge deletions while achieving high accuracy? We propose ThinkD, which accurately estimates the counts of global triangles (i.e., all triangles) and local triangles associated with each node in a fully dynamic graph stream with edge additions and deletions. Compared to its best competitors, ThinkD is (a) Accurate: up to 4.3${\times }$ more accurate within the same memory budget, (b) Fast: up to 2.2${\times }$ faster for the same accuracy requirements, and (c) Theoretically sound: always maintaining unbiased estimates with small variances. Code related to this paper is available at: https://github.com/kijungs/thinkd.

1 Introduction

Given a fully dynamic graph stream with edge additions and deletions, how can we accurately estimate the count of triangles in it with fixed memory size?

The count of triangles (i.e., cliques of size three) is a key primitive in graph analysis with a wide range of applications, including spam/anomaly detection [5, 14], link recommendation [8, 22], community detection [6], degeneracy estimation [18], and query optimization [3]. In particular, many important metrics in social network analysis, including the clustering coefficient [24], the transitivity ratio [15], and the triangle connectivity [4], are based on the count of triangles.

Many real graphs are best represented as a sequence of edge additions and deletions, and they often need to be processed in real time. For example, many social networking service companies aim to detect fraud or spam as quickly as possible in their online social networks, which evolve indefinitely with both edge additions and deletions. Another example is to examine graphs of data traffic and improve the network performance in real time.

Table 1. Comparison of streaming algorithms for triangle counting. Notice that ThinkD is accurate while satisfying all the criteria.

As a result, there has been great interest in graph stream algorithms, which gradually update their outputs as each edge insertion or deletion is received rather than operating on the entire graph at once. However, existing streaming algorithms for triangle counting focus on insertion-only streams [2, 11, 14, 16, 17, 19] or greatly sacrifice accuracy to support edge deletions [7, 10, 13].

In this work, we propose ThinkD (Think before you Discard), an accurate streaming algorithm for triangle counting in a fully dynamic graph stream with both edge additions and deletions. ThinkD maintains and updates estimates of the counts of global triangles (i.e., all triangles) and local triangles incident to each node. ThinkD is named after the fact that, upon receiving each edge addition or deletion, ThinkD uses it to improve its estimates even if the edge is about to be discarded without being stored. This allows ThinkD to achieve higher accuracy than if it were to only use edges in memory for estimation. As a result, our proposed algorithm ThinkD has the following strengths:

• Accurate: ThinkD gives up to 4${\times }$ and 4.3${\times }$ smaller estimation errors for global and local triangle counts, respectively, than its best competitors within the same memory budget (Fig. 2).

• Fast: ThinkD scales linearly with the size of the input stream (Fig. 1, Corollary 1, and Theorem 4). Especially, ThinkD is up to 2.2${\times }$ faster than its best competitors with similar accuracies (Fig. 3).

• Theoretically Sound: We prove the formulas for the bias and variance of the estimates provided by ThinkD (Theorems 1 and 2). In particular, we show that ThinkD always maintains unbiased estimates (Fig. 1).

Reproducibility: The source code and datasets used in the paper are available at http://www.cs.cmu.edu/~kijungs/codes/thinkd/.

In Sect. 2, we review related work. In Sect. 3, we present notations and the problem definition. In Sect. 4, we describe our proposed algorithm ThinkD. After providing experimental results in Sect. 5, we conclude in Sect. 6.

Table 2. Table of frequently-used symbols.

2 Related Work

See Table 1 for a comparison of streaming algorithms for triangle counting. Streaming algorithms for triangle counting in insertion-only graph streams have been studied extensively, including multi-pass [12, 21] or single-pass [2, 11, 16, 20] algorithms for the count of global triangles, and multi-pass [5] or single-pass [7, 14, 17, 19] algorithms for the counts of both global and local triangles.

The first algorithm for triangle counting in fully dynamic graph streams with edge deletions was proposed in [13]. The algorithm estimates the count of global triangles by making a single pass over the input stream. However, the algorithm is inapplicable to real-time applications since it expensively computes an estimate once at the end of the stream instead of always maintaining an estimate. Although ESD [10] maintains and updates an estimate of the global triangle count, its scalability is limited since it requires the entire input graph to be stored in memory. Triest_fd [7], which maintains and updates estimates of both global and local triangle counts, scales better than ESD since Triest_fd samples edges within a given memory budget and discards the other edges. However, Triest_fd, which simply discards those unsampled edges, is significantly less accurate than our proposed algorithm ThinkD, which utilizes those unsampled edges to update estimates before discarding them. Although the idea of using unsampled edges has been considered for insertion-only streams [7, 14, 17, 19], applying the idea to fully dynamic graph streams has remained unexplored.

3 Notations and Problem Definition

Notations: Table 2 lists the symbols frequently used in the paper. Consider an undirected graph $\mathcal {G}=(\mathcal {V},\mathcal {E})$ with nodes $\mathcal {V}$ and edges $\mathcal {E}$. Each edge $\{u,v\}\in \mathcal {E}$ connects two distinct nodes $u\ne v\in \mathcal {V}$. We say a subset $\{u,v,w\}\subset \mathcal {V}$ of size 3 is a triangle if every pair of distinct nodes u, v, and w is connected by an edge in $\mathcal {E}$. We denote the set of global triangles (i.e., all triangles) in $\mathcal {G}$ by $\mathcal {T}$ and the set of local triangles of each node $u\in \mathcal {V}$ (i.e., all triangles containing u) by $\mathcal {T}[u]\subset \mathcal {T}$.

Assume the graph $\mathcal {G}$ evolves from the empty graph. We consider the fully dynamic graph stream representing the sequence of changes in $\mathcal {G}$, and denote the stream by $(e^{(1)},e^{(2)},...)$. For each $t\in \{1,2,...\}$, the pair $e^{(t)}=(\{u,v\},\delta )$ of an edge $\{u,v\}$ and a sign $\delta \in \{+,-\}$ denotes the change in $\mathcal {G}$ at time t. Specifically, $(\{u,v\},+)$ indicates the addition of a new edge $\{u,v\}\notin \mathcal {E}$, and $(\{u,v\},-)$ indicates the deletion of an existing edge $\{u,v\}\in \mathcal {E}$. We use $\mathcal {G}^{(t)}=(\mathcal {V}^{(t)},\mathcal {E}^{(t)})$ to indicate $\mathcal {G}$ at time t. That is,

$$\begin{aligned} \mathcal {E}^{(0)}=\emptyset \qquad \text {and} \qquad \mathcal {E}^{(t)}={\left\{ \begin{array}{ll} \mathcal {E}^{(t-1)}\cup \{\{u,v\}\}, &{} \text {if } e^{(t)}=(\{u,v\},+), \\ \mathcal {E}^{(t-1)}\setminus \{\{u,v\}\}, &{} \text {if } e^{(t)}=(\{u,v\},-). \end{array}\right. } \end{aligned}$$

Lastly, we let $\mathcal {T}^{(t)}$ denote the set of global triangles in $\mathcal {G}^{(t)}$ and $\mathcal {T}^{(t)}[u]\subset \mathcal {T}^{(t)}$ denote the set of local triangles of each node $u\in \mathcal {V}^{(t)}$ in $\mathcal {G}^{(t)}$.

Problem Definition (Problem 1): In this work, we address the problem of estimating the counts of global and local triangles in a fully dynamic graph stream. We assume the standard data stream model where the elements in the input stream, which may not fit in memory, can be accessed once in the given order unless they are explicitly stored in memory.

Problem 1

(Global and Local Triangle Counting in a Fully Dynamic Graph Stream).

• Given: a fully dynamic graph stream $(e^{(1)},e^{(2)},...)$

  (i.e., sequence of edge additions and deletions in graph $\mathcal {G}$)

• Maintain: estimates of global triangle count $|\mathcal {T}^{(t)}|$ and local triangle counts

  $\{(u,|\mathcal {T}^{(t)}[u]|)\}_{u\in \mathcal {V}^{(t)}}$ of graph $\mathcal {G}^{(t)}$ for current $t\in \{1,2,...\}$

• to Minimize: the estimation errors.

We follow a general approach of reducing the biases and variances of estimates simultaneously rather than minimizing a specific measure of estimation error.

4 Proposed Method: Think Before You Discard (ThinkD)

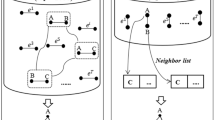
We propose ThinkD (Think before you Discard), which estimates the counts of global and local triangles in a fully dynamic graph stream. For estimation with limited memory, ThinkD samples edges and maintains those sampled edges, while discarding the other edges. The main idea of ThinkD is to fully utilize unsampled edges before they are discarded. Specifically, whenever each element in the input stream arrives, ThinkD first updates its estimates using the element. After that, if the element is an addition of an edge, ThinkD decides whether to sample the edge or not.

We present two versions of ThinkD and theoretically analyze their accuracies and complexities. To this end, we use $\bar{c}$ to denote the maintained estimate of the count of global triangles. Likewise, for each node u, we use c[u] to denote the maintained estimate of the count of local triangles of node u. In addition, we let $\mathcal {S}$ be the set of currently sampled edges, and for each node u, we let $\hat{\mathcal {N}}[u]$ be the set of neighbors of u in the graph composed of the edges in $\mathcal {S}$.

4.1 ThinkD$_{\text {fast}}$: Simple and Fast Version of ThinkD

ThinkD_fast, which is a simple and fast version of ThinkD, is described in Algorithm 1. ThinkD_fast initially has no sampled edges (line 1). Whenever each element $(\{u,v\},\delta )$ of the input stream arrives (line 2), ThinkD_fast first updates its estimates by calling the procedure Update (line 3). Then, if the element is an addition (i.e., $\delta =+$), ThinkD_fast samples the edge $\{u,v\}$ with a given sampling probability r (line 11) by calling the procedure Insert (line 4). If the element is a deletion (i.e., $\delta =-$), ThinkD_fast removes the edge $\{u,v\}$ from the existing samples (line 13) by calling the procedure Delete (line 5).

In the procedure Update, ThinkD_fast finds the triangles connected by the arrived edge $\{u,v\}$ and two edges from the existing samples $\mathcal {S}$ (line 7). To this end, ThinkD uses the fact that each common neighbor w of the nodes u and v in the graph composed of the sampled edges in $\mathcal {S}$ indicates the existence of such a triangle $\{u,v,w\}$. In the case of additions (i.e., $\delta =+$), since such triangles are new triangles added to the input stream, ThinkD_fast increases the estimates of the global count and the corresponding local counts (line 8). In the case of deletions (i.e., $\delta =-$), since such triangles are those removed from the input stream, ThinkD_fast decreases the estimates of the global count and the corresponding local counts (line 9). Notice that the amount of change per triangle is $1/r^{2}$, which is the reciprocal of the probability that each added or deleted triangle is discovered by ThinkD_fast. Note that each such triangle $\{u,v,w\}$ is discovered if and only if $\{w,u\}$ and $\{v,w\}$ are in $\mathcal {S}$, whose probability is $r^{2}$, as formalized in Lemma 1. This makes the expected amount of changes in the corresponding estimates for each such triangle be exactly one and thus makes ThinkD_fast give unbiased estimates, as explained in detail in Sect. 4.3.

Lemma 1

(Discovery Probability of Triangles in $\mathbf {ThinkD}_{\mathbf {fast}}$). In ThinkD_fast, any two distinct edges in graph $\mathcal {G}^{(t)}=(\mathcal {V}^{(t)},\mathcal {E}^{(t)})$ are sampled with probability $r^{2}$. That is, if we let $\mathcal {S}^{(t)}$ be $\mathcal {S}$ in Algorithm 1 after the t-th element $e^{(t)}$ is processed, then

$$\begin{aligned} Pr[\{u,v\}\in \mathcal {S}^{(t)}\cap \{w,x\}\in \mathcal {S}^{(t)}] = r^{2}, \ \forall t\ge 1,\ \forall \{u,v\}\ne \{w,x\}\in \mathcal {E}^{(t)}. \end{aligned}$$

(1)

Proof

Equation (1) holds since each edge is sampled independently with probability r. See Sect. A.1 of the supplementary document [1] for a formal proof.    $\blacksquare$

(Dis)advantages of $\mathbf {ThinkD}_{\mathbf {fast}}$: Due to its simplicity, ThinkD_fast is faster than its competitors, as shown empirically in Sect. 5.4. However, it is less accurate than ThinkD_acc, described in the following subsection, since it may discard edges even when memory is not full, leading to avoidable loss of information.

4.2 ThinkD$_{\text {acc}}$: Accurate Version of ThinkD

ThinkD_acc, which is an accurate version of ThinkD, is described in Algorithm 2. Unlike ThinkD_fast, which may discard edges even when memory is not full, ThinkD_acc maintains as many samples as possible within a given memory budget k (${\ge }2$) to minimize information loss.

To this end, ThinkD_acc uses a sampling method called Random Pairing (RP) [9]. Given a fully dynamic stream with deletions, and a memory budget k, RP maintains at most k samples while satisfying the uniformity of the samples. That is, if we let $\mathcal {E}$ be the set of edges remaining (without being deleted) in the input stream so far and $\mathcal {S}\subset \mathcal {E}$ be the set of samples being maintained by RP, then the following equations hold:

$$\begin{aligned} |\mathcal {S}|\le k \qquad \text {and} \qquad \ Pr[\mathcal {S}=\mathcal {A}]=Pr[\mathcal {S}=\mathcal {B}], \ \forall \mathcal {A}\ne \mathcal {B}\subset \mathcal {E}\text { s.t. } |\mathcal {A}|=|\mathcal {B}|. \end{aligned}$$

Updating the set $\mathcal {S}$ of samples using RP is described in lines 10–23. Whenever a deletion of an edge arrives, RP increases $n_{b}$ or $n_{g}$ depending on whether the edge is in $\mathcal {S}$ or not (lines 22 and 23). Roughly speaking, $n_{b}$ and $n_{g}$ denote the number of deletions that need to be “compensated” by additions (lines 16–18). If there is no deletion to compensate, RP processes each addition of an edge as in Reservoir Sampling [23]. That is, if memory is not full (i.e., $|\mathcal {S}|< k$), RP adds the new edge to $\mathcal {S}$ (line 13), while otherwise, RP replaces a random edge in $\mathcal {S}$ with the new edge with a certain probability (lines 14–15). We refer to [9] for the intuition behind the compensation and the details of RP; and we focus on how to use RP for triangle counting in the rest of this section.

Updating the estimates in ThinkD_acc is the same as that in ThinkD_fast except for the amount of change per triangle (lines 8 and 9), which is the reciprocal of the probability that each added or deleted triangle is discovered. When each element $e^{(t)}=(\{u,v\},\delta )$ arrives, each added or deleted triangle $\{u,v,w\}$ is discovered if and only if $\{w,u\}$ and $\{v,w\}$ are in $\mathcal {S}$. As shown in Lemma 2, if we let $y=\min (k,|\mathcal {E}|+n_{b}+n_{g})$, then the probability of such an event is

$$\begin{aligned} p(|\mathcal {E}|,n_{b},n_{g}) := \frac{y}{|\mathcal {E}|+n_{b}+n_{g}}\times \frac{y-1}{|\mathcal {E}|+n_{b}+n_{g}-1}. \end{aligned}$$

(2)

Lemma 2

(Discovery Probability of Triangles in $\mathbf {ThinkD}_{\mathbf {acc}}$). In ThinkD_acc, any two distinct edges in graph $\mathcal {G}^{(t)}=(\mathcal {V}^{(t)},\mathcal {E}^{(t)})$ are sampled with probability as in Eq. (2). That is, if we let $p^{(t)}$ and $\mathcal {S}^{(t)}$ be the values of Eq. (2) and $\mathcal {S}$, resp., in Algorithm 2 after the t-th element $e^{(t)}$ is processed, then

$$\begin{aligned} Pr[\{u,v\}\in \mathcal {S}^{(t)}\cap \{w,x\}\in \mathcal {S}^{(t)}] = p^{(t)}, \ \forall t\ge 1, \ \forall \{u,v\}\ne \{w,x\}\in \mathcal {E}^{(t)}. \end{aligned}$$

(3)

Proof

See Sect. A.2 of the supplementary document [1] for a proof.    $\blacksquare$

(Dis)advantages of $\mathbf {ThinkD}_{\mathbf {acc}}$ : Within the same memory budget, ThinkD_acc is slower than ThinkD_fast since ThinkD_acc maintains and processes more samples on average. However, ThinkD_acc is more accurate than ThinkD_fast by utilizing more samples. These are shown empirically in Sects. 5.3 and 5.4.

Reducing Estimation Errors by Sacrificing Unbiasedness: The estimates (i.e., $\bar{c}$ and c[u] for each node u) in Algorithms 1 and 2 can have negative values. Since true triangle counts are always non-negative, lower bounding the estimates by zero always reduces the estimation errors. However, the estimates become biased, and Theorem 1 in the following section does not hold anymore.

4.3 Accuracy Analyses

We prove that ThinkD_fast and ThinkD_acc maintain unbiased estimates with the expected values equal to the true global and local triangle counts. Then, we analyze the variances of the estimates that ThinkD_fast maintains. To this end, for each variable (e.g., $\bar{c}$) in Algorithms 1 and 2, we use superscript (t) (e.g., $\bar{c}^{(t)}$) to denote the value of the variable after the t-th element $e^{(t)}$ is processed.

We first define added triangles and deleted triangles in Definitions 1 and 2.

Definition 1

(Added Triangles). Let $\mathcal {A}^{(t)}$ be the set of triangles that have been added to graph $\mathcal {G}$ at time t or earlier. Formally,

$$ \mathcal {A}^{(t)}:= \{(\{u,v,w\},s):1\le s\le t \text { and } \{u,v,w\}\notin \mathcal {T}^{(s-1)}\text { and } \{u,v,w\}\in \mathcal {T}^{(s)}\}, $$

where addition time s is for distinguishing triangles composed of the same nodes but added at different times.¹

Definition 2

(Deleted Triangles). Let $\mathcal {D}^{(t)}$ be the set of triangles that have been removed from graph $\mathcal {G}$ at time t or earlier. Formally,

$$ \mathcal {D}^{(t)}:= \{(\{u,v,w\},s):1\le s\le t \text { and } \{u,v,w\}\in \mathcal {T}^{(s-1)}\text { and } \{u,v,w\}\notin \mathcal {T}^{(s)}\}, $$

where deletion time s is for distinguishing triangles composed of the same nodes but deleted at different times (see footnote 1).

Similarly, for each node $u\in \mathcal {V}^{(t)}$, we use $\mathcal {A}^{(t)}[u]\subset \mathcal {A}^{(t)}$ and $\mathcal {D}^{(t)}[u]\subset \mathcal {D}^{(t)}$ to denote the added and deleted triangles with node u, respectively. Lemma 3 formalizes the relationship between these concepts and the number of triangles.

Lemma 3

(Count of Triangles in the Current Graph). The count of triangles in the current graph equals to the count of added triangles subtracted by the count of deleted triangles. Formally,

$$\begin{aligned} |\mathcal {T}^{(t)}|&=|\mathcal {A}^{(t)}|-|\mathcal {D}^{(t)}|, \ \forall t\ge 1, \end{aligned}$$

(4)

$$\begin{aligned} |\mathcal {T}^{(t)}[u]|&=|\mathcal {A}^{(t)}[u]|-|\mathcal {D}^{(t)}[u]|, \ \forall t\ge 1, \ \forall u\in \mathcal {V}^{(t)}. \end{aligned}$$

(5)

Proof

Equations (4) and (5) follow from Definitions 1 and 2. See Sect. A.3 of the supplementary document [1] for a formal proof.    $\blacksquare$

Based on these concepts, we prove that ThinkD_fast and ThinkD_acc maintain unbiased estimates in Theorem 1. For the unbiasedness of the estimate $\bar{c}$ of the global count, we show that the expected amount of change in $\bar{c}$ for each added triangle is $+1$, while that for each deleted triangle is $-1$. Then, by Lemma 3, the expected value of $\bar{c}$ equals to the true global count. Likewise, we show the unbiasedness of the estimate of the local triangle count of each node by considering only the added and deleted triangles incident to the node.

Theorem 1

(‘Any Time’ Unbiasedness of ThinkD).ThinkD gives unbiased estimates at any time. Formally, in Algorithms 1 and 2,

$$\begin{aligned} \mathbb {E}[\bar{c}^{(t)}]&=|\mathcal {T}^{(t)}|, \ \forall t\ge 1, \end{aligned}$$

(6)

$$\begin{aligned} \mathbb {E}[c^{(t)}[u]]&=|\mathcal {T}^{(t)}[u]|, \ \forall t\ge 1, \ \forall u\in \mathcal {V}^{(t)}. \end{aligned}$$

(7)

Proof

Consider a triangle $(\{u,v,w\},s)\in \mathcal {A}^{(t)}$, and let $e^{(s)}=(\{u,v\},+)$ without loss of generality. The amount $\alpha _{uvw}^{(s)}$ of change in each of $\bar{c}$, c[u], c[v], and c[w] due to the discovery of $(\{u,v,w\},s)$ in line 8 of Algorithm 1 or Algorithm 2 is

$$\alpha _{uvw}^{(s)}= {\left\{ \begin{array}{ll} 1/r^{2} &{} if \{v,w\}\in \mathcal {S}^{(s-1)}\text { and } \{w,u\}\in \mathcal {S}^{(s-1)}\text { in Algorithm 1} \\ 1/p^{(s-1)}&{} if \{v,w\}\in \mathcal {S}^{(s-1)}\text { and } \{w,u\}\in \mathcal {S}^{(s-1)}\text { in Algorithm 2} \\ 0 &{} otherwise. \end{array}\right. } $$

Then, from Eqs. (1) and (3), the following equation holds:

$$\begin{aligned} \alpha _{uvw}^{(s)}= {\left\{ \begin{array}{ll} \frac{1}{Pr[\{v,w\}\in \mathcal {S}^{(s-1)}\cap \{w,u\}\in \mathcal {S}^{(s-1)}]} &{} if \{v,w\}\in \mathcal {S}^{(s-1)}\text { and } \{w,u\}\in \mathcal {S}^{(s-1)}\\ 0 &{} otherwise. \end{array}\right. } \end{aligned}$$

Hence,

$$\begin{aligned} \mathbb {E}[\alpha _{uvw}^{(s)}]=1. \end{aligned}$$

(8)

Consider a triangle $(\{u,v,w\},s)\in \mathcal {D}^{(t)}$, and let $e^{(s)}=(\{u,v\},-)$ without loss of generality. The amount $\beta _{uvw}^{(s)}$ of change in each of $\bar{c}$, c[u], c[v], and c[w] due to the discovery of $(\{u,v,w\},s)$ in line 9 of Algorithm 1 or Algorithm 2 is

$$\beta _{uvw}^{(s)}= {\left\{ \begin{array}{ll} - 1/r^{2} &{} if \{v,w\}\in \mathcal {S}^{(s-1)}\text { and } \{w,u\}\in \mathcal {S}^{(s-1)}\text { in Algorithm 1} \\ - 1/p^{(s-1)}&{} if \{v,w\}\in \mathcal {S}^{(s-1)}\text { and } \{w,u\}\in \mathcal {S}^{(s-1)}\text { in Algorithm 2} \\ 0 &{} otherwise. \end{array}\right. } $$

Then, from Eqs. (1) and (3), the following equation holds:

$$\begin{aligned} \beta _{uvw}^{(s)}= {\left\{ \begin{array}{ll} \frac{-1}{Pr[\{v,w\}\in \mathcal {S}^{(s-1)}\cap \{w,u\}\in \mathcal {S}^{(s-1)}]} &{} if \{v,w\}\in \mathcal {S}^{(s-1)}\text { and } \{w,u\}\in \mathcal {S}^{(s-1)}\\ 0 &{} otherwise. \end{array}\right. } \end{aligned}$$

Hence,

$$\begin{aligned} \mathbb {E}[\beta _{uvw}^{(s)}]=-1. \end{aligned}$$

(9)

By definition, the following holds:

$$\bar{c}^{(t)}= \sum _{(\{u,v,w\},s)\in \mathcal {A}^{(t)}}\alpha _{uvw}^{(s)}\ + \sum _{(\{u,v,w\},s)\in \mathcal {D}^{(t)}}\beta _{uvw}^{(s)}.$$

By linearity of expectation, Eqs. (8), (9), and Lemma 3, the following holds:

$$\begin{aligned} \mathbb {E}[\bar{c}^{(t)}]&= \sum _{(\{u,v,w\},s)\in \mathcal {A}^{(t)}}\mathbb {E}[\alpha _{uvw}^{(s)}] \ + \sum _{(\{u,v,w\},s)\in \mathcal {D}^{(t)}}\mathbb {E}[\beta _{uvw}^{(s)}] \\&= \sum _{(\{u,v,w\},s)\in \mathcal {A}^{(t)}}1 \ + \sum _{(\{u,v,w\},s)\in \mathcal {D}^{(t)}}(-1) = |\mathcal {A}^{(t)}|-|\mathcal {D}^{(t)}| = |\mathcal {T}^{(t)}|. \end{aligned}$$

Likewise, for each node $u\in \mathcal {V}^{(t)}$, the following holds:

$$c^{(t)}[u]= \sum _{(\{u,v,w\},s)\in \mathcal {A}^{(t)}[u]}\alpha _{uvw}^{(s)}\ + \sum _{(\{u,v,w\},s)\in \mathcal {D}^{(t)}[u]}\beta _{uvw}^{(s)}.$$

By linearity of expectation, Eqs. (8), (9), and Lemma 3, the following holds:

$$\begin{aligned}&\mathbb {E}[c^{(t)}[u]] = \sum _{(\{u,v,w\},s)\in \mathcal {A}^{(t)}[u]}\mathbb {E}[\alpha _{uvw}^{(s)}] \ + \sum _{(\{u,v,w\},s)\in \mathcal {D}^{(t)}[u]}\mathbb {E}[\beta _{uvw}^{(s)}] \\&= \sum _{(\{u,v,w\},s)\in \mathcal {A}^{(t)}[u]}1 \ + \sum _{(\{u,v,w\},s)\in \mathcal {D}^{(t)}[u]}(-1) = |\mathcal {A}^{(t)}[u]|-|\mathcal {D}^{(t)}[u]| = |\mathcal {T}^{(t)}[u]|. \end{aligned}$$

   $\blacksquare$

In Sect. B of the supplementary document [1], we prove the formulas for the variances of estimates given by ThinkD_fast. Theorem 2 is implied by them.

Theorem 2

(Variance of $\mathbf {ThinkD}_{\mathbf {fast}}{\mathbf {).}}$ Given an input graph stream, the variances of estimates maintained by ThinkD_fast with the sampling probability r is proportional to $1/r^2$. Formally, in Algorithm 1,

$$\begin{aligned} Var[\bar{c}^{(t)}] = O(1/r^{2}), \ \forall t\ge 1, \quad \text {and} \quad Var[c^{(t)}[u]] = O(1/r^{2}), \ \forall t\ge 1, \ \forall u\in \mathcal {V}^{(t)}. \end{aligned}$$

Proof

See Theorem 5 in Sect. B of the supplementary document [1].    $\blacksquare$

4.4 Complexity Analyses

We analyze the time and space complexities of ThinkD_fast and ThinkD_acc. In our analyses, we use $\mathcal {\bar{V}}^{(t)}:=\bigcup _{s=1}^{t}\mathcal {V}^{(s)}$ to denote the set of nodes that appear in the t-th or earlier elements in the input stream.

Space Complexity: To process the first t elements in the input graph stream, ThinkD_fast and ThinkD_acc maintain one estimate for the global triangle count and at most $|\mathcal {\bar{V}}^{(t)}|$ estimates for the local triangle counts. In addition, ThinkD_fast maintains $|\mathcal {E}^{(t)}|\cdot r$ edges on average, while ThinkD_acc maintains up to k edges. Thus, the average space complexities of ThinkD_fast and ThinkD_acc are $O(|\mathcal {E}^{(t)}|\cdot r+|\mathcal {\bar{V}}^{(t)}|)$ and $O(k+|\mathcal {\bar{V}}^{(t)}|)$, respectively. The complexities become $O(|\mathcal {E}^{(t)}|\cdot r)$ and O(k) when only the global triangle count needs to be estimated.

Time Complexity: We prove the average time complexity of ThinkD_fast in Theorem 3, which implies Corollary 1, and the worst-case time complexity of ThinkD_acc in Theorem 4. Corollary 1 and Theorem 4 state that, given a fixed memory budget k, ThinkD_fast and ThinkD_acc scale linearly with the number of elements in the input stream.

Theorem 3

(Time Complexity of $\mathbf {ThinkD}_{\mathbf {fast}}{\mathbf {).}}$ Algorithm 1 takes $O(t+t^2r)$ on average to process the first t elements in the input stream.

Table 3. Summary of the real-world and synthetic graph streams used in our experiments. B: billion, M: million, K: thousand.

Proof

In Algorithm 1, the most expensive step in processing each element $e^{(s)}=(\{u,v\},\delta )$ is to intersect $\hat{\mathcal {N}}[u]$ and $\hat{\mathcal {N}}[v]$ (line 7), which takes $O(1+\mathbb {E}[|\hat{\mathcal {N}}[u]|+|\hat{\mathcal {N}}[v]|])=O(1+\mathbb {E}[|\mathcal {S}|])=O(1+sr)$ on average. Hence, processing the first t elements takes $\sum _{s=1}^{t}O(1+sr)=O(t+t^2r)$ on average.    $\blacksquare$

Corollary 1

(Time Complexity of $\mathbf {ThinkD}_{\mathbf {fast}}$ with Fixed Memory k). If $r=O(k/t)$ for a constant k $({\ge }\,1)$, then Algorithm 1 takes O(tk) on average to process the first t elements in the input stream.

Theorem 4

(Time Complexity of $\mathbf {ThinkD}_{\mathbf {acc}}{\mathbf {).}}$ Algorithm 2 takes O(tk) to process the first t elements in the input stream.

Proof

In Algorithm 2, the most expensive step in processing each element $e^{(s)}=(\{u,v\},\delta )$ is to intersect $\hat{\mathcal {N}}[u]$ and $\hat{\mathcal {N}}[v]$ (line 7), which takes $O(1+|\hat{\mathcal {N}}[u]|+|\hat{\mathcal {N}}[v]|)=O(k)$. Thus, processing the first t elements takes O(tk).    $\blacksquare$

5 Experiments

In this section, we review our experiments for answering the following questions:

• Q1. Illustration of Theorems: Does ThinkD give unbiased estimates? Does ThinkD scale linearly with the size of the input stream?

• Q2. Accuracy: Is ThinkD more accurate than its best competitors?

• Q3. Speed: Is ThinkD faster than its best competitors?

• Q4. Effects of Deletions: Is ThinkD consistently accurate regardless of the ratio of deleted edges?

In addition, in Sect. D of the supplementary document [1], we describe how ThinkD can be used to detect the sudden emergence of dense subgraphs, and we experimentally show that it outperforms state-of-the-art competitors.

Fig. 1.

ThinkD is provably accurate and scalable. (a) ThinkD gives unbiased estimates with smaller variances than its best competitor. (b) ThinkD maintains more accurate estimates with smaller confidence intervals than its best competitor. (c–d) ThinkD scales linearly with the size of the input stream.

5.1 Experimental Settings

Machines: We used a machine with a 3.60 GHz CPU and 32 GB RAM unless otherwise stated.

Datasets: We created fully dynamic graph streams with deletions using the real-world graphs listed in Table 3 as follows: (a) create the additions of the edges in the input graph and shuffle them, (b) choose $\alpha \%$ of the edges and create the deletions of them, (c) locate each deletion in a random position after the corresponding addition. We set $\alpha$ to $20\%$ unless otherwise stated (see Sect. 5.5 for its effect on accuracy). The created streams were streamed from the disk.

Implementations: We implemented ThinkD_fast, ThinkD_acc, Triest_fd [7], Triest_impr [7], ESD [10], and Mascot [14] in Java 1.7. In all of them, sampled edges are stored in the adjacency list format, and as described in the last paragraph of Sect. 4.2, estimates are lower bounded by zero.

Evaluation Metrics: Let x and $\{(u,x[u])\}_{u\in \mathcal {V}}$ be the true counts of global triangles and local triangles at the end of the input stream. Let $\hat{x}$ and $\{(u,\hat{x}[u])\}_{u\in \mathcal {V}}$ be the corresponding estimates obtained by the evaluated algorithm. We used global error, defined as $\frac{|x-\hat{x}|}{1+x}$, and RMSE, defined as $\sqrt{\frac{1}{|\mathcal {V}|}\sum _{u\in \mathcal {V}}(x[u]-\hat{x}[u])^{2}}$, to evaluate the accuracy of global and local triangle counting, respectively.

5.2 Q1. Illustration of Theorems

ThinkD Gives Unbiased Estimates (Theorem 1). We compared 10, 000 estimates of the global triangle count obtained by ThinkD_fast, ThinkD_acc, and Triest_fd, whose parameters were set so that on average $10\%$ of the edges are stored at the end of each graph stream. Figure 1(a) shows the distributions of the estimates at the end of the Facebook dataset. The means of the estimates were close to the true triangle count, consistently with Theorem 1 (i.e., unbiasedness of ThinkD). Moreover, ThinkD_acc and ThinkD_fast gave estimates with smaller variances than Triest_fd. Figure 1(b) shows how the 95% confidence intervals change over time in the Facebook dataset. ThinkD_fast and ThinkD_acc maintained more accurate estimates with smaller confidence intervals than Triest_fd. Between ThinkD_fast and ThinkD_acc, ThinkD_acc was more accurate.

ThinkD Scales Linearly (Corollary 1 and Theorem 4). We measured the elapsed times taken by ThinkD_fast and ThinkD_acc to process all elements in graph streams with different numbers of elements. To measure their speeds independently of the speed of the input stream, we ignored time taken to wait for the arrival of elements. In both algorithms, we set k and r so that on average $10^7$ edges are stored at the end of each input stream. Figure 1(c) shows the results in the Random datasets, which were created by the Erdös-Rényi model. Both ThinkD_fast and ThinkD_acc scaled linearly with the number of elements, as expected in Corollary 1 and Theorem 4. Notice that the largest dataset is $\mathbf {800}$ GB with $\mathbf {100}$ billion elements. As seen in Fig. 1(d), ThinkD_fast and ThinkD_acc showed linear scalability also in a graph stream with realistic structure, which we created by sampling different numbers of elements from the Friendster dataset.

Fig. 2.

ThinkD is accurate. ThinkD gives the best trade-off between space and accuracy. In particular, ThinkD_acc is up to $\mathbf {4.3{\times }}$ more accurate than Triest_fd within the same memory budget. Error bars denote $\pm 1$ standard error. ESD is inapplicable to local triangle counting.

5.3 Q2. Accuracy (ThinkD Is More Accurate Than Its Competitors)

We compared the accuracies of four algorithms that support edge deletions. As we changed the ratio of stored edges at the end of each input stream from $5\%$ to $40\%$, we measured the accuracies of ThinkD_fast, ThinkD_acc, and Triest_fd. ESD always stores the entire input stream in memory, and we set its parameter to 1.0 to maximize its accuracy. Each evaluation metric was averaged over 100 trials in the Friendster and Orkut datasets and 1, 000 trials in the others.² As seen in Fig. 2, ThinkD_fast and ThinkD_acc consistently gave the best trade-off between space and accuracy. Specifically, within the same memory budget, ThinkD_acc was up to $\mathbf {4{\times }}$ and $\mathbf {4.3{\times }}$ more accurate than Triest_fd in terms of global error and RMSE, respectively. Between our algorithms, ThinkD_acc consistently outperformed ThinkD_fast. We observed the same trend in the other datasets (see Fig. 5 in the supplementary document [1]).

Fig. 3.

ThinkD is fast. ThinkD gives the best trade-off between speed and accuracy. In particular, ThinkD_fast is up to $\mathbf {2.2{\times }}$ faster than Triest_fd when they are similarly accurate. Error bars denote $\pm 1$ standard error. ESD is inapplicable to local triangle counting.

Fig. 4.

ThinkD is consistently accurate regardless of the ratio of deleted edges. Error bars denote $\pm 1$ standard error. Triest_impr and Mascot are inapplicable when there are deletions. ESD is inapplicable to local triangle counting.

5.4 Q3. Speed (ThinkD Is Faster Than Its Competitors)

We compared the speeds and accuracies of four algorithms that support edge deletions. The detailed settings were the same as those in Sect. 5.3 except that we measured the performance of ESD as we changed its parameter from 0.2 to 1.0. To measure the speeds of the algorithms independently of the speed of the input stream, we ignored time taken to wait for the arrival of elements. As seen in Fig. 3, ThinkD_fast and ThinkD_acc consistently gave the best trade-off between speed and accuracy. Specifically, for the same global error and RMSE, ThinkD_fast was up to $\mathbf {2.2{\times }}$ faster than Triest_fd. Between our algorithms, ThinkD_fast consistently outperformed ThinkD_acc. We observed the same trend in the other datasets (see Fig. 6 in the supplementary document [1]).

5.5 Q4. Effects of Deletions (ThinkD Is Consistently Accurate)

We measured how the ratio of deleted edges (i.e., $\alpha$ in Sect. 5.1) in input graph streams affects the accuracies of the considered algorithms. In every algorithm, we set the ratio of stored edges at the end of each input stream to $10\%$. As seen in Fig. 4, all algorithms that support edge deletions became more accurate as input graphs became smaller with more deletions. ThinkD_fast and ThinkD_acc were similarly accurate with Mascot and Triest_impr, respectively, in the streams without deletions. In the streams with deletions, which Mascot and Triest_impr cannot handle, ThinkD_fast and ThinkD_acc were $\mathbf {1.8-3.4{\times }}$ more accurate than Triest_fd regardless of the ratio of deleted edges. We observed the same trend in the other datasets (see Fig. 7 in the supplementary document [1]).

6 Conclusion

We propose ThinkD, which estimates the counts of global and local triangles in a fully dynamic graph stream with edge additions and deletions. Our theoretical and empirical analyses show that ThinkD has the following advantages:

• Accurate: ThinkD is up to 4.3${\times }$ more accurate than its best competitors within the same memory budget (Fig. 2).

• Fast: ThinkD is up to 2.2${\times }$ faster than its best competitors with similar accuracies (Fig. 3). ThinkD processes terabyte-scale graph streams with linear scalability (Fig. 1, Corollary 1, and Theorem 4).

• Theoretically Sound: ThinkD maintains unbiased estimates (Theorem 1) with small variances (Theorem 2) at any time while the input graph evolves.

Reproducibility: The source code and datasets used in the paper are available at http://www.cs.cmu.edu/~kijungs/codes/thinkd/.