Abstract
In this paper we investigate extensions of Local Binary Patterns (LBP), Improved Local Binary Patterns (ILBP) and Extended Local Binary Patterns (ELBP) to colour textures via two different strategies: intra-/inter-channel features and colour orderings. We experimentally evaluate the proposed methods over 15 datasets of general and biomedical colour textures. Intra- and inter-channel features from the RGB space emerged as the best descriptors and we found that the best accuracy was achieved by combining multi-resolution intra-channel features with single-resolution inter-channel features.
R. Bello-Cerezo—Performed part of this work as a visiting graduate student in the Systems Design Engineering department at the University of Waterloo, Canada.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Colour and texture, along with transparency and gloss, are among the most important visual features of objects, materials and scenes. As a consequence, colour and texture analysis plays a fundamental role in many computer vision applications such as surface inspection [1,2,3], medical image analysis [4,5,6,7] and object recognition [8,9,10]. It is generally believed that combining colour and texture improves accuracy (at least under steady imaging conditions [11, 12]), though it is not quite clear which is the best way to do it. Indeed this has been subject of debate since early on, both in computer vision [11, 12] and perception science [13].
Approaches to colour texture analysis can be roughly categorised into three groups: parallel, sequential and integrative [14], though more involved taxonomies have been proposed too [15]. In this paper we investigate the problem of representing colour texture features starting from three LBP variants as grey-scale texture descriptors. Even in the era of Deep Learning, there are good reasons why Local Binary Patterns and related variations are worth investigating: they are conceptually simple, compact, easy to implement, computationally cheap – yet very accurate. We consider two strategies to extend LBP variants to colour textures: the combination of inter- and intra-channel features, and colour orderings. We also evaluate the effect of the colour space used (RGB, HSV, YUV and YIQ) and of the spatial resolution(s) of the local neighbourhood.
2 Background: Grey-Scale LBP Variants
Local Binary Patterns variants [16,17,18,19,20,21,22] (also referred to as Histograms of Equivalent Patterns [23]) are a well-known class of grey-scale texture descriptors. They are particularly appreciated for their conceptual ease, low computational demand yet high discrimination capability. Nonetheless, extensions to colour images have received much less attention than the original, grey-scale descriptors. In this paper we investigate extensions to the colour domain of Local Binary Patterns [16], Improved Local Binary Patterns [24] and Extended Local Binary Patterns [25], though the same methods could be easily extended to other descriptors of the same class (see [22] for an up-to-date review).
The three methods are all based on comparing the grey-levels of the pixels in a neighbourhood of given shape and size, but the comparison scheme is different in the three cases (see [16, 24, 25] for details). In general, any such comparison scheme can be regarded as a hand-designed function (also referred to as the kernel function [23]), which maps a local image pattern to one visual word among a set of pre-defined ones (dictionary). In formulas, denoted with \(\mathcal {N}\) the neighbourhood, \(\mathcal {P}\) a local image pattern (set of grey-scale values over that neighbourhood) and f the kernel function we can write:
where \(\{w_1,\dots ,w_K\}\) is the dictionary. Consequently, any LBP variant identifies with its kernel function and vice-versa, as clearly shown in [26]. The dimension of the dictionary depends on the kernel function and the number of pixels in the neighbourhood: standard LBP [16, 18, 19] for instance generates a dictionary of \(2^{n-1}\) words, being n the number of pixels in the neighbourhood. Image features are the one-dimensional, orderless distribution of the visual words over the dictionary (bag of visual words model).
Rotation-invariant versions of LBP and variants are computed by grouping together the visual words that can be obtained from one another via a discrete rotation of the peripheral pixels (also usually referred to as the ‘ri’ configuration [16]). In this case the dimension of the (reduced) dictionary can be computed through standard combinatorial methods [27].
3 Extensions to Colour Images
3.1 Intra- and Inter-channel Analysis
Intra- and/or inter-channel analysis are classic tools for extending texture descriptors to colour images [28,29,30]. Intra-channel features are computed from each colour channel separately, inter-channel features from pairs of channels. In both cases the resulting features are concatenated into a single vector. As for inter-channel features, if we consider three-channel images and indicate with i, j and k the colour channels, there are six possible combinations: ij, ik, jk, ji, ki and kj. However, to avoid redundancy and reduce the overall number of features, it is customary to retain only the first three [29, 30]. Figures 1 and 2 show how to compute intra- and inter-channel features in the RGB space.
Intra- and inter-channel analysis applies to grey-scale LBP variants by replacing the comparison between the grey levels with that between the intensity levels within each colour channel and/or pairs of them, respectively. Therefore, both intra- and inter-channel analysis multiply by three the dimension of the original descriptor (by six when used together). Intra- and inter-channel analysis extends LBP, ILBP and ELBP seamlessly to the colour domain. In the remainder we refer to these colour extensions respectively as Opponent Colour LBP (OCLBP) [29], Improved Opponent Colour LBP (IOCLBP) [30] and Extended Opponent Colour LBP (EOCLBP).
3.2 Colour Orderings
Differently from grey-scale, colour data are multivariate, hence lack a natural ordering. Still, higher-dimension analogues of univariate orderings can be introduced by recurring to some sub- (i.e. less than total) ordering principles [31]. Herein we considered the following three types of sub-orderings in the colour space: lexicographic order, order based on the colour vector norm and order based on a reference colour [32,33,34,35,36,37]. The first is a marginal ordering (M-ordering), the second and third are reduced (or aggregate) orderings (R-orderings) [31]. In the remainder we use subscripts ‘lex’, ‘cvn’ and ‘rcl’ to indicate the three orderings. Once the order is defined, the grey-scale descriptors introduced in Sect. 2 extend seamlessly to the colour domain. Also note that colour orderings produce more compact descriptors than intra- and inter-channel analysis, for the number of features is, in this case, the same as that of the original grey-scale descriptor.
Lexicographic Order. The lexicographic order [32, 34] involves defining some kind of (arbitrary) priority among the colour channels. Denoted with i, j and k the three channels, one can for instance establish that i has higher priority than j and j higher than k. In that case, given two colours \(\mathbf {C}_1 = \{C_{1i},C_{1j},C_{1k}\}\) and \(\mathbf {C}_2 = \{C_{2i},C_{2j},C_{2k}\}\), we shall write:
For three-dimensional colour data there are \(3! = 6\) priority rules, and, consequently, as many lexicographic orders.
Aggregate Order Based on the Colour Vector Norm. This is based on comparing the vector norm [33] of the two colours:
where ‘\(||\cdot ||\)’ indicates the vector norm. In the remainder we shall assume that this be the \(L_2\) norm, although other types of distance can be used as well.
Aggregate Order Based on a Reference Colour. In this case the comparison is based on the distance from a given (and again arbitrary) reference colour \(\mathbf {C}_\text {ref}\) [35]:
Clearly this case reduces to the order based on the colour vector norm when \(\mathbf {C}_\text {ref} = \{0,0,0\}\).
4 Experiments
Different strategies have been proposed to extend LBP (and variants) to colour textures. In order to evaluate the effectiveness of the approaches described in Sect. 3 and to explore which one works better in the case of colour images, we carried out a set of supervised image classification experiments using 15 colour texture datasets (more details on this in Sect. 5). We first run a group of three experiments to determine the optimal settings regarding the colour space used (Experiment 1), the colour orderings (Experiment 2) and the combination of resolutions for intra- and inter-channel features (Experiment 3). To reduce the overall computational burden we only used datasets #1 to #5 for this first group of experiments. Finally, in the last experiment we selected the best settings and carried out a comprehensive evaluation using all the datasets.
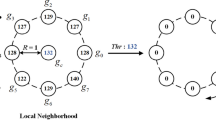
We computed rotation-invariant (‘ri’) features from non-interpolated pixel neighbourhoods of radius 1px, 2px and 3px (Fig. 3) and concatenated them. In the remainder, symbol ‘&’ will indicate concatenation; therefore we shall write, for instance, ‘1&2&3’ to signal concatenation of the feature vectors computed at resolution 1, 2 and 3.
The accuracy was estimated via split sample validation with stratified sampling using a train ratio of 1/2, i.e.: half of the samples of each class (train set) were used to train the classifier and the remaining half (test set) to compute the figure of merit. This was the fraction of samples of the test set classified correctly. Classification was based on the nearest neighbour rule with \(L_1\) (‘cityblock’) distance.
4.1 Experiment 1: Selecting the Best Colour Space for Intra- and Inter-channel Features
This experiment aimed to determine the best colour space among RGB, HSV, YUV and YIQ (conversion formulae from RGB available in [38]). Since HSV separates colour into heterogeneous components (hue, saturation and value), we also used a normalized version of this space (HSV\(_\text {norm}\) in the remainder):
where \(\mu \) and \(\sigma \) indicate the average values over the input image. Normalized versions of YUV and YIQ were also considered, but not reported in the results owing to their poor performance. We computed both intra- and inter-channel features at resolutions 1, 2 and 3, and concatenated the results (‘1&2&3’). We considered the following combinations of colour spaces respectively for the intra- and inter-channel features: RGB-RGB, HSV-HSV, HSV-RGB, HSV-HSV\(_\text {norm}\), HSV-YUV and HSV-YIQ (see Table 3, boldface figures).
4.2 Experiment 2: Colour Orderings Vs. Intra- and Inter-channel Features
The objective of this experiment was to evaluate the effectiveness of intra- and inter-channel features compared with colour orderings (Sect. 3.2) in the RGB colour space, which emerged as the best one from Experiment 1. For the lexicographic order we considered all the six possible combinations of priority among the R, G and B channels, though for the sake of simplicity we only report (see Table 4) the results of the combination that attained the best accuracy in the majority of the cases (this was \(G \succ R \succ B\)). For the order based on a reference colour we considered three possible references, the same three used in [36] since they were the best among the eight vertices of the RGB colour cube: white (1,1,1), green (0,1,0) and magenta (1,0,1), and the first gave the best results (see Table 4). As in Experiment 1, the image features were computed at resolution 1, 2 and 3 and the resulting vectors concatenated (‘1&2&3’).
4.3 Experiment 3: Selecting Optimal Resolutions for Intra- and Inter-channel Features
Since the use of intra- and inter-channel analysis increased by six the number of features of grey-scale descriptors, in this experiment we investigated how to reduce the overall number of features – this way generating reasonably compact descriptors – by selecting appropriate resolutions for intra- and inter-channel features. Specifically, we used three concatenated resolutions (‘1&2&3’) for intra-channel features and one (‘1’, ‘2’ or ‘3’) or two concatenated resolutions (‘1&2’, ‘1&3’ or ‘2&3’) for inter-channel features.
4.4 Experiment 4: Overall Evaluation with Optimised Settings
In this last experiment we computed the classification accuracy over all the 15 datasets described in Sect. 5 using the settings that emerged as optimal from the previous experiments. For calibration purposes we also included five pre-trained convolutional neural network models – specifically: three residual networks (ResNet-50, ResNet-101 and ResNet-152 [39]) and two VGG ‘very deep’ models (VGG-VeryDeep-16 and VGG-VeryDeep-19 [40]). Image features in this case were the \(L_1\) normalised output of the last fully-connected layer (usually referred to as the ‘FC’ configuration [41, 42]). The results are reported in Tables 6–7.
Table 3 summarises the results of Experiment 1. As can be seen, the RGB-RGB combination for intra- and inter-channel features emerged as the best option in seven datasets, followed by HSV-HSV (five datasets) and HSV-RGB (four datasets).
5 Datasets
For the experimental evaluation we considered eight datasets of generic colour textures and seven of biomedical textures as detailed in Sects. 5.1–5.2. The main characteristics of each dataset are also summarised in Tables 1–2.
5.1 Generic Colour Textures
#1 – #2: KTH-TIPS [43, 44] and KTH-TIPS2b [44, 45]. Generic materials as bread, cotton, cracker, linen, orange peel, sandpaper, sponge or styrofoam, acquired at nine scales, three viewpoints and three different illuminants.
#3 – #4: Outex-00013 [16, 46] and Outex-00014 [16, 46]. Generic materials such as carpet, chips, flakes, granite, paper, pasta or wallpaper. Images from Outex-00013 were acquired under invariable imaging conditions and those from Outex-00014 under three different illumination conditions.
#5, #7 – #8: PlantLeaves [47], ForestSpecies [48, 49] and NewBarkTex [50, 51]. Images from different species of plants, trees and bark acquired under controlled and steady imaging conditions.
#6: CUReT [52]. A reduced version of the Columbia-Utrecht Reflectance and Texture database maintained by the Visual Geometry Group, University of Oxford, United Kingdom [53], containing samples of generic materials.
5.2 Biomedical Textures
The following databases were acquired through digital microscopy under fixed and reproducible conditions, and are therefore intrinsically different from those presented in the preceding section.
#9: BioMediTechRPE [54, 55]. Retinal pigment epithelium (RPE) cells from different stages of maturation.
#10 – #13: BreakHis [56, 57]. Histological images from benign/malignant breast cancer tissue. Each image was taken under four magnification factors (40\(\times \), 100\(\times \), 200\(\times \) and 400\(\times \)), and we considered each factor as making up a different dataset (see Table 2).
#14 – #15: Epistroma [5, 58] and Kather [59,60,61]. Histological images from colorectal cancer tissue representing different tissue sub-types.
6 Results and Discussion
The results of Experiment 2 (Table 4) show that in most cases intra- and inter-channel features from the RGB space improved the accuracy of the original, grey-scale descriptors by a good margin. By contrast, no clear advantage emerged from using colour orderings as an alternative to grey-scale values.
Experiment 3 indicated that the best accuracy was achieved by concatenating multi-resolution intra-channel features and single-resolution inter-channel features. In fact, adding more than one inter-channel resolution degraded the performance in the majority of cases, as clearly shown in Table 5. The results were however inconclusive as to which resolution (‘1’, ‘2’ or ‘3’) should be used.
The comparison between LBP variants and pre-trained convolutional networks (Experiment 4, Tables 6 and 7) showed nearly perfectly split results, with the former achieving the best performance in seven datasets out of 15 and the reverse occurring in the other eight. Convolutional models seemed better at classifying textures with higher intra-class variability (as a consequence of texture non-stationariness and/or changes in the imaging conditions), as for instance in datasets #1, #2 and #7 (see Sect. 5.1). Conversely, homogeneous textures acquired under steady imaging conditions (most of the biomedical datasets) were still better classified by LBP variants. This finding generally agrees with those obtained in previous studies [62]. Pre-trained convolutional networks, however, achieved this result by employing at least twice as many features than LBP variants.
7 Conclusions
In this work we have investigated two strategies for extending LBP variants to the colour domain: intra- and inter-channel features on the one hand and colour orderings on the other. Colour orderings did not prove particularly effective; however, intra- and inter-channel features improved the accuracy of the original, grey-scale descriptors in virtually all the cases. The best results were obtained by combining multi-resolution intra-channel features with single-resolution inter-channel features, and this represents a novel finding. In future works we plan expand the study to consider more LBP variants [22] and different strategies for compacting the feature vectors [63].
References
Weszka, J.S., Rosenfeld, A.: An application of texture analysis to materials inspection. Pattern Recognit. 8(4), 195–200 (1976)
Tsai, D.M., Huang, T.Y.: Automated surface inspection for statistical textures. Image Vis. Comput. 21(4), 307–323 (2003)
Koch, C., Georgieva, K., Kasireddy, V., Akinci, B., Fieguth, P.: A review on computer vision based defect detection and condition assessment of concrete and asphalt civil infrastructure. Adv. Eng. Inform. 29(2), 196–210 (2015)
Meijer, G.A., Beliën, J.A.M., Van Diest, P.J., Baak, J.P.A.: Image analysis in clinical pathology. J. Clin. Pathol. 50(5), 365–370 (1997)
Linder, N., et al.: Identification of tumor epithelium and stroma in tissue microarrays using texture analysis. Diagn. Pathol. 7(22), 1–11 (2012)
Nanni, L., Lumini, A., Brahnam, S.: Local binary patterns variants as texture descriptors for medical image analysis. Artif. Intell. Med. 49(2), 117–125 (2010)
Jalalian, A., Mashohor, S., Mahmud, R., Karasfi, B., Saripan, I., Ramli, A.R.: Computer-assisted diagnosis system for breast cancer in computed tomography laser mammography (CTLM). J. Digit. Imaging 30(6), 796–811 (2017)
Lowe, D.G.: Object recognition from local scale-invariant features. In: Proceedings of Seventh IEEE International Conference on Computer Vision, 1999, vol. 2, pp. 1150–1157 (1999)
Serre, T., Wolf, L., Bileschi, S., Riesenhuber, M., Poggio, T.: Robust object recognition with cortex-like mechanisms. IEEE Trans. Pattern Anal. Mach. Intell. 29(3), 411–426 (2007)
Liu, H., Wu, Y., Sun, F., Guo, D.: Recent progress on tactile object recognition. Int. J. Adv. Robot. Syst. 14(4) (2017)
Drimbarean, A., Whelan, P.: Experiments in colour texture analysis. Pattern Recognit. Lett. 22(10), 1161–1167 (2001)
Mäenpää, T., Pietikäinen, M.: Classification with color and texture: jointly or separately? Pattern Recognit. Lett. 37(8), 1629–1640 (2004)
Cavina-Pratesi, C., Kentridge, R.W., Heywood, C., Milner, A.: Separate channels for processing form, texture, and color: evidence from FMRI adaptation and visual object agnosia. Cereb. Cortex 20(10), 2319–32 (2010)
Palm, C.: Color texture classification by integrative co-occurrence matrices. Pattern Recognit. 37(5), 965–976 (2004)
Bianconi, F., Harvey, R., Southam, P., Fernández, A.: Theoretical and experimental comparison of different approaches for color texture classification. J. Electron. Imaging 20(4) (2011). Article number 043006
Ojala, T., Pietikäinen, M., Mäenpää, T.: Multiresolution gray-scale and rotation invariant texture classification with local binary patterns. IEEE Trans. Pattern Anal. Mach. Intell. 24(7), 971–987 (2002)
Huang, D., Shan, C., Ardabilian, M., Wang, Y., Chen, L.: Local binary patterns and its application to facial image analysis: a survey. IEEE Trans. Syst. Man Cybern. Part C 41(6), 765–781 (2017)
Pietikäinen, M., Hadid, A., Zhao, G., Ahonen, T.: Computer Vision Using Local Binary Patterns. Computational Imaging and Vision, vol. 40. Springer, Heidelberg (2011). https://doi.org/10.1007/978-0-85729-748-8
Brahnam, S., Jain, L., Nanni, L., Lumini, A.: Local Binary Patterns: New Variants and Applications. Studies in Computational Intelligence, vol. 506. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-39289-4
Pietikäinen, M., Zhao, G.: Two decades of local binary patterns: a survey. In: Bingham, E., Kaski, S., Laaksonen, J., Lampinen, J. (eds.) Advances in Independent Component Analysis and Learning Machines, pp. 175–210. Academic Press, London (2015)
Liu, L., Lao, S., Fieguth, P., Guo, Y., Wang, X., Pietikäinen, M.: Median robust extended local binary pattern for texture classification. IEEE Trans. Image Process. 25(3), 1368–1381 (2016)
Liu, L., Fieguth, P., Guo, Y., Wang, X., Pietikäinen, M.: Local binary features for texture classification: taxonomy and experimental study. Pattern Recognit. 62, 135–160 (2017)
Fernández, A., Álvarez, M.X., Bianconi, F.: Texture description through histograms of equivalent patterns. J. Math. Imaging Vis. 45(1), 76–102 (2013)
Jin, H., Liu, Q., Lu, H., Tong, X.: Face detection using improved LBP under Bayesian framework. In: Proceedings of the 3rd International Conference on Image and Graphics, Hong Kong, China, pp. 306–309, December 2004
Liu, L., Zhao, L., Long, Y., Kuang, G., Fieguth, P.: Extended local binary patterns for texture classification. Image Vis. Comput. 30(2), 86–99 (2012)
Bianconi, F., Fernández, A.: A unifying framework for LBP and related methods. In: Brahnam, S., Jain, L.C., Nanni, L., Lumini, A. (eds.) Local Binary Patterns: New Variants and Applications. Studies in Computational Intelligence, vol. 506, pp. 17–46. Springer, Heidelberg (2014). https://doi.org/10.1007/978-3-642-39289-4_2
Charalambides, C.A.: Enumerative Combinatorics. Discrete Mathematics and Its Applications. Chapman and Hall/CRC, Boca Raton (2002)
Jain, A., Healey, G.: A multiscale representation including opponent color features for texture recognition. IEEE Trans. Image Process. 7(1), 124–128 (1998)
Mäenpää, T., Pietikäinen, M.: Texture analysis with local binary patterns. In: Chen, C.H., Wang, P.S.P. (eds.) Handbook of Pattern Recognition and Computer Vision, 3rd edn, pp. 197–216. World Scientific Publishing, London (2005)
Bianconi, F., Bello-Cerezo, R., Napoletano, P.: Improved opponent colour local binary patterns: an effective local image descriptor for colour texture classification. J. Electron. Imaging 27(1) (2017)
Barnett, V.: The ordering of multivariate data. J. R. Stat. Soc. Ser. A (Gen.) 139(3), 318–355 (1976)
Aptoula, E., Lefèvre, S.: A comparative study ion multivariate mathematical morphology. Pattern Recognit. 40(11), 2914–2929 (2007)
Porebski, A., Vandenbroucke, N., Macaire, L.: Haralick feature extraction from LBP images for colour texture classification. In: Proceedings of the International Workshops on Image Processing Theory, Tools and Applications (IPTA 2008), Sousse, Tunisie, pp. 1–8 (2008)
Barra, V.: Expanding the local binary pattern to multispectral images using total orderings. In: Richard, P., Braz, J. (eds.) VISIGRAPP 2010. CCIS, vol. 229, pp. 67–80. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-25382-9_5
Ledoux, A., Richard, N., Capelle-Laizé, A.-S., Fernandez-Maloigne, C.: Toward a complete inclusion of the vector information in morphological computation of texture features for color images. In: Elmoataz, A., Lezoray, O., Nouboud, F., Mammass, D. (eds.) ICISP 2014. LNCS, vol. 8509, pp. 222–229. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-07998-1_25
Ledoux, A., Losson, O., Macaire, L.: Color local binary patterns: compact descriptors for texture classification. J. Electron. Imaging 25(6) (2016)
Fernández, A., Lima, D., Bianconi, F., Smeraldi, F.: Compact colour texture descriptor based on rank transform and product ordering in the RGB color space. In: Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops (ICCVW) (2017)
Palus, H.: Representations of colour images in different colour spaces. In: Sangwine, S.J., Horne, R.E.N. (eds.) The Colour Image Processing Handbook, pp. 67–90. Springer, Boston (1998). https://doi.org/10.1007/978-1-4615-5779-1_4
He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. In: 2016 IEEE Conference on Computer Vision and Pattern Recognition (2016)
Simonyan, K., Zisserman, A.: Very deep convolutional networks for large-scale image recognition. In: Proceedings of the 5th International Conference on Learning Representations, San Diego, USA, May 2015
Cimpoi, M., Maji, S., Kokkinos, I., Vedaldi, A.: Deep filter banks for texture recognition, description, and segmentation. Int. J. Comput. Vis. 118(1), 65–94 (2016)
Cusano, C., Napoletano, P., Schettini, R.: Evaluating color texture descriptors under large variations of controlled lighting conditions. J. Opt. Soc. Am. A 33(1), 17–30 (2016)
Hayman, E., Caputo, B., Fritz, M., Eklundh, J.-O.: On the significance of real-world conditions for material classification. In: Pajdla, T., Matas, J. (eds.) ECCV 2004. LNCS, vol. 3024, pp. 253–266. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24673-2_21
The kth-tips and kth-tips2 image databases. http://www.nada.kth.se/cvap/databases/kth-tips/download.html. Accessed 11 Jan 2017
Caputo, B., Hayman, E., Mallikarjuna, P.: Class-specific material categorisation. In: Proceedings of the Tenth IEEE International Conference on Computer Vision (ICCV 2005), vol. 2, pp. 1597–1604 (2005)
Outex texture database. http://www.outex.oulu.fi/. Accessed 12 Jan 2017
Casanova, D., Sá, J.J., Bruno, O.: Plant leaf identification using Gabor wavelets. Int. J. Imaging Syst. Technol. 19(3), 236–246 (2009)
Forest species database. http://web.inf.ufpr.br/vri/image-and-videos-databases/forest-species-database. Accessed 11 Jan 2017
Martins, J., Oliveira, L.S., Nigkoski, S., Sabourin, R.: A database for automatic classification of forest species. Mach. Vis. Appl. 24(3), 567–578 (2013)
New BarkTex benchmark image test suite for evaluating color texture classification schemes. https://www-lisic.univ-littoral.fr/~porebski/BarkTex_image_test_suite.html. Accessed 12 Jan 2017
Porebski, A., Vandenbroucke, N., Macaire, L., Hamad, D.: A new benchmark image test suite for evaluating color texture classification schemes. Multimed. Tools Appl. J. 70(1), 543–556 (2014)
CUReT: columbia-utrecht reflectance and texture database. http://www.cs.columbia.edu/CAVE/software/curet/index.php. Accessed 25 Jan 2017
Visual geometry group: CUReT: columbia-utrecht reflectance and texture database. http://www.robots.ox.ac.uk/~vgg/research/texclass/setup.html. Accessed 26 Jan 2017
BioMediTechRPE database (2016). https://figshare.com/articles/BioMediTech_RPE_dataset/2070109. Accessed 16 May 2017
Nanni, L., Paci, M., Santos, F.L.C., Skottman, H., Juuti-Uusitalo, K., Hyttinen, J.: Texture descriptors ensembles enable image-based classification of maturation of human stem cell-derived retinal pigmented epithelium. Plos One 11(2) (2016)
Breast cancer histopathological database (breakhis) (2015). http://web.inf.ufpr.br/vri/breast-cancer-database. Accessed 16 May 2017
Spanhol, F., Oliveira, L.S., Petitjean, C., Heutte, L.: Breast cancer histopathological image classification using convolutional neural networks. In: International Joint Conference on Neural Networks (IJCNN 2016), Vancouver, Canada (2016)
Webmicroscope. EGFR colon TMA stroma LBP classification (2012). http://fimm.webmicroscope.net/Research/Supplements/epistroma. Accessed 16 May 2017
Collection of texture in colorectal cancer histology (2016). https://zenodo.org/record/53169#.WRsdEPmGN0w. Accessed 16 May 2017
Kather, J.N., Marx, A., Reyes-Aldasoro, C.C., Schad, L.R., Zöllner, F.G., Weis, C.A.: Continuous representation of tumor microvessel density and detection of angiogenic hotspots in histological whole-side images. Oncotarget 6(22), 19163–19176 (2015)
Kather, J.N., et al.: Multi-class texture analysis in colorectal cancer histology. Sci. Rep. 6 (2016). 27988
Bello-Cerezo, R., Bianconi, F., Cascianelli, S., Fravolini, M.L., di Maria, F., Smeraldi, F.: Hand-designed local image descriptors vs. off-the-shelf CNN-based features for texture classification: an experimental comparison. In: De Pietro, G., Gallo, L., Howlett, R.J., Jain, L.C. (eds.) KES-IIMSS 2017. SIST, vol. 76, pp. 1–10. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-59480-4_1
Orjuela, S., Quinones, R., Ortiz-Jaramillo, B., Rooms, F., De Keyser, R., Philips, W.: Improving textures discrimination in the local binary patterns technique by using symmetry & group theory. In: Proceedings of the 17th International Conference on Digital Signal Processing, Corfu, Greece, July 2011. Article no. 6004978
Acknowledgments
R. Bello-Cerezo wants to thank the colleagues at Systems Design Engineering, University of Waterloo, Canada, for the assistance received during her research visit from Sep. 2017 to Feb. 2018. F. Bianconi wishes to acknowledge support from the Italian Ministry of University and Research (MIUR) under the Individual Funding Scheme for Fundamental Research (‘FFABR’ 2017) and from the Department of Engineering at the Università degli Studi di Perugia, Italy, under the Fundamental Research Grants Scheme 2018.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Bello-Cerezo, R., Fieguth, P., Bianconi, F. (2019). LBP-Motivated Colour Texture Classification. In: Leal-Taixé, L., Roth, S. (eds) Computer Vision – ECCV 2018 Workshops. ECCV 2018. Lecture Notes in Computer Science(), vol 11132. Springer, Cham. https://doi.org/10.1007/978-3-030-11018-5_42
Download citation
DOI: https://doi.org/10.1007/978-3-030-11018-5_42
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-11017-8
Online ISBN: 978-3-030-11018-5
eBook Packages: Computer ScienceComputer Science (R0)