Multiple Wavelet Pooling for CNNs

Abstract

Pooling layers are an essential part of any Convolutional Neural Network. The most popular pooling methods, as max pooling or average pooling, are based on a neighborhood approach that can be too simple and easily introduce visual distortion. To tackle these problems, recently a pooling method based on Haar wavelet transform was proposed. Following the same line of research, in this work, we explore the use of more sophisticated wavelet transforms (Coiflet, Daubechies) to perform the pooling. Additionally, considering that wavelets work similarly to filters, we propose a new pooling method for Convolutional Neural Network that combines multiple wavelet transforms. The results achieved demonstrate the benefits of our approach, improving the performance on different public object recognition datasets.

1 Introduction

Neural networks, the main tool of deep learning, are a before-and-after in the history of computer science. Pooling layers are one of the main components of Convolutional Neural Networks (CNNs). They are designed to compact information, i.e. reduce data dimensions and parameters, thus increasing computational efficiency. Since CNNs work with the whole image, the number of neurons increases and so does the computational cost. For this reason, some kind of control over the size of our data and parameters is needed. However, this is not the only reason to use pooling methods, as they are also very important to perform a multi-level analysis. This means that rather than the exact pixel where the activation happened, we look for the region where it is located. Pooling methods vary from deterministic simple ones, such as max pooling, to probabilistic more sophisticated ones, like stochastic pooling. All of these methods have in common that they use a neighborhood approach that, although fast, introduce edge halos, blurring and aliasing. Specifically, max pooling is a basic technique that usually works, but perhaps too simple since it neglects substantial information applying just the max operation on the activation map. On the other hand, average pooling is more resistant to overfitting, but it can create blurring effects to certain datasets. Choosing the right pooling method is key to obtain good results.

Recently, wavelets have been incorporated in deep learning frameworks for different purposes [3, 4, 8], among them as pooling function [8]. In [8], the authors propose a pooling function that consists in performing a 2nd order decomposition in the wavelet domain according to the fast wavelet transform (FWT). The authors demonstrate that their proposed method outperforms or performs comparatively with traditional pooling methods.

In this article, inspired by [8], we explore the application of different wavelet transforms as pooling methods, and then, we propose a new pooling method based on the best combination of them. Our work differs with [8] mainly in three aspects: 1. We perform 1st order decomposition in the wavelet domain according to the discrete wavelet transform (DWT), and therefore, we can extract directly the images from the low-low (LL) sub-band, 2. We explore different wavelets transforms instead of using only Haar wavelet, and 3. We propose a new pooling method based on the combination of different wavelet transforms.

The organization of the article is as follows. In Sect. 2, we present the Multiple Wavelet Pooling methodology and in Sect. 3, we present the datasets, the experimental setup, discuss the results and describe the conclusion.

Fig. 1.

Overview of multiple wavelet pooling

2 Multiple Wavelet Pooling

Wavelet transform is a representation of the data, similar to the Fourier transform, that allows us to compact information. Given a smooth function f(t), the continuous case is defined as

$$ CWT_{(s, l)}f = s^{-1/2} \int f(t) \psi \left( \frac{t - l}{s}\right) dt. $$

where $\psi (t)$ is a mother wavelet and $s \in \mathbb {Z}$ is the scale index and $l \in \mathbb {Z}$ is the location index. Given an image A of size (n, n, m), the finite Discrete Wavelet Transform (DWT) can be achieved building a matrix, as explained in [2]:

$$ W = \begin{pmatrix} H \\ \hline G \end{pmatrix}, H = \begin{pmatrix} h_0 &{} h_1 &{} \cdots &{} h_{n-2} &{} h_{n-1} \\ h_{n-2} &{} h_{n-1} &{} \cdots &{} h_{n-4} &{} h_{n-3}\\ \vdots &{} \vdots &{} \ddots &{} \vdots &{}\vdots \\ h_2 &{} h_3 &{} \cdots &{} h_0 &{} h_1 \end{pmatrix} , G = \begin{pmatrix} g_0 &{} g_1 &{} \cdots &{} g_{n-2} &{} g_{n-1} \\ g_{n-2} &{} g_{n-1} &{} \cdots &{} g_{n-4} &{} g_{n-3}\\ \vdots &{} \vdots &{} \ddots &{} \vdots &{}\vdots \\ g_2 &{} g_3 &{} \cdots &{} g_0 &{} g_1 \\ \end{pmatrix} $$

Note that H and G are submatrices of size $(\frac{n}{2}, n, m)$ and

The original image A is transformed into 4 subbands: the LL subband is the low resolution residual which consists of low frequency components, which means that it is an approximation of our original image; and thee subbands HL, LH and HH give horizontal, vertical and diagonal details, respectively.

In this article, we propose to form the pooling layer by combining different wavelets: Haar, Daubechie and the Coiflet [1] one. Haar basis is formed by $h = (1 / \sqrt{2}, 1 / \sqrt{2})$ and $g =(1 / \sqrt{2}, -1 / \sqrt{2})$; the Daubechies basis is formed by $h = ((1 + \sqrt{3})/4\sqrt{2}, (3 + \sqrt{3})/4\sqrt{2}, (3 - \sqrt{3})/4\sqrt{2}, (1 - \sqrt{3})/4\sqrt{2})$ and $g = ((1 - \sqrt{3})/4\sqrt{2}, (-3 + \sqrt{3})/4\sqrt{2}, (3 + \sqrt{3})/4\sqrt{2}, (-1 - \sqrt{3})/4\sqrt{2})$; and finally the Coiflet basis is formed by $h = (-0.0157, -0.0727, 0.3849, 0.8526, 0.3379, -0.0727)$ and $g = ( -0.0727, -0.3379, 0.8526, -0.3849, -0.0727, -0.0157)$. From these, you can populate the wavelet matrix following the Lemma 3.3 and Theorem 3.8 in [2].

The algorithm for multiple wavelet pooling is as follows:

• 1. Choose two different wavelet bases and compute their associated matrices, $W_1$ and $W_2$.

• 2. Present the image feature F and perform, in parallel, the two associated discrete wavelet transforms $W_1 F W_1^T$ and $W_2 F W_2^T$.

• 3. Discard HL, LH, HH from every matrix, thus only tacking into account the approximated image $LL_1$ and $LL_2$ by the two different basis.

• 4. Concatenate both results and pass on to the next layer.

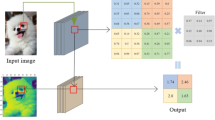
In Fig. 1, we can see an example of how this pooling method works within a CNN architecture.

3 Results and Conclusions

We used three different datasets for our testing: MNIST [6], CIFAR-10 [5] and SVHN [7]. In order to compare the convergence, we use the categorical entropy loss function; as a metric, we use the accuracy. For the MNIST dataset, we used a batch size of 600, we performed 20 epochs and we used a learning rate of 0.01. For the CIFAR-10 dataset, we performed two different experiments: one without dropout, with 45 epochs and one with dropout, with 75 epochs. For both cases, we used a dynamic learning rate. For the SVHN dataset, we performed a set of experiments with 45 epochs and a dynamic learning rate. All CNN structures are taken from [8] for the respective datasets. In this case, we test algorithms without dropout to observe the pooling method’s resistance to overfit. Only in the case of CIFAR-10, we take into account both performances with and without dropout.

Table 1 shows the accuracies obtained for each pooling method together with their position on the ranking; additionally, we highlight in bold the best performance for each dataset. We will denote “d” the case when we perform the model training with dropout. For the MNIST data-set, the choice of the Daubechie basis improves the accuracy, compared to the Haar basis. For CIFAR-10 and SVHN, we can see that the multiple wavelet pooling performed evenly or better than max and average pooling. Specially, for the case with dropout, the multiple wavelet pooling algorithm outperformed all other pooling algorithms.

Table 1. Accuracy obtained for each pooling method together with the ranking position. We highlight with boldface the three best results for each dataset. The last column represents the mean rank of each pooling method across all datasets

In Fig. 2 (left), we present an example of the convergence of every pooling method compared. In general lines, the multiple wavelet algorithm always converges faster or comparatively to max and average pooling. Simple wavelet pooling, for any of its variants, is always the second fastest convergence method.

Fig. 2.

SVHN loss function (left) and Multiple wavelet Haar + Daubechie results (right)

In Fig. 2 (right), we show an example of predictions for the SVHN dataset with Haar and Daubechie basis. The first row represents correct predictions, the second row represents wrong predictions. The network has trouble distinguishing images where more than one digit appears. Still, it is very consistent: the first, second, third and fifth images could be considered to be correct.

In conclusion, we proved that multiple wavelet pooling are capable of competing and outperforming the well-known max and average pooling: yielding better results and at the same time converging faster.