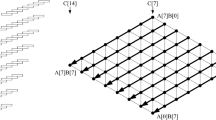
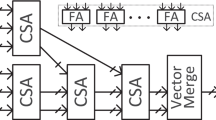
Abstract
For the pre/post-quantum Public Key Cryptography (PKC), such as Elliptic Curve Cryptography (ECC) and Supersingular Isogeny Diffie–Hellman key exchange (SIDH), modular multiplication is the most expensive operation among basic arithmetic of these cryptographic schemes. For this reason, the execution timing of such cryptographic schemes in an implementation level, which may highly determine the service availability for the low-end microprocessors (e.g., 8-bit AVR and 16-bit MSP430X), is mainly relied on the efficiency of modular multiplication on the target processors.
In this paper, we present new optimal modular multiplication techniques based on interleaved Montgomery multiplication on 16-bit MSP430X microprocessors, where the multiplication part is performed in a hardware multiplier and the reduction part is performed in a basic Arithmetic Logic Unit (ALU) with optimal modular multiplication routine, respectively. This approach is effective for special modulus of NIST curves, SM2 curves, and SIDH. In order to demonstrate the superiority of proposed Montgomery multiplication, we applied the proposed method to the NIST P–256 curve, of which the implementation improves the previous modular multiplication and squaring operations by 39% and 37.1% on 16-bit MSP430X microprocessors, respectively. Moreover, secure countermeasures against timing attack and simple power analysis is also applied to the scalar multiplication of NIST P–256, which achieves the 9,285,578 clock cycles and only requires 0.575 s (@16 MHz). The proposed Montgomery multiplication has broad applications to other cryptographic schemes and microprocessors.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
SM2 curve also has similar special patterns of modulus (0xFFFFFFFEFFFFFFFF FFFFFFFFFFFFFFFFFFFFFFFF00000000FFFFFFFFFFFFFFFF).
References
FIPS 186-2: Digital signature standard (DSS). Federal Information Processing Standards Publication 186–2, National Institute of Standards and Technology (2000)
Adalier, M.: Efficient and secure elliptic curve cryptography implementation of Curve P-256. In: Workshop on Elliptic Curve Cryptography Standards (2015)
Düll, M., et al.: High-speed Curve25519 on 8-bit, 16-bit, and 32-bit microcontrollers. Des. Codes Crypt. 77(2–3), 493–514 (2015)
Faz-Hernández, A., López, J., Ochoa-Jiménez, E., Rodríguez-Henríquez, F.: A faster software implementation of the supersingular isogeny Diffie-Hellman key exchange protocol. IEEE Trans. Comput. 67(11) (2017)
Gouvêa, C.P., Oliveira, L.B., López, J.: Efficient software implementation of public-key cryptography on sensor networks using the MSP430X microcontroller. J. Cryptogr. Eng. 2(1), 19–29 (2012)
Gueron, S., Krasnov, V.: Fast prime field elliptic-curve cryptography with 256-bit primes. J. Cryptogr. Eng. 5(2), 141–151 (2015)
Hinterwälder, G., Moradi, A., Hutter, M., Schwabe, P., Paar, C.: Full-size high-security ECC implementation on MSP430 microcontrollers. In: Aranha, D.F., Menezes, A. (eds.) LATINCRYPT 2014. LNCS, vol. 8895, pp. 31–47. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16295-9_2
Jalali, A., Azarderakhsh, R., Kermani, M.M., Jao, D.: Supersingular isogeny Diffie-Hellman key exchange on 64-bit ARM. IEEE Trans. Dependable Secure Comput. (2017)
Koziel, B., Jalali, A., Azarderakhsh, R., Jao, D., Mozaffari-Kermani, M.: NEON-SIDH: efficient implementation of supersingular isogeny Diffie-Hellman key exchange protocol on ARM. In: Foresti, S., Persiano, G. (eds.) CANS 2016. LNCS, vol. 10052, pp. 88–103. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-48965-0_6
Liu, Z., Seo, H., Castiglione, A., Choo, K.K.R., Kim, H.: Memory-efficient implementation of elliptic curve cryptography for the Internet-of-Things. IEEE Trans. Dependable Secure Comput. (2018)
Liu, Z., Seo, H., Großschädl, J., Kim, H.: Efficient implementation of NIST-compliant elliptic curve cryptography for 8-bit AVR-based sensor nodes. IEEE Trans. Inf. Forensics Secur. 11(7), 1385–1397 (2016)
Peters, D., Raskovic, D., Thorsen, D.: An energy efficient parallel embedded system for small satellite applications. ISAST Trans. Comput. Intell. Syst. 1(2), 8–16 (2009)
Rivain, M.: Fast and regular algorithms for scalar multiplication over elliptic curves. IACR Cryptology Eprint Archive (2011)
Seo, H.: Compact software implementation of public-key cryptography on MSP430X. ACM Trans. Embed. Comput. Syst. (TECS) 17(3), 66 (2018)
Seo, H., Kim, H.: Multi-precision squaring on MSP and ARM processors. In: 2014 International Conference on Information and Communication Technology Convergence, ICTC, pp. 356–361. IEEE (2014)
Seo, H., Lee, Y., Kim, H., Park, T., Kim, H.: Binary and prime field multiplication for public key cryptography on embedded microprocessors. Secur. Commun. Netw. 7(4), 774–787 (2014)
Seo, H., Shim, K.A., Kim, H.: Performance enhancement of TinyECC based on multiplication optimizations. Secur. Commun. Netw. 6(2), 151–160 (2013)
Walter, C.D., Thompson, S.: Distinguishing exponent digits by observing modular subtractions. In: Naccache, D. (ed.) CT-RSA 2001. LNCS, vol. 2020, pp. 192–207. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45353-9_15
Zhou, L., Su, C., Hu, Z., Lee, S., Seo, H.: Lightweight implementations of NIST P-256 and SM2 ECC on 8-bit resource-constraint embedded device. ACM Trans. Embed. Comput. Syst. (TECS) (2018)
Acknowledgement
This work was partly supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. NRF-2017R1C1B5075742) and the MSIT(Ministry of Science and ICT), Korea, under the ITRC (Information Technology Research Center) support program (2014-1-00743) supervised by the IITP (Institute for Information & communications Technology Promotion). The work of Zhi Hu is partially supported by the Natural Science Foundation of China (Grant No. 61602526).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Seo, H., An, K., Kwon, H., Hu, Z. (2019). Compact Implementation of Modular Multiplication for Special Modulus on MSP430X. In: Lee, K. (eds) Information Security and Cryptology – ICISC 2018. ICISC 2018. Lecture Notes in Computer Science(), vol 11396. Springer, Cham. https://doi.org/10.1007/978-3-030-12146-4_4
Download citation
DOI: https://doi.org/10.1007/978-3-030-12146-4_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-12145-7
Online ISBN: 978-3-030-12146-4
eBook Packages: Computer ScienceComputer Science (R0)