Abstract
We outline an artificial perception model for an algorithm that detects junctions in casual sketches. These sketches are used by skilled individuals to visually and quickly convey ideas.
The new algorithm detects junctions in 2D, before any 3D model is available. Tips of line segments are merged into 2D junctions that are assumed to depict 3D vertices. The current scope is limited to line-drawings of polyhedral objects vectorized from sketches. The process mainly uses information that is available in the neighborhood of the candidate junction. The algorithm calculates a figure of merit that estimates how likely a junction is to be perceived as such.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
People use sketches because they convey visual information that can readily be perceived by humans (although not so readily by computers). Junctions are not necessarily contained explicitly in the original sketch or automatically obtained at the vectorization stage.
In this paper, we describe and assess an improved approach for merging tips of vectorized lines to produce 2D junctions (points where the tips of the lines meet) that depict 3D vertices (points where the edges of polyhedral shapes meet). The input for our vertex-merging approach is a set of vectorized line segments (or simply “lines”) delimited by their tips. Then, vertex detection must merge dangling tips to determine junctions that depict valid vertices. The output is a line-drawing: a list of lines and a list of junctions, where each line connects two junctions. Junctions are (x, y) coordinate pairs of shared endpoints that likely correspond to vertices of the depicted object.
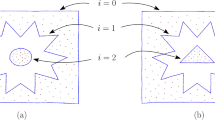
We distinguish careful and casual sketches (also called detailed and quick sketches). Examples of both types of sketches are provided in Fig. 1. Based on the classification of sketches defined by Ferguson [5], we assume that thought sketches are usually casual, while prescriptive sketches tend to be more careful.
The algorithm does not assert “this is a vertex” but “this is more or less likely to be a vertex”. In this regard, we provide a candidate beautified line drawing for a subsequent global perception mechanism based on our hypothesis that a local intersection of a set of strokes which can barely be accepted as depicting a common junction when perceived separately, may be seen as a valid vertex when put into context (see, for instance, the lower left junction in example of Fig. 1, right).
2 Related Work
Approaches to drawing vectorization and beautification typically include endpoint snapping strategies (like the intersection detection in [7]).
Optimization based formulations [4], or machine learning techniques (such as convolutional network approaches [11]) are necessarily global approaches. Training a machine learning system with abstract drawings that do not represent any perceivable shape would be unrealistic, while using sketches that depict shapes necessarily forces the trainer to use—even unconsciously—her global perception to judge the particular junctions.
Instead, our goal is to improve the approach of determining a linearly decreasing likelihood for tip snapping based on the distance between tips [6]. A similar approach was recently proposed by Liu et al. to simplify over-traced sketches [9]. Similarly to Liu et al., we have also adopted a strategy based on proximity and continuity, but also closure.
Finally, detecting whether a user is drawing carefully or casually is feasible—see, for instance, recent efforts to use the design intent embedded in the features of the product to quantify uncertainty [3]. However, sketches may contain a mixture of casual and careful junctions. Therefore, by assuming that both junction types must be detected, a bi-fold approach was adopted.
3 Proposed Approach
Two main ideas are combined in the new approach: (1) well-known Gestalt Principles must guide the perception of the junctions, and (2) the strategy must manage both careful and casual sketches.
Careful sketches are based on reification: the action of perceiving the tips of two or more lines as representing one single junction. By applying the Gestalt law of proximity, two or more carefully drawn tips that are close to each other are to be reified as a single junction (Fig. 1, left). The way this rule applies is explained in detail by Hoffman’s rule #2, “if the tips of two lines coincide in an image, then always interpret them as coinciding in 3D”, and #4 “Interpret elements nearby in an image as nearby in 3D” [8].
For casual sketches, the driving idea is emergence, i.e., tips are presumed to be imprecise, thus junctions must emerge, not at the tips of the lines but at the intersections between the lines (or their extensions). In this case, the law of closure dominates (Fig. 1, right). As stated by Hoffman’s rule #13, “if three or more curves intersect at a common point in an image interpret them as intersecting at a common point in space” [8].
The goodness of the detected junctions must be quantified by a figure of merit, which is in the range [0, 1]. 1 means that the junction is to always be perceived as such by humans; 0 means that humans will hardly ever perceive the junction.
The full source code of the algorithm is freely available at [2], including examples that demonstrate the capabilities and limitations of the approach.
3.1 Reification of Careful Vertices
The classic nearest-neighbor criterion of merging tips by determining their distances to one another is used by our approach to merge junctions that represent vertices defined by carefully drawn lines. To this end, the Delaunay triangulation of the set of tips is calculated by using an adapted version of the Dumoulin C++ implementation of the algorithm by Bourke [1]. Next, for each tip, those other tips that share at least one triangle with it are labeled as neighbors, unless they also share one line. Finally, the neighboring tips are checked to determine whether they are close enough to be merged. This strategy is fast and favors finding trihedral junctions. Some junctions of the external outline, or of higher valence, may not get completely reified (thus forcing the later emergence process to complete them). The method was improved in a number of ways.
First, we consider the perceptual principle that longer lines usually belong to main features—which are perceived first—whereas shorter lines are usually perceived as belonging to secondary details. Thus, the algorithm searches for junctions between longer lines first.
Second, errors that are acceptable in the location of the tips tend to be proportional to the total length of each line: errors in the location of the tips of longer lines are accepted to be greater in absolute value than those of shorter lines. Thus, the threshold distance between the tip and the candidate junction is defined as a percentage of the length of each line.
Third, since the sketches are assumed to depict orthographic representations of flat figures or pictorial representations of polyhedral shapes, the range between right angles and cubic corners (see [10] for a definition of cubic corners) is prioritized. To this end, an anisotropic merging area is defined around each tip (see Fig. 2 left, where the tip \(v_{2}\) of line \(e_{2}\) must be closer than \(v_{3}\) to be labeled as close enough to merge with \(v_{1}\)). The merging area depicted in Fig. 2 left is merely illustrative, since the intersection between the lines may not necessarily be coincident with any of the tips. Therefore, the distance allowed between two lines (\(e_{1}\) and \(e_{2}\) in Fig. 2 right) is calculated and then compared to the actual distance between their tips. The allowed distance (\(r_{2}\) in Fig. 2 right) is calculated as the product of a threshold maxDist (fixed at 8% of the length of the line) and an \(allowance=2-cos(e_{i}, e_{j})\). The allowed distance (maxDist*allowance) is at its maximum value for 90\(^{\circ }\) (20%), and still high for 60\(^{\circ }\) (15%). In axonometric views squared lines are commonly depicted by lines at angles close to 60\(^{\circ }\).
The allowance penalizes merging tips of collinear lines that are poorly drawn. Naturally, collinear lines are uncommon in polyhedral vertices and non collinear lines are seldom depicted as collinear (as this situation would conflict with Hoffman’s rule #3 “Always interpret lines collinear in an image as collinear in 3D” [8]). By using the allowance to calculate the merits of the candidate junctions, the merging of perpendicular lines is prioritized.
If tip \(v_{2}\) is sufficiently close to \(v_{1}\) (this is, if \(|v_{1}-v_{2}| < |r_{2}|\), where \(|r_{2}|\) depends on the relative orientation between \(e_{1}\) and \(e_{2}\)) the intersection of the two segments is defined as the common merged tip, regardless of whether or not this new tip falls outside the merging area (Fig. 2 right). This way, lines are prevented from rotating while merging their tips.
Up to this point, our approach assumes that tips of vectorized lines are not yet connected to each other, i.e., the valence (number of lines that share the tip) is 1 for all the tips. However, this is not the case when the merging-vertices algorithm progresses, as tips that have already been visited may be partially merged. Therefore, the goal is to prioritize the most populated junctions. The general rules to cluster tips of valence other than 1 are as follows: (1) If valences are different for both tips, the tip with the highest valence remains fixed while the other is moved to the cluster, (2) If valences are equal (and different from 1) both tips are moved to the cluster into the midpoint they define. A clustering threshold is defined to prevent lines from excessive rotation. A merge is declared valid if all the lines connected to the moving tip rotate less than maxRot (fixed at 10\(^{\circ }\)) when redirected to the new tip.
Therefore, the merit of reified junctions is assigned \(-1\) if tips are separated more than the allowed distance or the maximum rotation of any line exceeds maxRot. Otherwise, the merit of reified junctions is in the range average-to-good, calculated as a fixed minimum reward for careful junctions RM (fixed at 0.50), plus two variable components. The first variable component, which depends on the distance merit, equals RD if both tips are coincident, and decreases linearly to 0 for tips separated by the allowed distance (maxDist*allowance). The second variable component depends on the rotations: it equals RR if no line rotates to merge the tips, and linearly decreases to 0 if the maximum rotation of any line equals maxRot. To ensure that the merits of valid junctions are in the range [0, 1], RD is fixed as \((1-RM)\), and RR is null, for lines with valence 1. For other lines, both RD and RR are fixed as \((1-RM)/2\).
3.2 Emergence of Casual Vertices
Two rules apply to help the emergence of junctions at the intersections between casual lines (or their extensions).
First, Hoffman’s rule #13 is used to prioritize trihedral junctions as follows: three dangling lines that intersect close to each other, and close to their tips, define a new junction (Fig. 1 left). The maximum allowed distance between intersections is maxDistTriplets (set to 10% of the length of the longest line in the triplet). The distance from the intersection to the tips must fit in a valid range. It may not be longer than inTol (50%) of the average length of the three candidate lines for intersections inside the segment, and no longer than outTol (25%) of the average length of the three candidate lines for intersections in the extension of the segment. Assigning an asymmetric range (\(inTol> outTol\)) prioritizes intersections inside the segments, which was experimentally determined to be the common perceptual behavior.
The intersections must be the closest to the tips in order to prevent false merges such as the one illustrated in Fig. 3, left. In this case, semi-line \(e_{1}\) could be incorrectly merged with semi-lines \(e_{0}\) and \(e_{2}\) if they were processed from longer to shorter. The three semi-lines that intersect close to each other are connected to a common junction located at the centroid of the three intersection points (Fig. 3, middle). The merit of the emerged triple junction is in the range [0, ETM], since it is assigned as \(ETM*(1-distCentroid/maxDistTriplets)\), where distCentroid is the distance between the centroid and the most distant intersection point. In our implementation, ETM is fixed as 0.5, to ensure that the merits of emerged junctions are in the average-to-poor range. Next, a relaxed search is performed after removing the condition that intersections must be the closest ones to the tips. This provides a second chance for detecting those casual triplets that are close to each other and include long lines (which are parsed first) that are more casual than the short ones.
Triplets should only merge semi-lines that intersect closer to the tips (left), while the centroid of the intersections between three dangling lines emerges as a junction (middle), and a line that needs excessive rotation to merge to the original neighboring tips can merge when relaxing rotation (right).
Second, emergence is also considered by clustering dangling lines to nearby junctions, i.e., a dangling line that passes closely to a junction of valence two or higher must be clustered to it. “Passing closely” implies that the distance between the line and the junction (such as \(d_{3}\) in Fig. 3 right) is less than maxDistDangling, which is set to a percentage (10%) of the length of the dangling line. An allowed distance (maxDistDangling*allowance) is used where the allowance is calculated between the dangling line and its most collinear line in the junction (i.e. lowest allowance between the dangling line and each of the lines in the junction). It also implies that the point of perpendicular projection of the junction on the semi-line must fit in the valid range: inTol of its length from the tip of the semi-line if it is inside the segment (t in Fig. 3 right), or outTol if it is in the extension of the segment.
The merit for dangling lines merged to junctions (EDM) is calculated as the minimum of two components: first, merit is 1 for dangling lines passing over the junction, and decreases down to 0 for lines passing at a distance of maxDistDangling. Second, merit is 1 for dangling lines where the closest point to the junction is the tip of the dangling line, and decreases linearly for lines whose closest point to the junction is at the limit of the valid range. Dangling lines with negative merit are not merged. As a result, the new merit assigned to the junction where a dangling line is merged is the minimum between the current merit of the junction and the merit of merging the dangling line to the junction.
4 Validation
A total of 91 subjects (17 from Spain, 61 from the US, and 13 from Italy) were interviewed. Most subjects had an engineering background (18 were engineering educators and 73 engineering students). Participants were asked to casually sketch the models shown in Fig. 4.
Incorrect sketches included: (a) missing strokes, (b) dashed hidden lines, (c) ignored short beautification strokes and (d) overtraced sketches. We discarded 44 sketches from model 1, 25 from model 2, 24 from model 3 and 43 from model 4 (all from engineering students). Model 4 frequently included missing lines, most likely because of its complexity, while missing lines in Model 1 where possibly due to its viewpoint or orientation.
The participants’ sketches were vectorized by the authors and the line drawings parsed against the “ground truth” of the vertices of the models. Since the subjects were asked to replicate four particular models, we assume they tried to replicate the junctions of the model. Our algorithm was used to calculate which of those junctions were more or less frequently detected. From the analysis of the frequencies with which vertices of each model were recognized correctly, we can conclude that:
-
The algorithm does not fail in recognizing all “carefully” drawn vertices.
-
The algorithm always assigns merits greater than 0.5 to careful vertices.
-
For imperfect vertices, the assigned merits are in the range [0, 0.5].
-
The algorithm tends to leave lines without converging to a vertex (dangling lines) before making false convergences. In borderline cases of particular points of view (such as Model 1) the algorithm becomes more sensitive to casual vertices.
-
When the drawing contains strokes of very different lengths (Model 4), the algorithm finds it difficult to group the short vertices correctly.
-
The algorithm is not susceptible to the direction in which the strokes are drawn. The general metrics we used eliminate the possible bias that could be introduced by drawing with the right or left hand.
5 Conclusions
Our hypothesis that carefully sketched vertices must be reified, while casually sketched vertices must emerge, was indirectly validated, as it guided the design and implementation of an algorithm that improves on previous vectorization techniques, which were based exclusively on reification strategies.
The perceptual essence of the algorithm combined with sequential detection provides efficiency. The algorithm detects and fixes the best defined junctions, and only applies more complex calculations to poorly defined vertices.
Our approach quickly and correctly detects vertices in line drawings of polyhedral objects that have been vectorized from hand-drawn sketches. Vertices of polyhedral shapes depicted by highly casual sketches can still be detected provided that the sketch does not contain extremely close junctions. In addition, our tests suggest that our method, if re-tuned, may also be useful for other sketched shapes.
We are confident that the set of metrics based on relevant geometric features derived from studies on human perception, along with the required global scene information, may feed a future machine learning approach to further improves the current success ratio of our approach. However, since the approach still relies on an excessively large set of parameters, further studies are needed to determine whether a reduced set of independent parameters can be defined.
References
Bourke, P.: Triangulate: efficient triangulation; algorithm suitable for terrain modelling. In: Pan Pacific Computer Conference (1989). http://paulbourke.net/papers/triangulate/. Accessed June 2018
Company, P., Plumed, R., Varley, P., Camba, J.: Finding vertices in 2D line-drawings of polyhedral shapes (2018). http://www.regeo.uji.es/FindingVertices.htm, geometric Reconstruction Group, http://www.regeo.uji.es
Ekwaro-Osire, S., Cruz-Lozano, R., Endeshaw, H., Dias, J.: Uncertainty in communication with a sketch. J. Integr. Des. Process. Sci. 20(4), 43–60 (2016)
Favreau, J., Lafarge, F., Bousseau, A.: Fidelity vs. simplicity: a global approach to line drawing vectorization. ACM Trans. Graph. 35(4) (2016). Article No. 120
Ferguson, E.: Engineering and the Mind’s Eye. The MIT Press, Cambridge (1992)
Fišer, J., Asente, P., Schiller, S., Sýkora, D.: Advanced drawing beautification with shipshape. Comput. Graph. 2(56), 46–58 (2016)
Governi, L., Furferi, R., Palai, M., Volpe, Y.: 3D geometry reconstruction from orthographic views: a method based on 3D image processing and data fitting. Comput. Ind. 2(64), 1290–1300 (2013)
Hoffman, D.: Visual Intelligence: How We Create What We See. W.W. Norton & Company, New York (1998)
Liu, X., Wong, T., Heng, P.: Closure-aware sketch simplification. ACM Trans. Graph. 34(6) (2015). Article No. 168
Perkins, D.: Cubic Corners, Oblique Views of Pictures, the Perception of Line Drawings of Simple Space Forms. Geometry and the Perception of Pictures: Three Studies. Technical report, Harvard University, Cambridge, Mass. Graduate School of Education (1972). files.eric.ed.gov/fulltext/ED114328.pdf
Simo-Serra, E., Iizuka, S., Sasaki, K., Ishikawa, H.: Learning to simplify: fully convolutional networks for rough sketch cleanup. ACM Trans. Graph. 35(4) (2016)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Company, P., Varley, P.A.C., Plumed, R., Camba, J.D. (2019). Detection of Vertices in Sketched Drawings of Polyhedral Shapes. In: Vera-Rodriguez, R., Fierrez, J., Morales, A. (eds) Progress in Pattern Recognition, Image Analysis, Computer Vision, and Applications. CIARP 2018. Lecture Notes in Computer Science(), vol 11401. Springer, Cham. https://doi.org/10.1007/978-3-030-13469-3_44
Download citation
DOI: https://doi.org/10.1007/978-3-030-13469-3_44
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-13468-6
Online ISBN: 978-3-030-13469-3
eBook Packages: Computer ScienceComputer Science (R0)