Keywords

1 Introduction

Shape is a classical attribute used in different tasks of computer vision. It is one of the most important features for object recognition with first studies dated from the 60’s [1]. Furthermore, one of the interests in this feature is inspired by biological problems where shape characteristics are necessary [6].

Many methods for shape classification have been proposed in the literature. These methods can be divided into three main categories [14]: skeleton-based, region-based and contour-based techniques. The category of a method is related to the process used to extract the features from the shape. In this sense, skeleton-based methods use the medial axes of the shape for characterization and have as advantage the robustness for shapes with occlusion (e.g. [2, 5]). On the other hand, region-based techniques use the whole image to characterize the shapes. Examples of this category are Zernike moments [23] and Hu moments-based methods [12]. The last category, uses contour information of the shape for characterization (e.g. Fourier descriptors [21], Curvature Scale Space [15] and multi-scale fractal dimension [20]). However, many methods of this category suffer when the silhouette is degraded. Recently, methods based on complex networks have been proposed to analyze shapes [3, 18, 19] and to deal with non-perfect contours that are often found in biological problems.

In this paper, we proposed a novel method for shape analysis based on the deterministic partially self-avoiding walk (DPSW) on networks. To accomplish this task, the shape contour is modeled as a network, including the information about the distribution of the contour pixels in the image. Then, we apply the DPSW on the network and use statistical measurements about the trajectories to obtain a shape signature, which can be used to distinguish different classes of shapes. The proposed method was applied on biological shape classification, which is a changeling problem, due to the diversity found in nature. Experiments results on the two natural databases showed the effectiveness of the proposed method compared to other shape methods.

This paper is organized as follows. Section 2 describes the proposed method to obtain a shape signature. Then, Sect. 3 presents the results obtained by the proposed method and others. Finally, in Sect. 4, the conclusions of the work are drawn.

2 Proposed Method

2.1 Modeling Contour as Network

Different approaches have been proposed to model contour as network [3, 19]. Based on this, we model the contour as follows. Let a network represented by a set of vertices \(V = \{v_1, v_2, ...,v_n\}\) and a set of edges E where each edge \(e_{v_i,v_j}\) connects two vertices \(v_i\) and \(v_j\). The neighbors of a vertex are given by \(\nu (v)\). Now, consider a set of pixels S of size N that belong to the contour C of a shape. Each pixel \(s_i \in S\) is represented by discrete numerical values \(s_i = (x_i,y_i)\) representing its Cartesian coordinates. To build a network, each point of the contour \(s_i \in S\) is mapped into a vertex \(v_i \in V\) of the network. Then, we connected each pair of vertices with a non-directed edge. For each edge \(e_{v_i,v_j}\) is attributed a weight \(w(e_{v_i,v_j})\) according to the Euclidean distance considering the coordinates of the pixels \(s_i\) and \(s_j\) represented by the vertices \(v_i\) and \(v_j\), \(w(e_{v_i,v_j}) = \sqrt{(x_i-x_j)^2 + (y_i-y_j)^2}\). The edges weights are normalized by the largest distance between all pixels \(w_{max}\) of the contour, \( w(e_{v_i,v_j}) = \frac{w(e_{v_i,v_j})}{w_{max}}\). This normalization aims to keep the edges weights in the interval [0, 1] and invariant to scale of the shape.

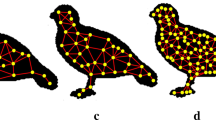
At the moment, the network presents a regular behavior, i.e., all vertices have the same degree. Thus, it is necessary to apply a procedure to transform the network and to reveal important characteristics [17]. To accomplish this task, a simple and widely used approach is to apply a threshold t to remove edges. In this approach, a new network \(G_t = (V_t,E_t)\) is obtained for each value of threshold t (Fig. 1(a)). Therefore, the transformed network \(G_t\) is obtained removing all edges of E whose the weight is equal or smaller than t, \(E_t = \{e_{v_i,v_j} \in E | w(e_{v_i,v_j}) \le t \}\).

Each value of t highlights different patterns of the network topology. In this way, we use different threshold values to achieve a richer set of measurements that describe the network dynamics [7, 9]. Thus, the network characterization is performed using a set of thresholds T, which is defined by an initial threshold \(t_0\), an incremental threshold \(t_i\) and a final threshold \(t_f\).

Fig. 1.
figure 1

(a) Example of the application of different values of threshold in a contour network. (b) Illustration of a DPSW on a network using the \(r=max\), \(\mu =1\) and the vertex degree as criterion of distance. The edges in red represent the movements of the tourist until find the attractor (edges in green). (Color figure online)

Full size image

2.2 Deterministic Partially Self-avoiding Walk on Network

Recently, DPSW has emerged as a promising approach for pattern recognition, obtaining great results in different problems such as texture analysis [4], dynamic texture analysis [8] and synthetic complex networks classification [9]. A DPSW on the network can be interpreted as a tourist that visit N vertices of the network. The tourist starts the walk from a pre-defined vertex \(v_i\) and the rule of movement r to visit the next vertex \(v_j\) is: go to the neighboring vertex that minimizes the distance \(d(v_i,v_j)\) and has not been visited in the previous \(\mu \) steps. In this rule, named as \(r = min\), the tourist moves by minimizing the distances between vertices. On the other hand, in the rule \(r = max\), the tourist maximize the distances between vertices. On networks, it is necessary to define the distance \(d(v_i,v_j)\) between two vertices \(v_i\) and \(v_j\). In this way, we consider two different criterion of distance c: the degree of the neighboring vertex \(d(v_i,v_j) = k_{v_j}\) and the edge weight \(d(v_i,v_j) = w(e_{v_i,v_j})\). It can occur of two neighboring vertices have the same distance, in this case, we consider as tiebreaker: the edge weight for the criterion of degree and the vertex degree for the criterion of the edge weight.

The memory (\(\mu -1\)) is the window in which the tourist performs a deterministic walk partially self-repulsive. In other words, the tourist will consider a visited vertex attractive again after having traveled \(\mu \) vertices. The rule of movement is based on the neighborhood of the vertex \(\nu (v)\) and a short memory \(\mu \), which although simple, can generate DPSW of great complexity [4, 7]. The tourist walk can be divided into two parts: transient and attractor. The transient is the initial part of the walk that has size \(\tau \), and the attractor is the final part of the walk, consisting of a cycle of period \(\rho \ge (\mu + 1)\) in which the attractor gets trapped. The attractor is a cycle of vertices of period \(\rho \) that will always be visited by the tourist, i.e when entering an attractor the tourist cannot escape. Therefore, the transient is the route of the tourist until finding an attractor, where its size \(\tau \) is the number of vertices traveled by the tourist from the initial vertex to the first vertex of the attractor. Figure 1(b) illustrates a trajectory performed by a DPSW. In some cases, depending on the topology of neighboring vertices and the size of memory \(\mu \), it can occur that the tourist does not find an attractor. In this case, the trajectory is considered only by the transient time \(\tau \).

Each vertex of the network is considered as an initial condition to perform a walk. Thus, given a network composed of N vertices, we obtain a set of N trajectories. To measure this set of trajectories performed on the network, a transient time and attractor period joint distribution \(S_{\mu ,r}(\tau ,\rho )\) is used. This distribution combines the transient time \(\tau \) and the attractor period \(\rho \), storing in each position of the distribution the frequency of trajectories with transient \(\tau \) and attractor \(\rho \) [4, 7],

$$\begin{aligned} S_{\mu ,r}^t(\tau ,\rho ) = \frac{1}{N} \sum _{i=1}^{N} \left\{ \begin{matrix} 1,&{} \text {if } \tau _i = \tau \text { and } \rho _i = \rho \\ 0,&{} \text {otherwise} \end{matrix}\right. \end{aligned}$$
(1)

where i is the vertex where the walk was started and t is the value of the threshold applied in the network.

In the last years, several approaches have used features obtained from the joint distribution for classification [4, 7]. In this sense, the histogram \(h_{\mu ,r}^t(l)\) proved to achieve better results in classification tasks. This histogram computes the number of trajectories with size \(l= \tau + \rho \) in a joint distribution calculated with memory size \(\mu \), rule of movement r, value of threshold t and criterion of distance c according to \(h_{\mu ,r}^{t,c}(l)= \sum _{b=0}^{l-1} S_{\mu ,r}^k(b,l-b)\).

In order to construct a feature vector to characterize a shape, we use the n first descriptors of the histogram \(h_{\mu ,r}^{t,c}(l)\). In this work, we define empirically \(n=4\). The first position of the histogram is \((\mu + 1)\) since there is no attractor smaller than \((\mu + 1)\). Thus, the feature vector \(\varPsi (\mu ,r)_t^c\) is given by \(\varPsi (\mu ,r)_t^c = [h_{\mu ,r}^t(\mu + 1), h_{\mu ,r}^t(\mu + 2), ..., h_{\mu ,r}^t(\mu + n)]\). Each rule of movement extracts different properties from the network [9]. Therefore, we combine the feature vector \(\varPsi (\mu ,r)_t^c\) for the two rule of movement. To obtain a robust feature vector, we also concatenate the feature vector \(\varPsi (\mu ,r)_t^c\) for the two criterion of distance (degree and edge weight). Thus, a combined feature vector \(\varUpsilon _{\mu }^t\) is given by \(\varUpsilon _{\mu }^t = [\varPsi (\mu ,min)_t^k, \varPsi (\mu ,max)_t^k, \varPsi (\mu ,min)_t^w, \varPsi (\mu ,max)_t^w]\), where k is the criterion of distance based on degree and w is the criterion of distance based on edges weights.

Earlier works [2, 3, 19] have demonstrated that characteristics of the network dynamic evolution using different values of threshold significantly improves the network topology analysis. In this way, a combined feature vector \(\varPhi _{\mu }\) that considers information of networks transformed by different values of t and uses memory size \(\mu \) is given by: \(\varPhi _{\mu } = [\varUpsilon _{\mu }^{t_0}, \varUpsilon _{\mu }^{t_1}, ..., \varUpsilon _{\mu }^{t_f}]\). Finally, the feature vector \(\varOmega \) is given by concatenating feature vectors \(\varPhi _{\mu }\) for different values of memory size \(\mu \), starting from 0 to the maximum value of memory size \(M_\mu \). This final feature vector is defined as \(\varOmega = [\varPhi _{0}, \varPhi _{1}, ..., \varPhi _{M_{\mu }}]\).

3 Results and Discussion

3.1 Experimental Setup

The proposed method and others were applied on two databases: USPLeaves and Otolith. The USPLeaves [3] database contains images of different species of plants. The classification of this database is a challenging task since that different species of plants have similar shapes and in the digitalization step of the images, overlaps can occur in the adjacency of the objects. This database is composed of 30 leaf species with 20 samples each. The Otolith database is composed of the fish natural database for fish recognition. The database was provided by AFORO [13], which is an open online catalog of otolith images. This database contains 180 different otolith images with 20 different species each.

The literature methods considered for this experiment are: CN Degree [3], Fourier descriptors [16], Curvature descriptors [22], Zernike Moments [23], Multi-Scale Fractal Dimension [20], Segment Analysis [11] and Angular Descriptors of Complex Networks (ADCN) [19]. In order to evaluate the proposed method and other methods, we perform a classification task over its feature vectors using a 10-fold cross-validation scheme and ten repetitions. We use the SVM classifier [10] with a linear kernel, a well-known supervised method.

3.2 Parameter Evaluation

The evaluated parameters of the proposed method are the set of threshold T and the values of memory size \(\mu \). The set of threshold T is defined by an initial threshold \(t_0\), an incremental threshold \(t_i\) and a final threshold \(t_f\). Table 1 presents the classification results for different configurations of \(t_0\), \(t_i\) and \(t_f\). Firstly, we consider \(t_0=0.025\) and \(t_i=0.025\) for different values of final threshold \(t_f\). Note that the best accuracy was obtained for \(t_f = 0.95\). We also note that low values of \(t_i\) provided better accuracies. Thus, we define the values \(t_0=0.025\), \(t_i=0.025\) and \(t_f=0.950\) as the default parameters of the proposed method, since these values obtained good results on the two databases.

Table 1. Accuracies obtained for different set of thresholds.
Full size table

The values of memory size are evaluated in function of the maximum value of memory size \(M_u\) in Table 2. Note that the accuracies tend to decrease or oscillate very little as we increase the value of \(M_\mu \). Also, as we increase the values of \(M_\mu \) the number of features increases as well. In this way, the value \(M_\mu =2\) presents a good tradeoff between performance and number of features on the two databases. Therefore, the final feature vector is given by \(\varOmega = [\varPhi _{0}, \varPhi _{1}, \varPhi _{2}]\).

Table 2. Accuracies for different values of maximum memory \(M_{\mu }\).
Full size table

3.3 Comparison with Other Methods

This section presents a comparison experiment between the proposed method and others (cited in Sect. 3.1). Table 3 shows the accuracies achieved for each shape method evaluated on the two shape databases. For the proposed method, we used the best parameter setting evaluated in Sect. 3.2. For the literature methods, we considered the default parameters defined by the authors. The results showed that the proposed method presents the highest accuracy for both USPLeaves and Otolith databases. On the USPLeaves database, the performance of the proposed method is 3.42% superior to the second best method (C.N. Degree). On the other hand, the proposed method significantly improves the accuracy on the Otolith database when compared to the second best method (Segment Analysis), e.g. from 63.47% to 70.55%. The Otolith database is a much harder classification database due to the presence of little inter-class variability.

Concerning the method based on networks, the proposed method also achieved the highest accuracy on the two databases. On the USPLeaves database, the proposed method improves the accuracy compared to the C.N. Degree and ADCN methods in 3.42% and 9.75%, respectively. On the Otolith database, the proposed method significantly improves correct classification rate compared to the network-based methods, e.g. from 48.08% to 70.55% (C.N. Degree) and from 36.32% to 70.55% (ADCN). These results indicate that the DPSW obtains more significant characteristics of the network for the classification task than other measures.

Table 3. Classification performance of various shape methods on the two databases.
Full size table

4 Conclusion

In this paper, we proposed a novel method for shape classification based on DPSW on networks. After network modeling, DPSWs are performed on networks and statistical measures of the trajectories are used as a signature. These statistical measurements proved to be powerful for shapes classification. In the classification experiments on biological shapes, the proposed method provided better results when compared to other methods. Furthermore, the proposed method outperformed the other network-based methods.