Convolutional Neural Network Architectures for Texture Classification of Pulmonary Nodules

Abstract

Lung cancer is one of the most common causes of death in the world. The early detection of lung nodules allows an appropriate follow-up, timely treatment and potentially can avoid greater damage in the patient health. The texture is one of the nodule characteristics that is correlated with the malignancy. We developed convolutional neural network architectures to classify automatically the texture of nodules into the non-solid, part-solid and solid classes. The different architectures were tested to determine if the context, the number of slices considered as input and the relation between slices influence on the texture classification performance. The architecture that obtained better performance took into account different scales, different rotations and the context of the nodule, obtaining an accuracy of 0.833 ± 0.041.

1 Introduction

Cancer is a disease with great number of deaths worldwide. Recently, estimates indicate that cancer deaths may have exceeded by a narrow margin the deaths from coronary heart disease and strokes [5]. In 2018, 1,735,350 new cancer cases and 609,640 cancer deaths are projected to occur in the United States of America (USA). Lung cancer represents approximately 13% of new cancer occurrences and 26% of cancer deaths, being the leading cause of cancer deaths in the USA for both sexes. The 5-year survival rate of late-stage cancers is approximately 15%, improving with early detection [9]. It is urgent to find new methods to improve the detection, allowing a timely treatment to reduce the current high mortality.

Computerized Tomography (CT) has been the usual imaging modality for monitoring lung cancer due to the good image quality and level of detail. From CT acquisition to the patient’s diagnosis, the steps performed are nodule detection, nodule segmentation, nodule characterization and nodule classification. Nodule detection allows to find the nodule centroid or a bounding box surrounding the nodule region. The estimation of the bounding box facilitates the next steps because the region of interest to analyze is smaller. Since characterization and classification are generally dependent on segmentation, it should be as accurate as possible. The characterization tends to extract data such as volume, Hounsfield units (HU) measures, shape, etc. For classifying the nodule, relevant characteristics are calcification, texture, spiculation, sphericity and margin. Some of these are more easily perceived and are directly related to malignancy, that can be only fully confirmed with biopsy. Lung nodule detection and classification by radiologists only based on the visualization of CT images is a tedious process. Computed-Aided Diagnosis (CAD) systems can help the decision, speeding up the analysis and contributing as a second opinion.

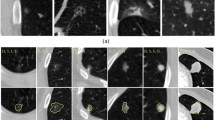
Texture is clearly related to malignancy. The texture classification of lung nodules reflects its internal density and can be labelled unitarily within the interval [1,2,3,4,5]. The solid (S) nodules, those that completely obscure the entire parenchyma, have scores 4 or 5, corresponding to structures clearer than the dark parenchyma. The non-solid/ground glass opacity (GGO) nodules are masses with non-uniformity and intensity similar to parenchyma. They are scored 1 or 2. Part solid nodules (PS) has a score of 3 and consist of a ground-glass with an area of homogeneous soft-tissue attenuation, a solid core [10]. Non-Solid, part-solid and solid have respectively 18%, 63% and 7% of being malignant nodules [6]. This information is also relatively deducible with LungRADS [8]. Figure 1 shows the middle slice of the axial view of nodules with different textures. The red contour represents the expert manual segmentation of the nodule.

Fig. 1.

Nodule Textures: (a) GGO, (b) part-solid and (c) solid.

Some studies have been carried out on the automatic classification of lung nodule texture. In Tu et al. [10], the images correspond to regions of interest (ROI) based on the nodule contours of ground-truth with the expanding offsets of 10 pixels. The images pass through a contourlet transform and a convolutional network with two convolution, two pooling, one fully connected layer and one softmax activation layers. With LIDC dataset, results show concordance with expert opinions and significant performance improvement over histogram analysis. Ciompi et al. [3] implemented a deep learning system based on multi-stream multi-scale convolutional neural network (CNN), which classified nodule as solid, part-solid, non-solid, calcified, perifissural and spiculated. The database was obtained from the Danish Lung Cancer Screening Trial. Due to class imbalance and in order to have data augmentation, the 3D volume was submitted to different number of rotations. The input data was processed by four series of convolutional and pooling layers merging in a final fully-connect layer, before the prediction. The work achieved a classification performance that outperforms the classical methods and is within the inter-observer variability among experts. In the method of Jacobs et al. [7], a KNN classifier was applied to a nodule descriptor constructed based on information of volume, mass and intensity of the segmented nodule. The dataset was from the Dutch-Belgian NELSON lung cancer screening trial. The pairwise agreement between this CAD system and each of expert had a performance in the same range as the interobserver. Cirujeda et al. [4] did a method to classify 3D textured volumes in CT scans as solid, ground-glass opacity and healthy. The 3D descriptor was a covariance-based descriptor with Riesz-wavelet features. The classification model was a “Bag of Covariance Descriptors”. The dataset consists of a private data. The classification performance is computed in terms of sensitivity and specificity with average values of 82.2% and 86.2% respectively.

We develop different CNN architectures to classify the texture of lung nodules. The goal of this work was to infer if the surrounding context of the nodule, the number of slices of the 3D volume considered as input for classification and the relation between the slices have influence on the classification.

2 Material

The used dataset was the Lung Image Dataset Consortium (LIDC-IDRI) [1]. The acquired CTs are composed of parallel axial slices with resolution of $512\times 512$ pixels ranged with spacing of 0.542 to 0.750 mm between pixels. The number of slices varies from 100 to 600 and the thickness from 0.6 to 5 mm. The CTs were analyzed by 4 radiologists, not always the same ones, among the twelve who participated in the study. Table 1 lists the number of nodules per class, number of annotations, and standard deviation of radiologists’ opinion. If more than one radiologist rated the same nodule, it is taken the average of the scores. As the procedure did not require consensus among radiologists, the database contains only 907 (34.0%) nodules are marked from four radiologists. Moreover, the Table 1 shows, on one hand, a large unbalance of classes, on the other hand, that there are 27.1% of cases where the standard deviation is greater or equal than 0.5.

Table 1. Nodule variability in the dataset.

Figure 2 shows an example of the middle axial slice of a nodule and the segmentation defined by different radiologists (Fig. 2(b)–(d)). The attributed scores was, respectively, 3 (part-solid), 4 (solid) and 2 (non-solid). There are only three representations because one radiologist did not consider it as a nodule.

Fig. 2.

Example of a nodule with different segmentations and classifications by radiologists: (a) original image, (b) doctor A, (c) doctor B and (d) doctor C.

Since in the LIDC-IDRI there are different spacings between the acquired voxels, the CTs were resized. The CTs were transformed so that there is a spacing of 0.70 mm between pixels, the most common spacing in the database. The 3D volumes were centered on the nodule and have size of $64\times 64\times 64$ pixels to contain the largest nodule. The intensities were also rescaled for the [−1000 HU, 400 HU] range, which is the range of interest of nodules intensities.

3 Methods

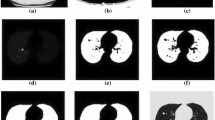
The architectures were designed with the aim of understanding the influence of the context, the number of used slices and the relationship between the slices as CNN input for the texture classification. It is often converted into a classification problem in three classes rather than regression in some works since these labels are most often adopted by radiologists [2]. Figure 3 shows these CNN architectures. The number of input slices can be one (Fig. 3A–B), three (Fig. 3C–D) or even nine (Fig. 3E–F). The architectures of C, E and D, F have, respectively, the same bottom layers of A and B. However, the training is processed independently. The low number of layers, the low number of filters in the convolutional layers and the dropout were strategies used to avoid overfitting. The three slices situation correspond to the three middle slices of the cube. In case of using nine slices, the diagonals of the cube can be used in addition to the middle slices. A scheme representing the extracted slices is shown in Fig. 4.

In what concerns the context importance, CNNs were optimized with input of nodules with and without surrounding context. In the first case, the input are slices extracted directly from the 3D volume while in the second one, the slices of the 3D volume still undergo cropping and resizing so that the borders of the nodule correspond to the limit of the image. This last case was resize to $32\times 32$ pixels since the database has 94.2% nodules with less than 32 pixels in diameter and the input windows with small nodules are not strongly interpolated. The nodule boundaries were defined by the LIDC-IDRI manual markings. The mask consists of the set of pixels in which there is, at least, 50% of the segmentation agreement between radiologists. In Fig. 5, these two inputs with $64\times 64$ pixels and with $32\times 32$ pixels (expanded in the example) are represented.

Fig. 3.

Different used CNN architectures.

Fig. 4.

Representation of used planes: (a) the middle slices and (b) the diagonal slices.

Fig. 5.

Different used input images: (a) without rescaling; (b) with rescaling.

To deal with data imbalance, two strategies were used. In the first, the cube was rotated different number of times per class in the training set (no rotation of solid nodules, 14 rotations of part-solid nodules and 10 rotations of GGO nodules). This also serves as data augmentation. In validation and testing the number of rotations is the same with 8 rotations of 11.25$^{\circ }$ for all classes. The second strategy relies on class weights, that impose a cost dependent on the number of samples per class. These penalties are set in the loss function, which is categorical cross entropy (Eq. 1).

$$\begin{aligned} loss = -\frac{1}{N} \sum _{i=1}^{N} \sum _{j=1}^{M} \alpha _j y_{i,j} log(p_{i,j}) \,\, with\,\,\, \alpha _j = \frac{N}{MN_j} \,\, and \,\,\, N = \sum _{j=1}^{M} {N_j} \end{aligned}$$

(1)

where N is the total data size, M is the number of classes, i is the sample number, j is the class number, $\alpha _j$ is the class weight of a class, $y_{i,j}$ is the one-hot-encoder ground-truth, $p_{i,j}$ is the softmax output of the CNN and $N_j$ is the data size of the class.

Thirteen tests (seven with context and six without context) were performed to take conclusions regarding the proposed goals (Table 2). The 7th hypothesis has, as input, middle slices at different scales (1/3, 2/3, 1 relative to the original) to infer if the multi-scale strategy is able to learn better the features of the small nodules being thus only tested with inputs of $64\times 64$ pixels. A 2.5D approach is called when CNN receives as input more than one slice and it takes into account the relationship between different cube views. For 2D, the class was determined by computed the average of the scores from the used slices.

There was random selection of the LIDC-IDRI database for the training, test and validation sets. 5-times 8-fold cross-validation was used with 20 nodules per class for validation and test. Table 3 shows information about the nodules present in the test set. The algorithm was developed in Keras-TensorFlow. The convergence occurred approximately after 150 epochs. The parameters of the network were optimized using the ADAM algorithm and the learning rate was 0.001. The processor used was Intel (R) Core TM i7-5829K CPU @ 3.30 GHz, the RAM was 32 GB and the GPU was 8 GB.

Table 2. Hypotheses verified with CNN architectures.

Table 3. Informations about the nodules present in the test set.

4 Results

The performance of the method was evaluated using the accuracy. Table 4 shows the results for the different hypothesis previously specified in Table 2.

The results are better when the input is not fitted to the nodule size. As the masks of manual markings were used and they do not fully agree, important information may be lost when the borders of the nodule are fully adjusted to the images limits. On the other hand, it may corroborate the idea that nodule surroundings are important to texture classification. The intensity of the nodule is important but the intensity attenuation at the border and the intensity relative to the background can also be relevant. Probably, 2.5D approaches have better results because the relationships between different views are better understood by the CNN. The best performance happened when the middle slices at different scales were used. The classification probably improved with the use of different scales because of the details in smaller scales, which have less anatomical elements. In general a larger number of slices tend to help to improve nodule classification. This was confirmed by the results of hypothesis 1 and 2. Probably the results have not improved in 3 because it reached a learning plateau in which the increase of number of slices does not improve the accuracy.

Table 4. Accuracy obtained for different architectures.

Figure 6 shows the axial view of the best and the worst results of some nodules for the test set obtained and Table 5 shows accuracy results by class both with the hypothesis 7. The misclassified occurrences correspond to part-solid nodules with a shorter attenuation border and in little situations where there are anatomical elements surrounding the nodule. The solid nodules are not often classified as GGO and vice versa, because they are classes with quite different characteristics.

Fig. 6.

Classification results: (a–c) best results, (d–f) worst results.

Table 5. Accuracy obtained for different classes with the architecture that produced better results.

Although the dataset is the same, this work can not be compared with the Tu et al. [10] because the tested nodules were not available and the ROI were different. In Tu et al. [10], the classification is the average of the score predictions produced for each plane by the 2D CNN. In our proposal the performance of each architecture is measured by a single final score derived from the concatenation of features inside the CNN. Also, the inter-observer calculation could not be done because there were different radiologists in the annotation process. In our opinion, the results and the conclusions that were presented are valid. We believe that the concatenation of features from different slices and a good surrounding context can be a strong contribution to an accurate classification.

5 Conclusion

This work aimed at classifying the texture of lung nodules using different CNN architectures. We were able to conclude that: (1) a larger number of slices extracted from the 3D volume helps to improve the classification; (2) the 2.5D approaches are preferable to 2D because they take into account the relationship between different views of the nodule; (3) context helps a lot in texture characterization; (4) the best performance was verified when different scales were also taken into account. For the future, a 3D approach will be developed and the implemented architectures will be used to solve malignancy classification.