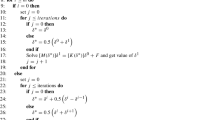Abstract
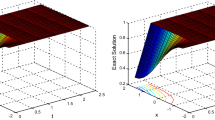
In this paper, the trigonometric cubic B-spline collocation method is extended for the solution of a second order partial integro-differential equations with a weakly singular kernel. The method is obtained by discretization of time derivative using backward finite difference formula while trigonometric cubic B-spline functions are used to approximate the spatial derivative. The scheme is validated through two benchmark test problems. Accuracy of the present approach is assessed in terms of \( L_{\infty } \), \( L_{2} \) error norms and pointwise error. Better accuracy is obtained and the results are compared with quasi wavelet method (QWM), quintic B-spline collocation method (QBCM) and sinc-collocation method using Linsolve Package (SMLP).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Gurtin, M.E., Pipkin, A.C.: A general theory of heat conduction with finite wave speed. Arch. Ration. Mech. Anal. 31, 113–126 (1968)
Miller, R.K.: An integro-differential equation for rigid heat conductors with memory. J. Math. Anal. Appl. 66, 313–332 (1978)
Lodge, A.S., Renardy, M., Nohel, J.A.: Viscoelasticity and rheology. Academic Press, New York (1985)
Ortega, J.M., Davis, S.H., Rosemblat, S., Kath, W.L.: Bifurcation with memory. SIAM J. Appl. Math. 46, 171–188 (1986)
Chen, C., Thome, V., Wahlbin, L.: Finite element approximation of a parabolic integro-differential equation with a weakly singular kernel. Math. Comput. 58, 587–602 (1992)
Tang, T.: A finite difference scheme for partial integro-differential equations with a weakly singular kernel. Appl. Numer. Math. 11(4), 309–319 (1993)
Dehghan, M.: Solution of a partial integro-differential equation arising from viscoelasticity. Int. J. Comp. Math. 83(1), 123–129 (2006)
Zarebnia, M.: Sinc numerical solution for the Volterra integro-differential equation. Comm. Nonlinear Sci. Num. Simul. 15(3), 700–706 (2010)
Fakhar-Izadi, F., Dehghan, M.: The spectral methods for parabolic Volterra integro-differential equations. J. Comput. Appl. Math. 235(14), 4032–4046 (2011)
Long, W.T., Xu, D., Zeng, X.Y.: Quasi wavelet based numerical method for a class of partial integro-differential equation. Appl. Math. Comput. 218, 11842–11850 (2012)
Yang, X., Xu, D., Zhang, H.: Crank-Nicolson/quasi-wavelets method for solving fourth order partial integro-differential equation with a weakly singular kernel. J. Comput. Phys. 234, 317–329 (2013)
Zhang, H., Han, X., Yang, X.: Quintic B-spline collocation method for fourth order partial integro-differential equations with a weakly singular kernel. Appl. Math. Comput. 219, 6565–6575 (2013)
Ali, A., Ahmad, S., Shah, S.I.A., Haq, F.I.: A quartic B-spline collocation technique for the solution of partial integro-differential equations with a weakly singular kernel. Sci. Int. 27(5), 3971–3976 (2015)
Ahmad, S., Ali, A., Shah, S.I.A., Haq, F.I.: A computational algorithm for the solution of second order partial integro-differential equations with a weakly singular kernel using quintic B-spline collocation method. SURJ. 47(4), 709–712 (2015)
Ali, A., Ahmad, S., Shah, S.I.A.: Fazal-i-Haq: A computational technique for the solution of parabolic type integro-differential equation with a weakly singular kernel. SURJ. 48(1), 71–74 (2016)
Fahim, A., Araghi, M.A.F., Rashidinia, J., Jalalvand, M.: Numerical solution of Volterra partial integro-differential equations based on sinc-collocation method. Adv. Dif. Equ. 2017, 362 (2017)
Aziz, I., Khan, I.: Numerical Solution of Partial Integrodifferential Equations of Diffusion Type. Math. Prob. Eng. 2017, 11 (2017). Article ID 2853679
Abbas, M., Majid, A.A., Ismail, AIMd, Rashid, A.: The application of cubic trigonometric B-spline to the numerical solution of the hyperbolic problems. Appl. Math. Comput. 239, 74–88 (2014)
Zin, S.M., Majid, A.A., Ismail, AIMd, Abbas, M.: Cubic trigonometric B-spline approach to numerical solution of wave equation. Int. J. Math. Comput. Sci. 8(10), 1302–1306 (2014)
Abbas, M., Majid, A.A., Ismail, AIMd, Rashid, A.: Numerical method using cubic trigonometric B-Spline technique for nonclassical diffusion problems. Abstract Appl. Anal. 2014, 11 (2014). Article ID 849682
Nazir, T., Abbas, M., Yaseen, M.: Numerical solution of second-order hyperbolic telegraph equation via new cubic trigonometric B-splines approach. Cogent Math. 4, 1382061 (2015)
Heilat, A.S., Ismail, AIMd: Hybrid cubic b-spline method for solving Non-linear two-point boundary value problems. Int. J. Pure Appl. Math. 110(2), 369–381 (2016)
Hashmi, M.S., Awais, M., Waheed, A., Ali, Q.: Numerical treatment of Hunter Saxton equation using cubic trigonometric B-spline collocation method. AIP Adv. 7, 095124 (2017). https://doi.org/10.1063/1.4996740
Yaseen, M., Abbas, M., Nazir, T., Bale, D.: A finite difference scheme based on cubic trigonometric B-splines for a time fractional diffusion-wave equation. Adv. Differ. Equ. 2017, 274 (2017)
Dag, I., Hepson, O.E., Kaçmaz, O.: The trigonometric cubic B-spline algorithm for burgers’ equation. Int. J. Nonlin. Sci. 24(2), 120–128 (2017)
Arora, G., Joshi, V.: A computational approach using modified trigonometric cubic B-spline for numerical solution of Burgers’ equation in one and two dimensions. Alex. Eng. J. 7(2), 1087–1098 (2018)
Tamsir, M., Dhiman, N., Srivastava, V.K.: Cubic trigonometric B-spline differential quadrature method for numerical treatment of Fisher’s reaction-diffusion equations. Alex. Eng. J. 7(3), 2019–2026 (2018)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Ali, A., Khan, K., Haq, F., Shah, S.I.A. (2019). A Computational Modeling Based on Trigonometric Cubic B-Spline Functions for the Approximate Solution of a Second Order Partial Integro-Differential Equation. In: Rocha, Á., Adeli, H., Reis, L., Costanzo, S. (eds) New Knowledge in Information Systems and Technologies. WorldCIST'19 2019. Advances in Intelligent Systems and Computing, vol 930. Springer, Cham. https://doi.org/10.1007/978-3-030-16181-1_79
Download citation
DOI: https://doi.org/10.1007/978-3-030-16181-1_79
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-16180-4
Online ISBN: 978-3-030-16181-1
eBook Packages: Intelligent Technologies and RoboticsIntelligent Technologies and Robotics (R0)