Abstract
Typical Web 2.0 applications are built on abstractions, allowing developers to rapidly and securely develop new features. For decentralised applications, these abstractions are often poor or non-existent.
By proposing a set of abstract but generic building blocks for the development of peer-to-peer (decentralised), private online social networks, we aim to ease the development of user-facing applications. Additionally, an abstract programming system decouples the application from the data model, allowing to alter the front-end independently from the back-end.
The proposed proof-of-concept protocol is based on existing cryptographic building blocks, and its viability is assessed in terms of performance.
You have full access to this open access chapter, Download chapter PDF
Similar content being viewed by others
Keywords
1 Introduction
Privacy on online social media comes in two forms. Platforms generally give plenty of privacy control to platform users, in form of social privacy: users can control which friends can access what content. Recently, the Cambridge Analytica scandal [11] proved again the lack of institutional privacy: while users can choose with whom of their social connections they share data, the host or institute that takes care of the platform usually has unlimited access to personal data. Privacy enhancing tool (PETs) are developed to counter several privacy issues by technological means.
One category of PETs are privacy-preserving databases, where the database of a service itself takes a responsibility on the data it exchanges. This often relates to P3P, which is a web standard that encodes a service’s privacy practices in a machine readable way [22]. An overview of privacy-preserving databases is given in Sect. 3.1.
Another often encountered paradigm in these PETs is moving data away from a central host or institution: decentralisation of services is believed to enhance institutional privacy for its end-users, since the institution itself is taken out of the picture. Several efforts have been made, both academical and community projects, to “re-decentralise” the internet, or parts thereof. In Sect. 3, we enumerate some notable projects that attempt to decentralise online social media.
We argue that at least one problem in this “re-decentralisation” is the lack of abstractions for developers. Where in typical centralised systems developers have tools like SQL (often in combination with object relational mapping (ORM)), or cookies (often as part of an authentication system), decentralised systems are often built “from scratch”, drafting protocols (or extensions thereof) on a per-feature basis.
As an additional consequence, the coupling of the front-end application and the back-end decentralised networking components make it difficult to migrate data, or to fix a security issue in the back-end in a consistent, forward-compatible way.
In Sect. 4 we propose a proof-of-concept protocol for authenticated, confidential data exchange in a peer-to-peer network. This protocol should allow a participant to share with their friends, and stay anonymous for the rest of the network; it offers a form of cryptographically mandatory access control on the data. Since it is based on a peer-to-peer overlay network and therefore has no central processing infrastructure, the system should be lightweight enough to run on constrained devices like smartphones. We evaluate the performance characteristics in Sect. 5.
2 Problem Statement
Many protocols on the internet are federated; examples including email or XMPP. In case of email, Mailchimp (a large email marketing company) notes in 2015 that more than 70 % of their email targets Google’s gmail.com domain. Their statistics exclude the “foreign” domains hosted on Google’s and Microsoft’s mail servers, which suggests an even larger market share [13]. Other online resources suggest that both Microsoft and GMail are by far the world most popular email service providers [9, 18]. This illustrates that federated networks may still lead to centralisation, defeating the decentralisation and privacy-related benefitsFootnote 1 [17].
The case of email illustrates another drawback of federated systems: the user has to pick a provider. A quick survey on Google, Bing and DuckDuckGo results in mail.com and gmail.com as top two results, with Microsoft’s live.com usually third for the keywords “create email account”.
Another prime example of an attempt at decentralising authentication is OpenID, an open standard and authentication protocol. In practice, users employ a large OpenID provider (often Google or Microsoft), which effectively centralises login history with a few providers.
In the Web 2.0 paradigm, developers employ certain tools (abstractions, SDKs, libraries) that aid the development of their applications. For example, SQL (with optional ORM or query builder) is used to store and retrieve data. “Asynchronous Javascript and XML (AJAX)” is used for dynamically changing retrieving information. Cookies (with for example OAuth) are used for authentication and (re-)identification. Similar abstractions can be identified in the mobile app paradigm, building applications for Android or similar.
For decentralised applications, these abstractions are often non-existent, too domain-specific (e.g. Pandora has objects like “Person”, “City”), or too low-level: PeerSoN [7] uses files, while RetroShare’s GXS [28] uses “groups” containing “messages” as basic building blocks.
The remainder of this paper is concerned with the development of an abstract data model and platform, meant to be at the basis of a peer-to-peer online social network (OSN). It should be portable and efficient enough to run on smartphones, and it should provide a minimum of access-control. These properties fit our interpretation of the privacy definition of Agre and Rotenberg: “The freedom from unreasonable constraints on the construction of one’s own identity” [2]. OSNs are important in human social communication; they should facilitate social interaction, and their use and development should not be obstructed by technical difficulties.
3 Related Work
Troncoso et al. have enumerated different properties of decentralised systems. A system can be called decentralised, while in fact certain aspects are still inherently or partially centralised, e.g. trackers and supernodes in BitTorrent or Tor’s Directory Authorities [30].
3.1 Privacy-Preserving Databases
The field of privacy-preserving databases is concerned with storing, processing, and releasing data while preserving data. Different database management system (DBMS) have different properties regarding privacy preservation.
Often cited is Platform for Privacy Preferences Project (P3P), a web-based protocol that enables websites to communicate their privacy practices to the browser. The browser interprets and represents this information, and can automatically make decisions based on user preferences [22]. Research is being carried out to develop DBMS that are able to enforce promises encoded in languages such as P3P [5];
Another research area is the development DBMS that allow queries over encrypted data. These systems are typically cloud- or infrastructure-based, as opposed to peer-to-peer. As an example, Cao et al. developed a graph database that supports queries over its encrypted data [8].
3.2 Private Online Social Networks
Efforts for building a decentralised online social network are almost commonplace, with for example Diaspora*, Mastodon, and SecuShare. One notable community project is RetroShare, which is a so-called friend-to-friend networkFootnote 2 providing file-sharing, fora and other services. In October 2017, Soler published the Generic data eXchange System (GXS) [28], on which they ported RetroShare’s fora and newsgroups. The goal of GXS is to make development of new features easier, by providing an abstract layer for developers.
One academic decentralised online social network is called PeerSoN [7]. PeerSoN uses a distributed hash table (DHT) to localise files on a decentralised network. Writing to and reading from those files is subject to mandatory access control (MAC), implemented using cryptography.
A commercial example is MaidSAFE, who are developing a distributed filesystem [12], supported by cryptographic currency [14] based on supernodes.
3.3 Cryptographic Building Blocks
Where centralised applications can rely on the infrastructure granting or denying access, a peer-to-peer system has to rely on cryptography and key management. After all, when data passes through or is stored on unknown or untrusted peers, they should not be able to read it.
The cryptographic currency Monero takes this principle to the extreme: their protocol attempts to hide the sender, receiver and amount of a transaction, while still solving the double-spend problem [25]. Monero relies on a few existing cryptographic building blocks to reach their goal, two of which are at the basis of Glycos.
To conceal the sender, Monero uses ring signatures [24]. This allows the real sender to hide himself among a list of potential senders. Additionally, they anonymise the receiver by computing a related but unlinkable receiver key. We use a variant of both schemes in Sect. 4.5, with similar purposes.
4 Solution Design
For both centralised and decentralised applications, providing the developer with abstractions has several benefits. Applications are faster, easier and more secure to develop and to maintain, and the developer does not need knowledge of the underlying systems.
We propose a building block for distributed and private data storage, the equivalent of a DBMS in the classical paradigms, based on graph databases.
4.1 Privacy by Fine-Grained Access Control
Porting privacy definitions to a peer-to-peer setting is anything but trivial, and requires deeper research on its own. An illustration: legislation like the GDPR [23] is concerned with processors and controllers, which both are typically depicted by legal entities that process or control personal data. In a peer-to-peer setting, where the central authority and institution is taken out of the picture, it becomes difficult to clearly point out who is processor or controller: they all depend on the specifics of the considered peer-to-peer system.
In an overlay network like the one presented, one could say the whole network becomes the hosting institution. Institutional privacy thus means privacy with respect to the network’s peers.
When we consider the institution as an eavesdropper, some of the properties we want to achieve are:
- confidentiality. :
-
The overlay network should not learn the semantic meaning of the data it stores.
- control. :
-
The end-user should control the data he stores on the overlay network.
- unlinkability. :
-
The overlay network cannot sufficiently distinguish whether two items of interest are related or not [21].
By storing data in a granular way as edges and vertices, and anonymising every data point, we can ensure unlinkability. We will employ well-established cryptographic building blocks to anonymise data, encrypt data, and provide access control.
4.2 Access Controlled Graph Database
A graph database is a database of triplets \((s,p,o)\); a subject \(s\), predicate \(p\), and object \(o\). A triplet \((s,p,o)\) represents the directed edge with label \(p\), from \(s\) to \(o\).
We construct a query system wherein vertices and edges are efficiently searchable and traversable for authorised users, while being encrypted, and thus unintelligible for unauthorised users. Data is stored on a DHT based on Kademlia [19]. All vertices have an owner and an (optionally empty) access control list; the owner of a vertex can optionally grant others the right to append additional edges to specific vertices. In Fig. 1, Alice has granted Bob the right to post on her wall.
For this paper, we assume a network of trust; users have access to (correct) key information of their peers. Trust models used in PETs include trust-on-first-use (e.g. Signal) and offline key exchange (PGP, OTR).
4.3 Data Model
In a conventional graph database, information does not have access rights; we thus propose a simpleFootnote 3 access control model that extends an RDF-based model [16]. By splitting up the concept of vertices and edges into two separate objects, it is possible to alter a vertex’ content independently from the edge list, and vice versa. It also allows us to add security-related information to both objects.
A vertex \(s\) is identified by its owner, and contains an access control list enumerating users that can create edges with \(s\) as subject. This allows for typical OSN features like a personal “wall”, where Alice’s friends can leave posts to be read for her and her friends. Those posts in turn can then contain a comments section, to allow for more interaction.
4.4 Notational Conventions
Since we will be using a few cryptographic concepts, it is necessary to define some notation. The public key system used throughout the design is Curve25519 [4]. Public keys are points on an elliptic curve, and their discrete logarithms are the respective private keys. When \(\ell \) is the size of the underlying field, \(r\leftarrow [0, \ell - 1]\) picks a field element uniformly at random. We will assume a known long term public key  with corresponding private key
with corresponding private key  for every participant \(i\). Identification can happen in a face-to-face meeting: we assume that two persons that want to use the network together have access to correct key information of each other.
for every participant \(i\). Identification can happen in a face-to-face meeting: we assume that two persons that want to use the network together have access to correct key information of each other.
\(\mathcal {H}\) is a cryptographically secure hash function (the Keccak-based [6] SHA 3-256 function), and \(\mathcal {H}_s\) is a hash function onto the underlying field of the elliptic curve.
4.5 Implementation
We will store every vertex \(s\) of the graph database as an object in a Kademlia-based [19] DHT, storing vertices that have \(s\) as subject alongside \(s\) for easy graph traversal. The DHT thus understands two kinds of put operations; one for vertices and one for edges, while the get operation returns both the vertex and the associated edges.
Note that since vertices are identified by their owner, we cannot use the long term  public key. Instead, inspired on ByteCoin’s “Stealth Addresses” [29, 31] and Monero’s “one-time addresses” [25], we derive a random key from the long term key
public key. Instead, inspired on ByteCoin’s “Stealth Addresses” [29, 31] and Monero’s “one-time addresses” [25], we derive a random key from the long term key  :
:
Algorithm 1 (Generate an ephemeral public key)
Given the public key  of Alice, Bob generates an ephemeral (one-time) public key for Alice as follows:
of Alice, Bob generates an ephemeral (one-time) public key for Alice as follows:

This key clearly belongs to Alice: only Alice knows the integer \(a\) required to construct her secret key. She can recognise that this key belongs to her by checking whether \(A'\) equals \(pk^\text {alice}_\text {OT}\) in
Due to this property, we will call \(R\) the “recogniser”. Note that the serialisation of the ephemeral public key together with the recogniser only takes the size of two points (\(R\) and  ), which is 64 bytes when using Curve25519 [4]. Since \(r\) is only used in the key derivation, it is a temporary variable. Note that \(\mathcal {H}_s(rA) = \mathcal {H}_s(aR)\) is an elliptic-curve Diffie-Hellman key agreement [10, 20] with a random key \(R=rG\).
), which is 64 bytes when using Curve25519 [4]. Since \(r\) is only used in the key derivation, it is a temporary variable. Note that \(\mathcal {H}_s(rA) = \mathcal {H}_s(aR)\) is an elliptic-curve Diffie-Hellman key agreement [10, 20] with a random key \(R=rG\).
The ephemeral public key  is indistinguishable from random. Formally, the probability distributions of
is indistinguishable from random. Formally, the probability distributions of  and \((R=rG, A=aG, C=cG)\) are computationally indistinguishable for \(r,a,c\) chosen randomly and uniformly from \([0,\ell -1]\).
and \((R=rG, A=aG, C=cG)\) are computationally indistinguishable for \(r,a,c\) chosen randomly and uniformly from \([0,\ell -1]\).
Proof
Assume we can distinguish  and \((R\,=\,rG, A\,=\,aG, C\,=\,cG)\) using some distinguisher \(\mathcal {A}\). This means we can solve the decisional Diffie-Hellman problem: to distinguish \((R, A, K\,=\,rA\,=\,aR)\) and \((R, A, C)\), it suffices to run \(\mathcal {A}\) on \((R, A, \mathcal {H}_s(K)G + A)\) and \((R, A, C)\). \(\square \)
and \((R\,=\,rG, A\,=\,aG, C\,=\,cG)\) using some distinguisher \(\mathcal {A}\). This means we can solve the decisional Diffie-Hellman problem: to distinguish \((R, A, K\,=\,rA\,=\,aR)\) and \((R, A, C)\), it suffices to run \(\mathcal {A}\) on \((R, A, \mathcal {H}_s(K)G + A)\) and \((R, A, C)\). \(\square \)
We can now define a vertex.
Definition 1 (vertex)
A vertex \(V\) is a 7-tuple \((O,R,ACL,R_{ACL},v,c,S)\).
The key \(O\) is an ephemeral, unique public key derived from the private key held by the owner of this vertex, the owner key. The point \(R\) is the recogniser used to generate key \(O\). The list \(ACL\) is the access control list, listing all ephemeral public keys that are allowed to link other vertices from this vertex using edges. The point \(R_{ACL}\) is the recogniser used to generate all ephemeral public keys in \(ACL\). Optionally, \(v\) is the encrypted associated value or content of the vertex. The clock \(c\) is a positive integer to keep track of the vertex version. The Schnorr signature \(S\) is a \(\mathcal {BNN-IBS}\) signature [3, 26, 27] of \((R,ACL,R_{ACL},v,c)\) generated using \(O\).
In this definition, the access control list \(ACL\) contains ephemeral public keys generated with a common \(r\), thus having the common recogniser \(R_{ACL}=rG\). This operation effectively anonymises vertex appends, while the assigned users can still recognise (using \(R_{ACL}\)) their eligibility to create edges.
By using Algorithm 1 to generate \(O\) and the keys in \(ACL\), these public keys are indistinguishable from random and thus unlinkable to their owners.
There is still one problem to overcome: imagine we use the above (Schnorr) signature to sign an edge. The signer is always identifiable, and Eve—the eavesdropper—could distinguish edges based on their associated signer. Eve should only learn about the validity of the edge. In “How to leak a secret” [24] Rivest, Shamir, and Tauman describe an elegant concept and method to overcome this issue. They propose a so-called “ring-signature”, a signature which proves knowledge of one secret key of a set, without revealing which.
A ring-signature scheme based on elliptic curves is documented by Abe, Ohkubo, and Suzuki [1, Appendix A].
Algorithm 2 (Generate ring signature)
A signer with secret key \(x_k\) signs message \(m\) with public-key list \(\mathcal {R}_s = {Y_0, Y_1, \dots , Y_{n-1}}\)
-
1.
Select \(\alpha ,c_i\leftarrow [0,\ell -1]\) for \(i=0,\dots ,n-1,i\ne k\), and compute \(z=\alpha G + \sum _{i=0,i\ne k}^{n-1}c_i Y_i\)
-
2.
Compute
$$\begin{aligned} c&=\mathcal {H}_s(\mathcal {R}_s||m||z)\\ c_k&=c-\sum _{i=0,i\ne k}^{n-1}c_i \mod q\\ s&= \alpha - c_k x_k \mod q \end{aligned}$$ -
3.
Return \(\sigma =(s,c_0,\dots ,c_{n-1})\)
Algorithm 3 (Verify ring signature)
A verifier verifies signature \(\sigma \). \((L,m,\sigma )\) by checking whether
An edge can now be defined as an object with an encrypted value, pointing from a subject to an object, with the value and identifier of the object being encrypted:
Definition 2 (edge)
An edge \(E\) between two vertices \(V_s=(O_s,R_s,ACL_s,R_{ACL,s},v_s,c_s,S_s)\) (the subject) and \(V_o=(O_o,R_o,ACL_o,R_{ACL,o},v_o,c_o,S_o)\) (the object) is a 5-tuple
The ring \(\mathcal {R}_s=\{O_1, O_2, \dots , O_i = O_s, \dots , O_n\}\) is a set of public keys containing all \(n\) public keys in \(ACL_s\). For every key in \(ACL_s\), \(ACL_E\) contains the encrypted key \(k\). It is encrypted \(n\) times using a standard hybrid encryption, based on a Diffie-Hellman exchange with the random point \(K_{ACL}\) using the symmetric cipher \(\mathcal {E}\). \(l\) is the label of the edge. \(S\) is a ring signature [1, Appendix A] over the ring \(\mathcal {R}_s\) of \((O_s,ACL_E,\mathcal {E}_k(l||O_s))\). The label and object are encrypted using the same symmetric cipher \(\mathcal {E}\) with key \(k\).
The two main components implemented are the middleware for the cryptographic graph, and the custom Kademlia router. The Kademlia router is responsible for connection with other peers, storing and retrieving encrypted graph data on the network. The graph API implements the encryption and decryption of the graph, feeding it from and back to the application.

5 Performance Evaluation
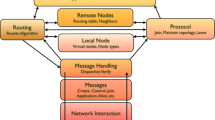
To validate the technical viability, we have built a demonstrator implementation in RustFootnote 4. We call this demonstrator Glycos, and serves as a middleware providing an interface for traversing the graph with an asynchronous API. It contains the necessary networking and cryptographic components to query the network for, and to create and store vertices and edges. For a graphical overview, refer to Figs. 2 and 3.
Additionally, it contains an object relational mapping ORM interface that maps objects to vertices and edges and vice versa. This allows a developer to think in terms of objects and their relations, like is common when working with relational databases. The ORM-interface contains generated bindings to Java, to demonstrate the viability on the Android platform. Listing 1 contains example code verified testing on both a virtual and a physical Android device.
Since practicality and performance are key in the design, a thorough analysis of both aspects is mandatory. Note that a vertex can be serialised in \(156+|v|+32|ACL|\) bytes when taking a 64-bit integer for the clock value. We saved \(32\) bytes by using the \(\mathcal {BNN-IBS}\) Schnorr signature [3] scheme, which allows us to omit the owner key from the serialisation.
When an edge \(E\) is transmitted together with its accompanying vertex, we can omit the subject \(O_s\) and the ring \(\mathcal {R}_s\) from \(E\)s serialisation. This allows a serialisation in \(112+|l|+80|R_s|\) bytes.
The maximum transmission unit (MTU) for Ethernet is about 1500 bytes, so for a small (\(<15\)) amount of participants both a vertex or an edge could fit a single Ethernet frame. At 1500 bytes, one megabyte can store around 700 vertices or edges, one gigabyte around 700 000. Since modern smartphones and computers come with plenty of storage, often exceeding 8 GB, this is ought to be compact enough (Table 1).
We ran a few benchmarks to measure how fast vertices and edges can be generated and decrypted. Timings correspond to a at least few hundreds of encryptions and decryptions per second. Note that at the time of writing, the ARM based smartphone platform takes no advantage of the available NEON instruction setFootnote 5 nor from the 64 bit instructions. In other words, the ARM build has still room for optimisation. All notable benchmarks are represented in Table 2.
6 Conclusion
Decentralisation of a service is believed to lead to more privacy. We noted that today’s decentralised online social network (OSNs) come in two forms: at one hand there are federated OSNs, and at the other there are peer-to-peer OSNs. Federated networks have as disadvantage that the end-user has to choose a provider or “pod”, which in the case of e-mail has lead to re-centralisation of users’ data.
Most peer-to-peer networks reinvent the wheel: often on a per-feature basis, these systems mainly design a private and secure protocol. This is in contrast with centralised services, where developers employ abstractions like SQL, ORM, and cookies to build applications, often without having to consider cryptography.
An abstract data model can help to overcome this unbalance. While existing data models such as GXS [28] have also observed this unbalance, proposed solutions are often still application specific. We propose a simple graph database-like service built upon Kademlia, on which application developers can store and query arbitrary data. This data model is encrypted and authenticated and thus only readable and writeable by users with the necessary permissions. Moreover, it has been made relatively easy to use through the ORM layer, and shown to be efficient enough to run on mobile devices.
7 Future Work
In the current model, efficient update and delete operations are still lacking, due to the risk of replay attacks. By introducing a notion of time, or more precisely the notion of happened-before [15], these attacks can be countered, and efficient deletion could be implemented. These are important considerations, since these features would increase the user’s control over their data.
As touched upon in Sect. 4.1, privacy properties and definitions are not well studied in a peer-to-peer context. Formally identifying adversaries and their capabilities in a peer-to-peer OSN, and making provable definitions about them can increase confidence in these applications.
Looking at Glycos as a middleware, future research should further enhance the platform in itself, making it more practical to build actual applications and to make peer-to-peer overlay systems simpler to develop.
Notes
- 1.
In case of email, it is enough that just one participant in a conversation should be on a malicious server to compromise all communication. PETs such as PGP try to overcome this issue.
- 2.
Troncoso et al. refer to this as “P2P: Nodes Assist Other Nodes” [30].
- 3.
This model is “simple” in the sense that more complex models are possible, and may be interesting for future research: co-ownership, write-only, or read-only rights can all have useful applications.
- 4.
“Rust is a systems programming language that runs blazingly fast, prevents segfaults, and guarantees thread safety.” https://www.rust-lang.org/.
- 5.
NEON support is on the roadmap for curve25519-dalek; cfr. https://github.com/dalek-cryptography/curve25519-dalek/issues/147.
References
Abe, M., Ohkubo, M., Suzuki, K.: 1-out-of-n signatures from a variety of keys. In: Zheng, Y. (ed.) ASIACRYPT 2002. LNCS, vol. 2501, pp. 415–432. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-36178-2_26
Agre, P.E., Rotenberg, M.: Technology and Privacy: The New Landscape. MIT Press, Cambridge (1998)
Bellare, M., Namprempre, C., Neven, G.: Security proofs for identity-based identification and signature schemes. J. Cryptol. 22(1), 1–61 (2009)
Bernstein, D.J.: Curve25519: new Diffie-Hellman speed records. In: Yung, M., Dodis, Y., Kiayias, A., Malkin, T. (eds.) PKC 2006. LNCS, vol. 3958, pp. 207–228. Springer, Heidelberg (2006). https://doi.org/10.1007/11745853_14. ISBN 978-3-540-33852-9
Bertino, E., Byun, J.-W., Li, N.: Privacy-preserving database systems. In: Aldini, A., Gorrieri, R., Martinelli, F. (eds.) FOSAD 2004-2005. LNCS, vol. 3655, pp. 178–206. Springer, Heidelberg (2005). https://doi.org/10.1007/11554578_6
Bertoni, G., et al.: Keccak sponge function family main document. In: Submission to NIST (Round 2), vol. 3, p. 30 (2009)
Buchegger, S., et al.: PeerSoN: P2P social networking - early experiences and insights. In: Proceedings of the Second ACM Workshop on Social Network Systems Social Network Systems 2009, co-located with Eurosys 2009, Nüurnberg, Germany, March 2009, pp. 46–52 (2009)
Cao, N., et al.: Privacy-preserving query over encrypted graph-structured data in cloud computing. In: 2011 31st International Conference on Distributed Computing Systems (ICDCS), pp. 393–402. IEEE (2011)
Datanyze: Email Hosting Market Share Report. Datanyze, 12 June 2018. https://www.datanyze.com/market-share/email-hosting. Accessed 14 June 2018
Diffie, W., Hellman, M.: New directions in cryptography. IEEE Trans. Inf. Theory 22(6), 644–654 (1976)
Graham-Harrison, E., Cadwalladr, C.: Revealed: 50 million Facebook profiles harvested for Cambridge Analytica in major data breach. In: The Guardian, March 2018. https://www.theguardian.com/news/2018/mar/17/cambridge-analytica-facebook-influence-us-election
Irvine, D.: MaidSafe Distributed File System. Technical report (2010)
Khan, O.: Major email provider trends in 2015: Gmail’s Lead in- creases. Mailchimp, 15 July 2015. https://blog.mailchimp.com/major-email-provider-trends-in-2015-gmail-takes-a-really-big-lead/
Lambert, N., Ma, Q., Irvine, D.: The Decentralised Network Token. Technical report MaidSafe, Technical report, Safecoin (2015)
Lamport, L.: Time, clocks and the ordering of events in a distributed system. Commun. ACM 21(7), 558–565 (1978)
Lassila, O., Swick, R.R.: Resource Description Framework (RDF): Model and Syntax. W3C Recommendation. W3C (1997). https://www.w3.org/TR/WD-rdf-syntax-971002/. Accessed 20 Oct 2017
Lewis, S.J.: On emergent centralization (2018). https://fieldnotes.resistant.tech/defensive-decentralization/. Accessed 31 Oct 2018
Lewkowicz, K.: Here’s What We Learned After Tracking 17 Billion Email Opens [Infographic], 21 March 2017. https://litmus.com/blog/2016-email-client-market-share-infographic. Accessed 14 June 2018
Maymounkov, P., Mazières, D.: Kademlia: a peer-to-peer information system based on the XOR metric. In: Druschel, P., Kaashoek, F., Rowstron, A. (eds.) IPTPS 2002. LNCS, vol. 2429, pp. 53–65. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45748-8_5
Miller, V.S.: Use of elliptic curves in cryptography. In: Williams, H.C. (ed.) CRYPTO 1985. LNCS, vol. 218, pp. 417–426. Springer, Heidelberg (1986). https://doi.org/10.1007/3-540-39799-X_31
Pfitzmann, A., Hansen, M.: A terminology for talking about privacy by data minimization: anonymity, unlinkability, undetectability, unobservability, pseudonymity, and identity management (2010)
Platform for Privacy Preferences (P3P) Project. W3C Recommendation. W3C, February 2014. https://www.w3.org/P3P/. Accessed 31 Oct 2018
Regulation (EU) 2016/679 of the European Parliament and of the Council of 27 April 2016 on the protection of natural persons with regard to the processing of personal data and on the free movement of such data, and repealing Directive 95/46/EC (General Data Protection Regulation), 27 April 2016
Rivest, R.L., Shamir, A., Tauman, Y.: How to leak a secret. In: Boyd, C. (ed.) ASIACRYPT 2001. LNCS, vol. 2248, pp. 552–565. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45682-1_32
Van Saberhagen, N.: Cryptonote v2.0 (2013)
Schnorr, C.-P.: Efficient signature generation by smart cards. J. Cryptol. 4(3), 161–174 (1991)
Schnorr, C.-P.: Method for identifying subscribers and for generating and verifying electronic signatures in a data exchange system. U.S. pat. 4995082, February 1991
Soler, C.: A Generic Data Exchange System for Friend-to-Friend Net- works. Technical report, INRIA Grenoble-Rhone-Alpes (2017)
Todd, P.: [bitcoin-development] Stealth addresses (2014). https://www.mail-archive.com/bitcoin-development@lists.sourceforge.net/msg03613.html. Accessed 12 Feb 2017
Troncoso, C., et al.: Systematizing decentralization and privacy: lessons from 15 years of research and deployments. In: Proceedings on Privacy Enhancing Technologies, vol. 2017, no. 4, pp. 404–426 (2017)
user ‘bytecoin’. Untraceable transactions which can contain a secure message are inevitable (2011). https://bitcointalk.org/index.php?topic=5965.0. Accessed 12 Feb 2017
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 IFIP International Federation for Information Processing
About this chapter
Cite this chapter
De Smet, R., Dooms, A., Braeken, A., Pierson, J. (2019). Glycos: The Basis for a Peer-to-Peer, Private Online Social Network. In: Kosta, E., Pierson, J., Slamanig, D., Fischer-Hübner, S., Krenn, S. (eds) Privacy and Identity Management. Fairness, Accountability, and Transparency in the Age of Big Data. Privacy and Identity 2018. IFIP Advances in Information and Communication Technology(), vol 547. Springer, Cham. https://doi.org/10.1007/978-3-030-16744-8_9
Download citation
DOI: https://doi.org/10.1007/978-3-030-16744-8_9
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-16743-1
Online ISBN: 978-3-030-16744-8
eBook Packages: Computer ScienceComputer Science (R0)





 ). The definition of those access rights are contained within every vertex.
). The definition of those access rights are contained within every vertex.

