Skip to main content
Springer Nature Link
Log in

Outage Probability Analysis for Hybrid Satellite and Terrestrial Network with Different Combining Schemes

  • Conference paper
  • First Online:
Wireless and Satellite Systems (WiSATS 2019)

Included in the following conference series:

  • 1201 Accesses

Abstract

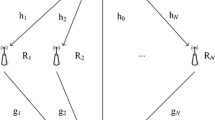
In this paper, we investigate the outage probability (OP) of a hybrid satellite and terrestrial cooperative network (HSTCN) with the terrestrial relay having multiple antennas. Here, it is assumed that the satellite channel undergoes the shadowed-Rician fading, while terrestrial channel follows correlated Rayleigh fading. By supposing that statistic channel state information (CSI) of relay-destination link is available at the relay, we first obtain the end-to-end output signal-to-noise ratio (SNR) expression of the HSTCN. Then, the closed-form expressions of the outage probability for the considered system are derived, where two combining schemes, namely, selection combing (SC) and maximal-ratio combining (MRC) protocols are utilized at the destination to combine signals form the satellite and relay. Finally, numerical results are given to validity of the OP analysis, and reveal the performance difference of the two combining schemes.

Supported in part by the Key International Cooperation Research Project under Grant 61720106003, in part by National Natural Science Foundation of China under Grant 61801234 and 61271255.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution

Subscribe and save

Springer+ Basic
$34.99 /Month
  • Get 10 units per month
  • Download Article/Chapter or eBook
  • 1 Unit = 1 Article or 1 Chapter
  • Cancel anytime
Subscribe now

Buy Now

Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Similar content being viewed by others

References

  1. Lin, M., Lin, Z., et al.: Joint beamforming for secure communication in cognitive satellite terrestrial networks. IEEE J. Sel. Areas Commun. 36(5), 1017–1029 (2018)

    Article  Google Scholar 

  2. Paolo, C., Giovanni, G., Sastri, K.: A survey on mobile satellite systems. Int. J. Satellite Commun. Netw. 28(1), 29–57 (2010)

    Google Scholar 

  3. Bhatnagar, M.R., Arti, M.K.: Performance analysis of AF based hybrid satellite-terrestrial cooperative network over generalized fading channels. IEEE Commun. Lett. 17(10), 1912–1915 (2013)

    Article  Google Scholar 

  4. Huang, Q., Lin, M., An, K., Ouyang, J., Zhu, W.: Secrecy performance of hybrid satellite-terrestrial relay networks in the presence of multiple eavesdroppers. IET Commun. 12(1), 26–34 (2018)

    Article  Google Scholar 

  5. An, K., Lin, M., Liang, T., et al.: Performance analysis of multi-antenna hybrid satellite-terrestrial relay networks in the presence of interference. IEEE Trans. Commun. 63(11), 4390–4404 (2015)

    Article  Google Scholar 

  6. Zhao, Y., Chen, H., Xie, L., Wang, K.: Exact and asymptotic ergodic capacity analysis of the hybrid satellite-terrestrial cooperative system over generalised fading channels. IET Commun. 12(11), 1342–1350 (2018)

    Article  Google Scholar 

  7. Lin, Z., Lin, M., et al.: Robust secure beamforming for 5G cellular networks coexisting with satellite networks. IEEE J. Sel. Areas Commun. 36(4), 932–945 (2018)

    Article  Google Scholar 

  8. Arti, M.K., Bhatnagar, M.R.: Beamforming and combining in hybrid satellite-terrestrial cooperative systems. IEEE Commun. Lett. 18(3), 483–486 (2014)

    Article  Google Scholar 

  9. Sreng, S., Escrig, B., Boucheret, M.L.: Exact symbol error probability of hybrid/integrated satellite-terrestrial cooperative network. IEEE Trans. Wirel. Commun. 12(3), 1310–1319 (2013)

    Article  Google Scholar 

  10. Ju, M.C., Kim, I.M., Dong, I.K.: Joint relay selection and relay ordering for DF-based cooperative relay networks. IEEE Trans. Commun. 60(4), 908–915 (2012)

    Article  Google Scholar 

  11. An, K., Ouyang, J., Lin, M., et al.: Outage analysis of multi-antenna cognitive hybrid satellite-terrestrial relay networks with beamforming. IEEE Commun. Lett. 19(7), 1157–1160 (2015)

    Article  Google Scholar 

  12. Miridakis, N.I., Vergados, D.D., Michalas, A.: Dual-hop communication over a satellite relay and shadowed Rician channels. IEEE Trans. Veh. Technol. 64(9), 4031–4040 (2015)

    Article  Google Scholar 

  13. Abdi, A., Lau, W.C., Alouini, M.S., Kaveh, M.: A new simple model for land mobile satellite channels: first- and second-order statistics. IEEE Trans. Wirel. Commun. 2(3), 519–528 (2003)

    Article  Google Scholar 

  14. Gradshteyn, I.S., Ryzhik, I.M.: Table of Integrals, Series, and Products. Academic Press, San Diego (2010)

    Google Scholar 

  15. Lin, M., Yang, L., Zhu, W.P., et al.: An open-loop adaptive space-time transmit scheme for correlated fading channels. IEEE J. Sel. Topics Sig. Process. 12(2), 147–158 (2008)

    Article  Google Scholar 

  16. Dakdouki, A.S., Tabulo, M.: On the eigenvalue distribution of smart-antenna arrays in wireless communication systems. Antennas Propag. Mag. IEEE 46(4), 158–167 (2004)

    Article  Google Scholar 

  17. Lin, M., Ouyang, J., Zhu, W.P.: Joint beamforming and power control for device-to-device communications underlaying cellular networks. IEEE J. Sel. Areas Commun. 34(1), 138–150 (2016)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. College of Communications Engineering, Army Engineering University of PLA, Nanjing, 210007, China

    Guoqiang Cheng, Zhi Lin & Qingquan Huang

  2. Nanjing Institute of Telecommunication Technology, Nanjing, 210007, China

    Guoqiang Cheng & Min Lin

  3. Key Lab of Broadband Wireless Communication and Sensor Network Technology, Ministry of Education, Nanjing University of Posts and Telecommunications, Nanjing, 210003, China

    Min Lin & Jian Ouyang

Authors
  1. Guoqiang Cheng
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhi Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Min Lin
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Qingquan Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Jian Ouyang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Guoqiang Cheng .

Editor information

Editors and Affiliations

  1. Harbin Institute of Technology, Harbin, China

    Min Jia

  2. Harbin Institute of Technology, Harbin, China

    Qing Guo

  3. Harbin Institute of Technology, Harbin, China

    Weixiao Meng

Rights and permissions

Reprints and permissions

Copyright information

© 2019 ICST Institute for Computer Sciences, Social Informatics and Telecommunications Engineering

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Cheng, G., Lin, Z., Lin, M., Huang, Q., Ouyang, J. (2019). Outage Probability Analysis for Hybrid Satellite and Terrestrial Network with Different Combining Schemes. In: Jia, M., Guo, Q., Meng, W. (eds) Wireless and Satellite Systems. WiSATS 2019. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, vol 281. Springer, Cham. https://doi.org/10.1007/978-3-030-19156-6_45

Download citation

  • DOI: https://doi.org/10.1007/978-3-030-19156-6_45

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-030-19155-9

  • Online ISBN: 978-3-030-19156-6

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics