Abstract
In engineering, design analyses of complex products rely on computer simulated experiments. However, high-fidelity simulations can take significant time to compute. It is impractical to explore design space by only conducting simulations because of time constraints. Hence, surrogate modelling is used to approximate the original simulations. Since simulations are expensive to conduct, generally, the sample size is limited in aerospace engineering applications. This limited sample size, and also non-linearity and high dimensionality of data make it difficult to generate accurate and robust surrogate models. The aim of this paper is to explore the applicability of Random Forests (RF) to construct surrogate models to support design space exploration. RF generates meta-models or ensembles of decision trees, and it is capable of fitting highly non-linear data given quite small samples. To investigate the applicability of RF, this paper presents an approach to construct surrogate models using RF. This approach includes hyperparameter tuning to improve the performance of the RF’s model, to extract design parameters’ importance and if-then rules from the RF’s models for better understanding of design space. To demonstrate the approach using RF, quantitative experiments are conducted with datasets of Turbine Rear Structure use-case from an aerospace industry and results are presented.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Machine learning
- Random Forests
- Hyperparameter tuning
- Surrogate model
- Meta-models
- Engineering design
- Aerospace
1 Introduction
In aerospace industry, engineers develop highly complex composite and metallic engine structures, fan cases and exhaust systems. The early design phase of these components and their performance estimation is a complex multidisciplinary problem, and it involves analyzing the effects of aero performance, mechanical functions and producibility aspects. For this, simulations play a vital role to help to have a better understanding of the functional behaviour and to predict possible failure modes in design concepts. However, high-fidelity simulations can take significant time to compute. Typically, a large system has millions, if not billions of possibilities to explore in the design space [11]. Thus, it is impractical to explore the design space by conducting simulations for all possible design concepts due to the time constraints. Hence, to minimize the number of simulations which is needed to investigate a certain design space, different approaches are used. One of the approaches is surrogate modelling which is also known as response surface modelling and metamodeling [14, 18].
Surrogate models are used to approximate the time-consuming simulations by mimicking the complex behaviour of the underlying simulation model. This provides a great opportunity to explore as many as design concepts without needing more computationally expensive simulations. The generation of surrogate models requires a dataset of inputs and known outputs. Since simulations are expensive to conduct, datasets are usually small in real-world context. The size of the data sets and the complexity of the underlying simulation model make it difficult to generate accurate enough and robust surrogate models. Thus, the challenge is to generate a model as accurate as possible with a small size of datasets for design space exploration. This motivates to study surrogate modelling and methods that can be helpful to construct surrogate models as accurate as possible. For instance, in many studies, the applicability of widely used methods such as Support Vector Machines (SVM), Artificial Neural Networks, Radial Basis Function, Kriging methods, and Linear Regression (LR) have been investigated to construct surrogate models [1, 5, 9, 17, 22].
Furthermore, the performance of two tree methods (Random Forests and M5P) have been investigated for surrogate modelling and concluded that these tree models performed as similar to the widely used methods such as LR and SVM [6]. The authors of this study stated that tree model could provide comprehensibility (if-then rules) that could be used to interpret model behaviour. Though tree models have been suitable and have shown to have a better performance in other applications, they have been rarely used for surrogate modeling in design engineering. Furthermore, Random Forests (RF) generate ensembles of decision trees, and they are capable of fitting highly non-linear data given quite small samples [2, 15]. Therefore, we choose a tree method, RF, to explore its applicability for surrogate modeling. The aim of this paper is to support design space exploration of Turbine Rear Structure (use-case) using RF generated surrogate models. For this, we present an approach that aims (1) to construct surrogate models by RF (2) to improve RF’s model performance using hyperparameter tuning method (3) to extract design parameter importance and rules from RF’s generated surrogate models. We present related work in Sect. 2, our approach in Sect. 3, experiments in Sect. 4, results and analysis in Sect. 5, and conclusions in Sect. 6.
2 Related Work
In this section, we present related work on several methods that have been used to construct surrogate models. We found that Kriging and Polynomial methods are commonly used to construct surrogate models [4, 20, 22]. Mack et al. have used Polynomial response surface approximation for multi-objective optimization of a compact liquid-rocket radial turbine in aerospace application [14]. Thorough investigations of Polynomial Regression, Multivariate Adaptive Regression Splines, Radial Basis Functions, Kriging and Bayesian Neural Networks were conducted, and some observations were presented in the following studies [10, 25]. For instance, a drawback of Polynomial models is that they have limited flexibility and need prior knowledge of underlying functions [19].
In another study, the authors used Random Forests (RF) to construct surrogate models for design optimization of a car and concluded that RF is performing as well as Kriging method [17]. Though Kriging is another well studied method for surrogate model generation, the use of Kriging method is not trivial to construct surrogate models due to its global optimization process [23] for non-experts who are unaware of Kriging methodology. On the other hand, the construction of RF is not as difficult as Kriging but still shows an equal performance. RF was also compared with Support Vector Machines, M5P and Linear Regression and the authors observed that RF is performing as well as these methods [6]. Though RF models have been shown a better performance for these two studies and also other applications, they have been rarely used for surrogate modeling in design engineering. These observations motivate us to study RF applicability for our design study problem.
Furthermore, we focused on related work on how to improve the performance of RF, and we found that hyperparameter tuning of RF could help achieve that [2, 8, 13]. Regarding this, Oshiro et al. analysed the performance of Random Forests by tuning the number of trees (Ntree) for classification tasks [16]. The authors provided insights about Ntree (threshold configurations). Diaz et al. also mentioned about hyperparameters of RF that increasing Mtry can lead to a small decrease in error rate and vice versa [8]. Similar to these studies, we focus on tuning hyperparameters of RF for regression instead of classification tasks.
Terminology: A design concept (also called an instance) is a set of design parameters (also called variables or inputs) and design objectives (also called outputs) that explain the design of Turbine Rear Structure (TRS) component. In every design concept, the design variables and objectives are the same, but the values vary. Design space exploration is investigating alternative design concepts in order to find an optimal design concept that fulfill design requirements and constraints prior to implementation. The term hyperparameter refers to the characteristic of a method. For instance, Ntree and Mtry are the hyperparameters of the RF method.
3 An Approach to Explore Design Space Using Random Forests Surrogate Models
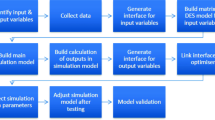
In this section, we present our approach, that is shown in Fig. 2, to explore the design space of Turbine Rear Structure through RF generated surrogate models.
3.1 Use-Case: A Design Study of Turbine Rear Structure
The geometry model of Turbine Rear Structure (TRS) is shown in Fig. 1, and it is a component of aircraft engine. TRS is a complex component of engine which involves multidisciplinary studies that address the behaviour of the design from mechanical, aerothermal and producibility aspects. For better understanding of design space of TRS, engineers divide design space into several design studies incrementally to evaluate different aspects of the proposed design, piece by piece unveiling behaviour and constraints. In this study, we use data from one of TRS design studies that focus on investigating four design parameters of hub configuration (inputs) such as hub rear stiffener height, forward hub wall angle, hub knee point radial position and bearing flange axil position shown in Fig. 1, to get better understanding about them. These design parameters are studied together with 17 other parameters related to thickness groups (engine mount, hub surface, mount sectors etc), turbine vanes and outer case. In total, 21 design parameters are used to create computer aided design (CAD) models which are analysed using finite element analysis. The outputs (design objectives) from this analysis are shown in Table 1.
For this design study, a total of 56 design concepts were generated from finite element analysis. These 56 design concepts are too small to understand the design space of parameters. At the same time, it is time-consuming to perform finite element analysis on more design concepts. Therefore, surrogate models are constructed to analyse more design concepts in order to reduce the number of simulations that are needed for design space exploration.
3.2 Surrogate Model Generation
In surrogate modelling, the aim is to determine a continuous function \(\hat{f}\) (model) of a set of design variables \(\mathbf x = x_1, x_2, ..., x_n\) from a limited amount of available data D (shown in Fig. 2(a)). The available data D represent the exact evaluations of the function f, and in general cannot carry sufficient information to uniquely identify f. Thus, surrogate modelling deals with two problems which are constructing a model \(\hat{f}\) from the available data D, and evaluating the error \(\varepsilon \) of the model [14]. The prediction of the simulation based model output using surrogate modelling approach is formulated as follows:
Where \(\hat{f}(\varvec{\mathbf {x}})\) is the predicted output and \(\varepsilon (\varvec{\mathbf {x}})\) is the error in the prediction. The construction of response surface model involves several steps (shown in Fig. 2) [18]: (1) Design of experiments: A set of design variables (\(\mathbf x = (x_1, x_2, ..., x_d)^T\), T means transpose of vector) and their values are selected (2) Numerical simulations: Let f be the black-box function (simulations), evaluate f on design points \(y_i = f(\mathbf x _i) \) where \(\mathbf{x _i}\in \mathbb {R}^d\) and \(y_i \in \mathbb {R}\) (3) Construction of response surface model: Consider the data \(D= \{(\mathbf x _1, y_1),\ldots ,(\mathbf x _n,y_n)\}\), given the data, a continuous function \(\hat{f}\) is determined to evaluate new design point \(\hat{y} = f(\hat{x_i})\) (4) Model validation: Assessing the predictive performance of \(\hat{f}\) from the available data D. We used Random Forest to construct surrogate models and the brief description of it is as follows:
Random Forests (RF) is an ensemble method that is a combination of multiple methods, and can handle nominal, categorical and continues data, thus, it is used for both classification and regression [3]. RF contains several decision trees. Each tree in the forest represents a model. It is built using a deterministic algorithm by selecting a random set of variables and random samples from the training set. Two hyperparameters of RF are needed to build a forest: Ntree - the number of trees to grow in the forest based on a bootstrap sample of observations, and Mtry - a number of features which are randomly selected for all split in the tree. The training procedure of RF is as follows (a brief visual representation is shown in Fig. 2(b)):
-
1.
From a dataset D, draw a bootstrap sample \(D'\) randomly with replacement for each tree construction.
-
2.
Build a tree T using the bootstrap sample, at each node, choose the best split among a randomly selected subset of Mtry descriptors. The tree is constructed until no further splits are possible or reaching given Node size limit.
-
3.
Repeat the \(2^{\text {nd}}\) step until user defined number of trees is reached.
When choosing the bootstrap samples to build a tree, some of the training data may be repeated and some of the samples are left out. These left out data samples are called out-of-bag samples. For RF model generation, two thirds of all training samples are used for deriving the regression function whereas one third forms the out-of-bag samples. A regression tree is built using randomly selected training samples, and out-of-bag samples are used to test for the accuracy of the tree.
3.3 Improve Random Forests Model Performance
We found that one of the ways to improve the performance of a model is hyperparameter tuning [2, 8, 13]. We use the same method to improve the performance of RF models, and the procedure is as follows. Firstly, two hyperparameters and a set of parameter configuration values are selected for parameter tuning of RF. The detailed descriptions of parameters and configurations are explained in Sect. 4.2 (Hyperparameters and Configuration Selection). Secondly, experiments are conducted to construct surrogate models using our design study data with those parameter configurations of RF. Finally, Root Mean Square Error (RMSE) is calculated for the prediction error rate of the surrogate model. The RMSE is calculated as the sum of squared differences of the predicted values and the actual values of the regression variable divided by the number of predictions as shown in Eq. 2 [24]. Where \(\hat{y}\) is the predicted value and y is the actual value.
3.4 Parameters Importance and Rules from RF Surrogate Models
As mentioned earlier in Sect. 3.2, numerical simulations use a black-box function to evaluate design points. Hence, the mapping procedure from input to output parameters are hard to interpret. Hence, if we can provide some information regarding this mapping procedure, it could help to understand the design space better and make informed decisions about design parameters. This is one of the reasons to select the RF method to construct surrogate models, because it provides parameter importance. Furthermore, it can provide rules that could help to understand the design space. For instance, we can observe where the first split is on design space and which design parameter is used for that split. In order to extract information from RF, we use the InTrees framework which is presented in [7]. The InTrees framework extracts information from the trees in the form of if-then rules, and prunes redundant rules and leaves the non-redundant rules in the forest. These rules may provide some information regarding the prediction behaviour to understand the relationship between input and output parameters. An example of the if-then rule is shown in Fig. 2(c).
3.5 Decision Support
The end goal of our design study application is to analyse design parameters (inputs) by exploring design concepts, and then to get some insights about them. For this, we use Random Forest surrogate models as a support in decision making by (1) predicting the value of design objectives for as many design concepts as possible to reduce computational expensive simulations needed to explore the design space (2) getting insights about the importance of design parameters towards the design objectives, and when needed, reduce number of parameters to narrow down its space for further analysis, and (3) extracting if-then rules that could help to better understand the reasoning of prediction behavior of the RF surrogate model.
4 Experimental Design
This section presents the experimental design to construct surrogate model by Random Forests.
4.1 Dataset Descriptions
We have a dataset D1 from our design study which contains 56 design concepts (instances). Each design concept describes a possible design of TRS which is a component of an aircraft engine. The design concepts are selected from the design space of a turbine vane using Latin hypercube sampling technique. Later, simulations were conducted using selected design concepts to get their design objectives (outputs). The 56 concepts contain 21 design variables (Sect. 3.1) and 14 design objectives with continuous values. We use these simulated design concepts to construct surrogate models. Since we have 14 outputs, we divided the dataset into 14 sub-datasets as single output design concept datasets. This means that we have an independent RF model for each output, hence 14 models. We have another dataset D2 related to TRS with 410 design concepts with three more outputs (D2-15, D2-16 and D2-17). Table 1 (second row) shows the description of design objective or outcome of TRS for all datasets. We used in total, 17 datasets for experiments, and we named them as D1-1, D1-2\(\ldots \), D2-17.
4.2 Hyperparameters and Configuration Selection
We selected Mtry and Ntree hyperparameters to tune RF. The motivation is, these parameters have an effect on model performance. For instance, a previous study states that increasing the size of tree (Ntree) can decrease the forest error rate, and decreasing number of random features (Mtry) can reduce the strength of a tree (increases the error rate) [16]. Threshold range was provided for Ntree which is 1 to 128 to increase accuracy for classification tasks [16]. We also selected a narrower range of Ntree configuration values between 10 and 130 with step size 10. We select Mtry configuration values from minimum to maximum number of input features from datasets with step size 2. For instance, for n = 5 input features, the Mtry configurations are 1, 3 and 5. We automatized hyperparameter tuning using the following procedure to get a model with a better RMSE.
-
1.
Set configuration values for Mtry and Ntree. The maximum Mtry value should be n − 1 where n is the number of features in the datasets.
-
2.
Generate possible configurations using Mtry and Ntree.
-
3.
Construct a model with single output dataset using RF.
-
4.
Repeat step 3 for each possible hyperparameter configuration value.
-
5.
Evaluate the performance of model for each hyperparameter configuration value.
-
6.
Select the model, which has least RMSE.
-
7.
Repeat steps 1–6 for every single output dataset.
4.3 Experiment
We used the selected hyperparameter configuration values (Ntree 10 to 130 with step size 10 and Mtry from 1 to 21 with step size 2) to generate possible combinations of configurations for all selected datasets. We have 143 possible parameter configurations for datasets D1-1 ..., D1-13 and 130 for D2-14 ..., D2-17. Later, we conducted the experiment to construct surrogate models using RF by tuning the selected hyperparameter’s configurations (Ntree and Mtry) with 10 fold cross-validation [12]. We measured RMSE to evaluate the prediction accuracy. We used R software environment and RF packagesFootnote 1 to conduct experiments.
5 Results and Analysis
In this section, we present the prediction error (RMSE) of RF surrogate models in order to predict the value of design objective (output) for as many design concepts (inputs) as possible, and to reduce the number of expensive simulations that are needed for design space exploration. Table 1 shows RMSE for RF with default parameter configurations (Ntree = 100 and Mtry = 5), and tuned RF. The results show that tuned RF yields the best results compared to RF with default configurations for all datasets. Furthermore, we compared our study results to those reported in [6] for the same datasets, and we found that tuned RF performs better than Support Vector Machines, Linear Regression and M5P.
In this paper, we included RMSE results (Table 1) for one Mtry configuration which gave the best results compared to the other configurations. Due to the page limit, the RMSE results for the rest of Mtry configurations are available on the online web linkFootnote 2. These RMSE results show that the prediction error is decreased by hyperparameter tuning, and we observed that Mtry has influence on the prediction error. We can support our observation on Mtry with Diaz et al.’s study observations on Mtry that shows similar effects [8], however, for classification tasks. Regarding Ntree, we observed that it has little influence on the performance. Hence, the threshold values of Ntree which are provided for classification tasks [16] and also for our configurations (Ntree: between 10 and 130) can be recommended for regression tasks too.
In order to test if Mtry has significant influence on the prediction error, we conducted the Friedman statistical test [21] to test the null hypothesis which is there is no significant difference between Mtry parameter values and predictive performance. From the Friedman statistical test, we got p-value which is less than 0.05 significant level, hence, rejecting the null hypothesis. Thus, there is a significant performance difference between different Mtry values. In addition, we conducted the post hoc Nemenyi test for pair wise comparison to see individual differences. These pair wise statistical results indicate that there is significant difference between larger Mtry configurations and smaller Mtry configurations. The post hoc Nemenyi test results are also available on the same online link (See footnote 2).
As a summary of the analysis, we see that automated hyperparameter tuning helped us to get a model with better performance. Also, it only took between 2 to 3 min to run all hyperparameter configurations. The system we used is a 64-bit Windows 7 Operating System with 2.7 GHz Intel Core i7-4600U CPU and 8 GB RAM. Since we have small sample size– and also in general, surrogate models usually are built using small size of samsples– of datasets, we believe this automated procedure has a reasonable time complexity. Thus, this procedure is recommended for design engineers when they construct surrogate models with small sample sizes using RF for hyperparameters tuning to get a model with better prediction accuracy.
5.1 Parameters Importance and Rules Extraction
In this section, we present how to get variable importance and rules from RF surrogate models. For this, we focus on one of the design objectives of the turbine rear structure (TRS) which is TRS mass (D1-11 dataset in Table 1). The measure that we used to extract parameter’s importance is the increase in mean squared error (MSE) as a result of a parameter permutation (more details on parameters importance can be found in [3]). Hence, the higher value indicates that the parameter has a high importance on the model performance (building model without this parameter causes an increase in the prediction error).
We have used a total of 21 design parameters (inputs) and the mass of TRS (design outcome or output) to build the surrogate model by RF, and the importance extracted from the surrogate model is plotted in Fig. 3. The x-axis represents the number of design parameters and the y-axis represents the importance of each of these variables. Due to the confidentiality of design parameters, we did not include their names in the plot. Figure 3 provides an idea on different design parameters’ contribution on model performance, and this analysis could help to further explore the space of design parameters. For example, we observed that parameters that are related to forward hub wall angle and hub cone mount have high importance, and inner ring reg and mount have low importance compared to other parameters. Further analysis of this example would be tune parameter configurations of high or low importance and then predict the outcomes for a better understanding of these parameters.
Furthermore, we extracted if-then rules from surrogate models for TRS mass. For a better understanding, we discretize the outcome of TRS mass into three levels with intervals (low, medium and high). There are 7 rules for low mass, 9 rules for medium and 8 rules for high mass of TRS. By looking at these rules, we can see the reasoning for the predictions that cause the low or high mass of TRS. For example, if we want to focus on minimising the mass of TRS, we use the 7 rules (1) to understand design parameters and their configurations’ contribution in predictions, (2) to narrow down the design regions (3) and then to generate more design concepts within that region to analyse the design outcome. We believe that this analysis (extracting if-then rules from surrogate models) helps to understand the design space better. Consequently, it helps to find the design concepts that minimise or maximise the mass of TRS.
6 Conclusions and Future Work
In this paper, we investigated the performance of Random Forests (RF) for surrogate modeling to support the design space exploration of Turbine Rear Structure. In order to get accurate surrogate models, we conducted hyperparameter tuning for RF. The use-case results show that the prediction performance of the model is improved by hyperparameter tuning. Additionally, we observed in our use-case results, Mtry hyperparameter has an influence on increasing the performance. Hence, our automatized hyperparameter tuning method and threshold values are recommended when using RF to get accurate surrogate models. Furthermore, we extracted design parameters’ importance and if-then rules from RF generated surrogate models to better understand the design parameters and design space of Turbine Rear Structure. In future work, we will focus on investigating RF’s applicability for other tasks such as sensitivity analysis and design optimization.
References
Amouzgar, K., Bandaru, S., Ng, A.H.: Radial basis functions with a priori bias as surrogate models: a comparative study. Eng. Appl. Artif. Intell. 71, 28–44 (2018)
Biau, G., Scornet, E.: A random forest guided tour. Test 25(2), 197–227 (2016)
Breiman, L.: Random forests. Mach. Learn. 45(1), 5–32 (2001)
Carley, K.M., Kamneva, N.Y., Reminga, J.: Response surface methodology. Technical report, DTIC Document (2004)
Chen, L., Wang, H., Ye, F., Hu, W.: Comparative study of HDMRs and other popular metamodeling techniques for high dimensional problems. Struct. Multidisc. Optim. 59(1), 21–42 (2019)
Dasari, S.K., Lavesson, N., Andersson, P., Persson, M.: Tree-based response surface analysis. In: Pardalos, P., Pavone, M., Farinella, G.M., Cutello, V. (eds.) MOD 2015. LNCS, vol. 9432, pp. 118–129. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-27926-8_11
Deng, H.: Interpreting tree ensembles with inTrees. arXiv preprint arXiv:1408.5456 (2014)
Díaz-Uriarte, R., De Andres, S.A.: Gene selection and classification of microarray data using random forest. BMC Bioinform. 7(1), 1 (2006)
Gorissen, D., Couckuyt, I., Demeester, P., Dhaene, T., Crombecq, K.: A surrogate modeling and adaptive sampling toolbox for computer based design. J. Mach. Learn. Res. 11, 2051–2055 (2010)
Jin, R., Chen, W., Simpson, T.W.: Comparative studies of metamodelling techniques under multiple modelling criteria. Struct. Multidisc. Optim. 23(1), 1–13 (2001)
Kang, E., Jackson, E., Schulte, W.: An approach for effective design space exploration. In: Calinescu, R., Jackson, E. (eds.) Monterey Workshop 2010. LNCS, vol. 6662, pp. 33–54. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-21292-5_3
Kohavi, R., et al.: A study of cross-validation and bootstrap for accuracy estimation and model selection. IJCAI 14, 1137–1145 (1995)
Liaw, A., Wiener, M.: Classification and regression by randomforest. R News 2(3), 18–22 (2002)
Mack, Y., Goel, T., Shyy, W., Haftka, R.: Surrogate model-based optimization framework: a case study in aerospace design. In: Yang, S., Ong, Y.S., Jin, Y. (eds.) Evolutionary Computation in Dynamic and Uncertain Environments. SCI, vol. 51, pp. 323–342. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-49774-5_14
Menze, B.H., Kelm, B.M., Splitthoff, D.N., Koethe, U., Hamprecht, F.A.: On oblique random forests. In: Gunopulos, D., Hofmann, T., Malerba, D., Vazirgiannis, M. (eds.) ECML PKDD 2011. LNCS (LNAI), vol. 6912, pp. 453–469. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-23783-6_29
Oshiro, T.M., Perez, P.S., Baranauskas, J.A.: How many trees in a random forest? In: Perner, P. (ed.) MLDM 2012. LNCS (LNAI), vol. 7376, pp. 154–168. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-31537-4_13
Preuss, M., Wagner, T., Ginsbourger, D.: High-dimensional model-based optimization based on noisy evaluations of computer games. In: Hamadi, Y., Schoenauer, M. (eds.) LION 2012. LNCS, pp. 145–159. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34413-8_11
Queipo, N.V., Haftka, R.T., Shyy, W., Goel, T., Vaidyanathan, R., Tucker, P.K.: Surrogate-based analysis and optimization. Prog. Aerosp. Sci. 41(1), 1–28 (2005)
Sathyanarayanamurthy, H., Chinnam, R.B.: Metamodels for variable importance decomposition with applications to probabilistic engineering design. Comput. Ind. Eng. 57(3), 996–1007 (2009)
Shan, S., Wang, G.G.: Survey of modeling and optimization strategies to solve high-dimensional design problems with computationally-expensive black-box functions. Struct. Multidisc. Optim. 41(2), 219–241 (2010)
Sheskin, D.J.: Handbook of Parametric and Nonparametric Statistical Procedures. CRC Press, Boca Raton (2003)
Simpson, T.W., Mauery, T.M., Korte, J.J., Mistree, F.: Comparison of response surface and kriging models in the multidisciplinary design of an aerospike nozzle. Institute for Computer Applications in Science and Engineering, NASA Langley Research Center (1998)
Wang, G.G., Shan, S.: Review of metamodeling techniques in support of engineering design optimization. J. Mech. Des. 129(4), 370–380 (2007)
Witten, I.H., Frank, E.: Data Mining: Practical Machine Learning Tools and Techniques. Morgan Kaufmann, San Francisco (2011)
Zhao, D., Xue, D.: A comparative study of metamodeling methods considering sample quality merits. Struct. Multidisc. Optim. 42(6), 923–938 (2010)
Acknowledgments
This work is part of the research project “Model Driven Development and Decision Support” funded by the Knowledge Foundation (grant: 20120278) in Sweden.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 IFIP International Federation for Information Processing
About this paper
Cite this paper
Dasari, S.K., Cheddad, A., Andersson, P. (2019). Random Forest Surrogate Models to Support Design Space Exploration in Aerospace Use-Case. In: MacIntyre, J., Maglogiannis, I., Iliadis, L., Pimenidis, E. (eds) Artificial Intelligence Applications and Innovations. AIAI 2019. IFIP Advances in Information and Communication Technology, vol 559. Springer, Cham. https://doi.org/10.1007/978-3-030-19823-7_45
Download citation
DOI: https://doi.org/10.1007/978-3-030-19823-7_45
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-19822-0
Online ISBN: 978-3-030-19823-7
eBook Packages: Computer ScienceComputer Science (R0)