Abstract
Assumption-based argumentation is one of the most prominent formalisms for logical (or structured) argumentation. It has been shown useful for representing defeasible reasoning and has tight links to logic programming. In this paper we study the Dung semantics for extended forms of assumption-based argumentation frameworks (ABFs), based on any contrapositive propositional logic, and whose defeasible rules are expressed by arbitrary formulas in that logic. In particular, new results on the well-founded semantics for such ABFs are reported, the redundancy of the closure condition is shown, and the use of disjunctive attacks is investigated. Finally, some useful properties of the generalized frameworks are considered.
This work is supported by the Israel Science Foundation (grant number 817/15). The first author is also supported by the Sofja Kovalevskaja award of the Alexander von Humboldt-Foundation, funded by the German Ministry for Education and Research.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
While both this paper and [13] refer to Dung semantics for simple contrapositive ABFs, the topics that each paper addresses are different, thus the papers are complementary.
- 2.
An extended abstract of this paper appears in the proceedings of AAMAS’2019.
- 3.
That is, \(\psi ,\lnot \psi \vdash \mathsf{F}\). In explosive logics every formula follows from inconsistent assertions.
- 4.
In the sequel, some proofs will be sketched or omitted altogether due to space restrictions.
- 5.
In particular, the emptyset does not defend q from the attack \(p,\lnot p \vdash \lnot q\).
- 6.
This is exactly the reason why the restriction to closed sets is imposed when standard attacks are used, while for disjunctive attacks this is not necessary.
- 7.
Note that this writing is somewhat ambiguous, since, e.g. when \(\varGamma ,Ab,\psi \) are the premises, \(\psi \) may be either a strict or a defeasible assumption. This will not cause problems in what follows.
- 8.
We refer to [13] for an example that shows that
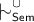 is not preferential even for ABFs with standard (non-disjunctive) attacks.
is not preferential even for ABFs with standard (non-disjunctive) attacks. - 9.
Note that by Theorem 2,
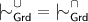 , and so
, and so 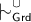 is not only cumulative, but also preferential.
is not only cumulative, but also preferential. - 10.
We note that works such as [12] use similar terminology when referring to attacks among arguments, but the nature of the attacks (disjunctive formulas vs. conjunctive formulas), as well as the context of those works (other structured frameworks), are different.
- 11.
The fact that a redundant closure condition reduces the computational complexity has been exploited in [10], for the analysis of flat ABFs (i.e., for ABFs in which no assumptions are derivable from other assumptions), in which case the closure assumption is indeed redundant. Our results now establish that for a wide class of non-flat ABFs, the closure condition can be safely dropped.
References
Amgoud, L., Besnard, P.: A formal characterization of the outcomes of rule-based argumentation systems. In: Liu, W., Subrahmanian, V.S., Wijsen, J. (eds.) SUM 2013. LNCS (LNAI), vol. 8078, pp. 78–91. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40381-1_7
Amgoud, L., Besnard, P.: Logical limits of abstract argumentation frameworks. J. Appl. Non-class. Log. 23(3), 229–267 (2013)
Arieli, O., Borg, A., Straßer, C.: Reasoning with maximal consistency by argumentative approaches. J. Log. Comput. 28(7), 1523–1563 (2018)
Bondarenko, A., Dung, P.M., Kowalski, R., Toni, F.: An abstract, argumentation-theoretic approach to default reasoning. Artif. Intell. 93(1), 63–101 (1997)
Caminada, M., Carnielli, W., Dunne, P.: Semi-stable semantics. J. Log. Comput. 22(5), 1207–1254 (2011)
Caminada, M., Schulz, C.: On the equivalence between assumption-based argumentation and logic programming. J. Artif. Intell. Res. 60, 779–825 (2017)
Cayrol, C.: On the relation between argumentation and non-monotonic coherence-based entailment. In: Proceedings of the IJCAI 1995, pp. 1443–1448 (1995)
Čyras, K., Fan, X., Schulz, C., Toni, F.: Assumption-based argumentation: disputes, explanations, preferences. In: Handbook of Formal Argumentation, pp. 2407–2456 (2018)
Čyras, K., Toni, F.: Non-monotonic inference properties for assumption-based argumentation. In: Black, E., Modgil, S., Oren, N. (eds.) TAFA 2015. LNCS (LNAI), vol. 9524, pp. 92–111. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-28460-6_6
Dimopoulos, Y., Nebel, B., Toni, F.: On the computational complexity of assumption-based argumentation for default reasoning. Artif. Intell. 141(1/2), 57–78 (2002)
Dung, P.M.: On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and n-person games. Artif. Intell. 77, 321–358 (1995)
Gabbay, D.M., Gabbay, M.: Theory of disjunctive attacks, part I. Log. J. IGPL 24(2), 186–218 (2016)
Heyninck, J., Arieli, O.: On the semantics of simple contrapositive assumption-based argumentation frameworks. In: Proceedings of the COMMA 2018. Frontiers in Artificial Intelligence and Applications, vol. 305, pp. 9–20. IOS Press (2018)
Kraus, S., Lehmann, D., Magidor, M.: Nonmonotonic reasoning, preferential models and cumulative logics. Artif. Intell. 44(1), 167–207 (1990)
Lehmann, D.J., Magidor, M.: What does a conditional knowledge base entail? Artif. Intell. 55(1), 1–60 (1992)
Rescher, N., Manor, R.: On inference from inconsistent premisses. Theory Decis. 1(2), 179–217 (1970)
Straßer, C.: Tutorial on nonmonotonic logics. In: Nat@Logic Workshop (2015)
Toni, F.: Assumption-based argumentation for epistemic and practical reasoning. Comput. Model. Law Lang. Dialogues Games Ontol. 4884, 185–202 (2008)
Vesic, S.: Identifying the class of maxi-consistent operators in argumentation. J. Artif. Intell. Res. 47, 71–93 (2013)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Heyninck, J., Arieli, O. (2019). Simple Contrapositive Assumption-Based Frameworks. In: Balduccini, M., Lierler, Y., Woltran, S. (eds) Logic Programming and Nonmonotonic Reasoning. LPNMR 2019. Lecture Notes in Computer Science(), vol 11481. Springer, Cham. https://doi.org/10.1007/978-3-030-20528-7_7
Download citation
DOI: https://doi.org/10.1007/978-3-030-20528-7_7
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-20527-0
Online ISBN: 978-3-030-20528-7
eBook Packages: Computer ScienceComputer Science (R0)





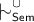 is not preferential even for ABFs with standard (non-disjunctive) attacks.
is not preferential even for ABFs with standard (non-disjunctive) attacks.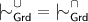 , and so
, and so 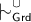 is not only cumulative, but also preferential.
is not only cumulative, but also preferential.