Skip to main content
SpringerLink
Log in

Layout-Aware Embedding for Quantum Annealing Processors

  • Conference paper
  • First Online:
High Performance Computing (ISC High Performance 2019)

Part of the book series: Lecture Notes in Computer Science ((LNTCS,volume 11501))

Included in the following conference series:

Abstract

Due to the physical limit in connectivity between qubits in Quantum Annealing Processors (QAPs), when sampling from a problem formulated as an Ising graph model, it is necessary to embed the problem onto the physical lattice of qubits. A valid mapping of the problem nodes into qubits often requires qubit chains to ensure connectivity.

We introduce the concept of layout-awareness for embedding; wherein information about the layout of the input and target graphs is used to guide the allocation of qubits to each problem node. We then evaluate the consequent impact on the sampling distribution obtained from D-Wave’s QAP, and provide a set of tools to assist developers in targeting QAP architectures using layout-awareness. We quantify the results from a layout-agnostic and a layout-aware embedding algorithm on (a) the success rate and time at finding valid embeddings, (b) the metrics of the resulting chains and interactions, and (c) the energy profile of the annealing samples. The latter results are obtained by running experiments on a D-Wave Quantum Annealer, and are directly related to the ability of the device to solve complex problems.

Our technique effectively reduces the search space, which improves the time and success rate of the embedding algorithm and/or finds mappings that result in lower energy samples from the QAP. Together, these contributions are an important step towards an understanding of how near-future Computer-Aided Design (CAD) tools can work in concert with quantum computing technologies to solve previously intractable problems.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 59.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 74.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    With ; ; ; 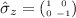\(\hat{\sigma }_\alpha ^{(i)}= \overbrace{I\otimes ... \otimes I}^{i-1} \otimes \hat{\sigma }_\alpha \overbrace{\otimes I\otimes ... \otimes I}^{N-i}\).

  2. 2.

    We also developed a flow for future QAP architectures, such as Pegasus [8], but Pegasus machines have not been made available for public usage.

References

  1. Adachi, S.H., Henderson, M.P.: Application of quantum annealing to training of deep neural networks, p. 18, October 2015. arXiv preprint: arXiv:1510.06356

  2. Amin, M.H., Andriyash, E., Rolfe, J., et al.: Quantum Boltzmann machine. Phys. Rev. X 8(2) (2018). https://doi.org/10.1103/PhysRevX.8.021050

  3. Asghar, A., Parvez, H.: An improved diffusion based placement algorithm for reducing interconnect demand in congested regions of FPGAs. Int. J. Reconfigurable Comput. 2015, 1–10 (2015). http://www.hindawi.com/journals/ijrc/2015/756014/

    Article  Google Scholar 

  4. Benedetti, M., Realpe-Gómez, J., Perdomo-Ortiz, A.: Quantum-assisted Helmholtz machines: a quantum-classical deep learning framework for industrial datasets in near-term devices. Quantum Sci. Technol. 3(3), 34007 (2018). https://doi.org/10.1088/2058-9565/aabd98

    Article  Google Scholar 

  5. Bian, Z., Chudak, F., Israel, R., et al.: Discrete optimization using quantum annealing on sparse Ising models. Front. Phys. 2, 56 (2014). http://journal.frontiersin.org/article/10.3389/fphy.2014.00056

    Article  Google Scholar 

  6. Bian, Z., Chudak, F., Israel, R., et al.: Mapping constrained optimization problems to quantum annealing with application to fault diagnosis. Front. ICT 3, 14 (2016). http://journal.frontiersin.org/article/10.3389/fict.2016.00014

    Article  Google Scholar 

  7. Bian, Z., Chudak, F., Macready, W.G., et al.: Experimental determination of Ramsey numbers. Phys. Rev. Lett. 111(13) (2013). https://doi.org/10.1103/PhysRevLett.111.130505

  8. Boothby, K., Bunyk, P., Raymond, J., Roy, A.: Next-generation topology of D-wave quantum processors. Technical report (2019). https://www.dwavesys.com/sites/default/files/14-1026A-C_Next-Generation-Topology-of-DW-Quantum-Processors.pdf

  9. Boothby, T., King, A.D., Roy, A.: Fast clique minor generation in Chimera qubit connectivity graphs. Quantum Inf. Process. 15(1), 495–508 (2016). https://doi.org/10.1007/s11128-015-1150-6

    Article  MathSciNet  MATH  Google Scholar 

  10. Bunyk, P.I., Hoskinson, E.M., Johnson, M.W., et al.: Architectural considerations in the design of a superconducting quantum annealing processor. IEEE Trans. Appl. Supercond. 24(4), 1–10 (2014). https://arxiv.org/abs/1401.5504

    Article  Google Scholar 

  11. Cai, J., Macready, W.G., Roy, A.: A practical heuristic for finding graph minors. Quantum (2014). http://arxiv.org/abs/1406.2741

  12. Choi, V.: Minor-embedding in adiabatic quantum computation: I. The parameter setting problem. Quantum Inf. Process. 7(5), 193–209 (2008). https://doi.org/10.1007/s11128-008-0082-9

    Article  MathSciNet  MATH  Google Scholar 

  13. Choi, V.: Minor-embedding in adiabatic quantum computation: II. Minor-universal graph design. Quantum Inf. Process. 10(3), 343–353 (2011). https://doi.org/10.1007/s11128-010-0200-3

    Article  MathSciNet  MATH  Google Scholar 

  14. D-Wave Systems Inc.: D-Wave Leap (2018). https://cloud.dwavesys.com/leap/

  15. D-Wave Systems Inc.: Source Repository for MinorMiner. Version 0.1.7 (2019). https://github.com/dwavesystems/minorminer

  16. Djidjev, H.N., Chapuis, G., Hahn, G., Rizk, G.: Efficient combinatorial optimization using quantum annealing, January 2018. https://arxiv.org/abs/1801.08653

  17. Dorband, J.E.: Stochastic characteristics of Qubits and Qubit chains on the D-Wave 2X, June 2016. http://arxiv.org/abs/1606.05550

  18. Douglass, A., King, A.D., Raymond, J.: Constructing SAT filters with a quantum annealer. In: Heule, M., Weaver, S. (eds.) SAT 2015. LNCS, vol. 9340, pp. 104–120. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-24318-4_9

    Chapter  MATH  Google Scholar 

  19. Harris, R., Johnson, M.W., Lanting, T., et al.: Experimental investigation of an eight-qubit unit cell in a superconducting optimization processor. Phys. Rev. B Condens. Matter Mater. Phys. 82(2), 24511 (2010). https://doi.org/10.1103/PhysRevB.82.024511

    Article  Google Scholar 

  20. Harris, R., Sato, Y., Berkley, A.J., et al.: Phase transitions in a programmable quantum spin glass simulator. Science (New York) 361(6398), 162–165 (2018). http://www.ncbi.nlm.nih.gov/pubmed/30002250

    Article  MathSciNet  Google Scholar 

  21. Huff, T., Labidi, H., Rashidi, M., et al.: Binary atomic silicon logic. Nat. Electron. 1(12), 636–643 (2018). http://arxiv.org/abs/1706.07427, http://www.nature.com/articles/s41928-018-0180-3

    Article  Google Scholar 

  22. Jiang, S., Britt, K.A., McCaskey, A.J., et al.: Quantum annealing for prime factorization, April 2018. http://arxiv.org/abs/1804.02733

  23. Johnson, M.J.: Future hardware directions of quantum annealing (2018). https://www.dwavesys.com/sites/default/files/mwj_dwave_qubits2018.pdf

  24. Könz, M.S., Mazzola, G., Ochoa, A.J., et al.: Uncertain fate of fair sampling in quantum annealing, June 2018. http://arxiv.org/abs/1806.06081

  25. Korenkevych, D., Xue, Y., Bian, Z., et al.: Benchmarking quantum hardware for training of fully visible Boltzmann machines, November 2016. http://arxiv.org/abs/1611.04528

  26. Li, R.Y., Di Felice, R., Rohs, R., Lidar, D.A.: Quantum annealing versus classical machine learning applied to a simplified computational biology problem. NPJ Quantum Inf. 4(1), 14 (2018). http://www.nature.com/articles/s41534-018-0060-8

    Article  Google Scholar 

  27. Lucas, A.: Ising formulations of many NP problems. Front. Phys. 2, 5 (2014). https://www.frontiersin.org/article/10.3389/fphy.2014.00005

    Article  Google Scholar 

  28. Mandrà, S., Zhu, Z., Katzgraber, H.G.: Exponentially biased ground-state sampling of quantum annealing machines with transverse-field driving Hamiltonians. Phys. Rev. Lett. 118(7), 070502 (2017). https://doi.org/10.1103/PhysRevLett.118.070502

    Article  Google Scholar 

  29. McMurchie, L., Ebeling, C.: PathFinder: a negotiation-based performance-driven router for FPGAs. In: Proceedings of the 1995 ACM Third International Symposium on Field-programmable Gate Arrays, FPGA 1995, pp. 111–117. ACM, New York (1995). http://doi.acm.org/10.1145/201310.201328

  30. Mishra, A., Albash, T., Lidar, D.A.: Finite temperature quantum annealing solving exponentially small gap problem with non-monotonic success probability. Nat. Commun. 9(1), 2917 (2018). http://www.nature.com/articles/s41467-018-05239-9

    Article  Google Scholar 

  31. Mott, A., Job, J., Vlimant, J.R., et al.: Solving a Higgs optimization problem with quantum annealing for machine learning. Nature 550(7676), 375–379 (2017). https://doi.org/10.1038/nature24047

    Article  Google Scholar 

  32. Pakin, S.: Performing fully parallel constraint logic programming on a quantum annealer, March 2018. https://doi.org/10.1017/S1471068418000066

    Article  MathSciNet  Google Scholar 

  33. Pakin, S.: Personal communication via email (2018)

    Google Scholar 

  34. Perdomo Ortiz, A., Fluegemann, J., Narasimhan, S., et al.: A quantum annealing approach for fault detection and diagnosis of graph-based systems, February 2015. https://doi.org/10.1140/epjst/e2015-02347-y

    Article  Google Scholar 

  35. Pinilla, J.P.: Source repository for embedding methods (2019). https://github.com/joseppinilla/embedding-methods

  36. Preskill, J.: Quantum computing in the NISQ era and beyond. Quantum 2, 79 (2018). https://arxiv.org/abs/1801.00862, https://doi.org/10.22331/q-2018-08-06-79, https://quantum-journal.org/papers/q-2018-08-06-79/

    Article  Google Scholar 

  37. Pudenz, K.L., Albash, T., Lidar, D.A.: Quantum annealing correction for random Ising problems. Phys. Rev. A Atomic Mol. Opt. Phys. 91(4) (2015). https://doi.org/10.1103/PhysRevA.91.042302

  38. Ren, H., Pan, D.Z., Alpert, C.J., Villarrubia, P.: Diffusion-based placement migration. In: Proceedings of the 42nd Annual Conference on Design Automation, DAC 2005, p. 515 (2005). http://doi.acm.org/10.1145/1065579.1065712

  39. Retallick, J., Babcock, M., Aroca-Ouellette, M., et al.: Embedding of quantum-dot cellular automata circuits onto a quantum annealing processor. In: 2014 Conference on Optoelectronic and Microelectronic Materials and Devices, COMMAD 2014, pp. 200–203, December 2014. https://doi.org/10.1109/COMMAD.2014.7038689

  40. Rieffel, E.G., Venturelli, D., O’Gorman, B., et al.: A case study in programming a quantum annealer for hard operational planning problems. Quantum Inf. Process. 14(1), 1–36 (2014). https://doi.org/10.1007/s11128-014-0892-x

    Article  MATH  Google Scholar 

  41. Steiger, D.S., Rønnow, T.F., Troyer, M.: Heavy tails in the distribution of time to solution for classical and quantum annealing. Phys. Rev. Lett. 115(23) (2015). http://arxiv.org/abs/1504.07991, https://doi.org/10.1103/PhysRevLett.115.230501

  42. Su, J., He, L.: Fast embedding of constrained satisfaction problem to quantum annealer with minimizing chain length. In: 2017 54th ACM/EDAC/IEEE Design Automation Conference (DAC), pp. 1–6. ACM Press, New York, June 2017. http://dl.acm.org/citation.cfm?doid=3061639.3062246

  43. Su, J., Tu, T., He, L.: A quantum annealing approach for Boolean satisfiability problem. In: Proceedings of the 53rd Annual Design Automation Conference, DAC 2016, pp. 1–6. ACM Press, New York (2016). http://dl.acm.org/citation.cfm?doid=2897937.2897973

  44. Venturelli, D., Mandrà, S., Knysh, S., et al.: Quantum optimization of fully connected spin glasses. Phys. Rev. X 5(3) (2015). https://arxiv.org/abs/1406.7553

  45. Venturelli, D., Marchand, D.J.J., Rojo, G.: Quantum annealing implementation of job-shop scheduling, June 2015. http://arxiv.org/abs/1506.08479

  46. Walus, K., Dysart, T.J., Jullien, G.A., Budiman, R.A.: QCADesigner: a rapid design and simulation tool for quantum-dot cellular automata. IEEE Trans. Nanotechnol. 3, 26–31 (2004). http://ieeexplore.ieee.org/document/1278264/

    Article  Google Scholar 

  47. Zaribafiyan, A., Marchand, D.J., Changiz Rezaei, S.S.: Systematic and deterministic graph minor embedding for Cartesian products of graphs. Quantum Inf. Process. 16(5), 136 (2017). https://doi.org/10.1007/s11128-017-1569-z

    Article  MathSciNet  MATH  Google Scholar 

  48. Zick, K.M., Shehab, O., French, M.: Experimental quantum annealing: case study involving the graph isomorphism problem. Sci. Rep. 5(1), 11168 (2015). http://www.nature.com/articles/srep11168

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. University of British Columbia, Vancouver, BC, Canada

    Jose P. Pinilla & Steven J. E. Wilton

Authors
  1. Jose P. Pinilla
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Steven J. E. Wilton
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jose P. Pinilla .

Editor information

Editors and Affiliations

  1. University of Edinburgh, Edinburgh, UK

    Michèle Weiland

  2. Helmholtz-Zentrum Dresden-Rossendorf (HZDR), Dresden, Germany

    Guido Juckeland

  3. Technical University of Munich, Munich, Germany

    Carsten Trinitis

  4. Ohio State University, Columbus, USA

    Ponnuswamy Sadayappan

Rights and permissions

Reprints and permissions

Copyright information

© 2019 Springer Nature Switzerland AG

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Pinilla, J.P., Wilton, S.J.E. (2019). Layout-Aware Embedding for Quantum Annealing Processors. In: Weiland, M., Juckeland, G., Trinitis, C., Sadayappan, P. (eds) High Performance Computing. ISC High Performance 2019. Lecture Notes in Computer Science(), vol 11501. Springer, Cham. https://doi.org/10.1007/978-3-030-20656-7_7

Download citation

  • DOI: https://doi.org/10.1007/978-3-030-20656-7_7

  • Published:

  • Publisher Name: Springer, Cham

  • Print ISBN: 978-3-030-20655-0

  • Online ISBN: 978-3-030-20656-7

  • eBook Packages: Computer ScienceComputer Science (R0)

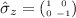Publish with us

Policies and ethics

Search

Navigation