Abstract
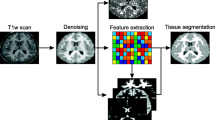
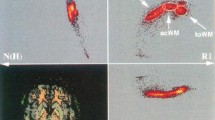
Accurate segmentation of cerebral structures remains, after two decades of research, a complex task. In particular, obtaining satisfactory results in terms of topology, in addition to quantitative and geometrically correct properties is still an ongoing issue. In this paper, we investigate how recent advances in multilabel topology and homotopy-type preserving transformations can be involved in the development of multiscale topological modelling of brain structures, and topology-based post-processing of segmentation maps of brain MR images. In this context, a preliminary study and a proof-of-concept are presented.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Bai, Y., Han, X., Prince, J.L.: Digital topology on adaptive octree grids. J. Math. Imaging Vis. 34(2), 165–184 (2009)
Bazin, P.-L., Ellingsen, L.M., Pham, D.L.: Digital homeomorphisms in deformable registration. In: Karssemeijer, N., Lelieveldt, B. (eds.) IPMI 2007. LNCS, vol. 4584, pp. 211–222. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-73273-0_18
Bazin, P.L., Pham, D.L.: Topology correction of segmented medical images using a fast marching algorithm. Comput. Methods Programs Biomed. 88(2), 182–190 (2007)
Bazin, P.L., Pham, D.L.: Topology-preserving tissue classification of magnetic resonance brain images. IEEE Trans. Med. Imaging 26(4), 487–496 (2007)
Caldairou, B., et al.: Segmentation of the cortex in fetal MRI using a topological model. In: International Symposium on Biomedical Imaging (ISBI), Proceedings, pp. 2045–2048 (2011)
Caldairou, B., Passat, N., Habas, P.A., Studholme, C., Rousseau, F.: A non-local fuzzy segmentation method: application to brain MRI. Pattern Recognit. 44(9), 1916–1927 (2011)
Cointepas, Y., Bloch, I., Garnero, L.: A cellular model for multi-objects multi-dimensional homotopic deformations. Pattern Recognit. 34(9), 1785–1798 (2001)
Couprie, M., Bertrand, G.: New characterizations of simple points in 2D, 3D, and 4D discrete spaces. IEEE Trans. Pattern Anal. Mach. Intell. 31(4), 637–648 (2009)
Damiand, G., Dupas, A., Lachaud, J.O.: Fully deformable 3D digital partition model with topological control. Pattern Recognit. Lett. 32(9), 1374–1383 (2011)
Faisan, S., Passat, N., Noblet, V., Chabrier, R., Meyer, C.: Topology preserving warping of 3-D binary images according to continuous one-to-one mappings. IEEE Trans. Image Process. 20(8), 2135–2145 (2011)
Han, X., Xu, C., Prince, J.L.: A topology preserving level set method for geometric deformable models. IEEE Trans. Pattern Anal. Mach. Intell. 25(6), 755–768 (2003)
Kong, T.Y.: A digital fundamental group. Comput. Graph. 13(2), 159–166 (1989)
Kong, T.Y., Rosenfeld, A.: Digital topology: introduction and survey. Comput. Vis. Graph. Image Process. 48(3), 357–393 (1989)
Kriegeskorte, N., Goebel, N.: An efficient algorithm for topologically correct segmentation of the cortical sheet in anatomical MR volumes. NeuroImage 14(2), 329–346 (2001)
Mangin, J.F., Frouin, V., Bloch, I., Régis, J., López-Krahe, J.: From 3D magnetic resonance images to structural representations of the cortex topography using topology preserving deformations. J. Math. Imaging Vis. 5(4), 297–318 (1995)
Mazo, L.: A framework for label images. In: Ferri, M., Frosini, P., Landi, C., Cerri, A., Di Fabio, B. (eds.) CTIC 2012. LNCS, vol. 7309, pp. 1–10. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-30238-1_1
Mazo, L., Passat, N., Couprie, M., Ronse, C.: Digital imaging: a unified topological framework. J. Math. Imaging Vis. 44(1), 19–37 (2012)
Mazo, L., Passat, N., Couprie, M., Ronse, C.: Topology on digital label images. J. Math. Imaging Vis. 44(3), 254–281 (2012)
Pham, D.L., Bazin, P.L., Prince, J.L.: Digital topology in brain imaging. IEEE Signal Process. Mag. 27(4), 51–59 (2010)
Poupon, F., Mangin, J.-F., Hasboun, D., Poupon, C., Magnin, I., Frouin, V.: Multi-object deformable templates dedicated to the segmentation of brain deep structures. In: Wells, W.M., Colchester, A., Delp, S. (eds.) MICCAI 1998. LNCS, vol. 1496, pp. 1134–1143. Springer, Heidelberg (1998). https://doi.org/10.1007/BFb0056303
Saha, P.K., Strand, R., Borgefors, G.: Digital topology and geometry in medical imaging: a survey. IEEE Trans. Med. Imaging 34(9), 1940–1964 (2015)
Ségonne, F.: Active contours under topology control - genus preserving level sets. Int. J. Comput. Vis. 79(2), 107–117 (2008)
Siqueira, M., Latecki, L.J., Tustison, N.J., Gallier, J.H., Gee, J.C.: Topological repairing of 3D digital images. J. Math. Imaging Vis. 30(3), 249–274 (2008)
Tor-Díez, C., Passat, N., Bloch, I., Faisan, S., Bednarek, N., Rousseau, F.: An iterative multi-atlas patch-based approach for cortex segmentation from neonatal MRI. Comput. Med. Imaging Graph. 70, 73–82 (2018)
Acknowledgements
The research leading to these results has been supported by the ANR MAIA project (http://recherche.imt-atlantique.fr/maia), grant ANR-15-CE23-0009 of the French National Research Agency; INSERM and Institut Mines Télécom Atlantique (Chaire “Imagerie médicale en thérapie interventionnelle”); the Fondation pour la Recherche Médicale (grant DIC20161236453); and the American Memorial Hospital Foundation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Tor-Díez, C. et al. (2019). Multilabel, Multiscale Topological Transformation for Cerebral MRI Segmentation Post-processing. In: Burgeth, B., Kleefeld, A., Naegel, B., Passat, N., Perret, B. (eds) Mathematical Morphology and Its Applications to Signal and Image Processing. ISMM 2019. Lecture Notes in Computer Science(), vol 11564. Springer, Cham. https://doi.org/10.1007/978-3-030-20867-7_36
Download citation
DOI: https://doi.org/10.1007/978-3-030-20867-7_36
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-20866-0
Online ISBN: 978-3-030-20867-7
eBook Packages: Computer ScienceComputer Science (R0)