Enhanced Parallel Generation of Tree Structures for the Recognition of 3D Images

Abstract

Segmentations of a digital object based on a connectivity criterion at n-xel or sub-n-xel level are useful tools in image topological analysis and recognition. Working with cell complex analogous of digital objects, an example of this kind of segmentation is that obtained from the combinatorial representation so called Homological Spanning Forest (HSF, for short) which, informally, classifies the cells of the complex as belonging to regions containing the maximal number of cells sharing the same homological (algebraic homology with coefficient in a field) information. We design here a parallel method for computing a HSF (using homology with coefficients in $\mathbb {Z}/2\mathbb {Z}$) of a 3D digital object. If this object is included in a 3D image of $m_1\times m_2 \times m_3$ voxels, its theoretical time complexity order is near $O(log(m_1+m_2+m_3))$, under the assumption that a processing element is available for each voxel. A prototype implementation validating our results has been written and several synthetic, random and medical tridimensional images have been used for testing. The experiments allow us to assert that the number of iterations in which the homological information is found varies only to a small extent from the theoretical computational time.

Work supported by the Spanish research projects TOP4COG, MTM2016-81030-P (AEI/FEDER,UE), COFNET (AEI/FEDER,UE), the VPPI of University of Seville and the Austrian Science Fund FWF-P27516.

1 Introduction

Using the analogy that a digital image can be seen as a puzzle of (initially, small) pieces, topological analysis and recognition problems can be rethought in terms of reconstructing the image as a puzzle of big pieces which are maximally stable with regards some connectivity criterion. This maximal stability of the regions mean that if one of these regions increase in size, the preservation of the topological criterion is lost. This perspective is not new [2, 7, 10] and exhibits nowadays fruitful results in object recognition. Working with a cell complex analogous of a 3D digital image, we are mainly interested here in using the topological invariant of homology (concretely, algebraic homology with coefficient in a field) as main argument in the topological criterion. Succinctly, a Homological Spanning Forest (HSF, for short) of a cell complex, notion developed in [1, 8], is a set of trees, in which each of them is a path-connected representation of a maximal stable homological region, whose nodes are the cells of that region. In this paper, a parallel ambiance-based algorithm for computing a HSF is for the first time implemented and tested.

2 Enhanced Parallel Generation of MrSF and HSF

Given a 3D digital object D included in a 3D digital image $I_D$, the scenario in which we need to “embed” $I_D$ based on cubical voxel is that of an abstract cubical cell complex (or ACC, for short), denoted $Cell(I_D)$, and having as 0-cells the voxels of $I_D$ and as 3-cells the 0-dimensional corners of the voxels. In our parallel framework we define one processing element ($\mathsf {PE}$) per voxel. The 0-cells inherit the properties (such as color; black or white from now on) of the actual voxels of $I_D$, the 1-cells are defined by the set of two 6-adjacent voxels, 2-cells by sets of four mutually 6-adjacent voxels and 3-cells by sets of eight mutually 6-adjacent voxels.

Fig. 1.

A ring perpendicular to Y axis with an associated MrSF.

With the previous scenario of cells over the canvas, an initial HSF of the whole image, called Morse Spanning Forest ($MrSF(I_D)$ for short), is built. It is necessary to emphasize that our construction method may initially provide a set of graphs (not necessarily trees) that will be then pruned to be trees, so that parallel computing is promoted. An $MrSF(I_D)$ will be composed by a set of $(k,k+1)$-trees ($k=0,1,2$) of size n, having as nodes cells of dimension k and (if $n>1$) cells of dimension $k+1$, and having as edges some incidence relations between these cells (called $(k,k+1)$-edges). In $MrSF(I_D)$, there is one (0, 1)-tree, one (2, 3)-tree and possibly several (1, 2)-trees.

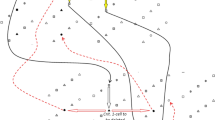
In Fig. 1, a visual example of all the necessary cells and trees of the MrSF are depicted. The circles, triangles, squares and stars represent 0-cells, 1-cells, 2-cells and 3-cells, respectively. There are (0, 1), (1, 2) and (2, 3) trees, represented by red, yellow and blue lines respectively.

The main steps of the complete construction process are shown in Fig. 2 and will be detailed in the sequel. From now on, and for clarity purposes, we restrict ourselves to work with 6-adjacency for any (background or foreground) voxel.

A complete implementation of the algorithm has been done in MATLAB / OCTAVE language [9]. This language has been chosen to favor an inherent parallel codifying and special care has been taken to promote element-by-element matrix operations whenever possible. These operations can be executed theoretically in a fully parallel manner. Only a few parts of the whole process cannot be executed with this kind of operations, thus diverging the theoretical timing order from O(1), and yielding to a few loop structures including loop-carried dependencies (thus preventing ideal parallelism [4]).

Fig. 2.

Main steps of the parallel homological segmentation of a digital object.

The proposed algorithm is divided into the three following steps, which result to be close to the logarithm of the sum of each dimension, that is, $log_2 (m_1 + m_2 + m_3)$. From now on, Foreground will be denoted as FG and Background as BG.

(a) MrSF construction at local level: Activation of processing units.

We construct $(k,k+1)$-edges of the $MrSF(I_D)$ using primal and dual $(k,k+1)$-vectors. Given two incidence cells c and $c'$ of dimensions k and $k+1$ respectively, a primal (resp. dual) $(k,k+1)$ vector $(c,c')$ (resp. $(c',c)$) connects the tail c (resp. $c'$) with the head $c'$ (resp. c). A k-crack is the set of $(k,k+1)-edges$ representing the boundary relations of a $k+1$-cell, in which only one primal vector exists (being the rest dual ones) (see Fig. 3). We say that one crack belongs to the FG (resp. to the BG) if the tail of its primal vector is a cell of the FG (resp. of the BG).

We will limit ourselves to say that for three dimensional images, there are nine possible activation states for any $\mathsf {PE}$. One of these states is pictured in Fig. 3.

Fig. 3.

An activation state of the processing unit showing its eight active cells, primal and dual activation vectors and associated cracks. The 0-cell (x, y, z) is drawn with a circle, the 1-cells with triangles, the 2-cells with squares and the 3-cell with a star. The active primal vectors are drawn with an arrow and using different colors depending on its dimension. (Color figure online)

Figure 1 shows an example of the final trees. FG cells are drawn with solid shapes (circle, triangles, squares and stars, depending on their dimension), and hollow shapes are used for BG cells. In this case, primal (0, 1) vectors are represented with red lines inside each $\mathsf {PE}$, and there is only one primal (0, 1) vector for each voxel. Note that there is only one dual vector (going form triangles to circles towards positive directions) for each 1-cell belonging to the (0,1) tree. Rules for the rest of dual vectors are similar; however in the case of the (1,2) and (2,3) trees, up to two dual vectors can go from a $(j+1)$-cell to a j-cell.

An obvious tree preservation rule must be kept at this stage: only those dual vectors that connect the same dimensional tree are allowed. Bearing in mind 6-adjacency and in order to promote parallelism, cracks are only defined towards positive directions: +X, +Y, +Z. These cracks will allow to build the different trees for a given image. Note that dual inter-voxel connections can be extensive, that is, we can activate all the possible dual vectors that do not contravene the tree allocation for each cell. However, as we are interested in building trees (not graphs) for an efficient parallel processing of crack transports, some dual (2,1) vectors must not be activated in our current implementation. More exactly, for those j-cells that can receive two dual vectors coming from $(j+1)$-cells, only one of them is activated.

For activating in parallel all the processing units of $ACC(I_D)$, we use local MrSF rules. As each $\mathsf {PE}$ can compute its state with no dependencies to the rest of $\mathsf {PE}$, this step is fully parallel, that is, O(1). In this step we proceed so that the number of critical cracks in the MrSF is maintained to the minimum possible (considering only local interactions between neighboring voxels). Critical cracks, are those having on its border both, background and foreground cells.

Critical cracks are drawn using thicker lines (using the color convention in Fig. 1). In the case of a ring (Fig. 1), FG contains one critical 0-crack and one critical 1-crack, and BG contains one critical 0-crack, one critical 1-crack and one critical 2-crack.

The main advantage of this local MrSF construction method, is that it can be computed in a fully parallel manner for each voxel.

(b) Global MrSF construction

Once a local MrSF has been built, the MrSF global trees are to be computed and labelled.

This labeling consists of tracking the label from every cell to a new one. Most of these algorithms do this tracking by using the number of the label stored at each site [5]. That is, they compute label[i] = label[label[i]] until the label remains unchanged. In our case, we use two additional pieces of information: (a) The exact knowledge of which cracks are critical (whose labels will remain unchanged); (b) The magnitudes and directions of the hops from one cell to the root. Note that the first hop is immediately given by the MrSF local information.

In order to build trees in this stage, additional prunings within the resulting graphs might be done for the (1,2) cracks.

According to the definition of primal and dual vectors of previous stages, it is obvious that the maximum distance between two cells is ($m_1+ m_2 + m_3$). Besides, using the process label[i] = label[label[i]], the hop magnitudes increases in a geometric manner of ratio 2. Hence the maximum time order for this stage is $log_2$ ($m_1+ m_2 + m_3$) (Fig. 5).

(c) Final HSF construction via crack transports

The final step consists of minimizing the number of critical cracks, giving rise to a new MrSF. That means, that within this MrSF, if we only consider cells belonging to D, we have an HSF of D. From now on, this final MrSF will be named as HSF(D). As an example, Fig. 4 (top) contains an MrSF and an HSF(D) (bottom) of an object D composed of three parallel segments. The first MrSF contains three critical 0-cracks and two critical 1-cracks for the FG (drawn with thicker red and yellow lines, resp.) and the HSF(D) contains only one critical 0-crack.

To clarify a transport operation, only one pair of the (0,1)-tree links that are to be transported have been rounded by a discontinuous oval in the MrSF. Those links are transported to the wider orange links (see the oval drawn at the HSF), so that they “close” correctly the (0,1)-tree. Another pair of (1,2)-tree links is also transported for this critical crack. Likewise, the same transport operations are done for the other pair of critical 0-crack and 1-crack. Obviously, the final HSF contains only one critical FG 0-crack, being the representative of the FG CC (connected component).

Fig. 4.

A figure composed of three segments parallel to the axis (a total of 5 black voxels). Top: MrSF, which contains 3 critical 0-cracks and 2 critical 1-cracks for the FG (thicker red and yellow segments). Bottom: HSF, which contains only one critical FG 0-crack. (Color figure online)

The key point for transforming an $MrSF(I_D)$ into an HSF(D) is the achievement of the best parallelism degree. This is done as follows. For each critical MrSF 0-crack, we calculate in parallel the movements along (1,2) and (0,1) trees. Firstly, there are six possible paths leaving from each critical 0-cell and moving through the (1,2)-tree. One of them is selected for every critical MrSF 0-crack, and the (1,2)-trees (tracking frontier digital surfaces, which can be defined in a similar manner to [6]), fall onto the corresponding 2-cells. From these 2-cells, it is resolved what critical 1-crack has a primal vector to them. Then, every 1-cell has two incident 0-cells, and the two back movements for these 0-cells are computed in parallel in order to determine if the couple of 0/1-cells can be eliminated, and so, the transport made. The movements of these 0-cells through the (0,1)-tree yield to three different cases (processed in an independent and parallel manner for each couple of 0/1-cells). These cases are: (a) the 1-cell can be deleted (a crack transport is done) with the initial critical 0-cell, because only one of its two (0,1) paths fell into the initial 0-cell; (b) the 1-cell is the representative of a tunnel (it is a true critical 1-cell), since these two (0,1) paths fell into the same 0-cell; (c) nothing can be determined, because the two (0,1) paths fell into two different 0-cells (in this case, the 1-cell remains the same).

Note that moving along trees guarantees that the uniqueness in the selection of the different couples of 0/1-cells is ensured, and therefore there is no need for synchronization primitives. In this sense, perfect parallelism is achieved in these six paths, thus, their time order can be considered as O(1). Summing up, for each critical MrSF 0-crack, six set of paths must be computed (all the paths of each set in parallel). Likewise, for the pairing of couples of critical MrSF 1/2-crack, a similar parallel procedure can be performed, preserving time order as O(1). The number of incident cells is inferior in this ulterior pairing.

Nevertheless, the transports along these six paths for couples of 0/1-cells and two paths for couples of 1/2-cells do not imply that complete pairing has been done and that these transports would give us the HSF. There are complex shapes that need some subsequent iterations. The exact form of these shapes will be studied elsewhere; for the present work, the experimental results of next section reveal that the number q of subsequent iterations needed for different types of images is less than 5 for most of the analyzed 3D images. Besides, some of the tested images required a sequential stage of 0/1 cell coupling that cannot be processed in parallel. This is due to the necessary pruning of some (1,2) vectors done in the previous stage (b) (Global MrSF construction). This pruning implies that some paths along the whole (1,2) tree are lost. As illustrated in the next section, the number of sequential transports (denoted as $s_{01}$ in Fig. 5) represents less than 0.5% of the number of voxels even for random images, being around ten times inferior for the analyzed natural images. The pruning was also done for the inverse path 2/1/2, which means that some 1/2 transports can either be done in parallel (which number is denoted as $s_{12}$ in Fig. 5). Nevertheless, for real or random 3D images the percentage of these sequential 1/2 transports is negligible. A further discussion of this aspect can be found in the next section.

Fig. 5.

Time orders for the different steps of HSF computation considering $m_1 \times m_2 \times m_3$ computation processors. $s_{01}$ and $s_{12}$ are the number of sequential cancellations of remaining 0/1 and 1/2 cells resp. (after the parallel cancellation of these pairs).

In summary, time order of one parallel step of this stage (c) is O(1). Besides, a small number q of parallel transport iterations is required for most of the images (see next section). Finally, time order would diverges from O(1) only for the small percentage of sequential transports. Figure 5 summarizes the time orders for the different steps of the whole HSF calculation considering $m_1 \times m_2 \times m_3$ computation processors. One final remark that highlights a practical significance to our method is that many useful geometric properties (area, perimeter, etc.) can be computed at the same time and also in parallel with the HSF.

3 Experimental Results and Conclusions

Firstly synthetic Menger sponges were used to test the results of the parallel algorithm by comparing the outputs with that of the algebraic AT-model [3]. Experiments were performed using fractal modifications of the Menger Sponge. The initial structures used to generate these new fractals were constructed filling planes (OX, OY and/or OZ) within the Menger Sponges of recursion 2 and 3 for different values of x, y and z. In all cases the first parallel transport iteration of 0/1 cell pairs yielded to the correct result. However, the results for the 1/2 pairs were very divergent. On one hand, for some sponges the final HSF was reached through our parallel transportation method; on the other hand, for some others the parallel transports produce moderate results (around a fifty percent of sequential 1/2 pair transports were required).

Table 1. Mean number of critical cracks for the first four parallel and last sequential transport iterations of 0/1 cell pairs, and for the following parallel and final sequential 1/2 cell transport, for a set of five B/W $30\times 30\times 30$ random images with a 50/50 probability for colors, surrounded by six thin faces of BG voxels (rows 1–3). Rows 4–12: Same evolution of the number of critical cracks for three trabecular bone images of sizes $43\times 43\times 9$, $64\times 64\times 13$, and $43\times 43\times 9$ (rows 4–6, 7–9 and 8–12 resp.). The last three columns indicate the mean percentage of parallel transports achieved: in the first iteration for 0/1 pairs, after the fourth iteration for 0/1 pairs, and for the 1/2 pair transport, resp.

No doubt that synthetic images are very peculiar and the parallel processing of the HSF can present strange results. On the contrary, parallel computing is very efficient for random images, and even more for real medical images, as shown below. For small random images (up to $15\times 15\times 15$) the proposed method was almost perfect: the final HSF is completed in a fully parallel manner for almost 100% of the tested images. Table 1 (rows 1–3) shows the mean number of critical cracks for the first four parallel and last sequential transport iterations of 0/1 cell pairs, and for the following parallel and final sequential transport of 1/2 cell pairs for a set of five $30\times 30\times 30$ B/W random images (which were generated using a 50/50 probability for colors, and surrounded by six thin faces of BG voxels according to our working premises). Actually, a fifth iteration would transport another one or two 0/1 pairs more for two of the bigger tested images, although for the sake of simplifying the tables, it has not been exposed. The last three columns reveal patently the efficiency of our parallel processing: a first phase of parallel 0/1 transports reached more that three quarters of the total necessary transports. After the fourth parallel stage, this percentage reaches more that 90%, which supposes a sequential number of steps that is less than the 0.5% of the total amount of voxels for any random image. For the 1/2 pairs results are even better: almost all couples can be canceled in parallel.

Finally, a third set of tests were performed for three real binary 3D medical images. Clinical Micro Computer Tomography Images of trabecular bones (obtained by the ETH, Zurich) were selected because of their usually complex topology, consisting of many cavities and tunnels (see Table 1, rows 9–12). Results are similar to that of random images, that is, around a 90% of 0/1 pair transports and around 97% of 1/2 pair transports can be done in a fully parallel manner just in four iterations for the first pairs and in one iteration for the second ones. Because natural images are usually simpler than the random ones, less transports are necessary for them. In fact, the sequential number of steps for this set of medical images is around ten times inferior (less than the 0.05% of the total amount of voxels).

In conclusion, a new parallel algorithm for computing a HSF of a 3D digital object is designed and implemented. It has been demonstrated that its time complexity order is almost logarithmic (remaining only a linear term less than the 0.5% of the total amount of voxels even for random images). Several aspects to progress in a near future are: (a) To further improve the efficiency of some procedures of the algorithm: activation of processing units, crack transport, etc.; (b) To improve the results in object recognition of homology-based features via the definition of a “region-adjacency-graph” of the HSF and the proposal of new topological-based features; (c) To implement a 4D version of the algorithm for topological experimentation in this context.