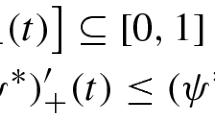Abstract
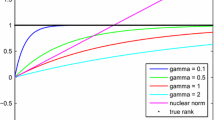
We propose Ky Fan 2-k-norm-based models for the non-convex low-rank matrix recovery problem. A general difference of convex algorithm (DCA) is developed to solve these models. Numerical results show that the proposed models achieve high recoverability rates.
This work is partially supported by the Alan Turing Fellowship of the first author.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Argyriou, A., Foygel, R., Srebro, N.: Sparse prediction with the \(k\)-support norm. In: NIPS, pp. 1466–1474 (2012)
Bhatia, R.: Matrix Analysis, Graduate Texts in Mathematics, vol. 169. Springer, New York (1997)
Candès, E.J., Recht, B.: Exact matrix completion via convex optimization. Found. Comput. Math. 9(6), 717–772 (2009)
Candès, E.J., Tao, T.: Decoding by linear programming. IEEE Trans. Inf. Theory 51(12), 4203–4215 (2005)
Doan, X.V., Vavasis, S.: Finding the largest low-rank clusters with Ky Fan \(2\)-\(k\)-norm and \(\ell _1\)-norm. SIAM J. Optim. 26(1), 274–312 (2016)
Giraud, C.: Low rank multivariate regression. Electron. J. Stat. 5, 775–799 (2011)
Jacob, L., Bach, F., Vert, J.P.: Clustered multi-task learning: a convex formulation. NIPS 21, 745–752 (2009)
Ma, T.H., Lou, Y., Huang, T.Z.: Truncated \(\ell _{1-2}\) models for sparse recovery and rank minimization. SIAM J. Imaging Sci. 10(3), 1346–1380 (2017)
Pham, D.T., Hoai An, L.T.: Convex analysis approach to dc programming: theory, algorithms and applications. Acta Mathematica Vietnamica 22(1), 289–355 (1997)
Pham, D.T., Hoai An, L.T.: A dc optimization algorithm for solving the trust-region subproblem. SIAM J. Optim. 8(2), 476–505 (1998)
Recht, B., Fazel, M., Parrilo, P.: Guaranteed minimum-rank solutions of linear matrix equations via nuclear norm minimization. SIAM Rev. 52(3), 471–501 (2010)
Toh, K.C., Todd, M.J., Tütüncü, R.H.: SDPT3-a MATLAB software package for semidefinite programming, version 1.3. Optim. Methods Softw. 11(1–4), 545–581 (1999)
Yin, P., Esser, E., Xin, J.: Ratio and difference of \(\ell _1\) and \(\ell _2\) norms and sparse representation with coherent dictionaries. Commun. Inf. Syst. 14(2), 87–109 (2014)
Yin, P., Lou, Y., He, Q., Xin, J.: Minimization of \(\ell _1-\ell _2\) for compressed sensing. SIAM J. Sci. Comput. 37(1), A536–A563 (2015)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Doan, X.V., Vavasis, S. (2020). Low-Rank Matrix Recovery with Ky Fan 2-k-Norm. In: Le Thi, H., Le, H., Pham Dinh, T. (eds) Optimization of Complex Systems: Theory, Models, Algorithms and Applications. WCGO 2019. Advances in Intelligent Systems and Computing, vol 991. Springer, Cham. https://doi.org/10.1007/978-3-030-21803-4_32
Download citation
DOI: https://doi.org/10.1007/978-3-030-21803-4_32
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-21802-7
Online ISBN: 978-3-030-21803-4
eBook Packages: Intelligent Technologies and RoboticsIntelligent Technologies and Robotics (R0)