Efficient Computation of Sparse Higher Derivative Tensors

Abstract

The computation of higher derivatives tensors is expensive even for adjoint algorithmic differentiation methods. In this work we introduce methods to exploit the symmetry and the sparsity structure of higher derivatives to considerably improve the efficiency of their computation. The proposed methods apply coloring algorithms to two-dimensional compressed slices of the derivative tensors. The presented work is a step towards feasibility of higher-order methods which might benefit numerical simulations in numerous applications of computational science and engineering.

Supported by the DFG project “Aachen dynamic optimization environment” funded by the German Research Foundation.

1 Introduction

The preferred numerical method to compute derivatives of a computer program is Algorithmic Differentiation (AD) [1, 2]. This technique produces exact derivatives with machine accuracy up to an arbitrary order by exploiting elemental symbolic differentiation rules and the chain rule. AD distinguishes between two basic modes: the forward mode and the reverse mode. The forward mode builds a directional derivative (also: tangent) code for the computation of Jacobians at a cost proportional to the number of input parameters. Similarly, the reverse mode builds an adjoint version of the program but it can compute the Jacobian at a cost that is proportional to the number of outputs. For that reason, the adjoint method is advantageous for problems with a small set of output parameters, as it occurs frequently in many fields of computational science and engineering.

For some methods second or even higher derivatives are required. In [3] it was already shown that Halley-methods using third derivatives are competitive to the Newton’s method. The use of higher-order Greeks to evaluate financial options is discussed in [4]. The moments method approximates moments of a function by propagating uncertainties [5, 6]. To improve the accuracy of the approximated moments higher-order terms in the Taylor series that require higher derivatives need to be involved. The method has been applied to robust design optimization using third derivatives [7].

One possibility to obtain higher derivatives is to propagate Taylor series [8]. Another is to reapply the AD modes to an already differentiated program [2]. In [9] it is shown that computing a projection of the third derivative is proportional to the cost of calculating the whole Hessian. Nevertheless, the computation of higher derivatives is expensive even for adjoint algorithmic differentiation methods.

In this paper, we focus on the exploitation of symmetry and investigate the case where the d-th derivative tensor is considered sparse. Besides the application of coloring techniques for solving linear systems [10] these can be used to exploit the sparsity of Jacobian and Hessian matrices. The general idea is to assign the same color to those columns (or rows) of the corresponding matrix that are structurally orthogonal, thus they can be computed at the same time. In [11] a comprehensive summary of coloring techniques is given. We designed procedures to make solutions of the coloring problem applicable to the computation of third and higher derivative tensors. Due to symmetries of these tensors the colors obtained by a Hessian coloring can be applied multiple times. Furthermore, these colors can be used for a compression of higher derivative tensors to perform a coloring on the compressed two-dimensional slices of the tensor. We call this approach recursive coloring.

For the computation of sparse fourth derivatives we introduced three different approaches: The first is to use the colors of the Hessian three times. The second is to use the colors of the Hessian once to compress the third derivative, reapply the coloring algorithms to the two-dimensional slices of the compressed three-tensor and use the colors of the third derivative twice. The third is to use the colors of the Hessian and the third derivative slice to compress the fourth derivative and again color each two-dimensional slice. We generated random sparse polynomials for matrices from the Matrix Market collection [12] for the computation of sparse fourth derivative tensors to evaluate the efficiency of the three approaches.

The paper is organized as follows: In Sect. 2 there is a brief introduction to AD. Section 3 gives an overview of coloring techniques to exploit the sparsity of Hessian matrices. Subsequently in Sect. 4 we describe the procedures to exploit sparsity for third and higher derivatives. A description of the test cases and their implementation can be found in Sect. 5. Furthermore, this section provides numerical results to compare the introduced procedures. The last section gives a conclusion and an outlook.

2 Algorithmic Differentiation in a Nutshell

AD is a technique that transforms a primal function or primal code by using the chain rule to compute additionally to the function value the derivative of that function with respect to a given set of input (and intermediate) variables. For simplicity and w.l.o.g. we will only consider multivariate scalar functions. Thus the given primal code has a set of n inputs $\mathbf {x}$ and a single output y.

$$\begin{aligned} f:\mathbb {R}^{n} \rightarrow \mathbb {R},\quad y =f\left( \mathbf {x}\right) \end{aligned}$$

Furthermore, we assume that we are interested in the derivatives of the output variable with respect to all input variables. The first derivative of these functions is the gradient $\nabla f(\mathbf {x}) \in \mathbb {R}^{n}$, the second derivative is the Hessian $\nabla ^2 f(\mathbf {x}) \in \mathbb {R}^{n\times n},$ and the third derivative is the three-tensor $\nabla ^3 f(\mathbf {x}) \in \mathbb {R}^{n\times n\times n}.$ In this paper a two-dimensional subspace of a tensor will be referred as a slice.

Schwarz’s theorem says that the Hessian is symmetric if f has continuous second partial derivatives

$$\begin{aligned} \frac{\partial ^2 y}{\partial x_j \partial x_k} = \frac{\partial ^2 y}{\partial x_k \partial x_j}. \end{aligned}$$

(1)

This generalizes to third and higher derivatives. Thus, a derivative tensor of order d has only $\left( {\begin{array}{c}n+d-1\\ d\end{array}}\right)$ structurally distinct elements.

AD is applicable if f and its corresponding implementation are locally differentiable up to the required order. The two basic modes are introduced in the following sections.

2.1 Tangent Mode AD

The tangent model can be simply derived by differentiating the function dependence. In Einstein notation this yields

$$\begin{aligned} y^{(1)} = \frac{\partial y}{\partial x_j} x_j^{(1)}. \end{aligned}$$

The notation implies summation over all the values of $j=0,\ldots ,n-1$. The superscript $^{(1)}$ stands for the tangent of the variable [2]. This approach can be interpreted as an inner product of the gradient $\nabla f(\mathbf {x}) \in \mathbb {R}^{n}$ and the tangent $\mathbf {x}^{(1)}$ as

$$\begin{aligned} y^{(1)} = f^{(1)}(\mathbf {x},\mathbf {x}^{(1)}) = \nabla f(\mathbf {x}) \cdot \mathbf {x}^{(1)}. \end{aligned}$$

(2)

For each evaluation with $\mathbf {x}^{(1)}$ set to the i-th Cartesian basis vector $\mathbf {e}_i$ in $\mathbb {R}^n$ (also called seeding), an entry of the gradient can be extracted from $y^{(1)}$ (also called harvesting). To get all entries of the gradient by using this model, n evaluations are required which is proportional to the number of input variables. The costs of this method are similar to the costs of a finite difference approximation but AD methods are accurate up to machine precision.

2.2 Adjoint Mode AD

The adjoint mode is also called reverse mode, due to the reverse computation of the adjoints compared to the computation of the values. Therefore, a data-flow reversal of the program is required, to store additional information on the computation (e.g. partial derivatives) [13], which potentially leads to high memory requirements.

Again following [2], first-order adjoints are denoted with a subscript $_{(1)}$

$$\begin{aligned} x_{(1),j} = \frac{\partial y}{\partial x_j} y_{(1)}. \end{aligned}$$

This equation is computed for each $j=0,\ldots ,n-1$.

Reverse mode yields a product of the gradient with the adjoint $y_{(1)}$

$$\begin{aligned} \mathbf {x}_{(1)} = f_{(1)}(\mathbf {x},y_{(1)}) = y_{(1)} \cdot \nabla f(\mathbf {x}). \end{aligned}$$

(3)

By setting $y_{(1)} = 1$ the resulting $\mathbf {x}_{(1)}$ contains all entries of the gradient. A single adjoint computation is required.

2.3 Higher Derivatives

One possibility to obtain second derivatives is to nest the proposed AD modes. Hence there are four combinations to compute second derivatives. The tangent-over-tangent model result from the application of tangent mode to the first-order tangent model in (2):

$$\begin{aligned} \begin{aligned} y^{(1,2)} = f^{(1,2)}(\mathbf {x},\mathbf {x}^{(1)}, \mathbf {x}^{(2)}) = \frac{\partial ^2 y}{\partial x_j\partial x_k} x_j^{(1)} x_k^{(2)}. \end{aligned} \end{aligned}$$

By seeding the Cartesian basis of $\mathbb {R}^n$ for the tangents $\mathbf {x}^{(1)}$ and $\mathbf {x}^{(2)}$ independently the entries of the Hessian can be computed with $n^2$ evaluations of $f^{(1,2)}$. The other three methods apply the adjoint mode at least once and thus their computational complexity is different to the pure tangent model. To obtain the whole Hessian a second-order adjoint model needs to be evaluated n times.

Applying the tangent mode to (3) yields the second-order adjoint model

$$\begin{aligned} x_{(1),k}^{(2)} = f^{(2)}_{(1),k}(\mathbf {x}, \mathbf {x}^{(2)},y_{(1)}) = \frac{\partial ^2 y}{\partial x_k\partial x_j} x_j^{(2)} y_{(1)}\ . \end{aligned}$$

(4)

These models are simplified versions of the complete second-order models by setting mixed terms to zero. Detailed derivations can be found in [1] and [2].

Recursively applying the two basic modes yields even higher derivative models. As an example the simplified third-order adjoint model via tangent-over-tangent-over-adjoint can be written as

$$\begin{aligned} x_{(1),l}^{(2,3)} = f^{(2,3)}_{(1),l}(\mathbf {x}, \mathbf {x}^{(2)}, \mathbf {x}^{(3)}, y_{(1)}) = \frac{\partial ^3 y}{\partial x_l\partial x_k\partial x_j} x_j^{(2)} x_k^{(3)} y_{(1)}. \end{aligned}$$

(5)

Instead of seeding all combinations of Cartesian basis vector for both tangents which requires $n^2$ evaluations of $f^{(2,3)}_{(1)}$ we could exploit symmetry and evaluate the adjoint model only for those combinations of directional derivatives that fulfill $n \ge i_2 \ge \ldots \ge i_{d-1} \ge i_d \ge 1$. Thus, the tangents $\mathbf {x}^{(j)}$ are set to $\mathbf {e}_{i_j}$ for ${2 \le j \le d}$. which results in $\left( {\begin{array}{c}n+d-2\\ d-1\end{array}}\right)$ evaluations of the d-th order adjoint model.

3 Coloring Techniques

For the computation of higher derivatives it is indispensable to exploit the sparsity and symmetry of the particular matrices or tensors due to the expenses that come along with their computation. We aim for a reduction of the number of projections that are needed for the computation of the sparse derivative. In [14, 15] it is shown that the symmetric graph coloring problems considered in this section are equivalent to a matrix partitioning problem and can be used to enable the determination of the corresponding derivative matrices.

Coloring techniques can be used to exploit sparsity of Jacobian and Hessian matrices [11]. The general idea is to identify columns (or rows) of the corresponding matrix that can be computed at the same time and assign the same color to these columns.

Definition 1

We define $\varvec{\mathcal {C}}_j$ to denote the set that contains the indices of all columns belonging to color j. These sets are grouped in a set of sets $\varvec{\mathcal {C}}^d$ for the d-th derivative. $\varvec{\mathcal {C}}^d$ can be used to compute a compressed derivative by seeding $\sum _{j\in \varvec{\mathcal {C}}_k}\mathbf {e}_j$ for each color k instead of $\mathbf {e}_j$ for each column.

In the following we outline the difference between direct and indirect coloring heuristics for Hessian matrices. For the proposed heuristics we assume multivariate scalar functions ${f:\mathbb {R}^{n} \rightarrow \mathbb {R}}$. Furthermore, we assume their sparsity patterns of all derivatives to be known.

Definition 2

The sparsity pattern of the d-th derivative is a set that contains the (multi-)indices of those elements that are non-zero. It is denoted by $\varvec{\mathcal {P}}^d$.

The detection of sparsity patterns is out of the scope of this paper. For further reading about sparsity pattern detection see for example [16, 17].

3.1 Hessian Coloring with Direct Recovery

A direct approach to find a suitable Hessian coloring considering symmetry of the Hessian (1) is the so called star coloring. This heuristic ensures that each element of the Hessian is computed at least once and can be directly extracted from the computed derivative projections. Star coloring uses an adjacency graph where each node belongs to a column (or row). Each non-zero element $\frac{\partial ^2 y}{\partial x_j \partial x_k}$ with $(j,k) \in \varvec{\mathcal {P}}^2$ in the matrix is an edge connecting node j and k in the graph. Then, a distance-1 coloring is applied to the graph in that the same color cannot be assigned to adjacent nodes. Furthermore, there is an additional condition that every path of length four uses at least three colors. The nodes and thus the columns of the Hessian with the same color can be computed simultaneously.

3.2 Hessian Coloring with Indirect Recovery

Another heuristic described in [11] is acyclic coloring that also applies distance-1 coloring to the adjacency graph. This coloring technique has the additional condition that each cycle in the graph needs at least three distinct colors. Since it might assign the same color to columns that are not structurally orthogonal, the derivative matrix can be compressed even more. Nevertheless, a recovery of these non-zero elements implies the solution of a system of linear equations.

Both methods for Hessian coloring reduce the number of required derivative projections from n to $|\varvec{\mathcal {C}}^2|$.

4 Computation of Sparse Derivative Tensors

In this section, we show how to use coloring heuristics introduced in Sect. 3 to obtain sparse higher derivative tensors efficiently. Section 4.1 focuses on the reapplication of colors for higher derivatives. In Sect. 4.2 a recursive coloring approach for the computation of higher derivatives is described. After that, we propose the incomplete recursive coloring in Sect. 4.3. We will use the higher-order adjoint models from Sect. 2.3, that is (5) for third derivatives.

The proposed algorithms assume multivariate scalar functions ${f:\mathbb {R}^{n} \rightarrow \mathbb {R}}$ for simplicity. For the more general case of multivariate vector functions the algorithms can be applied to each output variable individually. It is also possible to combine the proposed approaches with Jacobian coloring for vector functions to make their derivative computation more efficient, but this is future work.

We will illustrate the algorithms in this section for

$$\begin{aligned} f(\mathbf {x}) = \sum _{i=0}^{n-1} x_i^3 + \sum _{i=1}^{n-2} x_{i-1} \cdot x_i \cdot x_{i+1}, \end{aligned}$$

(6)

with $n=6$. The sparsity pattern of the Hessian and the corresponding adjacency graph are visualized in Fig. 1. The colors in this figure are a solution for the symmetric graph coloring problem obtained by acyclic coloring.

Fig. 1.

Sparsity pattern of the Hessian (left) and the corresponding adjacency graph (right) with colors obtained by acyclic coloring for the function from (6) (Color figure online)

4.1 Reapplication of Colors

In [3] a so called induced sparsity of the third derivative was introduced where

$$\begin{aligned} \left( \nabla ^2f_{jk}=0\ \vee \ \nabla ^2f_{jl}=0\ \vee \ \nabla ^2f_{kl}=0\right) \quad \Rightarrow \quad \nabla ^3f_{jkl}=0. \end{aligned}$$

(7)

Definition 3

We call a third-order tensor induced sparse if only those elements that fulfill (7) have zero entries. The same can be generalized to any order $d \ge 2$: a d-th-order tensor is called induced sparse if only those elements of the tensor are zero that are induced by a zero in the $(d-1)$-th derivative. The induced sparsity pattern of the d-th derivative is denoted as $\tilde{\varvec{\mathcal {P}}}^d$.

We extended the concept of induced sparsity to show that the colors obtained by a Hessian coloring can be used for the higher derivative computation.

Lemma 1

Every solution $\varvec{\mathcal {C}}$ of the coloring problem for a symmetric matrix $A\in \mathbb {R}^{n\times n}$ with sparsity pattern $\varvec{\mathcal {P}}_A$ is also valid for a symmetric matrix $B\in \mathbb {R}^{n\times n}$ with sparsity pattern $\varvec{\mathcal {P}}_B$ if $\varvec{\mathcal {P}}_B \subseteq \varvec{\mathcal {P}}_A$.

Proof

In case of $\varvec{\mathcal {P}}_B \subseteq \varvec{\mathcal {P}}_A$ we can consider a matrix $A'$ with the same sparsity pattern as A as a composition of matrix B with its values at $(j,k) \in \varvec{\mathcal {P}}_B$, numerical zeros at $(j,k) \in \varvec{\mathcal {P}}_A \backslash \varvec{\mathcal {P}}_B$ and structural zeros at $(j,k) \notin \varvec{\mathcal {P}}_A$. The coloring result $\varvec{\mathcal {C}}$ obtained for A can be used to determine matrix $A'$ and thus B beside the numerical zeros. $\blacksquare$

Theorem 1

A solution $\varvec{\mathcal {C}}^2$ of the coloring problem for a Hessian matrix can be used for seeding the $(d-1)$ tangents of a d-th-order adjoint model to compute the d-th derivative tensors for $d \ge 2$.

Proof

Mathematical induction can be used to prove that Theorem 1 holds for all natural numbers $d \ge 2$.

Basis: Since [14, 15] showed that the symmetric graph coloring problems can be transformed to matrix partitioning problems, colors $\varvec{\mathcal {C}}^2$ obtained for the coloring problem can be used as seed vectors for the tangent of the second-order adjoint model (4). Thus, Theorem 1 holds for $d=2$.

Inductive Step: Given that Theorem 1 holds for the $(d-1)$-th derivative, we can apply the Hessian colors to compress this derivative at least $d-2$ times. We need to show that the Hessian colors $\varvec{\mathcal {C}}^2$ can be used $d-1$ times for the d-th derivative.

The induced sparsity from (7) holds for any order $d \ge 2$ and the sparsity pattern of each slice $\tilde{\varvec{\mathcal {P}}}^d_{i_j}$ is a subset of the sparsity pattern of the $(d-1)$-th derivative $\varvec{\mathcal {P}}^{d-1}$, where $i_j$ is the index for the direction of tangent $\mathbf {x}^{(j)}$. Furthermore, the induced pattern is an overestimation of the actual sparsity pattern $\varvec{\mathcal {P}}^d_{i_j}$ which yields

$$\begin{aligned} \varvec{\mathcal {P}}^d_{i_j} \subseteq \tilde{\varvec{\mathcal {P}}}^d_{i_j} \subseteq \varvec{\mathcal {P}}^{d-1} \qquad \text {for} \qquad 0 \le {i_j} \le n-1\ , \end{aligned}$$

(8)

with $2 \le j \le d$.

Lemma 1 is applicable since (8) holds such that the coloring results used to compute the $(d-1)$-th derivative can also be used for the computation of the d-th derivative. This includes that the Hessian colors can be applied for the first $d-2$ tangents due to the assumption that the theorem holds for $d-1$. Seeding these tangents yields $\mathbf {x}^{(j)} = \sum _{k\in \varvec{\mathcal {C}}^2_{i_j}}\mathbf {e}_k$ for $2\le j\le d-1$. Thus, it remains to show that $\varvec{\mathcal {C}}^2$ can also be applied to the last tangent $\mathbf {x}^{(d)}$.

Using the Hessian colors for the $d-2$ tangents leads to a compression of the d-th-order tensor which is a projection of the derivative tensor in direction of the colors

$$\begin{aligned} \sum _{k_2\in \varvec{\mathcal {C}}^2_{i_2}}\ldots \sum _{k_{d-1}\in \varvec{\mathcal {C}}^2_{i_{d-1}}}\nabla ^d f_{k_2,\ldots k_{d-1}} \end{aligned}$$

(9)

and reduces the size of the corresponding tangent directions $i_j$ with $2 \le j \le d-1$ from n to $|\varvec{\mathcal {C}}^2|$. For each combination of the directions we will receive a two-dimensional slice of the tensor of size $n\times n$.

Again (8) shows that the sparsity pattern of each of these slices is still a subset of the sparsity pattern of the $(d-1)$-th derivative

$$\begin{aligned} \bigcup _{k\in \varvec{\mathcal {C}}_{i_d}}\varvec{\mathcal {P}}^d_{k} \subseteq \varvec{\mathcal {P}}^{d-1} \quad \text {for}\quad 0 \le i_d \le |\varvec{\mathcal {C}}|-1. \end{aligned}$$

(10)

Recursively applying (10) for $(d-2)$ tangents yields

$$\begin{aligned} \bigcup _{k_2\in \varvec{\mathcal {C}}^2_{i_2}}\ldots \bigcup _{k_{d-1}\in \varvec{\mathcal {C}}^2_{i_{d-1}}}\varvec{\mathcal {P}}^d_{k_2,\ldots k_{d-1}} \subseteq \varvec{\mathcal {P}}^2 \quad \text {for}\ \ 0 \le i_j \le |\varvec{\mathcal {C}}^2|-1,\ \ 2 \le j \le d-1. \end{aligned}$$

Hence, due to Lemma 1 $\varvec{\mathcal {C}}^2$ can also be used to seed tangent $\mathbf {x}^{(d)}$. Thus, with the inductive step, we have shown that the Hessian colors $\varvec{\mathcal {C}}^2$ are $(d-1)$ times applicable for the computation of the d-th derivative. $\blacksquare$

Applying the Hessian colors for all tangents requires $|\varvec{\mathcal {C}}^2|^{d-1}$ model evaluations of the d-th-order adjoint model to compute the whole d-th derivative tensor.

Example 1

The induced sparsity pattern of the third derivative of (6) is shown in Fig. 2. It can be seen, that the actual sparsity pattern (gray) is a subset of the induced sparsity pattern (striped).

Using the Hessian colors from Fig. 1 for the first tangent results in the compressed derivative tensor visualized in Fig. 3 (left). The sparsity pattern of each slice of the compressed tensor is (a subset of) the Hessian sparsity pattern. Thus, the Hessian colors are applied again.

Fig. 2.

Induced (striped) and actual (gray) sparsity pattern of the third derivative

Fig. 3.

Sparsity pattern of the third derivative projections by using Hessian colors of function (6) with resulting colorings for reapplication of Hessian colors (left) and recursive coloring results (right) (Color figure online)

4.2 Recursive Coloring

Since the actual sparsity patterns of the higher derivatives are assumed to be known, this information should be used to design more efficient algorithms.

Definition 4

Recursive coloring is defined as a technique that recursively solves the symmetric graph coloring problem for two-dimensional slices (fixing the compressed directions) of a compressed d-th derivative tensor (9) and to use the solution of this problem for seeding tangent $\mathbf {x}^{(d)}$. The other tangents need to be set previously for the compression.

Algorithm 1 describes the procedure for a d-th derivatives. To compress the tensor of order d the coloring results of all lower derivatives are required. These colors are computed by the recursive call in line 3. Note that the variable $\mathbf {C}^{d-1}$ is a list that contains all coloring results $\varvec{\mathcal {C}}^{d-1}_L$ as a set of sets. The subscript L of $\varvec{\mathcal {C}}^{d}_L$ is the list of the $d-2$ tangent directions for the compression of the d-th derivative tensor that led to the coloring. In line 6 the k-th color of $\varvec{\mathcal {C}}^{d-1}_L$ is attached to L. This new list is used in line 7 to compress the tensor and to obtain the coloring for one slice of the compressed d-th-order tensor by solving the coloring problem for a symmetric matrix. After that, the new colors are attached to $\mathbf {C}^d$.

The following lemma will be used to show that the recursive coloring is at least as good as the reapplication of colors.

Lemma 2

The number of colors of the optimal solution $\varvec{\mathcal {C}}^A$ of the coloring problem for a symmetric matrix $A\in \mathbb {R}^{n\times n}$ with sparsity pattern $\varvec{\mathcal {P}}_A$ is larger than that for a symmetric matrix $B\in \mathbb {R}^{n\times n}$ with sparsity pattern $\varvec{\mathcal {P}}_B$ if $\varvec{\mathcal {P}}_B \subseteq \varvec{\mathcal {P}}_A$, such that $|\varvec{\mathcal {C}}^B| \le |\varvec{\mathcal {C}}^A|$.

Proof

In a proof by contradiction we assume the optimal coloring results $|\varvec{\mathcal {C}}^B| > |\varvec{\mathcal {C}}^A|$. Since $\varvec{\mathcal {P}}_B \subseteq \varvec{\mathcal {P}}_A$ we can apply Lemma 1 such that $\varvec{\mathcal {C}}^A$ is also a coloring for B, which implies that $\varvec{\mathcal {C}}^B$ was not optimal. Thus, the assumption was wrong. $\blacksquare$

Theorem 2

The optimal number of adjoint model evaluations obtained with a recursive coloring is less than or equal to the optimal number of adjoint model evaluations resulting from the reapplication of colors.

Proof

Assuming that both approaches have the same compression for the first $d-2$ tangents, it is necessary to show that the number of adjoint model evaluations for recursive coloring is less than those of the reapplication of colors

$$\begin{aligned} \sum _{\varvec{\mathcal {C}}^{d-1}_L \in \mathbf {C}^{d-1}} \sum _{k \in \varvec{\mathcal {C}}^{d-1}_L} |\varvec{\mathcal {C}}^d_{\{L,k\}}| \quad \le \quad \sum _{\varvec{\mathcal {C}}^{d-1}_L \in \mathbf {C}^{d-1}} \sum _{k \in \varvec{\mathcal {C}}^{d-1}_L} |\varvec{\mathcal {C}}^{d-1}_L| \quad , \end{aligned}$$

(11)

where $\mathbf {C}^{d-1}$ is the list of coloring results for the $(d-1)$-th derivative and L contains those directions that are used for the compression of this derivative.

Since (10) holds for any coloring $|\varvec{\mathcal {C}}|$ we can apply Lemma 2 to show

$$\begin{aligned} |\varvec{\mathcal {C}}^d_{\{L, k\}}| \le |\varvec{\mathcal {C}}^{d-1}_L|\quad \text {for}\quad k \in \varvec{\mathcal {C}}_L^{d-1}\ , \end{aligned}$$

(12)

such that the minimal number of colors obtained for two-dimensional slices in $\mathbb {R}^{n\times n}$ of the compressed d-th derivative tensor is less than or equal to those used for the compression. Thus, (12) directly yields (11). $\blacksquare$

By using heuristics to obtain a solution of the coloring problems, it might be that the solution $\varvec{\mathcal {C}}^d_{\{L, k\}}$ is worse than $\varvec{\mathcal {C}}^{d-1}_L$ for some k. In that case the algorithm should select the colors used for tangent $\mathbf {x}^{(d-1)}$ by setting $\varvec{\mathcal {C}}^d_{\{L, k\}} = \varvec{\mathcal {C}}^{d-1}_L$.

The resultant seeding can be stored in a tree structure. The seed of the adjoint is stored in the root of the tree, which has $|\varvec{\mathcal {C}}^2|$ children. These nodes with depth 1 contain the first tangent directions that correspond to the Hessian colors. Analogous, the nodes with depth 2 store the coloring results of the compressed third derivative. In general, the compression is done by the information stored in all nodes on the path connecting that node with the root. In case of a node with depth 2, this will be only the direction that is stored in its parent node. To obtain the complete higher derivative each path from a leaf to the root needs to be used as a seeding for the adjoint model.

The list L in Algorithm 1 does not need to be stored explicitly, because this information is already available in the tree structure. Depending on the coloring results the tree does not need to be balanced. Furthermore, due to (10) we know that each node has no more children than its parent node.

Fig. 4.

Seeding trees for computing the third derivative tensor of the example for the reapplication of Hessian colors (left) and the recursive coloring (right)

Example 2

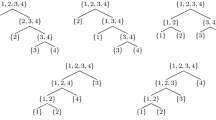
The results of the recursive coloring are illustrated in Fig. 3 (right) for the example function. After the compression with the first tangent $x^{(2)} = \varvec{\mathcal {C}}^2_{i_2}$ the resulting slices are colored again. In case of $i_j = 0$ the resulting coloring is $\{\{0,2,3,5\},\{1,4\}\}$. The seeding trees for both approaches, the reapplication of colors and the recursive coloring are shown in Fig. 4.

4.3 Incomplete Recursive Coloring

The incomplete recursive coloring is an approach that combines the reapplication of colors from Sect. 4.1 and the recursive coloring from Sect. 4.2. Instead of applying a full recursive coloring, the recursion can be stopped on any level and the computed colors can be reapplied for all tangents that belong to higher derivatives. This is possible due to Lemma 1 and (8). The additional check if the recursive coloring should be stopped in line 7 of Algorithm 2 is the main modification. In that case the previously computed colors are reused (line 10) and the list in the subscript needs to be updated.

Definition 5

We call an incomplete recursive coloring a d-th-order approach if it uses colorings of derivatives up to d-th-order. The approach of using the Hessian colors for all tangents from Sect. 4.1 is an incomplete recursive coloring of second order.

5 Experiments and Results

In this section we compare the different coloring approaches presented in Sect. 4 for a computation of a fourth derivative tensor. For evaluating the approaches we use a tool that creates sparse fourth-order polynomials from sparsity patterns. It is stored in a data structure that is an extension of the compressed tube storage [3] for super-symmetric induced four-tensors. The tool takes the sparsity ratio of the third $\rho _3$ and the fourth $\rho _4$ derivative.

Definition 6

We define the sparsity ratio $\rho _d$ to describe the ratio of non-zero elements in the d-th derivative compared to the number of elements that are induced by the $(d-1)$-th derivative. Given that the gradient is dense, $\rho _2$ is the ratio of non-zero elements to distinct elements in the Hessian.

Due to the fact that the proposed approaches only apply colorings to two-dimensional (sub-)spaces of the derivative tensors, coloring algorithms implemented in ColPack [18] can be used. Particularly, we use the acyclic coloring algorithm with indirect recovery to obtain the expected colors.

In a first set of tests we want to investigate the efficiency of the second-order approach compared to an approach disregarding the sparsity (see Sect. 2.3).

Table 1. Selected matrices from [12] with the ratio of projections required for the second-order approach to a computation disregarding sparsity

Fig. 5.

Number of projections of the three coloring approaches for the nos4 example (left) and for a set of test cases from [12] and induced sparsity (right) (Color figure online)

After that, we vary the parameters for the sparsity of the higher derivative tensors $\rho _3$ and $\rho _4$. In case of $0< \rho _3 < 1$ or $0< \rho _4 < 1$ the sparsity patterns of the higher derivatives are generated randomly such that we perform 1000 computations for each of the parameter combinations and average the results. As a test case we selected the nos4 matrix from [12].

In a third test, we compute the derivatives of polynomials generated from several matrices from the database. A selection of these matrices is listed in Table 1, in which the first column is the name in the database, the second is the size and the third is the sparsity ratio $\rho _2$ of the matrix. For this test we assume that the higher derivatives are induced sparse ($\rho _3=1$ and $\rho _4=1$) which will result in a somehow worst-case estimation of the efficiency of the third- and fourth-order approaches. This test only requires the Hessian sparsity pattern.

5.1 Numerical Results

The results for the efficiency of the second-order approach is given in the last column of Table 1. It can be seen that this approach becomes more efficient if the matrices become sparser. The number of derivative projections required for the second-order approach are less than 7% of those required with the symmetric approach disregarding sparsity.

Figure 5 (left) visualizes the results for the second tests. The black line shows the number of seeds that are required for the Hessian coloring approach. It is constant because the Hessian coloring is independent on the sparsity of the higher derivatives. The red line shows the incomplete recursive coloring up to third order, which means that the colors of the compressed third derivative slices are computed. The blue lines stand for the full recursive coloring. These lines are isolines with a constant parameter for the sparsity of the fourth derivative.

It can be seen that the recursive colorings up to third and fourth order become more efficient the sparser the corresponding derivatives are. In the special case of $\rho _3 = 0$ or $\rho _4=0$ the number of adjoint model evaluations is zero for the approaches that use these parameters. In the induced sparse case, the incomplete recursive coloring up to third order still reduces the number of required projections to 47.2% of the Hessian coloring approach, while the fully recursive approach is even better with 38.9%. So even in the case where the higher derivatives are as dense as possible dependent on the sparsity of the Hessian, the recursive approaches yield good savings in terms of adjoint model evaluations.

Similar results can be observed for the other test matrices. Figure 5 (right) shows the results for the matrices from Table 1. Again the black bar denotes the second-order approach, the red bar stands for the incomplete third-order recursive coloring and the blue bar shows the full recursive coloring approach. The average savings compared to the second-order approach are 75.9% for the incomplete recursive coloring and 68.5% for the full recursive coloring only considering test cases with more than a single color for the Hessian matrix. In the case of third and fourth derivative that are sparser than the induced sparsity the recursive coloring approaches become more efficient.

6 Conclusion and Outlook

In this paper we have introduced procedures to make coloring techniques applicable for the computation of higher derivative tensors. We proposed two basic concepts to achieve this: application of previous computed colors and recursive coloring. By combining both concepts we came up with the incomplete recursive coloring. Depending on how much sparsity information is available the recursion depth of this approach can be adjusted.

The results show that even in the case where only the Hessian sparsity is known the savings compared to an approach disregarding sparsity are significant. Including higher sparsity information increases these savings further. Assuming that the costs of the coloring is considerably lower than an adjoint evaluation, additional colorings of the compressed slices can be accepted. Furthermore, the (incomplete) recursive coloring of the higher derivative tensors can be considered to be done in compile-time to build up the seeding tree. This seeding tree can be used multiple times in the execution to obtain derivatives at various points.

In the future, we intend to provide a software package making the (incomplete) recursive coloring setup available to efficiently generate seeding trees for the computation of higher derivatives with the most common AD tools. For the parallelization of the proposed algorithms it is necessary to find a suitable load balancing. Another interesting future study should consider direct coloring methods for higher derivative tensors. We expect that direct coloring further decreases the number of required projections and thus the costs of the higher derivative computation.