Keywords

1 Introduction

Recently, a tilt-rotor plane represented by V-22 Osprey has become to gain attention, which has features of both a helicopter and a plane. A tilt-rotor plane has a hovering function like a helicopter by turning axes of rotor to vertical during takeoff or landing. On the other hand in flight, it behaves as a reciprocating aircraft by turning axes of rotor to horizontal. These two flight modes are converted by rotating engine nacelles which are mounted to the tip of fixed wings. Although many numerical simulations have been conducted for tilt-rotor plane, most of them are simulations using overset grids because of its complicated shape [1,2,3,4,5]. Thus the geometric conservation law is not satisfied. Moreover, no coupled simulations have been performed between the flow field and the motion of a tilt-rotor plane with operating its flight control surfaces. To achieve a coupled simulation in two flight modes of tilt-rotor plane with high accuracy, we have already proposed a computational technique combining multi-axis sliding mesh approach and the Moving Computational Domain (MCD) method [6]. The MCD method is used to compute movement of a plane and unsteady flows occurred by the motion. The feature of this method is that fluid flows are created by movement itself of a moving object. Specifically, moving wall boundary condition generates flows. Therefore, the method is different from conventional methods that calculate a flow field around a static body placing it in a uniform flow like a wind tunnel. Applying this method to rotation of rotors, flows around them can be computed directly without a decrease in the accuracy caused by simplified computation model. In multi-axis sliding approach, the whole computational domain is divided into multiple domains. The domains are adjacent to each other and one can be embedded in another. Rotation of a body like a rotor and an engine nacelle is achieved by rotating whole computational domain which include them. Some domains can be also embedded in another one. A surface of a domain slides on a boundary between it and its adjacent domain. Physical variables are interpolated on the boundary between two domains.

As previous work, the technique has been adapted to flows around a tilt-rotor plane with three degrees of freedom using a bilaterally symmetric mesh and a symmetric boundary condition. In this paper, six degrees of freedom coupled simulation by using multi-axis sliding mesh approach is presented toward the practical simulation of a tilt-rotor plane. Next, the approach which has already proposed is intended for sliding surface of a flat plane or circular cylinder. In six degrees of freedom computation, it is more useful to be able to handle a spherical sliding surface. Therefore, the approach is improved to be able to deal with free-form surfaces. After some inspections are shown, its validity of the approach is also shown by applying to a flow around a tilt-rotor plane.

2 Numerical Approach

2.1 Governing Equation

As a governing equation, three-dimensional Euler equation is written in the conservation form as follows:

$$ \frac{{\partial \varvec{q}}}{\partial t} + \frac{{\partial \varvec{E}}}{\partial x} + \frac{{\partial \varvec{F}}}{\partial y} + \frac{{\partial \varvec{G}}}{\partial z} = 0, $$
(1)
$$ \varvec{q} = \left[ {\begin{array}{*{20}c} \rho \\ {\rho u} \\ {\rho v} \\ {\rho w} \\ e \\ \end{array} } \right], \varvec{E} = \left[ {\begin{array}{*{20}c} {\rho u} \\ {\rho u^{2} + p} \\ {\rho uv} \\ {\rho uw} \\ {u(e + p)} \\ \end{array} } \right], \varvec{F} = \left[ {\begin{array}{*{20}c} {\rho v} \\ {\rho uv} \\ {\rho v^{2} + p} \\ {\rho vw} \\ {v(e + p)} \\ \end{array} } \right], \varvec{G} = \left[ {\begin{array}{*{20}c} {\rho w} \\ {\rho uw} \\ {\rho vw} \\ {\rho w^{2} + p} \\ {w(e + p)} \\ \end{array} } \right], $$
(2)

where \( \varvec{q} \) is the conserved quantity vector, \( \varvec{E},\varvec{ F},\varvec{ G} \) are the inviscid flux vectors. As unknowns, \( \rho \) is the density, \( u, v, w \) are the x, y, z components of the velocity vector and \( e \) is the total energy per unit volume. The working fluid assumed to be perfect gas, the pressure \( p \) is defined as follows:

$$ p = \left( {\upgamma - 1} \right)\left[ {e - \frac{1}{2}\rho \left( {u^{2} + v^{2} + w^{2} } \right)} \right], $$
(3)

where \( \upgamma \) is the specific heat ratio and taken as 1.4 in this paper.

2.2 Moving Computational Domain Method

In this paper, we tried to simulate a continuous motion of a tilt-rotor plane from takeoff to hovering. To compute such free movement of the body, the Moving Computational Domain (MCD) method [7,8,9,10] was adapted. In the MCD method, a whole computational domain moves together with an object which exists inside the domain shown in Fig. 1. Using the method, that is, it becomes possible to simulate the movement of a tilt-rotor plane in infinite space. This method is one of the moving grid methods because vertices constructing computational domain also move, which is based on the unstructured moving grid finite volume method [11, 12]. In the method, fluxes are evaluated on a control volume in a space-time unified domain (x, y, z, t) to satisfy the geometric conservation law (GCL) [13]. The control volume is four-dimensional volume for three-dimensional flows. Flow variables are defined at the center of the cell in unstructured mesh. The flux vectors are evaluated using the Roe flux difference splitting scheme [14] with MUSCL approach and the Venkatakrishnan limiter [15]. To solve implicit algorithm, the two-stage Runge-Kutta method is adopted.

Fig. 1.
figure 1

Conceptual figure of the MCD

Full size image

2.3 Multi-axis Sliding Mesh Approach

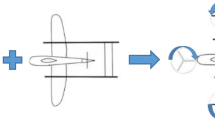
The multi-axis sliding mesh approach is moving grid method to represent local movement of part of an object by dividing the whole computational domain into multiple domains and sliding them. For example, the rotation of propeller is performed by rotating a whole domain containing the propeller. Although the shape of divided sub-domains can be arbitrary unless they interfere with each other, sphere and cylinder is suitable for a rotating body from the aspect of computational cost. Moreover, sub-domains can be nested (see Fig. 2). In this figure, a computational domain 3 is embedded in a computational domain 2. Also, the computational domain 2 is embedded in a computational domain 1. These domains have different axes of rotation respectively which can rotates independently. With combination of movement of sub-domains, new motion is created. For example, as shown in Fig. 3, the vertical motion of an object is achieved by the combination of rotations of two circular domains and a horizontal movement of semicircular domain. The advantage of this approach is that mesh cells don’t strain because all vertices of the mesh move as one. To transform domains, the MCD method is used. The multi-axis sliding mesh approach has a possibility to perform very flexible motion of objects without distorting computational meshes by combining with the MCD.

Fig. 2.
figure 2

Multi-axis sliding mesh approach

Full size image
Fig. 3.
figure 3

Vertical motion by combining circles

Full size image

In the approach, the surface of a computational domain is dealt with a boundary like the wall boundary and outer boundary although there is no physical boundary on the surface, because computational domains have each independent topology. In this paper, the conserved quantity \( \varvec{q}_{\varvec{b}} \) is determined from adjacency relationship between computational domains so as to satisfy the conservation law and interpolated into ghost cells (hereinafter called “sliding boundary condition”).

Let us consider adjacent computational domains A and B to illustrate specific computational step of the sliding boundary condition, shown in Fig. 4. Focusing on the cell i facing the surface within computational domain A, the cell j within computational domain B exists which is adjacent to the cell i across the sliding surface. For the sliding boundary condition, physical values are interpolated based on the area of adjacent face between these cells. To calculate the overlapping area between the faces which may be non-coplanar, the boundary face of cell i is projected onto the boundary face of cell j. The area \( S_{ij} \) of adjacent face between cell i and cell j is defined by the overlapping area between the boundary face of cell i and the projected face. The cell i is generally adjacent to multiple cells within domain B. Thus, as the sliding boundary condition, the interpolated value \( \varvec{q}_{{\varvec{b}i}} \) of the cell i is defined by following equation:

Fig. 4.
figure 4

Adjacent computational domains

Full size image
$$ \varvec{q}_{bi} = \frac{{\sum\limits_{{j{ \in }i}} {\varvec{q}_{j} S_{ij} } }}{{\sum\limits_{j \in i} {S_{ij} } }}, $$
(4)

where \( \varvec{q}_{j} \) is the conserved quantity at the cell j and \( \mathop \sum \nolimits_{j \in i} \) means the summation over cells j which is adjacent to the cell i (Fig. 5).

Fig. 5.
figure 5

Cells facing each other across sliding surface and overlapping area of them used to calculate interpolated value

Full size image

2.4 Coupled Computation

In this paper, the position and rotation of a tilt-rotor plane is automatically determined by the fluid flow around it. Also, the flight control surfaces like the elevator and the pitch of rotor blades affect to the flow around the body. Then it determines the new position and rotation of the body. This series of mechanism is performed by coupled computation between a body and flows using following equations:

$$ m\frac{{d^{2} \varvec{r}}}{{dt^{2} }} = \varvec{F}, $$
(5)
$$ I\frac{{d\varvec{\omega}}}{dt} +\varvec{\omega}\times I\varvec{\omega}= \varvec{T}, $$
(6)

where \( m \) is the mass, \( \varvec{r} \) is the position vector, \( \varvec{F} \) is the force vector, \( I \) is the inertia tensor (written in matrix form), \( \varvec{\omega} \) is the angular velocity vector and \( \varvec{T} \) is the torque vector.

3 Test Problems

To simulate a flow around a tilt-rotor plane, the multi-axis sliding mesh approach is inspected by applying it to test problems. In this section, the uniform flow and the shock tube problem are computed to verify the code.

3.1 Inspection for Geometric Conservation Law

The uniform flow passing through multi-axis sliding surfaces was computed to check whether the geometric conservation law is satisfied. The computational domain is consists of three sub-domains. The domain 1 is rotating spherical one which is embedded in the domain 2. The domain 2 is rotating cylindrical one which is embedded in the domain 3. The initial conditions of density, pressure, velocity components in the x, y and z directions are given by: \( \rho = 1.0 \), \( p = 1.0/\gamma \left( {\gamma = 1.4} \right) \), \( u = 1.0 \), \( v = 1.0 \), \( w = 1.0 \). These values are given as the boundary condition as well.

Figure 6 illustrates the history of the error of density defined by Eq. (4). The order of error is under 10−12. Moreover, we got the same result on the velocity and the pressure. Therefore, it was proven that this approach perfectly captured the uniform flow passing through multi-axis sliding surface and satisfied the geometric conservation law.

Fig. 6.
figure 6

History of error of density

Full size image
$$ Error_{i} = \hbox{max} \left( {\frac{{\left| {\rho_{i} - \rho } \right|}}{\rho }} \right). $$
(7)

3.2 Shock Tube Problem

The shock tube problem was applied to evaluate the approach compared with its exact solution. The computational domain is consists of three sub-domains. The domain 1 is spherical one which is embedded in the domain 2. The domain 2 is cylindrical one which is embedded in the domain 3 whose shape is rectangular. The domain 1 and domain 2 rotate as shown in Fig. 7. These rotating bodies have boundaries where a flow can path through and there is no shear force. Therefore the rotation of those doesn’t affect the flow. In other words, the interpolation on sliding surface being accurate, the result of the computation using the approach must be equal to that of the computation using just a rectangular domain. Thus, the validity of the approach is shown by being applied to the shock tube problem.

Fig. 7.
figure 7

Shock tube problem

Full size image

The initial conditions of density, pressure, velocity components in the x, y and z directions are given by: \( \rho_{\text{L}} = 1.0 \), \( p_{\text{L}} = 1.0/\gamma \left( {\gamma = 1.4} \right) \), \( u = 0.0 \), \( v = 0.0 \), \( w = 0.0 \) at the left of the diaphragm, and \( \rho_{\text{R}} = 0.1 \), \( p_{\text{R}} = 0.1/\gamma \) at the right of the diaphragm. The reflected condition is applied as the outer boundary condition. The number of cells is 1,005,115.

Figure 8 illustrates the result of the density distributions at t = 0.5 and t = 2.0. The result shows that the shock wave keeps the sharpness after passing through the sliding surfaces on the rotating bodies. Moreover, Fig. 9 shows the result of the density on the center line of the rectangular at t = 0.5, where that is equal to the exact solution. Thus, the validity of the approach is confirmed.

Fig. 8.
figure 8

Density contours

Full size image
Fig. 9.
figure 9

Distribution of density

Full size image

4 Application to Tilt-Rotor Plane

To achieve six degrees of freedom coupled simulation of a V-22 Osprey as a tilt-rotor plane, a combination approach with the multi-axis sliding mesh and the MCD method is used. In the simulation, hovering and yawing are performed.

4.1 Computational Mesh and Conditions

In this computation, the computational domain is divided into 9 domains (see Fig. 10). Computational meshes of each domain are shown in from Figs. 11, 12, 13, 14 and 15. These meshes are generated by using MEGG3D [16, 17]. Here, the domains 1–6 are used to perform the rotations of two blade rotors and two engine nacelles. The domains 7–9 are used to perform the vertical motion for takeoff of the plane. Total number of cells is 3,333,068. The initial conditions of density, pressure, velocity components in the x, y and z directions are given by: \( \rho = 1.0 \), \( p = 1.0/\gamma \left( {\gamma = 1.4} \right) \), \( u = 0.0 \), \( v = 0.0 \), \( w = 0.0 \). The simulation is performed under the following conditions.

Fig. 10.
figure 10

Domain decomposition around the plane

Full size image
Fig. 11.
figure 11

Mesh around rotors

Full size image
Fig. 12.
figure 12

Mesh around wings

Full size image
Fig. 13.
figure 13

Mesh around nacelles

Full size image
Fig. 14.
figure 14

Mesh around a body

Full size image
Fig. 15.
figure 15

Outer meshes

Full size image
  1. (1)

    Takeoff (The engine starts around the ground. It takes off in helicopter mode until it arrives 10.0 m high.)

  2. (2)

    Hovering and yawing (The planes of rotors tilt in the opposite direction to yaw by up to 7°. The rotational speed of rotors is constant. The collective pitch is used to keep altitude and prevent from rolling.)

4.2 Results

Figure 16 shows that an isosurface of the velocity in hovering. It found that the flow around the tilt-rotor plane is bilaterally asymmetric although the body is almost bilaterally symmetric orientation. Figure 17 shows that an isosurface of the velocity in yawing. In the figure, a history from the start of yawing to one revolution is illustrated (0, 90, 180 and 360°). The flow around the plane is completely asymmetry. For the motion of the plane, yawing is achieved by tilting the planes of rotors in the opposite direction. This occurred by the fluid force due to a coupled simulation. Moreover, the plane moved in a rough circular motion viewed from the top by not only rotating but also translating (see Fig. 18). Using the approach, we could see the complicated phenomena occurred by direct computation of the motion of rotor blade. Furthermore, the flow was simulated continuously.

Fig. 16.
figure 16

Isosurface of velocity in hovering

Full size image
Fig. 17.
figure 17

Isosurface of velocity in yawing

Full size image
Fig. 18.
figure 18

Pressure contour and trajectory of center of mass (yellow line) in yawing (Color figure online)

Full size image

5 Conclusions

To achieve six degrees of freedom coupled simulation around a tilt-rotor plane with high accuracy, the multi-axis sliding mesh approach was applied. The result of the first test problem showed that this method captured the uniform flow passing through multi-axis sliding surface and satisfied the geometric conservation law. The result of application to the shock tube problem showed that the approach can be applied to such flow. The combination of the multi-axis sliding approach and the MCD method, the flow occurred by a tilt-rotor plane was computed. Six degrees of freedom coupled simulation of hovering and yawing was simulated.