Abstract
The increasing volume of event data that is recorded by information systems during the execution of business processes creates manifold opportunities for process analytics. Specifically, conformance checking compares the behaviour as recorded by an information system to a model of desired behaviour. Unfortunately, state-of-the-art conformance checking algorithms scale exponentially in the size of both the event data and the model used as input. At the same time, event data used for analysis typically relates only to a certain interval of process execution, not the entire history. Given this inherent data incompleteness, we argue that an understanding of the overall conformance of process execution may be obtained by considering only a small fraction of a log. In this paper, we therefore present a statistical approach to ground conformance checking in trace sampling and conformance approximation. This approach reduces the runtime significantly, while still providing guarantees on the accuracy of the estimated conformance result. Comprehensive experiments with real-world and synthetic datasets illustrate that our approach speeds up state-of-the-art conformance checking algorithms by up to three orders of magnitude, while largely maintaining the analysis accuracy.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
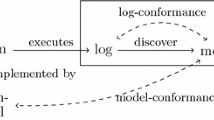
Process-oriented information systems coordinate the execution of a set of actions to reach a business goal [15]. The behaviour of such systems is commonly described by process models that define a set of activities along with execution dependencies. However, once event data is recorded during runtime, the question of conformance emerges [9]: how do the modelled behaviour of a system and its recorded behaviour relate to each other? Answering this question is required to detect, interpret, and compensate deviations between a model of a process-oriented information system and its actual execution.
Driven by trends such as process automation, data sensing, and large-scale instrumentation of process-related resources, the volume of event data and the frequency at which it is generated is increasing in today’s world: Event logs comprise up to billions of events [2]. Also, information systems are subject to frequent changes [34], so that analysis is often a continuous process, repeated when new event data becomes available.
Acknowledging the resulting need for efficient analysis, various angles have been followed to improve the runtime performance of state-of-the-art, alignment-based conformance checking algorithms [4], which suffer from an exponential worst-case complexity. Efficiency improvements have been obtained through the use of search-based methods [13, 25], planning algorithms [21], and distributed computing [16, 22]. Furthermore, several authors suggested to compromise correctness and approximate conformance results to gain efficiency, e.g., by employing approximate alignments [29] or applying divide-and-conquer schemes in the computation of conformance results [3, 12, 20, 23]. However, these approaches primarily target the applied algorithms. Fundamentally, they still require the consideration of all, possibly billions, of recorded events.
In practice, an event log is recorded for a certain interval of process execution, not the entire history. Given this inherent incompleteness of event data, which is widely acknowledged [1, 17, 26], analysis often strives for a general understanding of the conformance of process execution. This may relate, e.g., to the overall fitness of recorded and modelled behaviour [4] or the activities that denote hotspots of non-conformance [3].
In this paper, we argue that for a general understanding of the overall conformance, it is sufficient to compute conformance results for only a small fraction of an event log. Since the latter per se provides an incomplete view, minor differences in the conformance results obtained for the whole log and a partial log may be attributed to the inherent uncertainty of the conformance checking setting. We illustrate this idea with a claim handling process in Fig. 1. Here, the events recorded for the first case indicate non-conformance, as a previous claim is fetched twice (f). Considering also the second case, the average amount of non-conformance (one deviation) and the set of non-conforming activities ({F}) are the same, though, despite the different sequence of events. Considering also the third and fourth case, new information on the overall conformance of process execution is obtained. Yet, the fourth case resembles the first one. Hence, its conformance (two deviations w.r.t. the model) may be approximated based on the result of the first case (one deviation) and the difference between both event sequences (one event differs).
To realise the above ideas, we follow two complimentary angles to avoid computation of conformance results for all available data. First, we contribute an incremental approach based on trace sampling, which, for each trace, assesses whether it yields new information on the overall conformance. Assuming the view of a series of binomial experiments, we establish bounds on the error of the conformance result derived from a partial event log. Second, we show how trace sampling is combined with result approximation that, instead of computing a conformance result for a trace at hand, relies on a worst-case approximation of its implications on the overall conformance. This way, we further reduce the amount of data for which conformance results are actually computed. We instantiate this framework for two types of conformance results as mentioned above, a numerical fitness measure and a distribution of conformance issues over all activities.
In the remainder, we first give preliminaries in Sect. 2. We then introduce our approach to sample-based (Sect. 3) and approximation-based (Sect. 4) conformance checking. Experimental results using real-world and synthetic event logs are presented in Sect. 5. We review related work in Sect. 6, before we conclude in Sect. 7.
2 Preliminaries
Events and Event Logs. We adopt an event model that builds upon a set of activities \(\mathcal {A}\). An event recorded by an information system is assumed to be related to the execution of one of these activities. By \(\mathcal {E}\), we denote the universe of all events. A single execution of a process, called a trace, is modelled as a sequence of events \(\xi \in \mathcal {E}^*\), such that no event can occur in more than one trace. An event log is a set of traces, \(L \subseteq 2^{\mathcal {E}^*}\). Our example in Fig. 1b defines four traces. While each event is unique, we represent them with small letters \(\{r, p, f, u, s\}\), that indicate for which activity of the process model, denoted by respective capital letters \(\{R, P, F, U, S\}\), the execution is signalled. Two distinct traces that indicate the same sequence of activity executions are of the same trace variant.
Process Models. A process model defines the execution dependencies between the activities of a process. For our purposes, it is sufficient to abstract from specific process modelling languages and focus on the behaviour defined by a model. That is, a process model defines a set of execution sequences, \(M\subseteq \mathcal {A}^*\), that capture sequences of activity executions that lead the process to its final state. For instance, the model in Fig. 1a defines the execution sequences \(\langle R, P, F, U, S\rangle \) and \(\langle R, F, P, U, S\rangle \), potentially including additional repetitions of U. We write \(\mathcal {M}\) for the set of all process models.
Alignments. State-of-the-art techniques for conformance checking construct alignments between traces and execution sequences of a model to detect deviations [4, 23]. An alignment between a trace \(\xi \) and a model M, denoted by \(\sigma (\xi , M)\) in the remainder, is a sequence of steps, each step comprising a pair of an event and an activity, or a skip symbol \(\bot \), if an event or activity is without counterpart. For instance, for the non-conforming trace \(\xi _1\) (case 1 from Fig. 1b), an alignment is constructed as follows:

Assigning costs to skip steps, a cost-optimal alignment (not necessarily unique) is constructed for a trace in relation to all execution sequences of a model [4]. An optimal alignment then enables the quantification of non-conformance. Specifically, the fitness of a log with respect to a given model is computed as follows:
Here, \(c(\xi , M)\) is the aggregated cost of an optimal alignment \(\sigma (\xi , M)\). The denominator captures the maximum possible cost per trace, i.e., the sum of the costs of aligning a trace with an empty model, \(c(\xi , \emptyset )\), and the minimal costs of aligning an empty trace with the model, \(\min _{x \in M}c(\langle \rangle , \{x\})\). Using a standard cost function (all skip steps have equal costs), the fitness value of the example log \(\{\xi _1,\xi _2,\xi _3,\xi _4\}\) in Fig. 1b is 0.9. Alignments further enable the detection of hotspots of non-conformance. To this end, the conformance result can be defined in terms of a deviation distribution that captures the relative frequency with which an activity (not to be confused with a task of a process model) is part of a conformance violation. For a log L and a model M, this distribution follows from skip steps in the optimal alignments of all traces. It is formalised based on a bag of activities, \(dev(L, M): \mathcal {A} \rightarrow \mathbb {N}_0\) (note that multiple skip steps may relate to a single activity even in the alignment of one trace). The relative deviation frequency of an activity \(a\in \mathcal {A}\) is then obtained by dividing the number of occurrences of a in the bag of deviations by the total number of deviations, i.e., \(f_{dev(L, M)}(a)=dev(L, M)(a)/|dev(L, M)|\).
For our example in Fig. 1, assuming that skip steps relate to the highlighted trace positions, it holds that \(dev(\{\xi _1,\xi _2,\xi _3, \xi _4\},M)= [F^3,U]\) and \(f_{dev(\{\xi _1,\ldots , \xi _4\},M)}(F)=3/4\), so that the fetching of a previous claim (F) is identified as a hotspot of non-conformance.
3 Sample-Based Conformance Checking
This section describes how trace sampling can be used to improve the efficiency of conformance checking. The general idea is that it often suffices to only compute alignments for a subset of all trace variants to gain insights into the overall conformance of a log to a model. However, we randomly sample an event log trace-by-trace, not by trace variant, which avoids to load the entire log and step-wise reveals the distribution of traces among the variants. At some point, though, the sampled traces then do not provide new information on the overall conformance of the process.
In the remainder of this section, we first describe a general framework for sample-based conformance checking (Sect. 3.1), which we then instantiate for two types of conformance results: fitness (Sect. 3.2) and deviation distribution (Sect. 3.3).
3.1 Statistical Sampling Framework
To operationalise sample-based conformance checking, we regard it as a series of binomial experiments. In this, we follow a log sampling technique introduced in the context of process discovery [5, 7] and lift it to the setting of conformance checking.
Information Novelty. When parsing a log trace-by-trace, some traces may turn out to provide information on the conformance of a log to a model that is similar or equivalent to the information provided by previously encountered traces. To assess whether this is the case, we capture the conformance information associated with a log by a conformance function \(\psi : 2^{\mathcal {E}^*}\times \mathcal {M}\rightarrow \mathcal {X}\). That is, \(\psi (L, M)\) is the conformance result (of some domain \(\mathcal {X}\)) between a log L and a model M. If we are interested in the distribution of deviations, \(\psi \) provides information on the model activities for which deviations are observed, whereas for fitness, it would return the fitness value.
Based thereon, we define a random Boolean predicate \(\gamma (L', \xi , M)\) that captures whether a trace \(\xi \in \mathcal {E}^*\) provides new information on the conformance with model M, i.e., whether it changes the result obtained already for a set of previously observed traces \(L'\subseteq 2^{\mathcal {E}^*}\). Assuming that the distance between conformance results can be quantified by a function \(d: \mathcal {X} \times \mathcal {X} \rightarrow \mathbb {R}_0^+\), we define a new information predicate as:
Here, \(\epsilon \in \mathbb {R}^{+}_0\) is a relaxation parameter. If incorporating trace \(\xi \) changes the conformance result by more than \(\epsilon \), then it adds new information over \(L'\).
Framework. We exploit the notion of information novelty for hypothesis testing when sampling traces from an event log L. We determine when enough sampled traces have been included in a log \(L' \subseteq L\) to derive an understanding of its overall conformance to a model M. Following the interpretation of log sampling as a series of binomial experiments [5], \(L'\) is regarded as sufficient if the algorithm consecutively draws a certain number of traces that did not contain new information. Specifically, with \(\delta \) as a measure that bounds the probability of a newly sampled trace to provide new information over \(L'\), at a significance level \(\alpha \), a minimum sample size N is computed. Based on the normal approximation to the binomial distribution, the latter is given as \(N\ge {1}/{2 \delta } \left( -2\delta ^2 + z^2 + \sqrt{z}\right) \), where z corresponds to the realisation of a standardised normal random variable for \(1-\alpha \) (one-sided hypothesis test). As such, N is calculated given values for \(\delta \) and \(\alpha \) for the desired levels of similarity and significance, respectively.
Consider \(\alpha =0.01\) and \(\delta =0.05\), so that \(N \ge 128\). Hence, after observing 128 traces without new information, sampling can be stopped knowing with 0.99 confidence that the probability of finding new information in the remaining log is less than 0.05.
Using the above formulation, our framework for sample-based conformance checking is presented in Algorithm 1. The algorithm takes as input an event log L, a process model M, the number of trials that need to fail N, a predicate \(\gamma \) to determine whether a trace provides new information, and a conformance function \(\psi \). Going through L trace-by-trace (lines 3–12), the algorithm conducts a series of binomial experiments that check, if a newly sampled trace provides new information according to the predicate \(\gamma \) (line 5 ). Once N consecutive traces without new information have been selected, the procedure stops and the conformance result is derived based on the sampled log \(L'\).
Result Re-use. Note that the algorithm provides a conceptual view, in the sense that checking the new information predicate \(\gamma (L',\xi ,M)\) in line 5 according to Eq. 2, requires the computation of \(\psi (L', M)\) and \(\psi (\{\xi \}\cup L', M)\) in each iteration. A technical realisation of this algorithm, of course, shall exploit that most types of conformance results can be computed incrementally. For instance, considering fitness and the deviation distribution, an alignment is computed only once per trace variant, i.e., per unique sequence of activity executions, and reused in the iterations of the algorithm. Also, the value of \(\psi (L', M)\) for \(\gamma (L',\xi ,M)\) in line 5 is always known from the previous iteration, while the conformance result in line 13 is not actually computed at this stage, as the respective result is known from the last evaluation of \(\gamma (L',\xi ,M)\).
In the next sections, we discuss how to define \(\gamma \) when the conformance function assesses the fitness of a log to a model, or the observed deviation distribution.
3.2 Sample-Based Fitness
The overall conformance of a log to a model may be assessed by considering the log fitness (see Sect. 2) as a conformance function, \(\psi _{ fit }(L,M) = \text {fitness}(L, M)\). Then, determining whether a trace \(\xi \) provides new information over a log sample \(L'\) requires us to assess, if incorporating \(\xi \) leads to a difference in the overall fitness for the sampled log. Following Eq. 2, we capture this by computing the absolute difference between the fitness value for traces in the sample \(L'\) and the value of the sample plus the new trace:
If this distance is smaller than the relaxation parameter \(\epsilon \), the change in the overall fitness value induced by trace \(\xi \) is considered to be negligible.

To illustrate this, consider a scenario with \(\epsilon = 0.03\) and a sample consisting of the traces \(\xi _1\) and \(\xi _3\) of our running example (Fig. 1). Then, the log fitness for \(\{\xi _1,\xi _3\}\) is 0.95. In this situation, if the next sampled trace is \(\xi _2\), the distance function yields \(\left| \text {fitness}(\{\xi _1,\xi _3\}, M) - \text {fitness}(\{\xi _1,\xi _2,\xi _3\}, M) \right| = 0.95 - 0.93 = 0.02\). In this case, since the distance is smaller than \(\epsilon \), we would conclude that the additional consideration of \(\xi _2\) does not provide new information. By contrast, considering trace \(\xi _4\) would yield a distance of \(0.95 - 0.89 = 0.06\). This indicates that trace \(\xi _4\) would imply a considerable change in the overall fitness value, i.e., it provides new information.
3.3 Sample-Based Deviation Distributions
Next, we instantiate the above framework for conformance checking based on the deviation distribution. As detailed in Sect. 2, this distribution captures the relative frequency with which activities are related to conformance issues.
To decide whether a trace \(\xi \) provides new information over a log sample \(L'\), we assess if the deviations obtained for \(\xi \) lead to a considerable difference in the overall deviation distribution. As such, the distance function for the predicate \(\gamma \) needs to quantify the difference between two discrete frequency distributions. This suggests to employ the L1-distance, also known as the Manhattan distance, as a measure:
Taking up our example from Fig. 1, processing only the trace \(\xi _1\), all deviations are related to the activity of fetching an earlier claim, i.e., \(f_{dev(\{\xi _1\},M)}(F)=1\). Notably, this does not change when incorporating traces \(\xi _2\) and \(\xi _3\), i.e., \(f_{dev(\{\xi _1, \xi _2, \xi _3\},M)}(F)=1\), as they do not provide new information in terms of the deviation distribution. If, after processing trace \(\xi _1\), however, we sample \(\xi _4\), we do observe such a difference: based on \(f_{dev(\{\xi _1,\xi _4\},M)}(F)=2/3\) and \(f_{dev(\{\xi _1,\xi _4\},M)}(U)=1/3\), we compute a Manhattan distance of 2/3. With a relaxation parameter \(\epsilon \) that is smaller than this value, we conclude that \(\xi _4\) provides novel information.
Given the distance functions based on trace fitness and deviation distribution, it is interesting to note that these behave differently, as illustrated in our example: If the log is \(\{\xi _1, \xi _2\}\) and trace \(\xi _3\) is sampled next, the overall fitness changes. Yet, since \(\xi _3\) is a conforming trace, it does not provide new information on the distribution of deviations.
4 Approximation-Based Conformance Checking
This section shows how conformance results can be approximated, further avoiding the need to compute a conformance result for certain traces. Our idea is to derive a worst-case approximation for traces that are similar to variants for which results have previously been derived. Approximation complements the sampling method of Sect. 3: Even when a trace of a yet unseen variant is sampled, we decide whether to compute an actual conformance result or whether to approximate it. As such, the decision on whether a trace provides new information may be taken either based on a computed or an approximated result.
Against this background, our technique for approximation-based conformance checking, formalised in Algorithm 2, extends our procedure given in Algorithm 1. In fact, it primarily provides a realisation of checking the new information predicate \(\gamma (L',\xi ,M )\), as done in line 5 of Algorithm 1. That is, whether the sampled trace \(\xi \), of an unseen variant, provides new information is potentially decided based on the approximated, rather than computed impact of it on the overall conformance result. At the same time, however, the algorithm also needs to keep track of all sampled traces \(L''\subseteq L'\), for which the approximated results shall be used whenever a conformance result is computed. This leads to an adaptation of the conformance function \(\psi \), i.e., we consider a partially approximating conformance function \(\hat{\psi }: 2^{\mathcal {E}^*}\times 2^{\mathcal {E}^*}\times \mathcal {M}\rightarrow \mathcal {X}\). Given a log \(L'\) and a subset \(L''\subseteq L'\), this function approximates the conformance result \(\psi (L', M)\) by computing solely \(\psi (L'\setminus L'', M)\), i.e., the impact of traces \(L''\) is not precisely computed. In the same way, to use the approximation technique as part of sample-based conformance checking, the use of the conformance function \(\psi \) in Algorithm 1 also has to be adapted accordingly.
Turning to the details of Algorithm 2, its input includes a log sample \(L'\), a sampled trace \(\xi \notin L'\), and a process model M, i.e., the arguments of \(\gamma \) in line 5 of Algorithm 1, as well as a distance function d and relaxation parameter \(\epsilon \) from the definition of \(\gamma \) (Eq. 2). Moreover, there is a similarity threshold k to determine which traces may be used for approximation. Finally, the aforementioned set of traces \(L''\) for which results shall be approximated and the respective adapted conformance function \(\hat{\psi }\) are given as input.
From the sampled traces for which approximation is not applied (i.e., \(L'\setminus L''\)), the algorithm first selects the trace that is most similar to \(\xi \), referred to as the reference trace \(\xi _r\) (line 1). Then, we assess whether this similarity is above the threshold k (line 2). If not, we check the trace for new information as done before, just using the adapted conformance function (lines 9–10). If \(\xi _r\) is sufficiently similar, however, we perform a worst-case approximation of the impact of \(\xi \) on the overall conformance result based on \(\xi _{r}\) (line 3). As part of that, we may obtain several different approximations \(\varPhi \), each of which is checked whether it indicates new information over the current sample \(L'\) (line 4). Only if this is not the case, we conclude that \(\xi \) indeed does not provide new information and, by adding it to \(L''\) make sure that its impact on the overall conformance will always only be approximated, but never precisely computed (line 7).

Next, we give details on the assessment of trace similarity (function sim, Sect. 4.1) and the conformance result approximation (function approx, Sect. 4.2).
4.1 Trace Similarity
Given a trace \(\xi \) and the part of the sample log for which approximation did not apply (\(L'\setminus L''\)), Algorithm 2 requires us to identify a reference trace \(\xi _r\) that is most similar according to some function \(sim:\mathcal {E}^*\times \mathcal {E}^*\rightarrow [0,1]\). As we consider conformance results that are based on alignments, we define this similarity function based on the alignment cost of two traces. To this end, we consider a function \(c_t\), which, in the spirit of function c discussed in Sect. 2, is the sum of the costs assigned to skip steps in an optimal alignment of two traces. To obtain a similarity measure, we normalise this aggregated cost by a maximal cost, which is obtained by aligning each trace with an empty trace. This normalisation resembles the one discussed for the fitness measure in Sect. 2. We define the similarity function for traces as \(sim(\xi , \xi ') = 1 - c_t(\xi , \xi ')/(c_t(\xi , \langle \rangle )+ c_t(\xi ', \langle \rangle ))\).
Considering trace \(\xi _4 = \langle r, p, f, f, s \rangle \) of our running example, the most similar trace (assuming equal costs for all skip steps) is \(\xi _1 = \langle r, p, f, f, u, s \rangle \), with \(c_t(\xi _1, \xi _4) = 1\) and, thus, \(sim(\xi _1, \xi _4) = 10/11\).
4.2 Conformance Result Approximation
In the approximation step of Algorithm 2, we derive a set of worst-case approximations of the impact of the trace \(\xi \) on the overall conformance result, using the reference trace \(\xi _{r}\) (which is at least k-similar). Based thereon, it is decided whether \(\xi \) provides new information. The approximation, however, depends on the type of conformance result.
Fitness Approximation. To approximate the impact of trace \(\xi \) on the overall fitness, we compute a single value, i.e., \(approx(\xi ,\xi _r, L', M)\) in line 3 of Algorithm 2 yields a singleton set. This value is derived by reformulating Eq. 3, which captures the change in fitness induced by a sample trace. That is, we assess the difference between the current fitness, \(\text {fitness}(L', M)\), and an approximation of the fitness when incorporating \(\xi \), i.e., \(\text {fitness}(\{\xi \} \cup L', M)\). This approximation, denoted by \(\widehat{ fit }(\xi ,\xi _r, L', M)\), is derived from (i) the change in fitness induced by the reference trace \(\xi _r\), and (ii) the differences between \(\xi \) and \(\xi _r\). The former is assessed using the aggregated alignment cost \(c(\xi _r, M)\), whereas the latter leverages the aggregated cost of aligning the traces, \(c_t(\xi , \xi _r)\). Normalising these costs, function \(approx_{ fit }(\xi ,\xi _r, L', M)\) yields a worst-case approximation for the change in overall fitness imposed by \(\xi \), as follows:
Turning to our running example, assume that we have sampled \(\{\xi _1,\xi _2\}\) and computed the precise fitness value based on both traces, which is \(1 - 2 / (12 + 10) \approx 0.909\) using a standard cost function. If trace \(\xi _4\) is sampled next, we approximate its impact using the similar trace \(\xi _1\). To this end, we consider \(c(\xi _1,M) = 1\) and \(c_t(\xi _1, \xi _4) = 1\), which yields an approximated fitness value of \(1 - (2 + 1 + 1)/(12 + 6 + 15) = 1 - 4/33\approx 0.879\). This is close to the actual fitness value for \(\{\xi _1,\xi _2, \xi _4\}\), which is \(1 - 4/(17 + 15)\approx 0.875\). The minor difference stems from \(\xi _1\) being slightly longer than \(\xi _4\).
Deviation Distribution Approximation. To approximate the impact of trace \(\xi \) on the deviation distribution, we follow a similar approach as for fitness approximation. However, we note that the approximation function here yields a set of possible values, as there are multiple different distributions to be considered when measuring the Manhattan distance to the current distribution. The reason being that the difference between \(\xi \) and the reference trace \(\xi _r\) induces a set of possible changes of the distribution.
Specifically, we denote by \(ed(\xi ,\xi _r)\) the edit distance of the two traces, i.e., the pure number of skip steps in their alignment. This number gives an upper bound for the number of conformance issues that need to be incorporated in addition to those stemming from the alignment of the reference trace and the model, i.e., \(dev(\{\xi _r\}, M)\). Yet, the exact activities are not known, so that we need to consider all bags of activities of size \(ed(\xi ,\xi _r)\), the set of which is denoted by \([\mathcal {A}]^{ed(\xi ,\xi _r)}\). Each of these bags leads to a different approximation \(\widehat{f_{dev}}(\beta , \xi _r, L', M)\) of the distribution \(f_{dev(\{\xi \}\cup L', M)}\) that we are actually interested in. We compute those as follows:
Consider our example again: Based on \(\{\xi _1,\xi _2\}\), we determine that \(dev(\big \{\xi _1,\xi _2\big \},M)= [F^2]\) and \(f_{dev(\{\xi _1,\xi _2\},M)}(F)=1\). If \(\xi _4\) is then sampled, we obtain an approximation based on \(dev(\{\xi _1\},M)= [F]\) and \(ed(\xi _4,\xi _1)=1\). We therefore consider the change in the distribution incurred by approximating the deviations of \(\xi _4\) as \([F]\uplus \beta \) with \(\beta \in \{[R], [P], [F],[U], [S]\}\). For instance, \(\widehat{f_{dev}}([R], \xi _4, \{\xi _1,\xi _2\}, M)\) yields a distribution assigning relative frequencies of 3/4 and 1/4 to activities F and R, respectively.
The above approximation may be tuned heuristically by narrowing the set of activities that are considered for \(\beta \), i.e., the possible deviations incurred by the difference between \(\xi \) and \(\xi _r\). While this means that \(\widehat{f_{dev}}\) is no longer a worst-case approximation, it may steer the approximation in practice, hinting at which activities shall be considered for possible deviations. Such an approach is also beneficial for performance reasons: Since \(\beta \) may be any bag built of the respective activities, the exponential blow-up limits the applicability of the approximation to traces that are rather similar, i.e., for which \(ed(\xi ,\xi _r)\) is small.
Here, we describe one specific heuristic. First, we determine the overlap between \(\xi \) and \(\xi _r\) in terms of their maximal shared prefix and suffix of activities, for which the execution is signalled by their events. Next, we determine the events that are not part of the shared prefix and suffix, and derive the activities referenced by these events. Only these activities are then considered for the construction of \(\beta \).
In our example, traces \(\xi _1\) and \(\xi _4\) share the prefix \(\langle r, p, f, f\rangle \) and suffix \(\langle s \rangle \). Thus, \(\xi _1\) contains one event between the shared prefix and suffix, u, while there is none for \(\xi _4\). Hence, we consider a single bag of deviations, \(\beta =[U]\), and \(\widehat{f_{dev}}([U], \xi _4, \{\xi _1,\xi _2\}, M)\) is the only distribution considered in the approximation.
5 Evaluation
This section reports on an experimental evaluation of the proposed techniques for sample-based and approximation-based conformance checking. Section 5.1 describes the three real-world and seven synthetic event logs used in the experimental setup, described in Sect. 5.2. The evaluation results demonstrate that our techniques achieve considerable efficiency gains, while still providing highly accurate conformance results (Sect. 5.3).
5.1 Datasets
We conducted our experiments based on three real-world and seven synthetic event logs, which are all publicly available.
Real-World Data. The three real-world event logs differ considerably in terms of the number of unique traces they contain, as well as their average trace lengths, which represent key characteristics for our approach.
-
BPI-12 [31] is a log of a process for loan or overdraft applications at a Dutch financial institute that was part of the Business Process Intelligence (BPI) Challenge. The log contains 13,087 traces (4,366 variants), with 20.0 events per case (avg.).
-
BPI-14 [32] is the log of an ICT incident management process used in the BPI Challenge. For the experiments, we employed the event log of incidence activities, containing 46,616 traces (31,725 variants), with 7.3 events per case (avg.).
-
Traffic Fines [11] is a log of an information system managing road traffic fines. The log contains 150,370 traces (231 variants), with 3.7 events per case (avg.).
We obtained accompanying process models for these logs using the inductive miner infrequent [19] with its default parameter settings (i.e., 20% noise filtering).
Synthetic Data. To analyse the scalability of our techniques, we considered a synthetic dataset designed to stress-test conformance checking techniques [24]. It consists of seven process models and accompanying event logs. The models are considerably large and complex, as characterised in Table 1, which impacts the computation of alignments. Furthermore, the included event logs consist of a high number of variants (compared to the number of traces), which may affect the effectiveness of log sampling.
5.2 Experimental Setup
We employed the following measures and experimental setup to conduct the evaluation.
Measures. We measure the efficiency of our techniques by the fraction of traces from a log required to obtain our conformance results. This fraction indicates for how many traces the conformance computation was not needed due to the trace not being sampled, or the result being approximated. Simultaneously, we consider the fraction of the total trace variants for which our techniques actually had to establish alignments. As these fractions provide us with analytical measures of efficiency, we also assess the runtime of our techniques, based on a prototypical implementation. Again, this is compared to the runtime of the conformance checking over the complete log. Finally, we assess the impact of sampling and approximation on the accuracy of conformance results. We determine the accuracy by comparing the results, i.e., the fitness value or the deviation distribution, obtained using sampling and approximation, to the results for the total log.
All presented results are determined based on 20 experimental runs (i.e., replications) of which we report on the mean value, along with the 10th and 90th percentiles.
Environment. Our approach has been implemented as a plugin in ProM [33], which is publicly available.Footnote 1 For the computation of alignments, we rely on the ProM implementation of the search-based technique recently proposed in [13]. Runtime measurements have been obtained on a PC (Dual-Core, 2.5 GHz, 8 GB RAM) running Oracle Java 1.8.
5.3 Evaluation Results
This section first considers the overall efficiency and accuracy of our approach on the real-world event logs, using default parameter values (\(\delta = 0.01\), \(\alpha = 0.99\), \(\epsilon = 0.01\), and \(k = 1/3\)), before conducting a sensitivity analysis in which these values are varied. Lastly, we demonstrate the scalability of our approaches by showing that their performance also applies to complex, synthetic datasets.
Efficiency. We first explore the efficiency of our approach in terms of sample size and runtime for four configurations: conformance in terms of fitness, without (f) and with approximation (fa), as well as for the deviation distribution without (d) and with approximation (da). Figure 2 reveals that all configurations only need to consider a tiny fraction of the complete log. For instance, for BPI-14, the sample-based fitness computation (f) requires only 685 traces (on average) out of the total of 46,616 traces (i.e., 1.5% of the log). This sample included traces from 144 out of the total 31,725 variants (less than 0.5%), which means that the approach established just 144 alignments. As expected, these gains are propagated to the runtime of our approach, as shown in Fig. 3.
When looking at the overall efficiency results, we observe that the additional use of approximation generally does not lead to considerable improvements in comparison to just sampling. However, this is notably different for the deviation distribution of the Traffic Fines dataset. Here, without approximation, the sample size is 1323 on average (0.88%), whereas the sample size drops to 713 traces (0.47%) with approximation (da). Hence, approximation appears to be more important if sampling alone is not as effective.
Accuracy. The drastic gains in efficiency are obtained while maintaining highly accurate conformance results. According to Fig. 4, the fitness computed using sample-based conformance checking differs by less than 0.1% from the original fitness (indicated by the dashed line). Since the accuracy in terms of deviation distribution is harder to capture in a single value, we use Fig. 5 to demonstrate that the deviation distribution obtained by our sample-based technique closely follows the distribution for the complete log. In decreasing order, Fig. 5 depicts the activities with their numbers of deviations observed in the complete log and in the sampled log. As shown, our technique clearly identifies which activities are most often affected by deviations, i.e., our technique correctly identifies the main hotspots of non-conformance. Although, for clarity, not depicted, our approach including approximation achieved comparable results.
Parameter Sensitivity. We performed a parameter sensitivity analysis using sample-based conformance checking on the BPI-12 dataset. We explored how parameters \(\delta \) (probability bound), \(\alpha \) (significance value), and \(\epsilon \) (relaxedness value), affect the performance of our approach in terms of efficiency (number of traces) and accuracy (fitness).Footnote 2 Figure 6 shows that selection of \(\delta \) and \(\alpha \) have a considerable impact on the sample required for conformance checking. For instance, for \(\delta = 0.01\) we require an average sample size of 684.9, whereas when we relax the bound to \(\delta = 0.10\), the average size is reduced to 85.8 traces. For \(\alpha \), i.e., the confidence, we observe a range from 296.5 to 684.9 traces. By contrast, varying epsilon is shown to result in only marginal differences (ranging between 659.0 and 684.9). Still, for all these results, it should be considered that even the largest sample sizes represent only 5% of the traces in the original log.
Notably, as shown in Fig. 7, the average accuracy of our approach remains highly stable throughout this sensitivity analysis, ranging from 0.711 to 0.726. However, we do observe that the variance across replications differs for the parameter settings using smaller sample sizes, specifically for \(\delta = 0.1\). Here, the obtained fitness values range between 0.67 and 0.76. This indicates that for such sample sizes, the selection of the particular sample may impact the obtained conformance result in some replications.
Scalability. The results obtained for the synthetic datasets confirm that our approaches are able to provide highly accurate conformance checking results in a small fraction of the runtime. Here, we reflect on experiments performed using our fitness-based sampling approach with \(\delta = 0.05\), \(\alpha = 0.99\), and \(\epsilon = 0.01\). Figure 8 shows that, for six out of seven cases, runtime is reduced to 21.2% to 25.5% of the time needed for the total log (sample sizes range from 10.7% to 12.2%). At the same time, for all cases, the obtained fitness results are virtually equivalent to those of the total log, see Fig. 9, where the fitness values of the total logs are given by the crosses. When comparing these results to those of the real-world datasets, it should be noted that the synthetic logs hardly have any re-occurring trace variants, which makes it harder to generalize over the sampled results. This is particularly pronounced for process PrC: There is virtually no difference between the fitness obtained for the total log and the samples. Yet, the relatively low fitness value of 0.57 along with a comparatively small number of traces in the log (500 vs. 1,200) lead to a runtime of 59% with sampling. Still, overall, the results on the synthetic data demonstrate that our approach is beneficial in highly complex scenarios.
6 Related Work
Conformance checking can be grounded in various notions. Non-conformance may be detected based on a comparison of sets of binary relations defined over events of a log and activities of a model, respectively [35]. Other work suggests to ‘replay’ traces in a process model, thereby identifying whether events denote valid activity executions [27]. However, both of these streams have limitations with respect to completeness [9]. Therefore, alignment-based conformance checking techniques [4, 23], on which we focus in this work, are widely recognized as the state-of-the-art.
Acknowledging the complexity associated with the establishment of alignments, various approaches [13, 16, 25, 28], discussed in Sect. 1, have been developed to improve runtime efficiency. Other work also aims to achieve efficiency gains by approximating alignments, cf., [14, 30]. While these approaches can lead to efficiency gains, all of them fundamentally depend on the consideration of an entire event log. Moreover, our angle for approximation is different: We do not approximate alignments, but estimate a conformance result (fitness, deviation distribution) based on the distance between traces.
The sampling technique that we employ to avoid this is based on sampling used in sequence databases, i.e., datasets that contain traces. Sampling techniques for event logs have been previously applied for specification mining [10], for mining of Markov Chains [6], and for process discovery [5, 8]. However, we are the first to apply these sampling techniques to conformance checking, a use case in which computational efficiency is arguably even more important than in discovery scenarios.
7 Conclusion
In this paper, we argued that insights into the overall conformance of an event log with respect to a process model can be obtained without computing conformance results for all traces. Specifically, we presented two angles to achieve efficient conformance checking: First, through trace sampling, we achieve that only a small share of the traces of a log are considered in the first place. By phrasing this sampling as a series of random experiments, we are able to give guarantees on the introduced error in terms of a potential difference of the overall conformance result. Second, we introduced result approximation as a means to avoid the computation of conformance results even for some of the sampled traces. Exploiting similarities of two traces, we derive an upper bound for the conformance of one trace based on the conformance of another trace. Both techniques, trace sampling and result approximation, have been instantiated for two notions of conformance results, fitness as a numerical measure of overall conformance and the deviation distribution that highlights hotspots of non-conformance in terms of individual activities.
Our experiments highlight dramatic improvements in terms of conformance checking efficiency: Only 0.1% to 1% of the traces of real-world event logs (12% for synthetic data) need to be considered, which leads to corresponding speed-ups of the observed runtimes. At the same time, the obtained conformance results, whether defined as fitness or the deviation distribution, are virtually equivalent to those obtained for the total log.
In future work, we intend to lift our ideas to conformance checking that incorporates branching conditions in a process model or temporal deadlines. Moreover, we strive for an integration of divide-and-conquer schemes [18] in our approximation approach.
Notes
- 1.
- 2.
While keeping the other parameter values stable at their respective defaults.
References
Van der Aalst, W.M.P.: Process Mining - Discovery, Conformance and Enhancement of Business Processes. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19345-3
Aalst, W.M.P.: Data scientist: the engineer of the future. In: Mertins, K., Bénaben, F., Poler, R., Bourrières, J.-P. (eds.) Enterprise Interoperability VI. PIC, vol. 7, pp. 13–26. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-04948-9_2
der Aalst, W.M.P.V., Verbeek, H.M.W.: Process discovery and conformance checking using passages. Fundam. Inform. 131(1), 103–138 (2014)
Adriansyah, A., van Dongen, B., Van der Aalst, W.M.P.: Conformance checking using cost-based fitness analysis. In: EDOC, pp. 55–64 (2011)
Bauer, M., Senderovich, A., Gal, A., Grunske, L., Weidlich, M.: How much event data is enough? A statistical framework for process discovery. In: CAiSE, pp. 239–256 (2018)
Biermann, A.W., Feldman, J.A.: On the synthesis of finite-state machines from samples of their behavior. IEEE Trans. Comput. 100(6), 592–597 (1972)
Busany, N., Maoz, S.: Behavioral log analysis with statistical guarantees. In: ICSE, pp. 877–887. ACM (2016)
Carmona, J., Cortadella, J.: Process mining meets abstract interpretation. In: Balcázar, J.L., Bonchi, F., Gionis, A., Sebag, M. (eds.) ECML PKDD 2010. LNCS (LNAI), vol. 6321, pp. 184–199. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-15880-3_18
Carmona, J., van Dongen, B., Solti, A., Weidlich, M.: Conformance Checking - Relating Processes and Models. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-99414-7
Cohen, H., Maoz, S.: Have we seen enough traces? In: ASE, pp. 93–103. IEEE (2015)
De Leoni, M.M., Mannhardt, F.F.: Road traffic fine management process (2015). https://doi.org/10.4121/uuid:270fd440-1057-4fb9-89a9-b699b47990f5
Dixit, P.M., Buijs, J.C.A.M., Verbeek, H.M.W., van der Aalst, W.M.P.: Fast incremental conformance analysis for interactive process discovery. In: Abramowicz, W., Paschke, A. (eds.) BIS 2018. LNBIP, vol. 320, pp. 163–175. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-93931-5_12
Dongen, B.F.: Efficiently computing alignments - using the extended marking equation. In: Weske, M., Montali, M., Weber, I., vom Brocke, J. (eds.) BPM 2018. LNCS, vol. 11080, pp. 197–214. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98648-7_12
van Dongen, B., Carmona, J., Chatain, T., Taymouri, F.: Aligning modeled and observed behavior: a compromise between computation complexity and quality. In: Dubois, E., Pohl, K. (eds.) CAiSE 2017. LNCS, vol. 10253, pp. 94–109. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-59536-8_7
Dumas, M., Rosa, M.L., Mendling, J., Reijers, H.A.: Fundamentals of Business Process Management, 2nd edn. Springer, Heidelberg (2018). https://doi.org/10.1007/978-3-662-56509-4
Evermann, J.: Scalable process discovery using map-reduce. IEEE TSC 9(3), 469–481 (2016)
van Hee, K.M., Liu, Z., Sidorova, N.: Is my event log complete? - a probabilistic approach to process mining. In: International Conference on Research Challenges in Information Science, pp. 1–7 (2011)
Lee, W.L.J., Verbeek, H.M.W., Munoz-Gama, J., der Aalst, W.M.P.V., Sepúlveda, M.: Recomposing conformance: closing the circle on decomposed alignment-based conformance checking in process mining. Inf. Sci. 466, 55–91 (2018)
Leemans, S.J.J., Fahland, D., van der Aalst, W.M.P.: Discovering block-structured process models from event logs containing infrequent behaviour. In: Lohmann, N., Song, M., Wohed, P. (eds.) BPM 2013. LNBIP, vol. 171, pp. 66–78. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-06257-0_6
Leemans, S.J.J., Fahland, D., der Aalst, W.M.P.V.: Scalable process discovery and conformance checking. Softw. Syst. Model. 2, 599–631 (2018)
de Leoni, M., Marrella, A.: How planning techniques can help process mining: the conformance-checking case. In: Italian Symposium on Advanced Database Systems, p. 283 (2017)
Luo, C., He, F., Ghezzi, C.: Inferring software behavioral models with MapReduce. Sci. Comput. Program. 145, 13–36 (2017)
Munoz-Gama, J., Carmona, J., van der Aalst, W.: Single-entry single-exit decomposed conformance checking. Inf. Syst. 46, 102–122 (2014)
(Jorge) Munoz-Gama, J.: Conformance checking in the large (dataset) (2013). https://data.4tu.nl/repository/uuid:44c32783-15d0-4dbd-af8a-78b97be3de49
Reißner, D., Conforti, R., Dumas, M., Rosa, M.L., Armas-Cervantes, A.: Scalable conformance checking of business processes. In: Panetto, H., et al. (eds.) OTM 2017. LNCS, vol. 10573, pp. 607–627. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-69462-7_38
Rogge-Solti, A., Senderovich, A., Weidlich, M., Mendling, J., Gal, A.: In log and model we trust? A generalized conformance checking framework. In: La Rosa, M., Loos, P., Pastor, O. (eds.) BPM 2016. LNCS, vol. 9850, pp. 179–196. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45348-4_11
Rozinat, A., Van der Aalst, W.M.P.: Conformance checking of processes based on monitoring real behavior. Inf. Syst. 33(1), 64–95 (2008)
Taymouri, F., Carmona, J.: Model and event log reductions to boost the computation of alignments. In: Ceravolo, P., Guetl, C., Rinderle-Ma, S. (eds.) SIMPDA 2016. LNBIP, vol. 307, pp. 1–21. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-74161-1_1
Taymouri, F., Carmona, J.: A recursive paradigm for aligning observed behavior of large structured process models. In: La Rosa, M., Loos, P., Pastor, O. (eds.) BPM 2016. LNCS, vol. 9850, pp. 197–214. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45348-4_12
Taymouri, F., Carmona, J.: An evolutionary technique to approximate multiple optimal alignments. In: Weske, M., Montali, M., Weber, I., vom Brocke, J. (eds.) BPM 2018. LNCS, vol. 11080, pp. 215–232. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-98648-7_13
Van Dongen, B.: BPI Challenge 2012 (2012). https://doi.org/10.4121/uuid:3926db30-f712-4394-aebc-75976070e91f
Van Dongen, B.: BPI Challenge 2014 (2014). https://doi.org/10.4121/uuid:c3e5d162-0cfd-4bb0-bd82-af5268819c35
Verbeek, E., Buijs, J.C.A.M., van Dongen, B.F., der Aalst, W.M.P.V.: ProM 6: the process mining toolkit. In: Business Process Management (Demonstration Track) (2010)
Weber, B., Reichert, M., Rinderle-Ma, S.: Change patterns and change support features - enhancing flexibility in process-aware information systems. DKE 66(3), 438–466 (2008)
Weidlich, M., Polyvyanyy, A., Desai, N., Mendling, J., Weske, M.: Process compliance analysis based on behavioural profiles. Inf. Syst. 36(7), 1009–1025 (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Bauer, M., van der Aa, H., Weidlich, M. (2019). Estimating Process Conformance by Trace Sampling and Result Approximation. In: Hildebrandt, T., van Dongen, B., Röglinger, M., Mendling, J. (eds) Business Process Management. BPM 2019. Lecture Notes in Computer Science(), vol 11675. Springer, Cham. https://doi.org/10.1007/978-3-030-26619-6_13
Download citation
DOI: https://doi.org/10.1007/978-3-030-26619-6_13
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26618-9
Online ISBN: 978-3-030-26619-6
eBook Packages: Computer ScienceComputer Science (R0)