Abstract
In this paper, we propose a new leakage-resilient identity-based encryption (IBE) scheme that is secure against chosen-ciphertext attacks (CCA) in the bounded memory leakage model. It is the first CCA-secure leakage-resilient IBE scheme which does not depend on \(\mathtt {q}\)-type assumptions. More precisely, it is secure under the DLIN assumption for symmetric bilinear groups and under the XDLIN assumption for asymmetric bilinear groups, respectively.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
Abe, M., Chase, M., David, B., Kohlweiss, M., Nishimaki, R., Ohkubo, M.: Constant-size structure-preserving signatures: generic constructions and simple assumptions. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 4–24. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-34961-4_3
Akavia, A., Goldwasser, S., Vaikuntanathan, V.: Simultaneous hardcore bits and cryptography against memory attacks. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 474–495. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-00457-5_28
Alwen, J., Dodis, Y., Naor, M., Segev, G., Walfish, S., Wichs, D.: Public-key encryption in the bounded-retrieval model. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 113–134. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-13190-5_6
Alwen, J., Dodis, Y., Wichs, D.: Leakage-resilient public-key cryptography in the bounded-retrieval model. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 36–54. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_3
Brakerski, Z., Kalai, Y.T., Katz, J., Vaikuntanathan, V.: Overcoming the hole in the bucket: public-key cryptography resilient to continual memory leakage. In: FOCS, pp. 501–510 (2010)
Brier, E., Clavier, C., Olivier, F.: Correlation power analysis with a leakage model. In: Joye, M., Quisquater, J.-J. (eds.) CHES 2004. LNCS, vol. 3156, pp. 16–29. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28632-5_2
Cheon, J.H.: Security analysis of the strong Diffie-Hellman problem. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 1–11. Springer, Heidelberg (2006). https://doi.org/10.1007/11761679_1
Chow, S.S., Dodis, Y., Rouselakis, Y., Waters, B.: Practical leakage-resilient identity-based encryption from simple assumptions. In: ACM CCS, pp. 152–161 (2010)
Dodis, Y., Haralambiev, K., López-Alt, A., Wichs, D.: Cryptography against continuous memory attacks. In: FOCS, pp. 511–520 (2010)
Dodis, Y., Kalai, Y.T., Lovett, S.: On cryptography with auxiliary input. In: STOC, pp. 621–630 (2009)
Dodis, Y., Ostrovsky, R., Reyzin, L., Smith, A.: Fuzzy extractors: how to generate strong keys from biometrics and other noisy data. SIAM J. Comput. 38(1), 97–139 (2008)
Escala, A., Herold, G., Kiltz, E., Ràfols, C., Villar, J.: An algebraic framework for Diffie-Hellman assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 129–147. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40084-1_8
Galbraith, S.D., Paterson, K.G., Smart, N.P.: Pairings for cryptographers. Discret. Appl. Math. 156(16), 3113–3121 (2008)
Gandolfi, K., Mourtel, C., Olivier, F.: Electromagnetic analysis: concrete results. In: Koç, Ç.K., Naccache, D., Paar, C. (eds.) CHES 2001. LNCS, vol. 2162, pp. 251–261. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-44709-1_21
Halderman, J.A., et al.: Lest we remember: cold boot attacks on encryption keys. In: USENIX, pp. 45–60 (2008)
Halevi, S., Lin, H.: After-the-fact leakage in public-key encryption. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 107–124. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_8
Hofheinz, D., Kiltz, E.: Programmable hash functions and their applications. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 21–38. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-85174-5_2
Katz, J., Vaikuntanathan, V.: Signature schemes with bounded leakage resilience. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 703–720. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-10366-7_41
Kiltz, E., Galindo, D.: Direct chosen-ciphertext secure identity-based key encapsulation without random oracles. Theor. Comput. Sci. 410(47–49), 5093–5111 (2009)
Kocher, P., Jaffe, J., Jun, B.: Differential power analysis. In: Wiener, M. (ed.) CRYPTO 1999. LNCS, vol. 1666, pp. 388–397. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48405-1_25
Kurosawa, K., Trieu Phong, L.: Leakage resilient IBE and IPE under the DLIN assumption. In: Jacobson, M., Locasto, M., Mohassel, P., Safavi-Naini, R. (eds.) ACNS 2013. LNCS, vol. 7954, pp. 487–501. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38980-1_31
Lewko, A., Rouselakis, Y., Waters, B.: Achieving leakage resilience through dual system encryption. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 70–88. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-19571-6_6
Lewko, A., Waters, B.: New techniques for dual system encryption and fully secure HIBE with short ciphertexts. In: Micciancio, D. (ed.) TCC 2010. LNCS, vol. 5978, pp. 455–479. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-11799-2_27
Li, J., Teng, M., Zhang, Y., Yu, Q.: A leakage-resilient CCA-secure identity-based encryption scheme. Comput. J. 59(7), 1066–1075 (2016)
Micali, S., Reyzin, L.: Physically observable cryptography. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 278–296. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_16
Naor, M., Segev, G.: Public-key cryptosystems resilient to key leakage. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 18–35. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_2
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 191–208. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14623-7_11
Qin, B., Chen, K., Liu, S.: Efficient chosen-ciphertext secure public-key encryption scheme with high leakage-resilience. IET Inf. Secur. 9(1), 32–42 (2015)
Shamir, A.: Identity-based cryptosystems and signature schemes. In: Blakley, G.R., Chaum, D. (eds.) CRYPTO 1984. LNCS, vol. 196, pp. 47–53. Springer, Heidelberg (1985). https://doi.org/10.1007/3-540-39568-7_5
Sun, S.-F., Gu, D., Liu, S.: Efficient leakage-resilient identity-based encryption with CCA security. In: Cao, Z., Zhang, F. (eds.) Pairing 2013. LNCS, vol. 8365, pp. 149–167. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-04873-4_9
Tomida, J., Abe, M., Okamoto, T.: Efficient functional encryption for inner-product values with full-hiding security. In: Bishop, M., Nascimento, A.C.A. (eds.) ISC 2016. LNCS, vol. 9866, pp. 408–425. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-45871-7_24
Yamada, S.: Adaptively secure identity-based encryption from lattices with asymptotically shorter public parameters. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 32–62. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-49896-5_2
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Proof of Lemmas
A Proof of Lemmas
To complete the proof of Theorem 1, we prove Lemmas 4, 6, 7, and 8.
Lemma 4

We introduce a lemma before proving Lemma 4.
Lemma 5
([19, Claim 6.7]). Let \(0< \rho < 1\) be a real. For a sequence of identities \(\mathbf {id}\in (\mathcal {ID})^{Q+1}\), and \(\mathcal {ABORT}\) be the event that the challenger aborts with added rules in \(\text {Game}_{2}\). For any fixed \(\mathbf {id}\),
Proof
(of Lemma 4). For a sequence of identities \(\mathbf {id}\in (\mathcal {ID})^{Q+1}\), we define \(\mathcal {Q}(\mathbf {id})\) as the event that \(\mathsf {A}\) uses the last entry in \(\mathbf {id}\) as the challenge and makes key generation queries and decapsulation queries for the remaining identities. Then, we have \(\sum _{\mathbf {id}\in (\mathcal {ID})^{Q+1}}\Pr [\mathcal {Q}(\mathbf {id})] = 1\). Let \(\delta (\mathbf {id}) = \Pr [\lnot \mathcal {ABORT}]\), and \(\delta _\mathrm {low}\) and \(\delta _\mathrm {up}\) be reals such that \(\delta _\mathrm {low}\le \delta (\mathbf {id}) \le \delta _\mathrm {up}\). Then, we have

The last inequality above follows from Lemma 3, since we have

and

From Lemma 5, we have \(\delta _\mathrm {up}- \delta _\mathrm {low}\le \eta _\mathrm {low}\rho /2\). Therefore, defining  , we obtain
, we obtain

\(\square \)
Lemma 6
For any PPT algorithm \(\mathsf {A}\), there exists a PPT algorithm \(\mathsf {D}\) such that

Proof
Let  be an XDLIN instance, where
be an XDLIN instance, where
Then, we build a PPT algorithm \(\mathsf {D}\) with input \((\left[ \mathbf {A} \right] _1,\left[ \mathbf {A} \right] _2,\left[ \mathbf {y} \right] _1)\) that simulates the IND-ID-lrCCA game with \(\mathsf {A}\) as follows.
-
Setup phase: \(\mathsf {D}\) generates \(\mathrm { pp }= \left( \left[ \mathbf {A} \right] _1,\left[ \mathbf {B}_0 \right] _1,\left[ \mathbf {B}_1 \right] _1,\ldots ,\left[ \mathbf {B}_m \right] _1,\left[ \mathbf {D} \right] _1\right) \) as same as the challenger, except that \(\mathsf {D}\) computes
$$\begin{aligned} \left[ \mathbf {B}_0 \right] _1&= \left[ \mathbf {A} \mathbf {R}_0 + \mathbf {I}_2 \right] _1, \\ \left[ \mathbf {B}_i \right] _1&= \left[ \mathbf {A} \mathbf {R}_i + h_i \mathbf {I}_2 \right] _1 \text { for } i = 1,\ldots ,m, \\ \left[ \mathbf {D} \right] _1&= \left[ \mathbf {A} \mathbf {E} \right] _1. \end{aligned}$$Finally \(\mathsf {D}\) sends \(\mathrm { pp }\) to \(\mathsf {A}\).
-
Query phase: \(\mathsf {D}\) answers for each query from \(\mathsf {A}\) as follows.
-
Key Generation query \(\mathrm { id }\). Assume that \(\beta _h(\mathrm { id }) \ne 0\). \(\mathsf {D}\) chooses
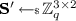 at random, computes
at random, computes 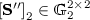 such that \(\left[ \beta _h(\mathrm { id }) \mathbf {S}'' \right] _2 = \left[ -\mathbf {A}\mathbf {S}' + \mathbf {A}\mathbf {E} \right] _2\), sets $$ \left[ \mathbf {S}_\mathrm { id } \right] _2 = \left[ \begin{pmatrix} \mathbf {S}' - \mathbf {R}_\mathrm { id }\mathbf {S}'' \\ \mathbf {S}' \end{pmatrix} \right] _2, $$
such that \(\left[ \beta _h(\mathrm { id }) \mathbf {S}'' \right] _2 = \left[ -\mathbf {A}\mathbf {S}' + \mathbf {A}\mathbf {E} \right] _2\), sets $$ \left[ \mathbf {S}_\mathrm { id } \right] _2 = \left[ \begin{pmatrix} \mathbf {S}' - \mathbf {R}_\mathrm { id }\mathbf {S}'' \\ \mathbf {S}' \end{pmatrix} \right] _2, $$and returns \(\mathrm { sk }_\mathrm { id }= \left[ \mathbf {S}_\mathrm { id } \right] _2\) to \(\mathsf {A}\).
-
Leakage query \((\mathrm { id }, f)\) and decapsulation query \((\mathrm { id }, \mathrm { ct })\). If \(\beta _h(\mathrm { id }) \ne 0\), then \(\mathsf {D}\) can generate \(\mathrm { sk }_\mathrm { id }\) as above. Furthermore, even in that case that \(\beta _h(\mathrm { id }) = 0\) (i.e., \(\mathrm { id }=\mathrm { id }^*\)), \(\mathsf {D}\) can generate \(\mathrm { sk }_\mathrm { id }\) by computing \(\mathbf {S}_\mathrm { id }\) such that
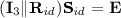 . Thus, \(\mathsf {D}\) can answer \(f(\mathrm { sk }_\mathrm { id })\) and \(\mathsf {Decap}(\mathrm { sk }_\mathrm { id }, \mathrm { ct })\) for any identity.
. Thus, \(\mathsf {D}\) can answer \(f(\mathrm { sk }_\mathrm { id })\) and \(\mathsf {Decap}(\mathrm { sk }_\mathrm { id }, \mathrm { ct })\) for any identity.
-
-
Challenge phase: \(\mathsf {D}\) generates the challenge \((\mathrm { ct }^*,K_b^*) = \left( (\left[ \mathbf {c}^* \right] _1,\left[ k_a \right] _T,\mathrm { sd }),K_b^*\right) \) as same as the challenger, except that \(\mathsf {D}\) computes
$$ \left[ \mathbf {c}^* \right] _1 = \left[ \begin{pmatrix} \mathbf {y} \\ \mathbf {R}_{\mathrm { id }^*}^\top \mathbf {y} \end{pmatrix} \right] _1 $$instead of \(\left[ \mathbf {c}^* \right] _1 = \left[ \mathbf {F}_{\mathrm { id }^*}^\top \mathbf {r} \right] _1\). Then, \(\mathsf {D}\) returns \((\mathrm { ct }^*,K_b^*)\) to \(\mathsf {A}\).
Finally, \(\mathsf {D}\) outputs \(\gamma = [b = b']\) where  is the output of \(\mathsf {A}\).
is the output of \(\mathsf {A}\).
We will show that the distribution of \((\mathrm { ct }^*, K_b^*)\) is the same as the challenge in \(\text {Game}_{4}\) if \(\mathbf {y} = \mathbf {A}^\top \mathbf {r}^*\), while if \(\mathbf {y}\) is a random it is the same as that in \(\text {Game}_{5}\) with overwhelming probability. First suppose that \(\mathbf {y} = \mathbf {A}^\top \mathbf {r}^*\). In this case,

showing that \((\mathrm { ct }^*, K_b^*)\) is the challenge in \(\text {Game}_{4}\). Next suppose that \(\mathbf {y}\) is random in  . It suffices to prove that
. It suffices to prove that  is also random in
is also random in  even given \(\mathbf {A}\),
even given \(\mathbf {A}\),  , and \(\mathbf {y}\). It is easy to see that
, and \(\mathbf {y}\). It is easy to see that
Therefore, \(\mathbf {z}\) is random because \(\mathbf {V}\) is of full rank with probability \(1-1/q\). Hence, \(\left[ \mathbf {c}^* \right] _1\) is random as expected.
Thus, \(\text {Game}_{4}\) and \(\text {Game}_{5}\) are indistinguishable under the XDLIN assumption, so that we have Eq. (17). \(\square \)
Lemma 7

Proof
We assume that all decapsulation queries are made after the challenge phase, but a similar (but slight simpler) argument can be used if \(\mathsf {A}\) makes queries before the challenge phase. Suppose that \((\mathrm { id }^*,\mathrm { ct }= (\left[ \mathbf {c} \right] _1,\left[ t \right] _T,\mathrm { sd }))\) is the first decapsulation query such that \(\mathrm { id }= \mathrm { id }^*\) and the condition at line 13 in Fig. 1 is evaluated. Let  , where
, where  . Then, we have
. Then, we have

where \(k_a\) is computed at line 11 in Fig. 1. From the supposition, we can assume that \(\alpha \ne \alpha ^*\), \(\mathbf {c}^*\) is chosen uniformly at random, and \(\left[ \mathbf {c} \right] _1\) is invalid for \(\mathrm { id }^*\). Hence, the matrix \(\mathbf {M}\) is of full rank with probability at least \(1-1/q\), that implies that the distribution of \(k_a\) is random and independent from \(\mathbf {D}\) and \(k_a^*\). In addition to \(\mathbf {D}\) and \(k_a^*\), \(\mathsf {A}\) knows at most \(\ell \) bit leakage  and n bit challenge session key \(K_b^*\) that is probable to provide information on the value of \(k_a\) to \(\mathsf {A}\). Let \(K_a\), F, and I denote random variables induced by \(k_a\),
and n bit challenge session key \(K_b^*\) that is probable to provide information on the value of \(k_a\) to \(\mathsf {A}\). Let \(K_a\), F, and I denote random variables induced by \(k_a\),  , and \(({\mathbf D}, k_a^*)\), respectively. Given \(k_a\),
, and \(({\mathbf D}, k_a^*)\), respectively. Given \(k_a\),  , and \(({\mathbf D}, k_a^*)\) that \(\mathsf {A}\) knows, we have
, and \(({\mathbf D}, k_a^*)\) that \(\mathsf {A}\) knows, we have
from Lemma 1 and the above discussion. Thus, for any \(k_a\), we have \(\Pr [K_a=k_a] \le 2^{\ell +n}/q\). Therefore, in the first evaluation of line 11, the condition \(t=k_a\) is satisfied with probability at most \({2^{\ell +n}}/{q}\). Now assuming \(t=k_a\) is not satisfied, the number of possible \(k_a\) decreases one. So, in the i-th evaluation of line 11, the probability that \(t=k_a\) holds is at most \(2^{\ell +n}/(q-i+1)\), in the case that \(t=k_a\) is not satisfied in all previous evaluations. From the above discussion, we have

From Eq. (2), we obtain Eq. (18). \(\square \)
Lemma 8

Proof
In \(\text {Game}_{9}\), the challenger returns \(\bot \) to \(\mathsf {A}\) at line 13 in Fig. 1. Hence, \(\mathsf {A}\) does not learn any information on \(k_s^*\) via the decapsulation oracle, since \(\mathsf {A}\) can only get decapsulation results of valid ciphertexts. Now, \(\mathsf {A}\) knows \(\mathbf {D}\), \(k_a^*\), and  as information about \(k_s^*\). Then, we show that the min-entropy of \(k_s^*\) is at least \(\log _2{q} - \ell \) with probability at least \(1-1/q\).
as information about \(k_s^*\). Then, we show that the min-entropy of \(k_s^*\) is at least \(\log _2{q} - \ell \) with probability at least \(1-1/q\).
First, we have
and then

The matrix \(\mathbf {N}\) is of full rank with probability at least \(1-1/q\), since \(\alpha ^*\ne 0\) and \(\left[ \mathbf {c}^* \right] _1\) is uniformly at random. Then, the distribution of \(k_s^*\) is random and independent from \(\mathbf {D}\) and \(k_a^*\). In addition to \(\mathbf {D}\) and \(k_a^*\), \(\mathsf {A}\) knows at most \(\ell \) bit leakage  that is probable to provide information on the value of \(k_s^*\) to \(\mathsf {A}\). Let \(K_a\), D, and F denote random variables induced by \(k_s^*\), \((\mathbf {D},k_a^*)\), and
that is probable to provide information on the value of \(k_s^*\) to \(\mathsf {A}\). Let \(K_a\), D, and F denote random variables induced by \(k_s^*\), \((\mathbf {D},k_a^*)\), and  respectively. Given \(k_s^*\), \((\mathbf {D},k_a^*)\), and
respectively. Given \(k_s^*\), \((\mathbf {D},k_a^*)\), and  that \(\mathsf {A}\) knows, we have
that \(\mathsf {A}\) knows, we have
from Lemma 1 and the discussion when ignoring  . Hence \(\mathsf {Ext}(K_s^*, \mathrm { sd }^*)\) is statistically indistinguishable from an n bits random string because \(\mathsf {Ext}\) is a \((\log _2{q} - \ell )\)-randomness extractor. Therefore, we have Eq. (19). \(\square \)
. Hence \(\mathsf {Ext}(K_s^*, \mathrm { sd }^*)\) is statistically indistinguishable from an n bits random string because \(\mathsf {Ext}\) is a \((\log _2{q} - \ell )\)-randomness extractor. Therefore, we have Eq. (19). \(\square \)
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Tomita, T., Ogata, W., Kurosawa, K. (2019). CCA-Secure Leakage-Resilient Identity-Based Key-Encapsulation from Simple (Not \(\mathtt {q}\)-type) Assumptions. In: Attrapadung, N., Yagi, T. (eds) Advances in Information and Computer Security. IWSEC 2019. Lecture Notes in Computer Science(), vol 11689. Springer, Cham. https://doi.org/10.1007/978-3-030-26834-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-26834-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-26833-6
Online ISBN: 978-3-030-26834-3
eBook Packages: Computer ScienceComputer Science (R0)


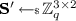 at random, computes
at random, computes 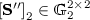 such that
such that 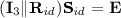 . Thus,
. Thus,