Abstract
Leakage-resilient encryption is a powerful tool to protect data confidentiality against side channel attacks. In this work, we introduce a new and strong leakage setting to counter backdoor (or Trojan horse) plus covert channel attack, by relaxing the restrictions on leakage. We allow bounded leakage at anytime and anywhere and over anything. Our leakage threshold (e.g. 10000 bits) could be much larger than typical secret key (e.g. AES key or RSA private key) size. Under such a strong leakage setting, we propose an efficient encryption scheme which is semantic secure in standard setting (i.e. without leakage) and can tolerate strong continuous leakage. We manage to construct such a secure scheme under strong leakage setting, by hiding partial (e.g. 1%) ciphertext as secure as we hide the secret key using a small amount of more secure hardware resource, so that it is almost equally difficult for any adversary to steal information regarding this well-protected partial ciphertext or the secret key. We remark that, the size of such well-protected small portion of ciphertext is chosen to be much larger than the leakage threshold. We provide concrete and practical examples of such more secure hardware resource for data communication and data storage. Furthermore, we also introduce a new notion of computational entropy, as a sort of computational version of Kolmogorov complexity. Our quantitative analysis shows that, hiding partial ciphertext is a powerful countermeasure, which enables us to achieve higher security level than existing approaches in case of backdoor plus covert channel attacks. We also show the relationship between our new notion of computational entropy and existing relevant concepts, including All-or-Nothing Transform and Exposure Resilient Function. This new computation entropy formulation may have independent interests.
A full version [28] is available at https://eprint.iacr.org/2018/846.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Leakage resilient encryption
- Secret sharing
- Information dispersal algorithm
- Information-theoretic security
- Side channel attack
- Covert channel attack
- Subliminal channel
- Kolmogorov complexity
1 Introduction
Leakage resilient cryptography has been studied for over a decade, aiming to counter side channel attacks, among other goals. Existing works on leakage resilient cryptography typically impose some restrictions on when, where, or what can be leaked. Some work assumes that there exits a leakage-free setup phase. Some works assume there exists a secure hardware device, such that any computation inside this secure device is leakage-free. If some secret key is stored in such secure device and never leaves from it, then such secret key is assumed to be leakage-free. Some works only allow leakage on secret key. Furthermore, some works consider bounded leakage with a very small upper bound—\(O(\mathtt {Poly}(\log \lambda ))\) where \(\lambda \) is the security parameter.
1.1 Background in Existing Leakage Models
1.1.1 Bounded Retrieve Model
The bounded retrieve model [2, 3, 13, 15] assumes the total amount of leaked information during the lifetime of the attacked system, is upper bounded by a constant \(\ell \), which could be as large as gigabytes. An existing approach [3, 13] is to purposely make the shared secret key size significantly larger than the leakage upper bound—\(\ell \) (e.g. \(\ge 2\ell + \lambda \) where \(\lambda \) is the security parameter). In order to make the computation as fast as the case of short secret key, this approach assumes a leakage-free phase, during which, one party (say, Alice) can randomly extract a short session key from the large shared secret key using a random seed. The other party (say, Bob) of communication can re-generate the same short session key from the same shared large secret key after receiving the same random seed.
It is easy to see, under continuous bounded leakage setting, any static secret key can be leaked one bit by one bit, and pseudorandomness technique cannot be applied directly since short seed could be (partially) leaked. Furthermore, we allow \(\mathcal {O}(\lambda )\) bits leakage such that leakage threshold could be larger than secret key size (e.g. the short session key in the above paragraph), thus the whole block cipher key (e.g. 128 bits AES key) could be leaked. Therefore, bounded retrieve model does not satisfy our goal.
1.1.2 A Leakage-Free Time Period During the Computation Process of Cryptography Primitive
Alwen, Dodis and Wichs [2] proposed several leakage resilient cryptography primitives with flexible (and possibly very large) key size. A key idea in their authenticated key agreement scheme, is: (1) Generate many keys in the setup; (2) and during a leakage-free time period, the sender and receiver will randomly sample a subset of keys, and use them to authenticate each other; and then establish a short shared session key. As long as a constant fraction of all keys are unknown to the adversary after bounded leakage, a random subset of keys contains at least one unknown key with very high probability. After that, standard cryptography primitives are applied with the short secure session key (e.g. AES).
In our leakage setting, there will be no leakage-free time period and any short value (e.g. AES key) could be leaked. So we have to seek new approaches.
1.1.3 Secret Key Never Leaves from Secure Hardware Device
The computation power of secure hardware devices (e.g. Trusted Platform Module) may not be able to match the power of desktop Intel/AMD CPU. Furthermore, there seems no evidence to show that the vendors of secure hardware device are more trusted than vendors of other component (e.g. CPU, GPU, RAM, hard disk, OS, web browser, virtual machine software, etc.) in a computer system.
1.1.4 Randomness Extractor
One may consider to extract a short block cipher (e.g. AES) key from a long secret key and then encrypt the message using the short block cipher directly. Assuming leakage only occurred before the randomness extractor was applied, (e.g. as the setting of [3, 13]), this method will work. But in our setting, we do not make such assumption, and instead we allow bounded leakage at any time.
1.1.5 Memoryless Leakage Oracle
An essential difference between leakage oracle in side channel attack in related works and leakage oracle in Trojan horse malware plus covert channel attack in this paper, is that, whether the leakage oracle has cache memory and is allowed to access history data. Some recent works in leakage resilient cryptography [6, 7, 23] assumes that: (1) for each invocation of cryptography primitive, the leakage threshold is smaller than secret key size; and (2) leakage oracle only takes input from current status of the cryptography computation, and is not allowed to access historical status. They can achieve security by refreshing the secret key frequently (together with other techniques). Imagine a simplified example [23]: To encrypt the i-th message, one may adopt a fresh 256-bit encryption key \(k_i := \mathtt{SHA256}(k_{i-1})\), and the adversary is allowed to learn only a single bit \(\mathcal {L}(k_i) \in \{ 0,1 \}\) over the key \(k_i\). With all leaked information \(\{ \mathcal {L}(k_j): j \in [0, i] \}\), a polynomial-time adversary seems not be able to learn some useful knowledge about any secret key. However, in case of Trojan horse plus covert channel attack in this paper, the Trojan horse malware may keep an old key \(k_0\) in a local cache memory, and send out one bit per every invocation of encryption scheme via covert channel. So after encrypting \(|k|=256\) messages, all of 256 bits of \(k_0\) could be sent out to a remote adversary, who can compute every \(k_i\) from \(k_0\). With all ciphertexts (which can be obtained via eavesdropping, without resorting to leakage oracle), the adversary can decrypt and recover all plaintexts. Thus 256 bits leakage leads to exposure of everything—all plaintexts and (future) secret keys. Our new security formulation in this work is aiming to prevent such kind of leakage amplification.
It will be interesting to study the leakage resilient cryptography with adversary who has limited leakage bandwidth (say \(\ell \) bits per invocation of crypto primitive) and limited cache memory (say w bits memory). In this work, we actually do not assume any upper bound in the size of cache memory. Since covert channel with large bandwidth and/or Trojan horse with large cache memory, may be more easily captured or prevented by existing solution (e.g. anti-virus software and intrusion detection system, Trojan-Resilient hardware [9, 16]), it is reasonable to put some small upper bound in values of \(\ell \) and w. We leave this as an open problem.
1.2 Our Contributions
The main contributions of this work can be summarized as below.
1.2.1 New Leakage Setting
Since existing leakage settings does not fit for our goal, we present a new strong leakage model, to capture the threat of backdoor or Trojan horse and covert channels in computer hardware/software systems. We allow bounded (e.g. 10000 bits) leakage at anytime and anywhere and over anything, with only two restrictions on the adversary: (1) the adversary algorithms are efficient (probabilistic polynomial time); (2) the bandwidth of the covert channel is bounded from the above. By our knowledge, all existing works designed for leakage settings in Sect. 1.1 are trivially broken under our leakage setting, since the Trojan horse could observe every step of computation of the victim program (e.g. an encryption program) and then steal the entire short private key. We emphasize that, the white box cryptography [5, 18] using program obfuscation, which claims to protect secret key from attackers with direct control of the encryption device, is prohibitively impractical, even for a simple function [12].
1.2.2 Notion of Steal-Entropy
We propose a new notion called “steal-entropy”, as a sort of computational version of Kolmogorov complexity. With this “steal-entropy”, we quantitatively analyse the advantage of our approach over existing works. Our formulation is non-trivial and has to resolve several important issues: (1) Unlike Shannon-Entropy, Yao-Entropy and Hill-Entropy are defined over distribution of random variable, and Kolmogorov complexity is defined over string, our steal-entropy will be defined over an algorithm which converts the distribution of input random variable to the distribution of output random variable. (2) Statistical or computational indistinguishability notion (e.g. semantic security under CPA/CCA/CCA2 attack mode) is inappropriate in our leakage setting, since a single bit of arbitrary leakage will help an adversary to win the guess-game trivially. (3) Kolmogorov complexity is uncomputable in general, but in our formulation, we should avoid to define any uncomputable function. As a result, unlike existing variant formulations of entropy, it is hard to define our steal-entropy as a single scalar value (More discussion is available in our full version). Instead, we will give an upper bound and a lower bound for the steal-entropy of a given algorithm. To show a program has poor steal-entropy, we need provide a small upper bound on the steal-entropy of this program; to show a program has high steal-entropy, we need provide a large lower bound on the steal-entropy of this program.
1.2.3 Construction
We propose an efficient encryption scheme and demonstrate that hiding partial ciphertext could be a powerful tool to defeat strong leakage attack. We construct our encryption scheme using Vandermonde matrix and evaluate the steal-entropy of the proposed scheme without relying on any hard problem assumption. Informally speaking, our encryption scheme will ensure that, without complete ciphertext, the attacker obtains very limited information about the plaintext, even if the attacker has stolen a bounded amount of message (e.g. the entire short private key) of his/her choice. We will compare our solution with some related approaches, including All-or-Nothing Transform and White-Box Cryptography, both of which could not satisfy our goal.
The proposed solution will be used to construct a “virtually isolated network” [29]. We discuss details later in Sect. 2.
1.3 Organizations
The rest of this paper is organized in this way: Sect. 2 gives an overview of our work, including our leakage setting, formulation of steal-entropy, and our proposed construction of leakage/steal-resilient encryption scheme. In addition to the related works already discussed in Sects. 1 and 2, Sect. 3 discusses more related works. We present our formal formulation of steal-entropy in Sect. 4, propose and analyse our encryption scheme in Sect. 5. We conclude this paper in Sect. 6. A full version with more details is available online [28].
2 Overview of Our Work
2.1 Our Leakage Setting
2.1.1 Motivation of New Leakage Setting
In this paper, we aim to counter not only side channel attack but also covert channel attack. Nowadays, computer systems become so complex and consist of a lot of software/hardware components which are designed, manufactured and sold by various companies from various countries. It is definitely not a trivial task for PC users to check whether some backdoor program or malware (e.g. Trojan horse) has been planted inside his/her PC hardware/software system. The well-known “Dual Elliptic Curve Deterministic Random Bit Generator” (Dual_EC_DRBG) backdoorFootnote 1 demonstrates that the potential threat from backdoor is not that far away from every computer user. Another serious threat is software Trojans horse or even hardware Trojan horseFootnote 2. The backdoor or Trojan horse malware may observe the victim’s computer system to gather information and send collected (possibly compressed) information out via a covert channel or subliminal channel.
Facing such threats from backdoor and Trojan horse, in this work, we have to revise the existing leakage setting: (1) Theoretically, backdoor or Trojan horse programs could be planted by some software/hardware vendor and they exist in victim’s computer from the very beginning. So it might not be appropriate to assume a leakage-free time period. (2) Possibly, the backdoor program might be planted by vendors of the secure hardware device and the assumption of leakage-free secure hardware device is hard to validate. (3) The backdoor or Trojan horse malware may have their own storage buffers, so history data can be buffered and then leaked 1 bit by 1 bit via the covert channel (thus Pereira, Standaert and Vivek [23] would be broken trivially as discussed in Sect. 1.1.5).
2.1.2 New Leakage Setting
In general, we allow efficient leakage with bounded bandwidth at anytime and anywhere and over anything. The only two restrictions on leakage are: (1) The leakage amount of each encryption (i.e. the bandwidth of covert channel) is bounded (e.g. \(\mathcal {O}(\lambda )\)). In this paper, we are interested in medium value of leakage threshold, e.g. tens of thousands bits, which is much larger than typical private key size (e.g. AES key and RSA private key). (2) The backdoor or Trojan horse program (i.e. the leakage function) is computationally bounded (e.g. polynomial time algorithm). Our setting is closer to study of memory leakage resilient cryptography, and does not follow the assumption that only computation leaks information [22].
Recall that, in most, if not all, leakage-resilient cryptography research works, an adversary has two different methods to obtain desired information:
-
A cheap method to obtain a large amount of weakly protected information, for example, eavesdropping ciphertext on communication link.
-
An expensive method to obtain a small amount of strongly protected information, for example, using side channel attack or Trojan horse malware plus covert channel attack to obtain partial or full information of the short secret key.
Typically in existing works, an adversary is assumed to obtain full information of ciphertext using the cheap method (e.g. eavesdropping), meanwhile subject to several restrictions on obtaining information of short secret key (e.g. assumed leakage-free time period or hardware device). Unlike existing works, in this paper, we impose minimum restrictions on information leakage, and assume that a small part (e.g. 1% or 0.1%) of ciphertextFootnote 3 is as strongly protected as the short secret key, so that the adversary has to resort to the expensive method (e.g. Trojan horse and covert channel) to obtain this part of ciphertext. Next, we will support this assumption with real world examples.
Secure Storage Device. For data storage, we assume there are two categories of storage: one with small capacity is relatively more expensive, in term of unit price, but much more secure; the other with large capacity is cheaper but insecure. In case that a user wish to backup large size sensitive historical data in cloud storage server, but did not trust the cloud in data confidentiality. Then this user’s local offline storage device, which is physically disconnected from any computers and Internet, could be an example of the former, and the cloud storageFootnote 4 could be an example of the latter.
Secure Communication Link. For data transmission, we assume there exist two categories of communication channels, one with small bandwidth is very expensive but much more secure, such that an adversary cannot obtain the transmitted data with low cost (e.g. eavesdropping); the other with large bandwidth is cheap but insecure, such that an adversary can obtain all transmitted data with low cost. The example of former could be satellite link (or even neutrinos communication in the future), which is relatively more difficult to eavesdrop, and the example of latter could be Internet. Another example is “virtually isolated network”Footnote 5, recently proposed by Xu and Zhou [29], which is a hybrid network with two communication channels: one is a physically isolated network with small bandwidth, and the other is Internet with large bandwidth. Their work [29] combines these two channels with unidirectional network links (a.k.a data diode or air gap), so that the isolated network will be still always physically isolated from Internet.
Our strategy is to enhance security level of the large amount of cheap but insecure hardware resource by leveraging on small amount of expensive but more secure hardware resource, essentially creating a hybrid effects in security. We aim to prevent the adversary from eavesdropping full information of our ciphertext.
2.2 Notion of Steal-Entropy
Unlike previous leakage formulation, we attempt to formalize security in leakage setting from a different angle. We try to answer a very important question:
“At least how many bits should the adversary steal in order to obtain the desired secret information?”
In this work, we are concerning how many bits the adversary has to obtain using the expensive method, in order to obtain full or partial information of the plaintext. Informally, we may call this “minimum but sufficient number of leaked/stolen bits” which will lead to compromise of secret plaintext, as the steal-entropy of the encryption algorithm.
Let \(\mathsf {P}\) (e.g encryption algorithm/program) denote the victim algorithm or program. In our formulation, an adversary chooses two algorithms, denoted with steal algorithm \(\mathsf {S}\) and recovery algorithm \(\mathsf {R}\). The steal algorithm \(\mathsf {S}\) is given oracle access to the whole computation process of \(\mathsf {P}\), including any internal states (e.g. secret keys, random seeds, input and any computation steps). Then the steal algorithm \(\mathsf {S}\) is allowed to pass a short message, which is at most \(\ell \) bits, to the recovery algorithm \(\mathsf {R}\), which attempts to output desired secret information. If the recovery algorithm \(\mathsf {R}\) is able to output the desired secret information with probability close to 1, with value of \(\ell \) much smaller than the size of desired secret information, then we say the victim algorithm \(\mathsf {P}\) has very low steal-entropy rate. In this work, we are interested in medium value of leakage threshold \(\ell \) (e.g. tens of thousands), which is larger than typical secret key length, but could be much smaller than typical ciphertext length. Our notion of “steal-entropy” could be treated as a computation version of Kolmogorov complexity.
2.2.1 Steal-Entropy in Input or Output
Pseudorandom number generators, pseudorandom function and encryption are important cryptography primitives applied to protect data confidentiality. For an algorithm \(\mathsf {P}\) similar to pseudorandom number generator and pseudorandom function, we are interested to ask a question: Assuming a Trojan horse malware is observing the computation process of algorithm \(\mathsf {P}\) upon a randomly chosen input x, at least how many bits should the Trojan horse malware steal and send out, in order to allow a remote attacker to recover the output \(\mathsf {P}(x)\) of the algorithm \(\mathsf {P}\)? To address this question, we define a notion called “Steal-Entropy of an algorithm in Output”. Due to space constrain, we will leave the formal definition of this notion in the full version of this paper.
For algorithm \(\mathsf {P}\) similar to encryption scheme, we are interested to ask another question: Assuming a Trojan horse malware is observing the computation process of algorithm \(\mathsf {P}\) upon a randomly chosen input x, at least how many bits should this Trojan horse malware steal and send out, in order to allow a remote attacker to recover the input x, where this remote attacker has access to the outputFootnote 6 \(\mathsf {P}(x)\)? To address this question, we define a notion called “Steal-Entropy of an algorithm in Input”. In addition, to deal with partial information protection, we define a notion called “Strong Steal-Entropy of an algorithm”.
2.2.2 Relation with Existing Similar Notions
We also formally analyze the differences between our notion of steal-entropy with existing similar notions, including Yao-Entropy [30], Hill-Entropy [19], Information Dispersal Algorithm [24], All-or-Nothing Transform [25], and Exposure Resilient Function [10]. We manage to separate our proposed steal-entropy from all of these existing formulations. More details are in our full version [28].
2.3 Our Approach
When the leakage threshold \(\ell \) is larger than typical secret key size, most existing encryption schemes and leakage resilient encryption schemes (which only tolerates leakage upto \(O(poly \log \lambda ) < \lambda \) bits, where \(\lambda \) is the security parameter) would fail to protect data confidentiality, since in typical setting, an adversary could obtain all ciphertext with low cost (e.g. eavesdropping), and the secret decryption key could be stolen by Trojan horse malware and delivered to the remote adversary via covert channel.
Facing such stringent threat of medium size of arbitrary information leakage, two possible directions are: (1) Construct novel encryption scheme with larger flexible key size, say the encryption/decryption key size could be a user-tunable parameter, and range from hundreds bits to hundreds of thousands bits or even more. We will report our work in this direction in a separate paper. We remark that Alwen, Dodis and Wichs [2] does not satisfy our purpose, since this work [2] eventually extracted a short session key from arbitrary large size long term secret key, where this extracted short session key could be stolen under our leakage setting. (2) Break the assumption that the adversary could easily obtain all ciphertext. Indeed, this work will attempt to hide a small portion of ciphertext using more secure hardware resource, so that the adversary has to resort to the expensive method to steal information about this small portion of ciphertext, in a similar way that he/she steals the secret key.
2.3.1 Randomness Source
Any static secret information might be stolen one bit by one bit, if backdoor or Trojan horse exists. To defeat continuous leakage/steal with buffer storage, we have to keep investing more and more randomness. However, it is expensive to generate cryptographically secure randomness. In our solution, we will exploit the fact that plaintext itself is naturally a sort of random source to the view of adversary, saving the cost to generate true randomness. We protect a small portion of the ciphertext using more secure hardware resource, so that this portion of ciphertext actually acts as another “secret key”, which is derived from the plaintext and will change naturally with plaintext, to the view of adversary.
2.4 Our Construction
Our leakage setting provides much more freedom and power to adversary, compared to existing works on leakage-resilient cryptography. Consequently, the two very important classical tools, namely computational indistinguishability and (statistical or computational) randomness extractor, are hardly to be applied under our formulation. In this work, we have to resort to information theory techniques.
Definition 1
(Blockwise Uniform Distribution). Let \(\varvec{\varvec{y}} = (\mathbf {y}_1, \mathbf {y}_2, \cdots , \mathbf {y}_n)\), where \(\mathbf {y}_i \in \{ 0,1 \}^{\rho }\) for each \(i \in [1, n]\). We say \(\varvec{\varvec{y}}\) follows \((\zeta , \rho )\)-Blockwise-Uniform Distribution, if for any subset \(S = \{ i_1, i_2, \cdots , i_{\zeta } \} \subset [1, n]\) with \(|S| = \zeta \) and \(i_1< i_2< i_3< \cdots < i_{\zeta }\), we have the joint Shannon-entropy
That is, any subset of \(\zeta \) distinct blocks \(\mathbf {y}_i\) will have joint Shannon entropy equal to their total bit-length (i.e. entropy rate equal to 1).
Remark 1
When \(\rho =1\) and \(\zeta =n\), then \((\zeta , \rho )\)-Blockwise-Uniform Distribution is identical with uniform distribution.
In this work, we will construct an invertible algorithm \(\mathsf {P}\) using Vandermonde matrix, such that its inverse algorithm \(\mathsf {P}^{-1}\), satisfies this property:
Property 1
Let \(\mathtt {Ctx}_0\) and \(\mathtt {Ctx}_1\) be the small share and large share of ciphertext, and assume the bit-length \(|\mathtt {Ctx}_1| = \tau \cdot |\mathtt {Ctx0}| = \tau \rho \zeta \). If \(\mathtt {Ctx_0}\) is independently and uniformly randomly distributed over \(\{ 0,1 \}^{\rho \zeta }\), then the output \( x = \mathsf {P}^{-1}(\mathtt {Ctx}_0, \mathtt {Ctx}_1)\) follows \((\zeta , \rho )\)-Blockwise-Uniform Distribution, regardless of value of \(\mathtt {Ctx}_1\) (e.g. this value could be fixed to any given bit-string from its domain).
Suppose somehow an attacker is able to output \(\zeta \) bits among \(x_i\)’s, say \(x_{i_j}\), \(j \in [1, \zeta ]\). Then these \(\zeta \) bits \(x_{i_j}\)’s will reside in at most \(\zeta \) distinct \(\rho \)-bit blocks in bit-string x. Since any subset of \(\zeta \) blocks of x will have Shannon entropy rate equal to 1 (i.e. entropy equal to the bit-length), the collection of these \(\zeta \) bits \(x_{i_j}\)’s will have exactly \(\zeta \) bits Shannon entropy. Therefore, the adversary has to steal at least \(\zeta \) bits message via the covert channel, as desired. Apparent, the above proof is not tight with a multiplicative loss of factor \(\rho \). We leaf the tight proof with better security parameters in future work.
3 Related Works
The related works in leakage resilient cryptography have been discussed in Sect. 1.1. Here we discuss other related works.
Symmetric encryption scheme (e.g. AES, BlowfishFootnote 7, and Triple DESFootnote 8.) could be the most widely adopted cryptographically secure primitive to protect data confidentiality, especially for large volume of data. AES [11] is a typical example of symmetric encryption scheme, and has been actively adopted in industry and research area due to its security and efficiency for more than one decade.
In additional to encryption techniques, another well-known cryptographic primitive that can be used to protect data confidentiality is “secret-sharing” scheme invented by Shamir [26]. Compared to encryption scheme (e.g. AES [11]) which can only achieve conditional security, secret-sharing scheme may achieve unconditional security (also known as information-theoretic security), assuming the adversary cannot collect sufficient number of shares.
Despite its strong security, Shamir’s secret sharing scheme has significant drawbacks when protecting data confidentiality: (1) for (t, n)-secret sharing scheme, the storage overhead is as large as \((n-1)\) times of size of the secret (i.e. the plaintext to be protected); (2) the reconstruction [21] (or decoding) process is not as efficient as DES or AES.
Rabin [24] proposed “information dispersal algorithm” with zero storage overhead, such that the sum of sizes of all shares is equal to the size of secret message size. His solution is conceptually simple: Let row vector \(\varvec{\varvec{m}} = (m_0, m_1, \ldots , m_{n})\) be the secret message. Choose an invertible n by n matrix \(\mathbf {T}\) with inverse matrix \(\mathbf {T}^{-1}\). By multiplying row vector \(\varvec{\varvec{m}}\) with matrix \(\mathbf {T}\), we obtain the n shares \(\varvec{\varvec{c}} = (c_0, c_1, \ldots , c_{n-1}) = \varvec{\varvec{m}} \times \mathbf {T}\). Accordingly, the original secret message \(\varvec{\varvec{m}}\) can be recovered by matrix multiplication \(\varvec{\varvec{m}} = \varvec{\varvec{c}} \times \mathbf {T}^{-1}\). Othman and Mokdad [8] proposed to protect communication confidentiality by sending each share of message in distinct network path from the same sender to the same receiver.
Alternatively, Krawczyk [20] attempted to make each share shortened, by dividing ciphertext of the long secret message into n pieces, and then apply Shamir’s secret sharing scheme over the encryption key. Thus, the storage overhead is linear in short encryption key size and is a fraction of secret message size.
4 Steal-Entropy: How Many Bits Should Be Stolen to Recover the Secrete Information?
In this section, we propose the notion of “Steal-Entropy”. Unlike traditional entropy concepts (e.g. Shannon-Entropy, Yao-EntropyFootnote 9, Hill-Entropy, etc) which are defined over random variable with a certain distributions, “steal-entropy” will be defined over algorithms which convert input distribution to output distribution. Our notion of “steal-entropy” could be considered as a computational version of Kolmogorov Complexity [4], which is quoted in full version.
4.1 Steal-Entropy of an Algorithm in Input
Definition 2
(Steal-Entropy of an Algorithm in Input). Let \(\mathsf {P}: \{ 0, 1 \}^{n} \rightarrow \{ 0,1 \}^{m}\) be a deterministicFootnote 10 single-input algorithm. Let \(\epsilon \in [0, \frac{1}{4})\). Let \(\mathcal {A}\) be a t-adversary associated with a pair of algorithms \( ({{\mathsf {S}}},\ {{\mathsf {R}}})\), such that
-
both the steal (or stealage) algorithm \({{\mathsf {S}}}\) and the recovery algorithm \({{\mathsf {R}}}\) are probabilistic algorithms within time t, and
-
for any non-negative integer \(\ell \), the steal algorithm
$$ {{\mathsf {S}}}^{\mathcal {O}(\mathsf {P}(x))}(\ell ) \in \{ 0,1 \}^{\le \ell } \setminus \{ \texttt {EmptyString} \} $$with oracle access to \(\mathsf {P}\), is allowed to observe all internal states during computation process of algorithm \(\mathsf {P}\) upon an input x, and outputs at most \(\ell \) bits non-empty steal-message, and
-
the recovery algorithm \({{\mathsf {R}}}\) takes as input the value \(\mathsf {P}(x)\) and the steal-message generated by \({{\mathsf {S}}}(\ell )\), and attempts to guess the value x.
We make the following definitions.
-
We define the advantage of \(\mathcal {A}\) against \(\mathsf {P}\) w.r.t. input \(x \in \{ 0,1 \}^{n}\) as below
$$\begin{aligned} \mathsf {Adv}_{\mathcal {A}(\ell ), \mathsf {P}}^\mathtt{{in}}(x) = \Pr \left[ {\mathsf {R}}\left( {{\mathsf {S}}}^{\mathcal {O}\big (y \leftarrow \mathsf {P}(x) \big )} (\ell ),\ y \right) = x \right] \end{aligned}$$(2)where the probability is taken over all random coins of algorithms \({{\mathsf {S}}}\) and \({\mathsf {R}}\).
-
We say the infimum of Steal-Entropy in Input of algorithm \(\mathsf {P}\) is at least \(\xi \), denoted as \(\inf {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}) \ge \xi \), if for any t-adversary \(\mathcal {A}\), for any non-negative integer \(\ell \le \xi \),
 (3)
(3) -
We say the supremum of Steal-Entropy in Input of algorithm \(\mathsf {P}\) is at most \(\xi \), denoted as \(\sup {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}) \le \xi \), if for some t-adversary \( \mathcal {A}\),
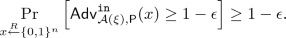 (4)
(4) -
We say \({{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_0) \ge {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_1) \) (or equivalently \( {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_1) \le {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_0) \)), if the following two equations hold
$$\begin{aligned} \inf {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_0) \ge \inf {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_1); \sup {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_0) \ge \sup {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_1). \end{aligned}$$(5) -
We say \({{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_0) \gg {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_1) \) (or equivalently, \( {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_1) \ll {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_0) \)), if the following equation holds
$$\begin{aligned} \inf {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_0) \ge \sup {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}_1). \end{aligned}$$(6)
Proposition 1
If \(\mathsf {P}\) is an invertible algorithm, and the inverse algorithm \(\mathsf {P}^{-1}\) has running time \(\le t\), then \(\inf {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}) = \sup {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}) = 0\).
When the encryption/decryption key is fixed, an encryption algorithm \(\mathsf {Enc}\) is an invertible algorithm from plaintext to ciphertext. Before any information leakage, an adversary may have knowledge of the whole family \(\{ \mathsf {Enc}_{k} \}_{k \leftarrow \mathsf {KGen}(1^{\lambda })}\) and do not know which one is picked from this family of permutation algorithms. By stealing the key k, an adversary is able to recover plaintext from ciphertext. This simple fact is summarized as below.
Proposition 2
For any PPT encryption scheme \((\mathsf {KGen}, \mathsf {Enc}, \mathsf {Dec})\) and for any key k generated by \(\mathsf {KGen}\), we have \(\sup {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}\big (\mathsf {Enc}_{k}\big ) \le |k|, \text { where } \epsilon =0, \text { and } t= poly(\cdot ).\)
4.2 Discussion
An interesting question is to evaluate the steal-entropy for classical hard problems: factorization problem and discrete log problem, where thousands (say 2048) bits long key provides roughly 80 bits security level. \(\mathsf {P}_\mathtt{Fact}(p, q) = p \times q\) where both p and q are primes with equal bit-length. \(\mathsf {P}_\mathtt{Log} (x) = g^x \mod p\) where both g and p are public constants, p is a prime and g is a generator modulo p. Will the steal-entropy of these algorithm be closer to their key size (i.e. thousands) or security level (i.e. 80)? We leave it as an open problem.
4.3 Strong Steal-Entropy in Input
Informally, after stealing \(\ell \) bits arbitrary message, the adversary should be unable to output \(\ell + \varDelta \) bits information about the secret value, and there will be no leakage amplification.
Definition 3
(Strong Steal-Entropy of an Algorithm in Input). Let \(\mathsf {P}: \{ 0, 1 \}^{n} \rightarrow \{ 0,1 \}^{m}\) be a deterministicFootnote 11 single-input algorithm. Let \(\epsilon \in [0, \frac{1}{4})\). Let \(\mathcal {A}\) be a t-adversary associated with a pair of algorithms \( ({{\mathsf {S}}},\ {{\mathsf {R}}})\), such that
-
both the steal (or stealage) algorithm \({{\mathsf {S}}}\) and the recovery algorithm \({{\mathsf {R}}}\) are probabilistic algorithms within time t, and
-
for any non-negative integer \(\ell \), the steal algorithm
$$ {{\mathsf {S}}}^{\mathcal {O}(\mathsf {P}(x))}(\ell ) \in \{ 0,1 \}^{\le \ell } \setminus \{ \texttt {EmptyString} \} $$with oracle access to \(\mathsf {P}\), is allowed to observe all internal states during computation process of algorithm \(\mathsf {P}\) upon an input x, and outputs at most \(\ell \) bits non-empty steal-message, and
-
the recovery algorithm \({{\mathsf {R}}}\) takes 2 inputs: (1) the steal-message generated by \({{\mathsf {S}}}(\ell )\), and (2) the value \(\mathsf {P}(x)\), and outputs two values: (1) \(\bar{x} \in \{ 0,1 \}^{n}\), which is a guess of x, and (2) a subset of indices \(\mathbf {I}_x \subset [1, n]\).
We introduce the following definitions.
-
For any adversary \(\mathcal {A}\) with steal algorithm \({\mathsf {S}}\) and recovery algorithm \({\mathsf {R}}\), let us define the set \(\mathbf {G}_\mathtt{msg}\) of good steal-message as below
 (7)
(7)where the probability is taken over the random coins of \({\mathsf {R}}\).
-
Similarly, let us define the set \(\mathbf {G}_{x}\) of good input x as below
 (8)
(8)where the probability is taken over the random coins of \({\mathsf {S}}\).
-
We say the supremum of Strong Steal-Entropy in Input of algorithm \(\mathsf {P}\) is at most \(\xi \), denoted as \(\sup {{\mathbb {S}}}_{\epsilon , t}^{\mathtt{sin}}(\mathsf {P}) \le \xi \), if for some t-adversary \( \mathcal {A}=({{\mathsf {S}}}, {{\mathsf {R}}})\),
 (9)
(9)where function \(\varsigma (\cdot , \cdot )\) is defined as belowFootnote 12
 (10)
(10) -
Let \( \epsilon \ge \lambda ^{-c}\) where c could be any positive integer. We say the infimum of Strong Steal-Entropy in Input of algorithm \(\mathsf {P}\) is at least \(\xi \), denoted as \(\inf {{\mathbb {S}}}_{\epsilon , t}^{\mathtt{sin}}(\mathsf {P}) \ge \xi \), if for any t-adversary \( \mathcal {A}=({{\mathsf {S}}}, {{\mathsf {R}}})\), for any \(\ell \) with \(\varsigma (\ell , \epsilon )=\ell +1< \xi \),
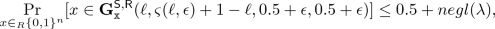 (11)
(11)where \(\lambda \) is the security parameter, and \(negl(\cdot )\) denotes some negligible function.
-
We say \({{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_0) \ge {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_1) \) (or equivalently \( {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_1) \le {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_0) \)), if the following two equations hold
$$\begin{aligned} \inf {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_0) \ge \inf {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_1); \sup {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_0) \ge \sup {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_1). \end{aligned}$$(12) -
We say \({{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_0) \gg {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_1) \)(or equivalently, \( {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_1) \ll {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_0) \)), if the following equation holds
$$\begin{aligned} \inf {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_0) \ge \sup {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}_1). \end{aligned}$$(13)
Lemma 1
(Amplification). If there exists some t-adversary \(\mathcal {A}_0=({\mathsf {S}}_0, {\mathsf {R}}_0)\), such that for any positive integer c, and for any \(\epsilon \ge \lambda ^{-c}\), we have

then there exists some \(t \cdot \varTheta (1/\epsilon )\)-adversary \(\mathcal {A}_1=({\mathsf {S}}_1, {\mathsf {R}}_1)\), such that

where \(\lambda \) is the security parameter and \(negl(\cdot )\) denotes some negligible function. (The proof is in our full version [28])
Definition 4
(Strong Steal-Entropy Rate in Input). Let \(\mathsf {P}: \{ 0, 1 \}^{n} \rightarrow \{ 0,1 \}^{m}\) be a deterministic single-input algorithm. We define the infimum and supremum of steal-entropy rate of algorithm \(\mathsf {P}\) as

(Note that this is a counterpart notion of “entropy rate” or “leakage rate”.)
Theorem 2
(Separation between Steal-Entropy and Strong Steal-Entropy). There exists a constant \(c>0\), such that for any positive integer N, we can construct an algorithm \(\mathsf {P}\), such that \(\sup {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\mathsf {P}) \le c\) and \(\inf {{\mathbb {S}}}_{\epsilon , t}^\mathtt{in}(\mathsf {P}) \ge N\). (Proof is in our full version [28])
5 Our Proposed Encryption (or Encoding) Scheme
We will describe our proposed encryption scheme in two steps following a modular design.
5.1 Our Steal-Resilient Encryption (or Encoding) Scheme
Definition 5
(Steal-Resilient Encryption/Encoding). Let \(\varPhi = (\mathsf {KeyGen},\)\( \mathsf {Encrypt}, \mathsf {Decrypt})\) be a length-preserving encryption scheme. Let algorithm \(\textsc {Suffix}_{\varPhi }\) be defined as below
Let n denote the length of plaintext. We say \(\varPhi \) is a \(\delta (n)\)-steal-resilient encryption scheme with split-factor \(\tau \), if the algorithm \(\textsc {Suffix}_{\varPhi }\) has infimum of strong steal-entropy rate \(\mu ^{\bot } = \frac{ \inf {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\textsc {Suffix}_{\varPhi }) }{n} \ge \delta (n)\), where \(\delta (n) \in [0, 1]\) with 1 meaning the best and 0 meaning the worst, \(t=O(poly(\lambda ))\), and \(\epsilon \ge \lambda ^{-c}\) for some positive integer c.
We remark that, under our definition, most existing encryption schemes (including any existing block cipher under any existing mode of operation, and All-or-Nothing Transform by Rivest [25], and Leakage resilient encryptionFootnote 13 [1, 2, 14, 17, 23, 27, 31]) are poorly \(\delta (n)\)-steal resilient encryption with \(\delta (n)=1/\varTheta (n)\) approaching to zero when n approaches to infinity.
We found that the linear transformation with Vandermonde matrix is a good steal-resilient encryption scheme. Let \(\rho \) be some positive integer (e.g. 8 or 16 or 32) and \(GF(2^{\rho })\) be a finite field with order \(2^{\rho }\).
We construct an encryption scheme \(\varPhi _0 = (\mathsf {KeyGen}, \mathsf {Encrypt}, \mathsf {Decrypt})\) as below.
\(\varPhi _0.\mathsf {KeyGen}(1^{\lambda }) \rightarrow \mathbf {M}\)
-
1.
Randomly choose a \(\zeta \cdot (1+\tau )\) by \(\zeta \cdot (1+\tau )\) Vandermonde matrixFootnote 14, and denote its transpose matrix as \(\mathbf {M} = \left( M_{i,j} \right) _{i,j \in [1, \zeta \cdot (1+\tau )]}\), where \(M_{i,j} = \alpha _j^{i} \in GF(2^{\rho }) \setminus \{ 0\}\). The inverse of matrix \(\mathbf {M}\) exists and is denoted as \(\mathbf {M}^{-1}\).
-
2.
Output \(\mathbf {M}\).
\(\varPhi _0.\mathsf {Encrypt}(\mathbf {M}; \varvec{\varvec{x}})\), where \(\mathbf {M}\) is a \(\zeta \cdot (1+\tau )\) by \(\zeta \cdot (1+\tau )\) matrix and \(\varvec{\varvec{x}} \in GF(2^{\rho })^{\zeta \cdot (1+\tau )}\) is a row vector of dimension \(\zeta \cdot (1+\tau )\) (equivalently, 1 by \(\zeta \cdot (1+\tau )\) matrix)
-
1.
Compute product \(\varvec{\varvec{y}} := \varvec{\varvec{x}} \times \mathbf {M}^{-1}\) of two matrix \(\varvec{\varvec{x}}\) and \(\mathbf {M}^{-1}\).
-
2.
Treat \(\varvec{\varvec{y}}\) as a bit string with length \((1+\tau )\rho \zeta \) bits, which is the concatenation of \(\zeta (1+\tau )\) number of ordered \(\rho \)-bits finite field elements.
-
3.
Let \(\varvec{\varvec{y}}_0\) be the prefix of \(\varvec{\varvec{y}}\) with length equal to \(\rho \zeta \) bits.
-
4.
Let \(\varvec{\varvec{y}}_1\) be the suffix of \(\varvec{\varvec{y}}\) with length equal to \(\tau \rho \zeta \) bits.
-
5.
Output \((\varvec{\varvec{y}}_{0}, \varvec{\varvec{y}}_{1})\).
\(\varPhi _0.\mathsf {Decrypt}(\mathbf {M}; \varvec{\varvec{y}}_{0}, \varvec{\varvec{y}}_{1})\)
-
1.
Let \(\varvec{\varvec{y}}\) be the concatenation of \(\varvec{\varvec{y}}_0\) and \(\varvec{\varvec{y}}_1\).
-
2.
Parse bit-string \(\varvec{\varvec{y}}\) as a row vector of dimension \(\zeta (1+\tau )\) where each vector element is from \(GF(2^{\rho })\).
-
3.
Compute matrix product \(\varvec{\varvec{x}} := \varvec{\varvec{y}} \times \mathbf {M}\).
-
4.
Output \(\varvec{\varvec{x}}\).
We remark that, any linear transformation with an invertible matrix could constitute an information dispersal algorithm [24], but is unlikely a steal-resilient encryption.
Our experiments in a Macbook Pro Laptop with Intel i5 CPU (purchased in 2014) show that the encryption or decryption can be done in 0.037 s (about 21 megabytes per second) with a single CPU core when dimension of \(\mathbf {M}\) is 12800 and \(\rho =16, \tau =31\); and in 0.149 s when dimension is 25600 and \(\rho =16, \tau =63\).
Theorem 3
Let \(\varvec{\varvec{x}} := \varvec{\varvec{y}} \times \mathbf {M}\) be as stated in the above scheme. Then \(\varvec{\varvec{x}}\) follows \((\zeta , \rho )\)-Blockwise-Uniform distribution, as defined in Definition 1 on page 9. More precisely, parse \(\varvec{\varvec{x}}\) as a sequence of elements \((x_1, x_2, \cdots , x_i, \cdots , x_{\zeta (1+\tau )})\) with each element \(x_i \in GF(2^{\rho })\). If the last \(\tau \cdot \zeta \) elements of \(\varvec{\varvec{y}}\) is given and fixed, and the first \(\zeta \) elements of \(\varvec{\varvec{y}}\) uniformly distributes over \(\{ 0,1 \}^{\rho \zeta }\), then any tuple of \(\zeta \) elements \((\cdots , x_{i_j}, \cdots )_{j \in [1, \zeta ]}\), with distinct indices \(i_j\)’s, will have exactly \(\rho \cdot \zeta \) bits Shannon-Entropy (i.e. the Shannon-Entropy rate is 1). Proof is in full version [28].
Corollary 4
The proposed scheme \(\varPhi _0\) is a \(\delta (n)\)-steal-resilient encryption, with \(\delta (n) = \frac{1}{\rho (\tau +1)}\) independent on plaintext length \(n= \rho \zeta (1+\tau )\), and \( \inf {{\mathbb {S}}}_{\epsilon , t}^\mathtt{sin}(\textsc {Suffix}_{\varPhi _0}) \ge \zeta \). We remark that both \(\rho \) and \(\tau \) are system parameters independent on plaintext length n. (Proof is in our full version [28])
We observe that, in the proof of Theorem 3, we only require the first \(\zeta \) rows of matrix \(\mathbf {M}\) satisfy the special Vandermonde matrix property. Therefore, we could simply tweak the rest rows of matrix \(\mathbf {M}\), in order to speed up the decryption performance.
Corollary 5
In algorithm \(\varPhi _0.\mathsf {KeyGen}\), change the last \(\tau \zeta \) rows of matrix \(\mathbf {M}\) to a sparse matrix, such that \(\mathbf {M}\) is still invertible. Then the resulting variant version of \(\varPhi _0\) is still \(\delta (n)\)-steal-resilient encryption, with \(\delta (n) = \frac{1}{\rho (\tau +1)}\), where \(n = \rho \zeta (1+\tau )\).
The above Corollary 5 actually separates our notion from secret-sharing scheme: After the tweak in the above corollary, the resulting scheme is no longer a secret sharing scheme.
5.2 Combine Steal-Resilient Encryption and Semantic Secure Encryption
We wish to combine both of the advantage of Steal-Resilient Encryption in leakage setting, and the advantage of semantic secure encryption in standard adaptive chosen message/plaintext attack setting (CCA2/CPA2).
Let \(\varPhi _{0}\) be the steal-resilient encryption scheme defined above. Let \(\varPhi _{1}\) be a given semantic-secure encryption scheme (precisely, CTR mode of a semantic secure block cipher). Eventually, our encryption scheme \(\varPhi _{2}\) is defined as below
-
\(\varPhi _{2}.\mathsf {KeyGen}(1^{\lambda }) \leftarrow (k, k_0, k_1)\):
-
1.
Compute key \(\mathbf {M} \leftarrow \varPhi _{0}.\mathsf {KeyGen}(1^{\lambda })\).
-
2.
Compute key \(k \leftarrow \varPhi _{1}.\mathsf {KeyGen}(1^{\lambda })\).
-
3.
Output \((k, \mathbf {M})\).
-
1.
-

-
1.
Encrypt plaintext \(\mathtt {Msg}\) using semantic secure encryption to obtain ciphertext \(\mathtt{{Ctx}} \leftarrow \varPhi _{1}.\mathsf {Encrypt}(k; \mathtt {Msg})\).
-
2.
Split the ciphertext \(\mathtt{{Ctx}}\) into two shares using steal-resilient encryption
 .
. -
3.
Output \((C_0, C_1)\).
-
1.
-
\(\varPhi _{2}.\mathsf {Dec}(k, \mathbf {M}; C_0, C_1)\)
-
1.
Merge the two shares \(C_0\) and \(C_1\) as ciphertext
 .
. -
2.
Decrypt \(\mathtt {Ctx}\) as \(\mathtt{Msg} \leftarrow \varPhi _{1}.\mathsf {Decrypt}(k; \mathtt {Ctx})\).
-
3.
Output \(\mathtt {Msg}\).
-
1.
We remark that, in our proposed scheme, for large input size, \(\varPhi _1\) can run in CTR mode and \(\varPhi _0\) can run over every \(\rho \zeta (1+\tau )\)-bit segment in ciphertext of \(\varPhi _1\) independently.
Theorem 6
Let \(\varPhi _2\) be the proposed encryption scheme by combining a steal-resilient encryption \(\varPhi _0\) and a semantic secure encryption \(\varPhi _1\). Then \(\varPhi _2\) is semantic-secure in standard model, and is \(\delta (n)\)-steal-resilient encryption with split-factor \(\tau \) in our leakage-model, where \(1/\delta (n) = \rho (\tau +1) + O(1)\). (Proof is given in our full version [28]).
6 Conclusion
In this work, we proposed a new and strong leakage setting, a novel notion of computational entropy, and a construction to achieve higher security against strong leakage. We separated our new notion from several relevant existing concepts, including Yao-Entropy, Hill-Entropy, All-or-Nothing Transform, Exposure Resilient Function. Unlike most of previous leakage resilient cryptography works which focused on defeating side-channel attacks, we opened a new direction to study how to defend against backdoor (or Trojan horse) and covert channel attacks.
Notes
- 1.
- 2.
- 3.
The encryption scheme is length-preserving, and the size of ciphertext is equal to the size of plaintext.
- 4.
Note: (1) Many cloud storage servers provide a certain amount (e.g. 15GB) of free cloud storage for individual users; (2) the cost of offline local storage should include not only hardware purchase cost but also hardware maintenance and storage cost (i.e. keep the harddisk drive in a proper physical environment for a long time).
- 5.
Actually, the motivation of this work is to provide an extremely secure (informally, close to physically isolated network) communication method in this “virtually isolated network” [29]. Here we choose strong leakage resilience against potential backdoor as our formal definition of “extremely secure”.
- 6.
Usually, it is assumed that the adversary has access to the ciphertext.
- 7.
- 8.
- 9.
Shannon-Entropy is information-theoretical. Both Yao-Entropy and Hill-Entropy are computational variants.
- 10.
When all random coins are treated as a part of input, any probabilistic algorithm will become deterministic.
- 11.
When all random coins are treated as a part of input, any probabilistic algorithm will become deterministic.
- 12.
The reason behind the definition of \(\varsigma (\ell , \sigma )\) (i.e. Eq. 10) is explained with details in our full version of this paper. Informally speaking, some steal algorithm \({{\mathsf {S}}}(\ell )\) is able to convey almost \(\ell +1\) bits message to \(\mathsf {R}\) algorithm, since \(| \{ 0, 1 \}^{\le \ell } | \approx |\{ 0,1 \}^{\ell +1}|\). When the error bound \(\epsilon \ge 2^{-(\ell -1)}\), we do not care the difference between such “almost” \(\ell +1\) bits message and actual \(\ell +1\) bits message.
- 13.
We remark that some of these cited leakage resilient cryptography works actually propose leakage resilient pseudorandom generator/functions, instead of an encryption scheme. These pseudorandom generator/functions can be converted into encryption scheme using classical methods. These resulting encryption schemes will be a poor steal-resilient encryption.
- 14.
The matrix row/column index starts with either zero or one, makes no essential difference to the property of Vandermonde matrix.
References
Abdalla, M., Belaïd, S., Fouque, P.A.: Leakage-resilient symmetric encryption via re-keying. In: Proceedings of the 15th International Conference on Cryptographic Hardware and Embedded Systems, CHES 2013, pp. 471–488 (2013)
Alwen, J., Dodis, Y., Wichs, D.: Leakage-resilient public-key cryptography in the bounded-retrieval model. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 36–54. Springer, Heidelberg (2009). https://doi.org/10.1007/978-3-642-03356-8_3
Alwen, J., Dodis, Y., Wichs, D.: Survey: leakage resilience and the bounded retrieval model. In: Proceedings of the 4th International Conference on Information Theoretic Security, ICITS 2009, pp. 1–18 (2010)
Kolmogorov, A.N.: On tables of random numbers. Theor. Comput. Sci. 207, 387–395 (1998)
Barak, B., et al.: On the (im)possibility of obfuscating programs. J. ACM 59(2), 6:1–6:48 (2012)
Barwell, G., Martin, D.P., Oswald, E., Stam, M.: Authenticated encryption in the face of protocol and side channel leakage. Cryptology ePrint Archive, Report 2017/068 (2017). https://eprint.iacr.org/2017/068
Barwell, G., Martin, D.P., Oswald, E., Stam, M.: Authenticated encryption in the face of protocol and side channel leakage. In: Takagi, T., Peyrin, T. (eds.) ASIACRYPT 2017. LNCS, vol. 10624, pp. 693–723. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-70694-8_24
Ben Othman, J., Mokdad, L.: Enhancing data security in ad hoc networks based on multipath routing. J. Parallel Distrib. Comput. 70, 309–316 (2010)
Bronchain, O., Dassy, L., Faust, S., Standaert, F.X.: Implementing Trojan-resilient hardware from (mostly) untrusted components designed by colluding manufacturers. In: Proceedings of the 2018 Workshop on Attacks and Solutions in Hardware Security, ASHES 2018, pp. 1–10. ACM, New York (2018). https://doi.org/10.1145/3266444.3266447
Canetti, R., Dodis, Y., Halevi, S., Kushilevitz, E., Sahai, A.: Exposure-resilient functions and all-or-nothing transforms. In: Preneel, B. (ed.) EUROCRYPT 2000. LNCS, vol. 1807, pp. 453–469. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-45539-6_33
Daemen, J., Rijmen, V.: The Design of Rijndael: AES - The Advanced Encryption Standard (2002)
Apon, D., Huang, Y., Katz, J., Malozemoff, A.J.: Implementing cryptographic program obfuscation. Cryptology ePrint Archive, Report 2014/779 (2014). https://eprint.iacr.org/2014/779
Di Crescenzo, G., Lipton, R., Walfish, S.: Perfectly secure password protocols in the bounded retrieval model. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 225–244. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_12
Dodis, Y., Haralambiev, K., López-Alt, A., Wichs, D.: Efficient public-key cryptography in the presence of key leakage. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 613–631. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-17373-8_35
Dziembowski, S.: Intrusion-resilience via the bounded-storage model. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 207–224. Springer, Heidelberg (2006). https://doi.org/10.1007/11681878_11
Dziembowski, S., Faust, S., Standaert, F.X.: Private circuits III: hardware Trojan-resilience via testing amplification. In: Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security, CCS 2016, pp. 142–153. ACM, New York (2016). https://doi.org/10.1145/2976749.2978419
Dziembowski, S., Pietrzak, K.: Leakage-resilient cryptography. In: Proceedings of the 2008 49th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2008, pp. 293–302, IEEE Computer Society, Washington, DC, USA (2008). https://doi.org/10.1109/FOCS.2008.56
Goldwasser, S., Kalai, Y.T.: On the impossibility of obfuscation with auxiliary input. In: Proceedings of the 46th Annual IEEE Symposium on Foundations of Computer Science, FOCS 2005, pp. 553–562 (2005)
HÅsstad, J., Impagliazzo, R., Levin, L.A., Luby, M.: A pseudorandom generator from any one-way function. SIAM J. Comput. 28(4), 1364–1396 (1999)
Krawczyk, H.: Secret sharing made short. In: Stinson, D.R. (ed.) CRYPTO 1993. LNCS, vol. 773, pp. 136–146. Springer, Heidelberg (1994). https://doi.org/10.1007/3-540-48329-2_12
McEliece, R.J., Sarwate, D.V.: On sharing secrets and Reed-Solomon codes. Commun. ACM 24(9), 583–584 (1981)
Micali, S., Reyzin, L.: Physically observable cryptography. In: Naor, M. (ed.) TCC 2004. LNCS, vol. 2951, pp. 278–296. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-24638-1_16
Pereira, O., Standaert, F.X., Vivek, S.: Leakage-resilient authentication and encryption from symmetric cryptographic primitives. In: Proceedings of the 22nd ACM SIGSAC Conference on Computer and Communications Security, CCS 2015, pp. 96–108 (2015)
Rabin, M.O.: Efficient dispersal of information for security, load balancing, and fault tolerance. J. ACM 36(2), 335–348 (1989). https://doi.org/10.1145/62044.62050
Rivest, R.L.: All-or-nothing encryption and the package transform. In: Proceedings of the 4th International Workshop on Fast Software Encryption, FSE 1997, pp. 210–218 (1997)
Shamir, A.: How to share a secret. Commun. ACM 22(11), 612–613 (1979)
Standaert, F.-X., Pereira, O., Yu, Y.: Leakage-resilient symmetric cryptography under empirically verifiable assumptions. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 335–352. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40041-4_19
Xu, J., Zhou, J.: Strong leakage resilient encryption by hiding partial ciphertext. Cryptology ePrint Archive, Report 2018/846 (2018). https://eprint.iacr.org/2018/846
Xu, J., Zhou, J.: Virtually isolated network: a hybrid network to achieve high level security. In: Data and Applications Security and Privacy XXXII, DBSec 2018, pp. 299–311 (2018)
Yao, A.C.C.: Theory and applications of trapdoor functions. In: Proceedings of 23rd Annual Symposium on Foundations of Computer Science, EUROCRYPT 2007, pp. 80–91 (1982)
Yu, Y., Standaert, F.X., Pereira, O., Yung, M.: Practical leakage-resilient pseudorandom generators. In: Proceedings of the 17th ACM Conference on Computer and Communications Security, CCS 2010, pp. 141–151. ACM, New York (2010). https://doi.org/10.1145/1866307.1866324
Acknowledgment
The first author is supported by the National Research Foundation, Prime Minister’s Office, Singapore under its Corporate Laboratory@University Scheme, National University of Singapore, and Singapore Telecommunications Ltd. The second author is supported by the National Research Foundation (NRF), Prime Minister’s Office, Singapore, under its National Cybersecurity R&D Programme (Award No. NRF2014NCR-NCR001-31) and administered by the National Cybersecurity R&D Directorate.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Xu, J., Zhou, J. (2019). Strong Leakage Resilient Encryption by Hiding Partial Ciphertext. In: Zhou, J., et al. Applied Cryptography and Network Security Workshops. ACNS 2019. Lecture Notes in Computer Science(), vol 11605. Springer, Cham. https://doi.org/10.1007/978-3-030-29729-9_10
Download citation
DOI: https://doi.org/10.1007/978-3-030-29729-9_10
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-29728-2
Online ISBN: 978-3-030-29729-9
eBook Packages: Computer ScienceComputer Science (R0)






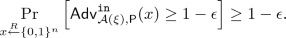




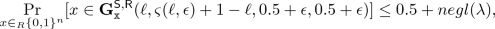

 .
. .
.