Abstract
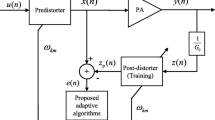
This paper proposes the adaptive indirect learning architecture (ILA) based digital predistortion (DPD) technique using a recursive prediction error minimization (RPEM) algorithm for linearizing radio frequency (RF) power amplifiers (PAs). The RPEM algorithm allows the forgetting factor to vary with time, which makes the predistorter (PD) parameter estimates more consistent and accurate in steady state, and hence reduces mean square errors. The proposed DPD technique is evaluated with respect to the error vector magnitude (EVM) and the adjacent channel power ratio (ACPR). The simulated PA Wiener model is used to validate the efficiency of the proposed algorithms. The simulation results have confirmed the improvement of the proposed adaptive RPEM ILA based DPD in terms of EVM and ACPR.
This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 102.02-2016.12.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
References
Vo, H.M.: Implementing energy saving techniques for sensor nodes in IoT applications. EAI Endorsed Trans. Ind. Netw. Intell. Syst. 5(17), 1–7 (2018)
Ghannouchi, F.M., Hammi, O.: Behavioral modeling and predistortion. IEEE Microwave Mag. 10(7), 52–64 (2009)
Chani-Cahuana, J., Landin, P.N., Fager, C., Eriksson, T.: Iterative learning control for RF power amplifier linearization. IEEE Trans. Microw. Theory Tech. 64(9), 2778–2789 (2016)
Guan, L., Zhu, A.: Green communications: digital predistortion for wideband RF power amplifiers. IEEE Microwave Mag. 15(7), 84–99 (2014)
Ding, L., et al.: A robust digital baseband predistorter constructed using memory polynomials. IEEE Trans. Commun. 52(1), 159–165 (2004)
Guo, Y., Yu, C., Zhu, A.: Power adaptive digital predistortion for wideband RF power amplifiers with dynamic power transmission. IEEE Trans. Microw. Theory Tech. 63(11), 3595–3607 (2015)
Schoukens, M., Hammenecker, J., Cooman, A.: Obtaining the preinverse of a power amplifier using iterative learning control. IEEE Trans. Microw. Theory Tech. 65(11), 4266–4273 (2017)
Zhou, D., DeBrunner, V.E.: Novel adaptive nonlinear predistorters based on the direct learning algorithm. IEEE Trans. Signal Process. 55(1), 120–133 (2007)
Choi, S., Jeong, E.R., Lee, Y.H.: Adaptive predistortion with direct learning based on piecewise linear approximation of amplifier nonlinearity. IEEE Sel. Topics Signal Process. 3(3), 397–404 (2009)
Suryasarman, P.M., Springer, A.: A comparative analysis of adaptive digital predistortion algorithms for multiple antenna transmitters. IEEE Trans. Circuits Syst. I 62(5), 1412–1420 (2015)
Eun, C., Powers, E.J.: A new Volterra predistorter based on the indirect learning architecture. IEEE Trans. Signal Process. 45(1), 223–227 (1997)
Morgan, D.R., Ma, Z., Ding, L.: Reducing measurement noise effects in digital predistortion of RF power amplifiers, vol. 4, pp. 2436–2439, May 2003
Paaso, H., Mammela, A.: Comparison of direct learning and indirect learning predistortion architectures. In: Proceedings of IEEE International Symposium on Wireless Communication Systems, pp. 309–313, October 2008
Hussein, M.A., Bohara, V.A., Venard, O.: On the system level convergence of ILA and DLA for digital predistortion. In: Proceedings of 2012 International Symposium on Wireless Communication Systems (ISWCS), pp. 870–874, August 2012
Mohr, B., Li, W., Heinen, S.: Analysis of digital predistortion architectures for direct digital-to-RF transmitter systems. In: Proceedings of 2012 IEEE 55th International Midwest Symposium on Circuits and Systems (MWSCAS), pp. 650–653, August 2012
Söderström, T., Stoica, P. (eds.): System Identification. Prentice-Hall Inc., Upper Saddle River (1988)
Abdelrahman, A.E., Hammi, O., Kwan, A.K., Zerguine, A., Ghannouchi, F.M.: A novel weighted memory polynomial for behavioral modeling and digital predistortion of nonlinear wireless transmitters. IEEE Trans. Ind. Electron. 63(3), 1745–1753 (2016)
Mkadem, F.: Behavioral modeling and digital predistortion of wide- and multi-band transmitter systems. Ph.D. dissertation (2014)
Feng, X., Wang, Y., Feuvrie, B., Descamps, A.-S., Ding, Y., Yu, Z.: Analysis on LUT based digital predistortion using direct learning architecture for linearizing power amplifiers. EURASIP Wirel. Commun. Netw. 2016(1), 132 (2016)
Kwon, J., Eun, C.: Digital feedforward compensation scheme for the non-linear power amplifier with memory. IJISTA 9, 326–334 (2010)
Eun, C., Powers, E.J.: A predistorter design for a memory-less nonlinearity preceded by a dynamic linear system. In: Proceedings of GLOBECOM 1995, vol. 1, pp. 152–156, November 1995
Saleh, A.A.M.: Frequency-independent and frequency-dependent nonlinear models of TWT amplifiers. IEEE Trans. Commun. COM–29(11), 1715–1720 (1981)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 ICST Institute for Computer Sciences, Social Informatics and Telecommunications Engineering
About this paper
Cite this paper
Le Duc, H., Nguyen, M.H., Hoang, VP., Nguyen, H.M., Nguyen, D.M. (2019). Linearizing RF Power Amplifiers Using Adaptive RPEM Algorithm. In: Duong, T., Vo, NS., Nguyen, L., Vien, QT., Nguyen, VD. (eds) Industrial Networks and Intelligent Systems. INISCOM 2019. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, vol 293. Springer, Cham. https://doi.org/10.1007/978-3-030-30149-1_18
Download citation
DOI: https://doi.org/10.1007/978-3-030-30149-1_18
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-30148-4
Online ISBN: 978-3-030-30149-1
eBook Packages: Computer ScienceComputer Science (R0)