Keywords

1 Introduction

The total number of digital images acquired, stored or shared all over the world is unimaginable and constantly growing due to the spread of social networks. Simultaneously, the importance of proving the authenticity of digital data is increasing. If an image is involved in a forensic investigation it is mandatory to demonstrate the originality or integrity for the image itself. The difference between the integrity and the authenticity of an image is the following: the process to demonstrate the integrity of an image is related to the certainty that the image was acquired, stored in an image file and never edited again; if the image was successively transformed but its meaning didn’t change we can define the image authentic although it lost the integrity. Most of the times the image is acquired and stored by devices such as digital camera or smartphone directly in JPEG compressed format. If an already-acquired image is opened, manipulated in some way and then saved into another image file, this last one is different from the original thus it lost its integrity. Consequently, according to the last definition all the images on social networks can be considered without integrity but nothing can be said about authenticity. Thus the Double Compression Detection in an image is the first step for any digital forensics image analysis: if no double compression is detected, the integrity of the image has not been lost, it is authentic and no further analyses are needed, otherwise additional analysis like tampering or copy-move-forge detection should be carried out [3]. Given that the alteration of an image involves a multiple JPEG compression process, it is possible to detect some traces of this on the image itself. These traces are strictly related to the JPEG algorithm and the compression parameters used each time the image was saved and stored in a JPEG image file. State-of-the-art already demonstrated that the most important piece of information of a digital image is hidden in the DCT domain. This piece of information has to be discovered and correctly represented in a mathematical form. Thus it can be employed for many automated image processing tasks [2, 4, 5, 11, 26] like object recognition, scene recognition or image forensics. In this paper, in order to find a new technique for the Double Compression Detection problem, the DCT domain of single and double compressed JPEG images was investigated and interesting insights were detected in the first digits statistics of elements in 1-D DCT transformed \(8\times 8\) blocks of an image. This is the main contribution of this paper. The discovered insights are very interesting in terms of their simplicity and might open new research paths. Their potential was also demonstrated by exploiting them as features for a simple Machine Learning classifier for double compressed image detection and by comparison with state-of-the-art. The remainder of this paper is organized as follows. In Sect. 2 a brief background of JPEG compression algorithm and properties useful to better understand this paper will be presented. Then, in Sect. 3 the state-of-the-art of double compression detection methods will be discussed. Section 4 will describe the employed datasets on which the investigation in the DCT domain described in Sect. 5 was carried out. Section 6 demonstrates the usability of the discovered insights in an automated classifier and Sect. 7 shows and discusses the achieved results with comparisons with state-of-the-art methods. Finally Sect. 8 concludes this paper with some ideas for further works.

2 JPEG Compression and Double Compression

The JPEG compression is probably the most well-known method for image’s compression. In brief, starting from a RAW color image, the main steps of the JPEG algorithm are the following: at first the luminance component is separated from the chrominance one converting the input image from the RGB to YC bC r. After that the image is partitioned into \(8\times 8\) non overlapping blocks and the corresponding values are converted from unsigned integer, in the range [0, 255], to signed values belonging to the range \([-128,127]\). At this point a 2-D DCT transform is applied to each block, followed by a Quantization, using for each DCT coefficient of the \(8\times 8\) non-overlapping block a corresponding integer value defined in a Quantization Table. The elements in the Quantization Table are related to the so called Quality Factor (QF) which defines the level of compression and reduction of information obtainable by JPEG. The quantized coefficients obtained are then rounded and the results of the ratio between the original DCT coefficients and the corresponding quantized ones, are then transformed into a data stream furtherly encoded by entropic compression. The entire process is lossy and this lossy behaviour leaves traces on images that can be exploited to predict if an image has gone through the JPEG algorithm. It is easy to note that the principal step in the JPEG algorithm which mainly reduces the information (and the size) in an image is the quantization step. Thus most of papers talk about Double Quantization Detection (DQD). The quantization step is driven in its outcome by the QF. Then for each compression a \(QF-n\) is defined where n is how many times the image have gone through a JPEG compression process.

3 Related Works

Many DQD techniques have been proposed in literature during the last years. At first, Fan and De Queiroz [9, 10], described an approach able to discriminate between images not compressed and JPEG compressed ones, independently from the number of compressions performed. They exploited the banal insight that if an image has never been previously JPEG-compressed, then the pixel differences across \(8\times 8\) block boundaries should not be noticeable.

The first attempt on detecting single vs. double JPEG compression was presented in [12] where the authors demonstrated that the distribution probability of the first digits law of the DCT coefficients in original JPEG images (single-compressed) follows a Benford-like logarithmic law ([14]). In [17] the authors furtherly analyzed the first digit distribution of each sub-band of DCT coefficients independently, while [15] extended the Benford-like law including the zero in the first digit distribution. Machine Learning classification technique were introduced by the works of [6] (inspired by [20]), and [8], which is itself a refinement of [7]. In [32] the authors built probability maps upon JPEG DCT coefficients, exploiting PCA for dimensional reduction and SVMs for classification. Pasquini et al. [22], proposed a binary decision test, based on the Benford-Fourier theory and improved it in [23] or even more [24] to face also multi (up to three) JPEG compressions and finally refining it in [25] with the introduction of features from images analysed in the spatial domain. On the other hand in [31] the authors created a new feature called factor histogram describing the distribution of the factors related to quantized DCT coefficients.

With the widespread of machine learning techniques and specifically Convolutional Neural Networks (CNN), new methods have been proposed for the DQD problem  [1, 18, 21, 28, 29]. CNNs have demonstrated to be incredibly powerful in finding invisible correlation in data, specifically on images, but they are also very intensive in terms of computational costs, prone to overfitting and strictly related to the dataset on which they trained. Moreover, most of the predicted outcomes are not explainable and unpredictable making the use of CNNs uneffective in forensics. However, Li et al. [19] and Wang et al. [30] proposed new DQD techniques able to outperform even CNNs. They are based on the statistics between adjacent DCT coefficients in \(8\times 8\) blocks of an image. In particular [19] rearranged the \(8\times 8\) blocks in \(1\times 64\) blocks thus extracting adjacent elements statistics as a feature vector for a SVM classifier, while [30] processed adjacent elements by means of a Markov Model, thus building a new feature vector for a SVM binary classifier.

4 Dataset

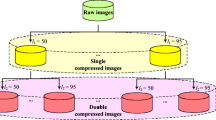
The aim of this paper is to investigate images in the DCT domain in order to find insights or a technique that works for the DQD task opening new research paths and outperforming the state-of-the-art. To this aim the analysis were perfomed on different datasets. The first one, is synthetic and constructed starting from the UCID dataset [27] employs standard-tables (with non standard tables ones only for same QF1-QF2), so it will be called UCID-derived. It is composed by 500 random images compressed twice into new JPEG images in order to cover many combination of QF1-QF2 as described below:

$$\begin{aligned} QF1_n n \in [100/95/90/......./50] \end{aligned}$$
(1)
$$\begin{aligned} QF2_m m \in [100/95/90/......./50] \end{aligned}$$
(2)

This process created 121 sets of 500 images for each couple of Quality Factors QF1-QF2 The second dataset is the dataset presented in Giudice et al. [13] which contains images downloaded from social networks and the corresponding original ones. This last dataset employs completely non-standard tables, and is useful to evaluate all considerations and techniques in the wild with image coming from everyday usage: indeed images downloadable from Social Networks are double (or multiple) compressed. Being in the wild the dataset presents many combinations of QF1-QF2 most of them are estimable but not known a priori.

Fig. 1.
figure 1

First Digit distribution on images. (a) shows the Benford’s law (blue) and the first digit distribution averaged on all 64 elements of 2-D DCT transformed \(8\times 8\) blocks. The green line shows the single compressed distribution while the red one the distribution obtained from double compressed images. The three curves are fully overlapped. Better separation is obtainable by computing the first digit statistics on only one element of the \(8\times 8\) block, as shown in (b) or by computing it after 1-D DCT transform (c). This last distributions while being easily and visibly separable differs from the Benford’s law. (Color figure online)

Full size image

5 Investigating the DCT Domain

An evaluation of those studies based on the first digit statistics w.r.t. the Benford’s Law ([12, 17] and [15]) was carried out on images, taken in the wild from social networks taken from the dataset presented in [13]. Figure 1a shows the normalized histogram of the First Digit statistics obtained for single and double compressed images w.r.t. the Benford’s Law in which all curves are perfectly overlapping. This demonstrates that all those approaches work only on specific conditions and are not effective in the wild. The main problem of [12, 17] and [15], is that they compute statistics from all the 63 numbers obtained after the 2-D DCT transformation, in each \(8\times 8\) block. In this way components related to many frequencies are “mixed” altogether averaging everything. Indeed, taking into account the first digit statistics of just one coefficient is also almost ineffective, as shown in Fig. 1b: the curves obtained on single and double compressed images are overlapping and also are both separating from the Benford’s law. The separation, of the two curves, can be obtained by evaluating a 1D-DCT transformation on the \(8\times 8\) blocks. In this way a directional DCT is computed (through the vertical or horizontal direction) and the first digit statistics for single and double compressed images become separable as shown in Fig. 1c. Having two separate histograms means that the distribution is a good feature to be exploited for the DQD problem. Figure 1c shows the statistics obtained on the best element w.r.t. the separation of the two curves: not all elements showed a good separation, thus a further analysis was carried out on \(8\times 8\) blocks transformed through both 1-D DCT (in both directions) and 2-D DCT. Figure 2 shows the heatmaps for the three analysis, for each of the 64 elements in a \(8\times 8\) block. Each element (i, j) in the three heatmaps is represented in terms of the obtained cosine distance between the first digit statistics between the single and the double compressed image obtained on (i, j). The distance value is averaged through all images on the social network images dataset [13]. In particular, Fig. 2a, as already stated for Fig. 1b, shows that 2D-DCT produce not very separable histograms (black color means low distance values), while Figs. 2b and 2c show that both directions of 1D-DCT achieve a very good separation. Specifically, the best separation in terms of distance values is obtained on elements in the bottom part of the \(8\times 8\) block for vertical 1-D DCT and in the right part of the \(8\times 8\) block in the horizontal 1-D DCT. The 1-D DCT transform in conjunction with the first digit statistics is able to produce a good histogram separation for single and double compressed images, but those curves as shown in Fig. 1c do not follow the Benford’s Law, thus a new law should be used to detect double compressed images. To this aim a novel classification technique was experimented and will be presented in the next section.

Fig. 2.
figure 2

Heatmap representation of cosine distance values between the first digit statistics obtained for single and double compressed image. The distance is computed for each element inside the \(8\times 8\) block. Black values means distance equal to zero. (a) shows the distance values obtained after 2-D DCT transform while values obtained after 1-D DCT trasform are shown in (b) w.r.t. vertical direction and (c) horizontal one.

Full size image

6 Validation Through Automated DQD Technique

The insights obtained through the investigation carried out and described in this paper suggested a simple computational approach, together with visible statistics that allow to detect double compressed images. In order to evaluate if this feature can be exploited to correctly detect double compressed images, a test on many samples has to be carried out. Thus, a classification technique was built in order to model the new law, that was demonstrated to be different from the Benford’s one, able to automatically detect double compressed images. The DQD law is modelled on top of all the explainable insights described in Sect. 5 and takes into account a feature vector that not only contains the statistics of all the first digits (including 0), but also the signs statistics (positive or negative) of the elements. Thus, a 13-dimensional feature vector was obtained for each of the 64 elements of the \(8\times 8\) blocks processed with the 1-D DCT transformation.

In a more formal representation, given a JPEG image I, it is possible to divide it into N non-overlapping \(8\times 8\) pixels blocks \(B_n\) with \(n \in {[0,N-1]}\), and with each \(B_n\) containing 64 elements \(B_n(i,j)\) with \(i,j \in [0,7]\). Given the first digit function definition as follows:

$$\begin{aligned} FirstDigit_d(x) = \bigg \{ \begin{array}{rl} 1 &{} \text {if}\,\, x\,\, \text {has a value with the first digit equal to}\,\, d \\ 0 &{} \text {otherwise} \\ \end{array} \end{aligned}$$
(3)

Starting from an element at position (i, j) in the \(8\times 8\) block it is possible to compute the first digit and signs statistics, for all \(n \in {[0,N-1]}\) as follows:

$$\begin{aligned} H_d(i,j) = \sum _n FirstDigit_d(B_n(i,j)) \end{aligned}$$
(4)

Thus the full 13-dimensions feature vector H(i, j) for image I with N \(8\times 8\) non-overlapping blocks and element at position (i, j) is defined as follows:

$$\begin{aligned} H(i,j) = {H_0(i,j),...,H_9(i,j),H_{pos}(i,j),H_{neg}(i,j), H_{null}(i, j)} \end{aligned}$$
(5)

where \(H_{pos}(i, j), H_{neg}(i, j)\) and \(H_{null}(i, j)\) are the number of elements at position (i, j) that are positive, negative or zero respectively. The selection of a proper classification method is out of the scope of this paper, given that it is only exploited for validation purposes. Many classification algorithms were experimented and best result were obtained with the Gradient Boosting technique. The Gradient Boosting (GBoost) technique was employed to train 64 different classifiers C(i, j) for each element in the \(8\times 8\) block. As expected, best results were obtained w.r.t. highest frequency components among the elements of the \(8\times 8\) block transformed through any of the two 1-D DCT transforms. This was expected as already visually-described by distance values of histogram curves shown in Fig. 2.

7 Experimental Results

The experimental phase was carried out by training and then testing the images from the two datasets described in Sect. 4. The UCID-derived image dataset were divided into two sets: training set and test set. The training set was used to train the 64 classifiers (one for each element of the \(8\times 8\) block) and the test set was employed to compute the accuracy measurements. The test was repeated by means of 5-fold Cross Validation and the results reported in this paper are the average accuracy measurements among all runs. In Table 1 the obtained accuracy measurements are shown and compared with the most recent state-of-the-art techniques for each couple of QF1-QF2. In almost all the different cases the proposed technique outperforms the current methods described in literature. Moreover, the proposed technique is able to detect double compression in images with \(QF1 = QF2\), as it was investigated by Huang et al. [16] only. The selection of the best element among the 64 available is very important: the accuracy reported in Table 1 for the proposed technique is the average obtained from all the 8 elements taken in the last row or column w.r.t. the direction of the 1-D DCT, as already stated before. A further improvement could be possible with a better and automated element selection method.

Finally, another test was carried out on images taken in the wild from the social network dataset [13]. Results are reported in Table 2 for 1-D DCT on vertical and horizontal directions. The best accuracy level is reported to be of 95% and demonstrates the effectiveness of the technique. Values for the first row and column are not reported being related to low frequency components that have no discriminative information.

Table 1. Results in terms of best accuracy obtained on the same UCID-derived dataset, between the best methods in the state-of-the-art compared to the proposed approach w.r.t. QF1-QF2 couples.
Full size table
Table 2. Accuracy results obtained for each coefficient on Giudice et al. [13] dataset. Best accuracy results come from elements in the last row and column for 1-D DCT on vertical and horizontal directions respectively and confirm the heatmaps described in Fig. 2b and c.
Full size table

8 Conclusions and Future Works

In this paper an in-depth analysis of the elements in \(8\times 8\) blocks of a JPEG image was carried out in the DCT domain with the aim of finding useful information to be exploited in the Double Quantization Detection problem. Through the analyses, the first digit statistics was employed with discriminative results in the highest frequency components (the last row or the last column) in the 1D-DCT transformed \(8\times 8\) blocks. Thus the first digit statistics was encoded as a feature for a simple Gradient Boost Classifier in order to be able to evaluate the detection effectiveness on synthetic couples of double compressed images and on images taken in the wild. Results demonstrated to outperform state-of-the-art methods in terms of accuracy, easiness, explainability and fastness of the technique.

Further investigation will be devoted to the formalization of the underlying mathematical law in order to build a self-explainable DQD technique; moreover it could be possible to exploit 1-D DCT Domain Analysis in order to detect tampered region in JPEG images.