Abstract
We analyse two translations from the synchronous into the asynchronous \(\pi \)-calculus, both without choice, that are often quoted as standard examples of valid encodings, showing that the asynchronous \(\pi \)-calculus is just as expressive as the synchronous one. We examine which of the quality criteria for encodings from the literature support the validity of these translations. Moreover, we prove their validity according to much stronger criteria than considered previously in the literature.
This work was partially supported by the DFG (German Research Foundation).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
As observed by a referee, the encodings
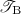 and
and 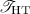 do not satisfy this constraint: the continuation process P can proceed before z is received. This issue could be alleviated by enriching the protocol with another communication from \(Q'\) to \(P'\).
do not satisfy this constraint: the continuation process P can proceed before z is received. This issue could be alleviated by enriching the protocol with another communication from \(Q'\) to \(P'\). - 2.
Gorla defines the latter concept only for languages that are equipped with a notion of structural congruence \(\equiv \) as well as a parallel composition |. In that case P has a top-level unguarded occurrence of \(\surd \) iff \(P\equiv Q|\surd \), for some Q [22]. Specialised to the \(\pi \)-calculus, a (top-level) unguarded occurrence is one that not lies strictly within a subterm \(\alpha .Q\), where \(\alpha \) is \(\tau \), \(\bar{x}y\) or x(z). For De Simone languages [42], even when not equipped with \(\equiv \) and |, a suitable notion of an unguarded occurrence is defined in [43].
References
Amadio, R.M., Castellani, I., Sangiorgi, D.: On bisimulations for the asynchronous pi-calculus. Theoret. Comput. Sci. 195(2), 291–324 (1998). https://doi.org/10.1016/S0304-3975(97)00223-5
Baldamus, M., Parrow, J., Victor, B.: A fully abstract encoding of the \({\pi }\)-calculus with data terms. In: Caires, L., Italiano, G.F., Monteiro, L., Palamidessi, C., Yung, M. (eds.) ICALP 2005. LNCS, vol. 3580, pp. 1202–1213. Springer, Heidelberg (2005). https://doi.org/10.1007/11523468_97
Beauxis, R., Palamidessi, C., Valencia, F.D.: On the asynchronous nature of the asynchronous \(\pi \)-calculus. In: Degano, P., De Nicola, R., Meseguer, J. (eds.) Concurrency, Graphs and Models. LNCS, vol. 5065, pp. 473–492. Springer, Heidelberg (2008). https://doi.org/10.1007/978-3-540-68679-8_29
Boudol, G.: Notes on algebraic calculi of processes. In: Apt, K.R. (eds) Logics and Models of Concurrent Systems. NATO ASI Series (Series F: Computer and Systems Sciences), vol. 13, pp. 261–303. Springer, Heidelberg (1985). https://doi.org/10.1007/978-3-642-82453-1_9
Boudol, G.: Asynchrony and the \(\pi \)-calculus (Note). Technical Report, 1702, INRIA (1992)
Brinksma, E., Rensink, A., Vogler, W.: Fair testing. In: Lee, I., Smolka, S.A. (eds.) CONCUR 1995. LNCS, vol. 962, pp. 313–327. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-60218-6_23
Cacciagrano, D., Corradini, F.: On synchronous and asynchronous communication paradigms. ICTCS 2001. LNCS, vol. 2202, pp. 256–268. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45446-2_16
Cacciagrano, D., Corradini, F., Palamidessi, C.: Separation of synchronous and asynchronous communication via testing. Theoret. Comput. Sci. 386(3), 218–235 (2007). https://doi.org/10.1016/j.tcs.2007.07.009
De Nicola, R., Hennessy, M.: Testing equivalences for processes. Theoret. Comput. Sci. 34, 83–133 (1984). https://doi.org/10.1016/0304-3975(84)90113-0
Du, W., Yang, Z., Zhu, H.: A fully abstract encoding for sub asynchronous Pi calculus. In: Pang, J., Zhang, C., He, J., Weng, J. (eds.) Proceedings of TASE 2018, pp. 17–27. IEEE Computer Society Press (2018). https://doi.org/10.1109/TASE.2018.00011
Fu, Y.: Theory of interaction. Theoret. Comput. Sci. 611, 1–49 (2016). https://doi.org/10.1016/j.tcs.2015.07.043
Given-Wilson, T.: Expressiveness via intensionality and concurrency. In: Ciobanu, G., Méry, D. (eds.) ICTAC 2014. LNCS, vol. 8687, pp. 206–223. Springer, Cham (2014). https://doi.org/10.1007/978-3-319-10882-7_13
Given-Wilson, T.: On the expressiveness of intensional communication. In: Borgström, J., Crafa, S. (eds.) Proceedings EXPRESS/SOS 2014. EPTCS, vol. 160, pp. 30–46 (2014). https://doi.org/10.4204/EPTCS.160.4
Given-Wilson, T., Legay, A.: On the expressiveness of joining. In: Knight, S., Lanese, I., Lluch Lafuente, A., Torres Vieira, H. (eds.) Proceedings of ICE2015. EPTCS, vol. 189, pp. 99–113 (2015). https://doi.org/10.4204/EPTCS.189.9
Given-Wilson, T., Legay, A.: On the expressiveness of symmetric communication. In: Sampaio, A., Wang, F. (eds.) ICTAC 2016. LNCS, vol. 9965, pp. 139–157. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-46750-4_9
van Glabbeek, R.J.: On the expressiveness of ACP. In: Ponse, A., Verhoef, C., van Vlijmen, S.F.M. (eds.) Algebra of Communicating Processes. Workshops in Computing, pp. 188–217. Springer, London (1995), https://doi.org/10.1007/978-1-4471-2120-6_8
van Glabbeek, R.J.: Musings on encodings and expressiveness. In: Luttik, B., Reniers, M.A. (eds.) Proceedings EXPRESS/SOS 2012. EPTCS, vol. 89, pp. 81–98 (2012). https://doi.org/10.4204/EPTCS.89.7
van Glabbeek, R.J.: On the validity of encodings of the synchronous in the asynchronous \(\pi \)-calculus. Inf. Process. Lett. 137, 17–25 (2018). https://doi.org/10.1016/j.ipl.2018.04.015. https://arxiv.org/abs/1802.09182
van Glabbeek, R.J.: A Theory of Encodings and Expressiveness. Technical Report, Data61, CSIRO (2018). https://arxiv.org/abs/1805.10415. Full version of [20]
van Glabbeek, R.J.: A theory of encodings and expressiveness (extended abstract). In: Baier, C., Dal Lago, U. (eds.) FoSSaCS 2018. LNCS, vol. 10803, pp. 183–202. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-89366-2_10
Gorla, D.: A taxonomy of process calculi for distribution and mobility. Distrib. Comput. 23(4), 273–299 (2010). https://doi.org/10.1007/s00446-010-0120-6
Gorla, D.: Towards a unified approach to encodability and separation results for process calculi. Inf. Comput. 208(9), 1031–1053 (2010). https://doi.org/10.1016/j.ic.2010.05.002
Gorla, D., Nestmann, U.: Full abstraction for expressiveness: history, myths and facts. Math. Struct. Comput. Sci. 26(4), 639–654 (2016). https://doi.org/10.1017/S0960129514000279
Honda, K., Tokoro, M.: An object calculus for asynchronous communication. In: America, P. (ed.) ECOOP 1991. LNCS, vol. 512, pp. 133–147. Springer, Heidelberg (1991). https://doi.org/10.1007/BFb0057019
Lanese, I., Pérez, J.A., Sangiorgi, D., Schmitt, A.: On the expressiveness of polyadic and synchronous communication in higher-order process calculi. In: Abramsky, S., Gavoille, C., Kirchner, C., Meyer auf der Heide, F., Spirakis, P.G. (eds.) ICALP 2010. LNCS, vol. 6199, pp. 442–453. Springer, Heidelberg (2010). https://doi.org/10.1007/978-3-642-14162-1_37
Milner, R.: The Polyadic \(\pi \)-Calculus: A Tutorial. Technical Report ECS-LFCS-91-180, The University of Edinburgh. Informatics Report Series (1991)
Milner, R.: Functions as processes. Math. Struct. Comput. Sci. 2(2), 119–141 (1992). https://doi.org/10.1017/S0960129500001407
Natarajan, V., Cleaveland, R.: Divergence and fair testing. In: Fülöp, Z., Gécseg, F. (eds.) ICALP 1995. LNCS, vol. 944, pp. 648–659. Springer, Heidelberg (1995). https://doi.org/10.1007/3-540-60084-1_112
Nestmann, U.: What is a “Good” encoding of guarded choice? Inf. Comput. 156(1–2), 287–319 (2000). https://doi.org/10.1006/inco.1999.2822
Nestmann, U., Pierce, B.C.: Decoding choice encodings. Inf. Comput. 163(1), 1–59 (2000). https://doi.org/10.1006/inco.2000.2868
Palamidessi, C.: Comparing the expressive power of the synchronous and asynchronous pi-calculi. Math. Struct. Comput. Sci. 13(5), 685–719 (2003). https://doi.org/10.1017/S0960129503004043
Parrow, J.: General conditions for full abstraction. Math. Struct. Comput. Sci. 26(4), 655–657 (2016). https://doi.org/10.1017/S0960129514000280
Peters, K., van Glabbeek, R.J.: Analysing and comparing encodability criteria. In: Crafa, S., Gebler, D.E. (eds.) EXPRESS/SOS 2015. EPTCS, vol. 190, pp. 46–60 (2015). https://doi.org/10.4204/EPTCS.190.4
Peters, K., Nestmann, U.: Is it a “Good” encoding of mixed choice? In: Birkedal, L. (ed.) FoSSaCS 2012. LNCS, vol. 7213, pp. 210–224. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-28729-9_14
Peters, K., Nestmann, U., Goltz, U.: On distributability in process calculi. In: Felleisen, M., Gardner, P. (eds.) ESOP 2013. LNCS, vol. 7792, pp. 310–329. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-37036-6_18
Peters, K., Schicke, J.-W., Nestmann, U.: Synchrony vs causality in the asynchronous pi-calculus. In: Luttik, B., Valencia, F. (eds.) Proceedings EXPRESS 2011, EPTCS, vol. 64, pp. 89–103 (2011). https://doi.org/10.4204/EPTCS.64.7
Quaglia, P., Walker, D.: On synchronous and asynchronous mobile processes. In: Tiuryn, J. (ed.) FoSSaCS 2000. LNCS, vol. 1784, pp. 283–296. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-46432-8_19
Riecke, J.G.: Fully abstract translations between functional languages. In: Wise, D.S. (ed.) Proceedings POPL 1991, pp. 245–254. ACM Press (1991). https://doi.org/10.1145/99583.99617
Sangiorgi, D., Walker, D.: The \(\pi \)-Calculus: A Theory of Mobile Processes. Cambridge University Press, Cambridge (2001)
Shapiro, E.Y.: Separating concurrent languages with categories of language embeddings. In: Koutsougeras, C., Vitter, J.S. (eds.) STOC 1991, pp. 198–208. ACM (1991). https://doi.org/10.1145/103418.103423
Shapiro, E.: Embeddings among concurrent programming languages. In: Cleaveland, W.R. (ed.) CONCUR 1992. LNCS, vol. 630, pp. 486–503. Springer, Heidelberg (1992). https://doi.org/10.1007/BFb0084811
de Simone, R.: Higher-level synchronising devices in Meije-SCCS. Theoret. Comput. Sci. 37, 245–267 (1985). https://doi.org/10.1016/0304-3975(85)90093-3
Vaandrager, F.W.: Expressiveness results for process algebras. In: de Bakker, J.W., de Roever, W.-P., Rozenberg, G. (eds.) REX 1992. LNCS, vol. 666, pp. 609–638. Springer, Heidelberg (1993). https://doi.org/10.1007/3-540-56596-5_49
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Additional information
This paper is dedicated to Catuscia Palamidessi, on the occasion of her birthday. It has always been a big pleasure and inspiration to discuss with her.
A Appendix: Boudol’s Translation is Valid up to
A Appendix: Boudol’s Translation is Valid up to 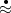
Before we prove validity of Boudol’s translation up to weak barbed bisimulation, we further investigate the protocol steps established by Boudol’s encoding. Let  and
and  . Pick u, v not free in P and Q, with
. Pick u, v not free in P and Q, with  . Then
. Then

Here structural congruence is applied in omitting parallel components \(\varvec{0}\) and empty binders (u) and (v). Now the crucial idea in our proof is that the last two reductions are inert, in that set of the potential behaviours of a process is not diminished by doing (internal) steps of this kind. The first reduction above in general is not inert, as it creates a commitment between a sender and a receiver to communicate, and this commitment goes at the expense of the potential of one of the two parties to do this communication with another partner. We employ a relation that captures these inert reductions in a context.
Definition 14
([18]). Let \(\equiv \!\Rrightarrow \) be the smallest relation on \(\mathcal {P}_{\mathrm{a\pi }}\) such that
-
1.
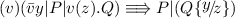 ,
, -
2.
if \(P\equiv \!\Rrightarrow Q\) then \(P|C \equiv \!\Rrightarrow Q|C\),
-
3.
if \(P\equiv \!\Rrightarrow Q\) then \((w) P\equiv \!\Rrightarrow (w) Q\),
-
4.
if \(P\mathrel {\equiv }P' \equiv \!\Rrightarrow Q' \mathrel {\equiv }Q\) then \(P\equiv \!\Rrightarrow Q\),
where  .
.
First of all observe that whenever two processes are related by \(\equiv \!\Rrightarrow \), an actual reduction takes place.
Lemma 3
([18]). If \(P \equiv \!\Rrightarrow Q\) then \(P \longmapsto Q\).
The next two lemmas confirm that inert reductions do not diminish the potential behaviour of a process.
Lemma 4
([18]). If \(P \equiv \!\Rrightarrow Q\) and \(P \longmapsto P'\) with  then there is a \(Q'\) with \(Q \longmapsto Q'\) and \(P' \equiv \!\Rrightarrow Q'\).
then there is a \(Q'\) with \(Q \longmapsto Q'\) and \(P' \equiv \!\Rrightarrow Q'\).
Corollary 3
If \(P \equiv \!\Rrightarrow ^* Q\) and \(P \longmapsto P'\) then either  or there is a \(Q'\) with \(Q \longmapsto Q'\) and \(P' \equiv \!\Rrightarrow ^* Q'\).
or there is a \(Q'\) with \(Q \longmapsto Q'\) and \(P' \equiv \!\Rrightarrow ^* Q'\).
Proof
By repeated application of Lemma 4. \(\square \)
Lemma 5
If \(P \equiv \!\Rrightarrow Q\) and \(P {\downarrow _{a}}\) for \(a \in \{ x, \bar{x} \,|\, x \in \mathcal N \}\) then \(Q {\downarrow _{a}}\).
Proof
Let \((\tilde{w})P\) for  with
with  denote \((w_1)\cdots (w_n)P\) for some arbitrary order of the \((w_i)\). Using a trivial variant of Lemma 1.2.20 in [39], there are \(\tilde{w} \subseteq \mathcal {N}\),
denote \((w_1)\cdots (w_n)P\) for some arbitrary order of the \((w_i)\). Using a trivial variant of Lemma 1.2.20 in [39], there are \(\tilde{w} \subseteq \mathcal {N}\),  and
and  , such that \(x\in \tilde{w}\) and
, such that \(x\in \tilde{w}\) and  . Since \(P{{\downarrow _{a}}}\), it must be that \(a{=}u\) or \(\bar{u}\) with \(u\notin \tilde{w}\), and \(C{{\downarrow _{a}}}\). Hence \(Q{{\downarrow _{a}}}\). \(\square \)
. Since \(P{{\downarrow _{a}}}\), it must be that \(a{=}u\) or \(\bar{u}\) with \(u\notin \tilde{w}\), and \(C{{\downarrow _{a}}}\). Hence \(Q{{\downarrow _{a}}}\). \(\square \)
The following lemma states, in terms of Gorla’s framework, operational completeness [22]: if a source term is able to make a step, then its translation is able to simulate that step by protocol steps.
Lemma 6
([18]). Let  . If \(P \longmapsto P'\) then
. If \(P \longmapsto P'\) then  .
.
Finally, the next lemma was a crucial step in establishing operational soundness [22].
Lemma 7
([18]). Let  and
and  . If
. If  then there is a \(P'\) with \(P \longmapsto P'\) and
then there is a \(P'\) with \(P \longmapsto P'\) and  .
.
Using these lemmas, we prove the validity of Boudol’s encoding up to weak barbed bisimilarity.
Theorem 4
Boudol’s encoding is valid up to  .
.
Proof
Define the relation \(\mathrel {\mathcal {R}}\) by \(P\mathrel {\mathcal {R}}Q\) iff  . It suffices to show that the symmetric closure of \(\mathrel {\mathcal {R}}\) is a weak barbed bisimulation.
. It suffices to show that the symmetric closure of \(\mathrel {\mathcal {R}}\) is a weak barbed bisimulation.
To show that \(\mathrel {\mathcal {R}}\) satisfies Clause 1 of Definition 8, suppose \(P \mathrel {\mathcal {R}}Q\) and \(P {\downarrow _{a}}\) for \(a \in \{ x, \bar{x} \,|\, x \in \mathcal N \}\). Then  by Lemma 1. Since
by Lemma 1. Since  , we obtain
, we obtain  by Lemma 3, and thus \(Q {\Downarrow _{a}}\).
by Lemma 3, and thus \(Q {\Downarrow _{a}}\).
To show that \(\mathrel {\mathcal {R}}\) also satisfies Clause 2, suppose \(P \mathrel {\mathcal {R}}Q\) and \(P \longmapsto P'\). Since  , by Lemmas 3 and 6 we have
, by Lemmas 3 and 6 we have  .
.
To show that \(\mathrel {\mathcal {R}}^{-1}\) satisfies Clause 1, suppose \(P \mathrel {\mathcal {R}}Q\) and \(Q {\downarrow _{a}}\). Since  , Lemma 5 yields
, Lemma 5 yields  , and Lemma 1 gives \(P {\downarrow _{a}}\), which implies \(P {\Downarrow _{a}}\).
, and Lemma 1 gives \(P {\downarrow _{a}}\), which implies \(P {\Downarrow _{a}}\).
To show that \(\mathrel {\mathcal {R}}^{-1}\) satisfies Clause 2, suppose \(P \mathrel {\mathcal {R}}Q\) and \(Q \longmapsto Q'\). Since  , by Corollary 3 either
, by Corollary 3 either  or there is a \(Q''\) with
or there is a \(Q''\) with  and
and  . In the first case \(P \mathrel {\mathcal {R}}Q'\), so taking \(P':=P\) we are done. In the second case, by Lemma 7 there is a \(P'\) with \(P \longmapsto P'\) and
. In the first case \(P \mathrel {\mathcal {R}}Q'\), so taking \(P':=P\) we are done. In the second case, by Lemma 7 there is a \(P'\) with \(P \longmapsto P'\) and  . We thus have \(P' \mathrel {\mathcal {R}}Q'\). \(\square \)
. We thus have \(P' \mathrel {\mathcal {R}}Q'\). \(\square \)
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this chapter
Cite this chapter
van Glabbeek, R., Goltz, U., Lippert, C., Mennicke, S. (2019). Stronger Validity Criteria for Encoding Synchrony. In: Alvim, M., Chatzikokolakis, K., Olarte, C., Valencia, F. (eds) The Art of Modelling Computational Systems: A Journey from Logic and Concurrency to Security and Privacy. Lecture Notes in Computer Science(), vol 11760. Springer, Cham. https://doi.org/10.1007/978-3-030-31175-9_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-31175-9_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-31174-2
Online ISBN: 978-3-030-31175-9
eBook Packages: Computer ScienceComputer Science (R0)


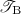 and
and 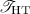 do not satisfy this constraint: the continuation process P can proceed before z is received. This issue could be alleviated by enriching the protocol with another communication from
do not satisfy this constraint: the continuation process P can proceed before z is received. This issue could be alleviated by enriching the protocol with another communication from 
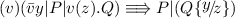 ,
,