1 Introduction

Determining the neural mechanisms underlying general intelligence is fundamental to understanding cognitive development, how this relates to real-world health outcomes, and how interventions (education, environment) might improve outcomes through adolescence and into adulthoodFootnote 1. Among different types of general intelligence, fluid intelligence is a major factor in measuring general intelligence [3], which can be measured via the NIH Toolbox Neurocognition battery [1] and from which demographic confounding factors (e.g., sex, and age) are removed. It is an emerging topic to use machine learning based methods to predict fluid intelligence from medical images via data-driven manner. However, direct prediction of fluid intelligence from the brain MRI Images is often challenging due to the lack of determinant factor. Furthermore, direct regression from the brain volumes is easy to overfit the training data with lower performance on testing samples.

In this paper, we develop a 3D convolutional neural network (CNN) based framework to predict the fluid intelligence from T1-weighted MRI images. The 3D CNN is able to fully incorporate the 3D information and geometric cues of the MRI images for effective fluid intelligence prediction. Although lack of determinate factor, intelligence is found to be significantly correlated with intracranial, cerebral, temporal lobe, hippocampal, and cerebellar volume [2]. Therefore, to improve the prediction accuracy, we propose to incorporate the morphological information into the framework for fluid intelligence prediction. In particular, we utilize an encoder-decoder regularization to facilitate the model to learn a more discriminative morphological feature by conducting the brain structure simultaneously. We propose a two-stage training scheme to train the whole framework. We first train an encoder-decoder-like network to conduct the brain structure segmentation task, and then we reuse the encoder part as the prediction network backbone to conduct the fluid intelligence prediction. In the first stage, we train the model using the MR brain volumes and its corresponding structure masks from the training and validation subset. By conducting the segmentation task, the network can learn a generalized feature for the fluid intelligence prediction. Next, we discard the decoder part and fine-tune the encoder part with an additional regression branch to predict the fluid intelligence value, in which the MR brain volumes and the fluid intelligence scores are used. The encoder part with the regression branch (blue part in Fig. 1) is used as our final 3D CNN architecture for fluid intelligence prediction. This two-stage training pipeline alleviates the overfitting problem of the network when directly regressing the fluid intelligence from MR images.

Fig. 1.
figure 1

The schematic illustration of the overall framework. The blue blocks and the white blocks denote the 3D convolutional layers in the encoder and decoder part, respectively. We then add an additional regression layer (blue dot) for the regression task. (Color figure online)

Full size image

2 Methodology

2.1 Network Architecture

Our proposed framework is based on 3D convolutional neural network to fully incorporate the 3D information of the MRI volumes. To improve the generality capability of network and learn more discriminative semantic features, we further utilize an encoder-decoder regularization scheme to train our model in a two-stage manner.

Figure 1 demonstrate the overall framework of our method. We first train an encoder-decoder-like architecture, which takes an MR brain volume as the input and outputs the segmentation result in an end-to-end manner. We use multiple convolutional layers to generate a set of 3D convolutional feature maps with multiple resolutions; see the blue blocks in the left part of Fig. 1. Then, the deepest highly semantic feature maps with the lowest resolution (the bottom row in Fig. 1) are repeatedly enlarged by the deconvolutional layers (decoder part) and concatenated with the corresponding feature maps from the encoder part via the skip connection. Next, we reconstruct the segmentation mask of the input volume, and update the weights in the encoder-decoder by calculating the cross-entropy loss between the predicted mask and the ground truth mask. The details of architecture is shown in Table 1.

Table 1. The network architecture of our proposed method. To reduce the size of feature maps, we set the stride of the first convolutional layer at each stage in the encoder path as 2. “” indicates a basic residual block (not bottleneck) in which the conv denotes a combination of a concolutional layer, a batch normalization layer and a relu activation layer. While fc denotes the fully-connected layer.
Full size table

In the second training stage, we discard the decoder part and fine-tune the learned weights in the encoder part. We further add a regression module behind the encoder, which contains one fully connected layer without any activation layer, to predict the intelligence score. We update the regression module by calculating the mean square error loss between the ground truth intelligence score and the predicted score.

2.2 Training Details

To accelerate the training process, we initialize the parameters of all the convolutional layers in our network with the “uniform” initialization method. We adopt the Adam optimizer [4] to optimize the network with a weight decay of 0.0001 and a batch size of eight for both the first and second training stages. We set the learning rate as 0.0001, and periodically reduce it by multiplying 0.9 in every 1, 000 iterations, and the training process is terminated after 10, 000 iterations without early stop for both stages. Our method is implemented with Tensorflow and DLTK toolbox [5].

3 Experiments

3.1 Dataset

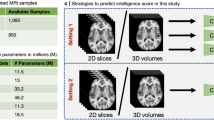
In the ABCD challenge dataset [6], the training, validation and testing subset contain 3739, 415 and 4402 individual subjects, respectively. Each subject contains a 3D MR brain volume and a corresponding structure segmentation mask, as shown in Fig. 2. These images are with the uniform volume size (\(240\times 240\times 240\)). Besides, the training and validation subset also have a pre-residual intelligence score for each individual subjects.

Fig. 2.
figure 2

Different views of the 3D Data samples (MR brain volumes and its segmentation masks) from training dataset.

Full size image

3.2 Data Pre-processing and Experimental Setup

To facilitate the training procedure, we conducted some pre-processing steps for each 3D brain volume. We first resized the brain volume to \(120\times 120\times 120\) using bilinear interpolation. Then we center cropped a \(120\times 120\times 90\) region from the resized volume, considering the z dimension contains less information than the x and y dimensions. We also performed “whitening” operation to normalize the intensity to zero mean and unit variance. To increase the total amount of training data and enhance the robustness of the network, we used random flipping and random cropping as data augmentation in the training process. Specifically, we randomly cropped a \(96\times 96\times 64\) region out \(120\times 120\times 90\) original brain volume as the input of the network during the training.

During the two-stage training process, we first use the brain volumes and its corresponding segmentation masks from training and validation subsets to train the encoder-decoder architecture without updating the regression part. In this step, we merged the labeled brain structures and regarded the segmentation as a binary segmentation task. In the second stage, we fixed the weights of the encoder part and update the regression part using the brain volume and the provided intelligence score. In the testing phase, we take the MR brain volume with the same pre-processing steps as input and directly output the regressed pre-residual intelligence score.

3.3 Evaluation Metrics and Results

Encoder-Decoder Segmentation Results. To validate whether the encoder-decoder learned the morphological features, we use dice coefficient score as the evaluation metric. The dice coefficient score computes the region based similarity between the predicted segmentation result and the ground truth segmentation mask:

$$\begin{aligned} Dice\left( P, G\right) = \frac{2 \times \left| P \cap G \right| }{\left| P \right| + \left| G \right| } \ , \end{aligned}$$
(1)

where P denotes the predicted segmentation result, G denotes the ground truth segmentation mask, \(\left| P \cap G \right| \) denotes the overlapped region between P and G, and \(\left| P \right| + \left| G \right| \) represents the union region. Noted, a larger Dice indicates a better segmentation result. Our trained encoder-decoder achieved a Dice of 0.9767 in the validation dataset. While in the testing dataset, we also achieved a similar Dice of 0.9465, which indicates the learned convolutional layers can extract discriminative features from MRI volumes.

Fluid Intelligence Prediction Results. In the testing/validation phase, we used the ten-crops to obtain the final results. Specifically, we randomly cropped ten regions (\(96\times 96\times 64\)) from the pre-processed images (\(120\times 120\times 90\)) and separately made a prediction for each region with the trained network. Then, we averaged the ten predicted scores as the final output score for one input image. With only the training dataset, our method achieved an MSE error of 71.5679 at the validation dataset. In the final testing phase, we merged the training volumes and validation volumes to the whole framework, and our method achieved an MSE error of 102.2498 on the testing data.

4 Conclusion

This paper presents a 3D convolutional neural network for fluid intelligence prediction from T1-weighted MRI images. We employ an encoder-decoder segmentation regularization to learn discriminative morphological feature of the brain volume for better fluid intelligence value prediction. The proposed two-stage framework can reduce the overfitting of the network when directly regressing fluid intelligence values. The proposed framework can be generalized to other related regression problems.