Abstract
Functional connectivity (FC) has been widely used to understand how the human brain works and to discover the neurobiological underpinnings of brain disorders in many neuroscience and clinical studies. Linear FC measures such as Pearson’s correlation have been widely used in functional neuroimaging studies that are based on the observed direct or indirect electrophysiological correlates within BOLD (blood oxygen-level dependent) signals. However, there is still much to be done in the area of methods development for separation of non-linear neural and non-neural sources of signal variation. In this paper, we address this fundamental issue with a novel data-driven approach to reveal the intrinsic and reproducible FCs via graph signal processing and graph learning techniques. Specifically, we regard BOLD signals from the whole-brain as graph signals that reside on the functional network. Then, we jointly smooth the BOLD signals in the context of the brain network and optimize the network connectivity by learning the graph Laplacian that represents the network spectrum for adaptive BOLD signal smoothing. We have evaluated our novel functional network construction method on simulated brain network data and resting-state functional magnetic resonance imaging data in the study of frontotemporal dementia (FTD). Compared with the conventional correlation based methods, our proposed learning-based method shows improvements in accuracy and greater statistical power.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Functional magnetic resonance imaging (fMRI) measures brain activity in vivo by detecting fluctuations associated with blood flow [1]. Since cerebral blood flow and neuronal activation are often coupled, converging evidence refers to the concept that functional connectivity (FC) is essential for understanding the organized behavior of cortical regions beyond the mapping of their activity [2].
Correlation of blood oxygen-level dependent (BOLD) signals is commonly used to measure the FC between two brain locations. The resulting correlation coefficients are usually converted to z-scores using the Fisher transformation and then thresholded to identify statistically significant network connections. The commonly used linear FC measures, such as Pearson’s correlation, bear the implicit assumption of Gaussianity of the dependence structures [3]. Although the correlation-based approach is efficient for assessing FCs from fMRI images, such gross simplification has limited power to quantify the complex whole brain connectivity. More critically, it is challenging to detect subtle fluctuations in neuronal BOLD signals in the presence of various non-neuronal noises, due to human physiological factors such as head motion and respiratory motion. Hence, it is a common practice to spatially smooth fMRI data using a low-pass filter for statistical analysis, at the cost of the reduced statistical power.
Graph theory has been extensively used to examine the properties of complex brain networks [1, 4]. In graph analysis, functional brain network can be defined as a graph where nodes may present voxels or brain regions and the links characterize the functional connectivities among nodes. Since FC measures can be affected by various non-neuronal factors such as spatial parcellation and noisy BOLD signal, thresholding becomes a standard procedure to filter the graph in order to maintain only those links whose link weights correspond to significant or strong FCs. However, there is an ongoing debate on how to find the optimal threshold. This is likely an issue that is partially responsible for the lack of reproducible functional network findings in the clinical neuroscience literature.
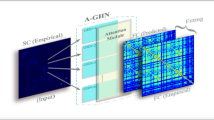
Suppose we assemble the time series of a BOLD signal at each region into a row-wise vector and assemble them into a data matrix, as shown in the red box of Fig. 1. In essence, current functional network construction approaches measure the strength of FC based on the row-wise correlation of the BOLD signals at one location to another, resulting in a symmetric connectivity matrix (also known as adjacency matrix). As shown in the bottom of Fig. 1, thresholding on the adjacency matrix is necessary to remove the spurious connections due to noise and keep the functional network sparse. Since it is challenging to characterize temporal coherence of brain activity by modeling the noisy BOLD signals, we propose to learn the network spectrum from the clean BOLD signals such that the learned functional network has enhanced power to capture the intrinsic FCs between brain regions.
Since BOLD signal value is associated with each brain region in the functional network, we evaluate BOLD signal at the same time period (i.e., each column in the data matrix) as a graph signal that supports the latent functional network [5], as shown in the pink box of Fig. 1. Without any constraint, there might be many solutions to associate a network to the observed BOLD signals. To resolve this issue, we constrain the solution space of functional networks by requiring that graph signals be smooth on the to-be-optimized functional network. Specifically, a graph signal being smooth means the BOLD signal values associated with two end vertices (connected brain regions) tend to be similar if the weight of the corresponding link is large, which is consistent with the current concept of weighted edges in functional brain networks. Leveraging the notion of graph smoothness, we present a graph learning framework that simultaneously adjusts BOLD signals and optimizes the graph Laplacian of the functional network until the connectivity in the learned network is consistent with the BOLD signals at all network vertices across each time point.
Figure 1 demonstrates the comparison between conventional correlation-based approach and our graph learning method. In general, the major contribution of our learning-based approach for functional networks has the following three folds. (1) Our work presents a framework to construct functional network by learning graph Laplacian. (2) As we will make it clear in Sect. 2, our method provides a principled way to adaptively smooth BOLD signals in the graph spectrum domain, which allows us to avoid over-smoothing BOLD signals caused by spatial low-pass or band-pass filters. (3) Our method can automatically remove the spurious connections by leveraging sparse representation technique in the learning process. This eliminates the need for thresholding and has the potential to enhance the reproducibility of functional network analyses.
We have evaluated the performance of our learning-based functional network construction method on both simulated fMRI data and real fMRI data from normal control (NC) and frontotemporal dementia (FTD) cohorts. Compared to the traditional correlation-based approaches, our learning-based method can significantly enhance the statistical power while maintaining the replicability in functional network analysis.
2 Method
Suppose a brain network consists of \( N \) nodes \( {\mathcal{V}} = \left\{ {v_{i} |i = 1, \ldots ,N} \right\} \). At every acquisition time \( t \) (\( t = 1, \ldots ,M \)), we arrange the whole-brain BOLD signal into a column vector \( \varvec{x}_{t} = \left[ {x_{t} \left( i \right)} \right]_{i = 1, \ldots ,N} \), where each element \( x_{t} \left( i \right) \) represents the BOLD signal value on node \( v_{i} \) at acquisition time \( t \). We further assemble the observed data matrix \( {\mathbf{X}} = \left[ {\varvec{x}_{t} } \right]_{t = 1, \ldots ,M} \) by stacking each \( \varvec{x}_{t} \) along the acquisition time \( t \). In conventional correlation based approach, the FC matrix \( {\mathbf{C}} = \left[ {c_{ij} } \right]_{i,j = 1}^{N} \) can be obtained by letting each element \( c_{ij} \) be the Pearson’s correlation between \( i^{th} \) row and \( j^{th} \) row in data matrix \( {\mathbf{X}} \). Next, we present how we learn the functional network by simultaneously de-noising BOLD signals and learning graph Laplacian from the clean graph signals.
Data Fitting Term.
Since one of our goals is to estimate the clean data matrix \( {\mathbf{Y}} = \left[ {\varvec{y}_{t} } \right]_{t = 1, \ldots ,M} \in R^{N \times M} \) from the observed \( {\mathbf{X}} \), it is reasonable to require the estimated \( {\mathbf{Y}} \) should be not too distinct from \( {\mathbf{X}} \), i.e., \( min\left\| {{\mathbf{X}} - {\mathbf{Y}}} \right\|_{F}^{2} \), which forms the data fitting term in our optimization.
Graph Smoothness Constraint.
Here, we use \( {\mathbf{W}} = \left[ {w_{ij} } \right]_{i,j = 1}^{N} \) denote for a \( N \times N \) adjacency matrix of the latent functional network, where each element \( w_{ij} \) characterizes the FC between node \( v_{i} \) and \( v_{j} \). Generally, the functional network can be encoded into a graph data structure \( {\mathbb{G}} = \left\{ {{\mathcal{V}},{\mathbf{W}}} \right\} \). Given \( {\mathbf{W}} \), the corresponding Laplacian matrix \( {\mathbf{L}} \) can be obtained by \( {\mathbf{L}} = {\mathbf{D}} - {\mathbf{W}} \), where \( {\mathbf{D}} \) is a diagonal matrix with \( {\mathbf{D}}_{ii} = \mathop \sum \limits_{j = 1}^{N} w_{ij} \). Intuitively, the Laplacian matrix measures the difference of connectivity flows between two nodes. The spectrum of brain network (encoded in the graph Laplacian matrix \( {\mathbf{L}} \)) allows us to examine the pairwise relationship between the clean BOLD signal value \( y_{t} \left( i \right) \) at \( v_{i} \) and \( y_{t} \left( j \right) \) at \( v_{j} \) in the context of functional connectivity. Specifically, we regard each \( \varvec{y}_{t} \) as a graph signal residing on the unanimous graph \( {\mathbb{G}} \) (shared by all \( \varvec{y}_{t} s \)). For example, \( {\mathbb{G}} \) is demonstrated by white lines and dots in the pink box of Fig. 1, where yellow and green denotes positive and negative values respectively. Although graph signals can be formed via numerous different combinations of \( \varvec{y}_{t} \) and \( {\mathbb{G}} \), it is more reasonable to seek smooth graph signals by adjusting \( \varvec{y}_{t} \) and optimizing \( {\mathbf{W}} \) simultaneously such that two connected nodes have similar scalar values along the corresponding connection defined in the underlying graph. Given \( {\mathbf{L}} \), the Laplacian quadratic form \( \left\| \varvec{Y} \right\|_{\varvec{L}}\; = \mathop \sum \limits_{t = 1}^{M} \varvec{y}_{t}^{T} {\mathbf{L}}\varvec{y}_{t} = \mathop \sum \limits_{t = 1}^{M} \mathop \sum \limits_{ij} w_{ij} \left( {y_{t} \left( i \right) - y_{t} \left( j \right)} \right) \) is used to measure the smoothness, i.e., \( \left\| \varvec{Y} \right\|_{\varvec{L}} \) is generally small when the majority of graph signals \( \varvec{y}_{t} \) have similar values at neighboring vertices connected by edges with large weights.
Note, the novel concept of smooth graph signal is consistent with the measurement of co-activation between brain regions in the current approach. As we will make it clear in Sect. 3, the main differences between our graph learning based method and conventional correlation based approaches are: (1) We iteratively reveal the functional network by examining the clean data matrix \( {\mathbf{Y}} \) column by column, while the conventional approach just measures FCs by row-wise correlations in the observed data matrix \( {\mathbf{X}} \). (2) We jointly estimate the FCs in the entire functional network, while conventional methods use a massively univariate procedure to calculate each FC separately. Thus, our method is a multivariate method that accounts for associations across the entire network while traditional univariate methods treat each edge as an independent outcome.
Regularization Term on Graph Laplacian Matrix.
To regularize the graph Laplacian \( {\mathbf{L}} \), we apply matrix Frobenius norm \( \left\| {\mathbf{L}} \right\|_{F}^{2} \) as well as the trace norm constraint (i.e., \( tr\left( {\mathbf{L}} \right) = N \)) to guarantee \( {\mathbf{L}} \) is valid Laplacian matrix.
Overall Energy Function.
By combining the data fitting term, graph smoothness term, and the regularization term, the overall energy function for learning the functional network is:
where \( \alpha \) and \( \beta \) are the scalars controlling the strength of \( \left\| \varvec{Y} \right\|_{\varvec{L}} \) and \( \left\| {\mathbf{L}} \right\|_{F}^{2} \), respectively.
3 Optimization
Although the energy function in Eq. 1 is not convex, we can alternatively optimize \( {\mathbf{Y}} \) and \( {\mathbf{L}} \), as estimating either \( {\mathbf{Y}} \) and \( {\mathbf{L}} \) alone falls into the scenario of convex optimization.
Smooth Graph Signals by Graph Filtering.
Discarding terms unrelated to \( {\mathbf{Y}} \), the energy function of optimizing the clean data matrix \( {\mathbf{Y}} \) becomes:
which is a classic Tikhonov regularization problem [6]. We have the closed form solution as:
where \( {\mathbf{I}} \in {\mathbb{R}}^{N \times N} \) is an identity matrix.
The intuition behind Eq. 3 can be interpreted as filtering the BOLD signals \( {\mathbf{X}} \) via the latent graph spectrum encoded in \( {\mathbf{L}} \). In graph signal processing [7], filtering a graph signal \( \varvec{y}_{t} \) by a filter \( h \) is defined as the operation:
where \( \left\{ {\varvec{u}_{l} ,\lambda_{l} } \right\} \) are eigenvector-eigenvalue pairs of \( {\mathbf{L}} \) and \( \tilde{\varvec{x}}_{t}^{l} = \varvec{u}_{l}^{T} \varvec{x}_{t} \) is the graph Fourier representation of \( \varvec{x}_{t} \) w.r.t graph frequency \( \lambda_{l} \). In this regard, our learning-based method offers a new window to smooth the BOLD signals via the learned smoothing kernel \( h \) which is defined in the graph spectrum domain as: \( h\left( {\lambda_{l} } \right) = \frac{1}{{1 + \alpha \lambda_{l} }} \). Specifically, we represent each graph Fourier representation \( \tilde{\varvec{x}}_{t} \) as a linear combination of complex exponentials. To that end, \( h\left( {\mathbf{L}} \right) = \left[ {\left( {\begin{array}{*{20}c} {h\left( {\lambda_{1} } \right)} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {h\left( {\lambda_{N} } \right)} \\ \end{array} } \right)} \right] \) is a low-pass filter that amplifies the contributions of low-frequency components and attenuates those of high-frequency components, where the frequency domain is characterized by graph Laplacian \( {\mathbf{L}} \).
Learn Graph Laplacian.
Given \( {\mathbf{Y}} \), we can optimize \( {\mathbf{L}} \) by minimizing \( \alpha \left\| {\mathbf{Y}} \right\|_{\varvec{L}} + \beta \left\| {\mathbf{L}} \right\|_{F}^{2} \). Considering all elements in \( {\mathbf{W}} \) are non-negative, it is relatively easier to search for a valid adjacency matrix \( {\mathbf{W}} \), instead of \( {\mathbf{L}} \), as:
where \( \gamma = \beta /\alpha \) controls the sparsity of \( {\mathbf{W}} \). Note for \( \gamma = 0 \) we have a very sparse solution that assigns weight \( s \) to the edge corresponding to the smallest pairwise distance in \( {\mathbf{Y}}^{T} {\mathbf{WY}} \) and zero everywhere else. On the other hand, we intend to penalized large degrees in the node degree vector \( {\mathbf{W}}1 \) as setting \( \gamma \) to big values, and in the limit \( \gamma \to \infty \), we obtain a dense adjency matrix \( {\mathbf{W}} \) with a constant degree. Since the energy function in Eq. 5 is in quadratic form with additional condition \( \left( {\left\| {\mathbf{W}} \right\|_{1}^{1} = N} \right) \), we first convert Eq. 5 to an augmented Lagrangian function with KKT (Karush Kuhn Tunker) multipliers [8] and then optimize \( {\mathbf{W}} \) using the classic ADMM (Alternating Direction Method of Multipliers) [9].
4 Experiments
In the following experiments, we first evaluate the accuracy and robustness of our graph learning method for functional networks using the simulated dataset. Second, we demonstrate the augmented statistical power of our learning-based functional network construction method in the FTD biomarker discovery studies. Results from our method are compared to conventional correlation based functional networks. In each experiment, we use grid search in increments of 0.1 to determine the combination of parameters \( \alpha \) and \( \beta \) that yields the lowest cost in Eq. 1 across randomly selected samples.
4.1 Evaluate the Accuracy and Robustness on the Simulated Dataset
Due to the lack of ground truth, we generate a set of simulated BOLD signals by introducing uncorrelated additive Gaussian noise to the original BOLD data matrix of an individual subject. Specifically, we introduce the noise to each element of data matrix independently. For the conventional method, we apply Gaussian low pass filter and then calculate the pairwise Pearson’s correlation coefficients based on the temporally smoothed BOLD signals. Our graph learning based method can simultaneously de-noise the BOLD signal and optimize functional network via the learned graph Laplacian. Considering the functional network constructed based on the correlations of original BOLD signals as the reference, we can quantitatively compare the residual of functional networks and the recovery of BOLD signals between the conventional method and our proposed method.
Figure 2(a) shows the curves of average PSNR (peak signal-to-noise ratio) between the original and the noisy BOLD signal (in black), the smoothed BOLD signal by Gaussian filter (in blue), and the recovered BOLD signal by graph filtering in Eq. (3) (in red), respectively. Since our learning-based method can utilize network priors to adaptively smooth the BOLD signals, our graph filtering process achieves the largest PSNR ratio at all noise levels. Furthermore, we evaluate the robustness of our graph learning approach by calculating the \( \ell_{2} \)-norm matrix distance between the FC matrices constructed with original BOLD signals and noisy BOLD signals at different noise levels, as the red curve shown in Fig. 2(b). Compared to the corresponding matrix distance plot by using conventional Pearson’s correlation coefficient (blue curve), the estimated functional network by our graph learning method is more stable (i.e., smaller matrix distance) against noise.
4.2 Evaluation on Population Network Analyses
This experiment consists of 103 NC and 78 FTD subjects from Neuroimaging in Frontotemporal Dementia (NIFD) database, each with T1-withed MR image and resting-state fMRI data. First, we parcellated each T1 image into 90 regions using AAL template. Thus, all functional networks are constructed based on 90 mean time course of BOLD signals. After the grid search, we fixed \( a = 0.1 \) and \( \beta = 1.0 \). The running time for constructing each functional connectivity matrix is less than one minute in PC.
Since the quality of functional network highly depends on the BOLD signals, we selected two brain regions (hippocampus and mid frontal lobe) and display the frequency spectrums (using Fourier transform) and signals of original BOLD (black), smoothed BOLD using Gaussian (blue), and recovered BOLD by our graph learning approach (red) in the top of Fig. 3. Although the Gaussian smoothing and our graph filtering both use low-pass filter, our method has more capability to maintain the detail than Gaussian smoothing, as the spectrum curve of harmonic magnitudes (red) by our method is apparently above the spectrum curve (blue) by Gaussian smoothing. After visually inspecting the recovered BOLD signals, we find that the smoothing results by both methods are very similar when the BOLD signal is relatively stable. However, our method can maintain much more intrinsic changing patterns (shown in the zoom-in view 1–4) than Gaussian smoothing when BOLD fluctuations occur. The functional networks estimated using Pearson’s correlation coefficients on the original BOLD signals (in the blue box) and our graph learning approach (in the red box) are shown in the bottom of Fig. 3. It is apparent that we obtain networks with clear modular structure without needing to select a thresholding parameter.
Top: The frequency spectrums of original BOLD signal, smoothed BOLD signal by Gaussian filter, and recovered BOLD signal by our graph filtering from four typical regions are displayed in black, blue and red, respectively. Bottom: Functional networks estimated by Pearson’s correlation coefficients (in the blue box) and our graph learning method (in the red box). Note, blue and red indicate the low and high connectivity strength, respectively. (Color figure online)
To assess the statistical significance of each method, we use a permutation test to create a null distribution of correlations. Specifically, we hold the FC constant and shuffle the diagnostic labels to break the linkage of network features and the clinic outcome. We apply 1000 permutations to each link of FC matrices calculated using Pearson’s correlation and that of using our graph learning method. By setting \( p < 0.05 \), the conventional method only finds one significant link of R. Insula and R. Paracentral lobule (in frontal lobe). Figure 2(c) shows in total seven functional connections (including the above significant link detected by using Pearson’s correlation) that have significant difference between NC and FTD cohorts by using our method. Most of the significant network differences occur in frontal and temporal lobes, which is consistent with the current neurobiological findings.
5 Conclusions
We presented a novel graph learning framework to characterize functional network from functional neuroimaging data. Compared to the conventional correlation based approach, our method can simultaneously clean the BOLD signal and learn the functional network in the spectrum of graph Laplacian. As a data-driven approach, our method is free of thresholding, which offers the potential to enhanced replicability of functional network analysis. We have evaluated our learning based functional network construction method in both the individual level and group comparison. The promising results show great potential of our method in current neuroimaging studies.
References
Sporns, O.: Networks of the Brain. The MIT Press, Cambridge (2011)
Lindquist, M.A.: The statistical analysis of fMRI data. Stat. Sci. 23, 439–464 (2008)
Hlinka, J., Palus, M., Vejmelka, M., Mantini, D., Corbetta, M.: Functional connectivity in resting-State fMRI: is llinear correlation sufficient. Neuroimage 54, 2212–2225 (2011)
Rubinov, M., Sporns, O.: Complex network measures of brain connectivity: uses and interpretations. Neuroimage 52, 1059–1069 (2010)
Shuman, D.I., Narang, S.K., Frossard, P., Ortega, A., Vandergheynst, P.: The emerging field of signal processing on graphs: extending high-dimensional data analysis to networks and other irregular domains. IEEE Signal Process. Mag. 30, 83–98 (2013)
Elmoataz, A., Lezoray, O., Bougleux, S.: Nonlocal discrete regularization on weighted graphs: a framework for image and manifold processing. IEEE Trans. Image Process. 17, 1047–1060 (2008)
Shuman, D., Narang, S., Frossard, P., Ortega, A., vandergheynst, P.: The emergence field of signal processing on graphs. IEEE Signal Process. Mag. 30, 83–90 (2013)
Boyd, S., Vandenberghe, L.: Convex Optimization. Cambridge University Press, New York (2004)
Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 3, 1 (2011)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Kim, M., Moussa, A., Liang, P., Kaufer, D., Larienti, P.J., Wu, G. (2019). Revealing Functional Connectivity by Learning Graph Laplacian. In: Shen, D., et al. Medical Image Computing and Computer Assisted Intervention – MICCAI 2019. MICCAI 2019. Lecture Notes in Computer Science(), vol 11766. Springer, Cham. https://doi.org/10.1007/978-3-030-32248-9_80
Download citation
DOI: https://doi.org/10.1007/978-3-030-32248-9_80
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-32247-2
Online ISBN: 978-3-030-32248-9
eBook Packages: Computer ScienceComputer Science (R0)