Keywords

1 Introduction

Multimodality feature fusion commonly used to combine multiple modality imaging, depicting and comprehending the interplay between anatomy and functions [1]. A variety of approaches have been used to address such issue, such as hierarchical supervised local canonical correlation analysis, manifold regularized multitask feature learning [2] and so on. However, these studies usually confront the challenge of deviation from data registration of multimodalities [3]. In addition, these studies merely based on single spatial scale information while some recent studies have covered that brain’s spatial structure is in the character of multi-scale which spans from individual voxels up to that of the whole brain [4], and that would provide more comprehensive information for brain research. Several studies have constructed features using multi-scale information, e.g., Hierarchical Model and X (HMAX) and Convolutional Neural Networks (CNN). These methods adopt multi-scale information to realize brain states decoding [5]; besides, Wang et al. employed a multi-scale clustering methodology known as ‘data cloud geometry’ to construct multi-scale features from functional connectivity patterns, and successfully distinguished autism spectrum disorders (ASD) from typical development (TD) participants [6]. Hence, how to decode brain information from multiscale angle and take advantage of single modality data deeply is an urgent issue.

Graph Signal Processing (GSP) methods are inherently capable to process activation patterns of brain on the irregular structural graph (e.g. functional connectivity or ROIs connection) [7]. They unite algebraic and spectral graph theoretic concepts in which exploring the interplay between activation pattern and functional connectivity development. For instance, the GSP method was used to study the stages of people learning process, the results showed that the contribution of brain activity signal to learning phases varies with the graph (connection of brain regions) spectral frequency [8]. In addition, this method, as one of the GSP methods, equips with multi-scale property, and was used to depict pupils’ social status in school by constructing multi-scale community detection [9]. However, the feature fusion method of multi-scale information extracted from graph signal has not been proposed, although these advantages have potential to be used for classification of brain states, diagnosis of diseases, or understanding of cognitive processes.

Motivated by the fundamental idea of Scale-Invariant Feature Transform (SIFT) method, which outperforms for constructing features of different scales, and GSP, which used for detecting the relationship between brain function and structure, we proposed a novel unite Graph Signal Wavelet transform Multi-scale framework (GSWM) to fuse activational-connectional information, for constructing features that could help to better understand cognition, aging, disease, and behavior of human. In this paper, we took multiple task functional magnetic resonance (fMRI) data from the Human Connectome Project (HCP) as our dataset. We decoded various brain states by features constructed by the GSWM framework, Softmax and L-SVM classifiers were used for measuring the prediction capability of the method. The results showed that our GSWM scheme had obvious advantages in decoding performance over such based on activation mode only. In addition, the multi-scale features obtained by GSWM method had the performance as good as the best classification performance of single-scale graph signal wavelet, and based on GSWM method, it was not necessary to bother to select the most particular suitable scale for optimization. Furthermore, the multi-scale features description can also assistant to apprehend the mechanism of brain cognition.

2 Method

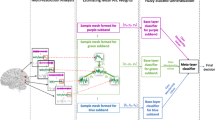
With functional magnetic resonance (fMRI) images, we firstly divided brain into 360 regions of interest (ROIs) (consistent with the partition template from HCP) to calculate functional connectivity, then averaged activation value of ROIs to constitute the signal on graph. Afterwards, wavelet transform processing method for graph signal was used to obtain multi-scale information of brain. Subsequently, we fused multi-scale information so as to generate multi-scale features for further brain states decoding. The GSWM processing framework is shown in Fig. 1.

Fig. 1.
figure 1

Features constructed by Graph wavelet Multi-Scale (GSWM) framework. (a) Graph signal constituted two parts: the signal made up by the value of vertex on graph, and the latent graph (functional connectivity here); (b) Wavelet matrix obtained by graph signal wavelet, each row contains 360 vertex (ROI) and each column contains 20 scales; (c) Feature construction: finding key points and calculating gradients around the key points; (d) Constructing Multi-scale features in each datasets.

Full size image

2.1 Data Description and Image Processing

We used fMRI data released by Human Connectome Project (HCP) (http://humanconnectomeproject.org) as our testbed. In which, 100 subjects, who have been scanned all tasks’ fMRI completely, were collected randomly for training and testing classifiers in our study. All subjects had normal or corrected-to-normal vision and no neurological and psychiatric history. Six different task fMRI data were collected for each subject, including working memory, gambling, language, social cognition, relational processing and emotion processing, and each task included several stimulation conditions.

The data were preprocessed with the HCP fMRI Surface pipeline and the beta map for each condition was produced and mapped to the standard CIFTI gray ordinates space. Given the fMRI images, various contrast maps with corresponding brain states for subsequent classification were defined. We compared each task condition with a baseline condition, and acquired contrast maps corresponded to the task condition. 14 kinds of cognitive stimuli constructed dataset 1. In addition, we constructed dataset 2 by picking up four stimuli types of working memory task (for the detailed tasks information please see supplementary Table 1).

Table 1. Decoding performance (classification accuracy) of three kinds of features
Full size table

2.2 Multi-scale Graph Wavelet Transform

Graph Signal Constructing:

Graph signal consists of two components, one is underlying graph structure (here it indicates the functional connectivity, which has been sparsed by setting value of edge on graph to 1 when the significance bigger than threshold), the other is signal composed by the values of each vertex (here it is the activation pattern of ROIs), and Graph Laplacian matrix was a bridge to fuse them by generating transform basis for further graph wavelet transform. Graph Laplacian matrix could be written as:

$$ L = D - W $$
(1)

where \( D \in {\mathbf{\mathcal{R}}}_{ + }^{n \times n} \) is the degree matrix, which sums the weights that connects to a certain ROI (vertex), \( \varvec{W \in R}^{{\varvec{n \times n}}} \) represents functional connectivity matrix, \( n \) is the number of ROIs, which is equal to the vertex number of graph.

After decomposing the Graph Laplacian matrix into eigenvector and eigenvalues, we obtain a symmetry matrix from functional connectivity so that it has a complete set of orthonormal eigenvectors. Eigenvector and eigenvalues could be written as follows:

$$ Lu_{l} = \lambda_{l} u_{l} $$
(2)

Hence the \( \varvec{ u}_{\varvec{l}} \) can be viewed as the graph spectral components, and the eigenvalues \( \varvec{\lambda}_{\varvec{l}} \) are graph frequencies, the \( u_{l} \) is the eigenvector corresponding to \( \varvec{\lambda}_{\varvec{l}} \). The larger the eigenvalue is, the larger the fluctuation of the eigenvector is. Due to the graph structure is obtained according to the functional connectivity, the decomposition of Laplace matrix is equivalent to decomposing the graph structure into several basic connection states from small to large fluctuations.

Multi-scale Graph Signal Wavelet:

Graph signal wavelet, which combines underlying connection and functional activation pattern, was used to extract multi-scale information. Wavelet transform possesses the merit of pinpointing in both temporal and spectral dimensions. Due to the graph signal was obtained by lining the activation of the vertexes (each vertex indicate a ROI) in graph, the wavelets could precisely locate a certain ROI.

Here we use spectral graph wavelet transform [10] providing wavelet kernel, which is derived from graph Fourier transform, to obtain multi-scale wavelet coefficients. The graph wavelet transform is defined by:

$$ W_{f} \left( {t,n} \right) = \sum\nolimits_{l = 0}^{N - 1} {g\left( {t\lambda_{l} } \right)f\left( l \right)u_{l} \left( n \right)} $$
(3)

where \( \varvec{f} \) is the signal on graph, \( \varvec{f}\left( \varvec{l} \right) \) is the l-th value on the signal and N is the number of vertexes. The latter two terms of the formula multiplying graph signal by eigenvector decomposed from graph Laplacian matrix correspond to graph Fourier transform, if the changing tendency of both are similar, the amplitude at the frequency (eigenvalue) is greater and vice versa. The \( \varvec{g}\left( {\varvec{t\lambda }_{\varvec{l}} } \right) \) is the wavelet kernel at \( \varvec{t} \) scale, and \( \varvec{W}_{\varvec{f}} \) is the wavelet coefficients which we use to construct multi-scale features further. We calculate the maximum eigenvalue and divide the eigenvalue into 20 pieces as 20 scales with log, which was the identical approach with [10]. Graph wavelet transform was obtained by multiplying graph Fourier transform with multi-scale kernels designed to achieve localization in the limit of fine scales. This allows us to observe the relative changes of brain activation corresponding to the underlying connectivity basis at multiple scales. The kernel in this paper was designed similarly to [10].

2.3 Multi-scale Information Combination

The principle of scale-invariant feature transform is detecting and describing local features in images. In our study, we defined key points by detecting local maximum and minimum through two-dimensional multi-scale images rather than three-dimensional like SIFT features, and described key points by calculating gradient around them. More concretely, the wavelet sequences obtained by multi-scale graph wavelet transform are arranged into two-dimensional matrices in order, and the local (the center points are compared with eight points in its 3 \( \times \) 3 neighborhood) maximum and minimum points in the matrix are selected as key point. Thus, most informative scale can be detected and pinpointed.

As for describing local information of key points, we integrate local information across scales to obtain descriptors of key points. Specifically, we calculated the gradient amplitude of nine points (centered on the key points as 3 \( \times \) 3 matrix) in eight gradient directions at intervals of 45°. In this way, we captured the change tendency of information between scales and ROIs, so that we got the descriptor for multi-scale information. Procedures could be summarized as follows:

figure a

We evaluated the decoding capability of multi-scale according to their prediction accuracy. Specifically, the prediction accuracy was obtained from the mean prediction accuracy based on the ten-fold cross validation. The performance of the GSWM feature construction framework was examined under two datasets 1 and 2.

3 Results

3.1 Interpretation of GSWM Features

After obtaining the multi-scale graph signal wavelet, we find the key points in the wavelet matrix. Several scales with dense key points were picked out and shown in Fig. 2. The results show that the key points are mainly concentrated in the 16-20 scales. The distributions of key points from datasets 1 and 2 are relatively close, scattering over a large part of the more advanced cortex such as prefrontal cortex, parietal lobe, and less in occipital lobe, which is most responsible for primary cognitive functions. That is perhaps because these tasks are more complex that need more advanced executive brain regions and such processing, e.g., the brain areas marker of working memory, i.e., prefrontal cortex, which is also the brain hub area associated with language tasks.

Fig. 2.
figure 2

Key points of both datasets distributions on brain.

Full size image

Besides, we constructed multi-scale feature vectors and calculated the gradient and direction weights of nine points with the key points as the center. Due to the direction of gradient is fixed artificially, weight is an important index for us to understand information differences in depth, and the gradient weights of the nine points are preserved as multi-scale features. We got the information exchange relationship between the adjacent frequencies and scales. That helped us figure out the information conversion between high and low frequencies and among different scales. Figure 3. showed the multi-scale feature vectors of an ROI in the prefrontal lobe and eight nodes around it (from three different scales). We can see that the changes of energy in different scales and brain regions are different, which may help us to have a deeper understanding of the switching mechanism between brain networks.

Fig. 3.
figure 3

Multi-scale features obtained by GSWM framework. Note that the vertex equals to ROI. Here, the gradients of 9 nodes around the key node in 8 directions are showed, which can depict the information difference between different nodes (ROIs) at different scales. This features from the working memory task with the stimuli of face.

Full size image

3.2 Effectiveness and Robustness of GSWM

We separately used two datasets to evaluate the decoding performance of our multi-scale features, and prediction accuracy was used as a measurement for the effectiveness and robustness of our GSWM framework. For comparison, activation pattern of 360 ROIs was used to decoding too, the prediction accuracy of datasets 1 and 2 were lower than the other two kinds of features (Fig. 4 and Table 1). Besides, the results could be seen in Fig. 4, the performance of GSWM features was similar to that of the best performance in single scale features, which was close to 100% in both datasets. This also showed that the information obtained by using the combination of underlying connection and functional activation patterns could effectively distinguish different cognitive tasks and retain more comprehensive information. In addition, the best performance scales of single scale feature on different datasets are different, while multi-scale feature can achieve good results without entanglement in selecting the best scale.

Fig. 4.
figure 4

Classification accuracy. (a) and (b) show the performance of accuracy using Softmax as the classifier; (c) and (d) use the L-SVM as the classifier; The blue bars indicate the performance of single scale graph wavelets; the orange bars indicate features derived by GSWM.

Full size image

3.3 Stabilization of the Features Derived by GSWM

For testing the stabilization of the GSWM features in keeping useful information and decoding brain states, we examined the prediction performance across different classifiers. Using similar two datasets and framework, we put these features into Softmax and Linear Support Vector Machine (L-SVM) classifiers, prediction accuracy were shown in Table 1. These results showed the advantage of the GSWM framework for combining comprehensive information and distinguishing different brain states effectively in both classifiers. Besides, it also indicates that the information differences cross different scales and ROIs in brain is meaningful not only in cognition understanding but also in further application, such as decoding.

4 Discussion and Conclusion

We presented a novel framework to fuse multi-scale information obtained by graph signal wavelet transform, named as GSWM, which banded both activation pattern in structure and functional connectivity. The multi-scale features described the local tendency of information differences, and our results showed that the multi-scale features obtained by GSWM method have excellent prediction performance, and based on GSWM, the problem of choosing scale does not exist. The results also proved the necessity of combining activational-connectional information. In addition, capturing local information contributes to the understanding of information differences in multi-scale brain networks. In the future, we will further use this framework to decode what pictures the subjects see during the tasks, instead of only classifying brain states.