Abstract
For complex congenital heart disease (CHD) involving a single functioning ventricle, the Fontan operation is performed which results in a circulation where deoxygenated venous blood passively flows into the pulmonary arteries without a ventricular pump. However, conventional Fontan graft designs may result in suboptimal cardiovascular hemodynamics leading to post-surgical complications. Patient-specific designs are thus promising in the Fontan operation. This paper reports the virtual simulation and designs of patient-specific Fontan grafts with the aid of computational fluid dynamics (CFD). CFD parameters including meshing, wall layers, and solver choices were studied to bolster accuracy while minimizing computational time. CFD simulations of original Fontan design were performed to evaluate three hemodynamic parameters: indexed power loss (iPL), hepatic flow distribution (HFD), and percentage of the non-physiological wall shear stress (%WSS, a novel surrogate marker for clot risk). New designs were then created to target these parameters with iterative optimization technique. This overall approach was utilized to redesign the Fontan grafts of patients (n = 2). The re-designed Fontan grafts showed significant improvements in all three hemodynamic parameters when compared to the original designs. Our unique integration of surgical design and flow simulation has the potential to enable cardiac surgeons to effectively simulate patient specific designs for the Fontan operation, potentially improving the surgical outcomes of patients with complex CHD.
This work is supported by the National Institutes of Health under award numbers R01HL143468 and R21HD090671. The content is solely the responsibility of the authors and does not represent the official views of the National Institutes of Health.
The authors acknowledge the University of Maryland supercomputing resources (http://hpcc.umd.edu) made available for conducting the research reported in this paper.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
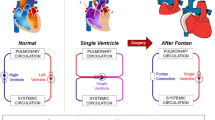
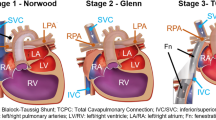
Congenital heart disease (CHD) affects 0.8% of the population, with \(\frac{1}{4}\) of infants requiring life-saving intervention as a neonate [9]. For patients with complex CHD involving a single functioning ventricle, surgeons perform a series of open-heart surgeries to modify the venous circulation. The third surgery, the Fontan operation, connects the inferior vena cava into the superior cavopulmonary anastomosis via intracardiac patch (lateral tunnel Fontan) or a conduit (extracardiac Fontan) [6]. The Fontan graft’s geometry influences hemodynamics of blood flow into the pulmonary arteries, and novel designs such as a y-shaped (bifurcated) graft have been previously proposed [11]. Despite significant development in the Fontan operation, graft designs are still constrained by material type and availability, potentially resulting in suboptimal cardiovascular hemodynamics and post-surgical complications including cardiac performance impairment [1], pulmonary arteriovenous malformation [14], and thrombosis [8]. Many studies approached this problem via simulating the blood flow inside Fontan and predicting hemodynamics using the computational fluid dynamics (CFD) [7, 13], none have addressed the risk of thrombosis in a Fontan graft.
The simulation approach can be combined with a manufacturing process using computer-aided design (CAD), CFD and electrospinning of tissue-engineered vascular grafts (TEVGs) to create patient-specific designs as part of virtual surgical planning [13]. With the use of these, patient-specific Fontan graft designs may be the key to improving the quality of surgery and patient outcomes. As patient-specific Fontan grafts become closer to reality, we continue to refine the workflow of virtual surgical planning by identifying an accurate, time-efficient and clinically relevant CFD approach to virtual surgical planning of Fontan grafts. The objective of this study is to investigate and propose the best set of CFD parameters (i.e. meshing strategy, wall layering, and CFD solver choice) for the Fontan circulation simulation. Additionally, along with CFD simulation of conventional hemodynamic parameters such indexed power loss and hepatic flow distribution (CFD), we introduce a novel hemodynamic parameter, non-physiological wall shear stress, that acts as a surrogate for risk of thrombosis.
2 Methods
This section summarizes the sequential steps for simulating and optimizing the Fontan designs. Our approach consists of seven steps (see Fig. 1) including two previously reported steps on manufacturing and implanting patient specific 3D printed grafts [5], which we will combine in the future for improving Fontan surgeries. Sections 2.1 and 2.2 entails the methods for MRI data acquisition (i.e. anatomy and boundary flow data), image segmentation, and geometry preparation. Section 2.3 lays out the details of the CFD simulation (i.e. meshing, number of wall layers, and solver settings). Based on the calculated hemodynamics, various Fontan design parameters are optimized in three iterations to correct the flow and pressure in the graft, which is explained in Sect. 2.4.
2.1 Data Acquisition and Image Segmentation
The magnetic resonance angiogram (MRA) data, consisting of a late-phase, nongated, breath-held acquisition with pixel size \(\sim \) \(1.4\times 1.4\) mm, served as a roadmap to build a 3-dimensional (3D) Fontan model, including the proximal cavae and branch pulmonary arteries, using a commercially available image segmentation software (Mimics; Materialise, Leuven, Belgium). Both automatic thresholding and manual methods were used to identify the blood pool of the Fontan in each slice of the angiogram, allowing for the creation of a 3D Fontan model them exported using the stereolithography (STL) file format. This STL file was hollowed and smoothed. Following, retrospectively-gated, through plane phase-encoded velocity maps were acquired across the IVC, SVC, LPA, and RPA using standard sequences, reconstructing 30 phases per cardiac cycle with a velocity encoding threshold of \(150\,\frac{cm}{second}\). The time-averaged IVC and SVC flow rates were derived from the phase velocity data and prescribed as inlet boundary conditions to the CFD simulations. The time-averaged RPA and LPA flow rates were prescribed as outlet flow splits (the ratio of LPA to RPA). All patient data was collected with the Institutional Review Board approval.
2.2 Geometry Preparation
All models were modified by a “Deform” function which globally smooth out the models’ surfaces, reducing irregular surfaces, using Meshmixer (Autodesk Inc., San Rafael, CA). Deformation of the original model from smoothing was minimized by applying “Shape Preserving” method. Since the smoothed models were extremely fine meshed and caused some software to crash, the mesh size was reduced by 50%, leaving us with around 30,000 triangles per model. Then, 50 mm long extensions were added at the each end of the boundaries for two important purposes. The inlet extensions enabled the velocity profiles to fully develop before the blood enters the computationally interesting areas. The outlet extensions allowed the numerical flow data to stabilize and provide more accurate results [13, 15]. The boundary cuts were adjusted in CAD (SolidWorks, Dasault, France) to ensure smooth extensions of the boundaries. The final model was converted into the text-based Parasolid file and showed improved cell qualities including aspect ratio, maximum skewness, and minimum orthogonal values (Table 1), the deterministic features for the numerical computation accuracy and stability [4].
2.3 CFD Simulation
Performance Metric. The blood flow inside the Fontan graft was virtually simulated through CFD (ANSYS, Pennsylvania, USA) to determine its performance by the indexed power loss (iPL), hepatic flow distribution (HFD), and the non-physiological wall shear stress percentage (%WSS). iPL, a deterministic factor of the abrupt blood flow changes causing cardiac performance impairment [1], was calculated using the Eq. 1, derived from power loss (Eq. 2):
where p being the static pressure, \(\rho \) the density, A the boundary area, v the velocity, \(Q_s\) the systemic venous flow, and the BSA the body surface area [7]. Unbalanced HFD overstresses the heart and progresses malformation of pulmonary arteriovenous [14]. HFD was estimated by computing the ratio of the number of particles passed through each outlets from the IVC. The particles at the IVC was evenly spaced with a 0.1 mm marker size and 1 mm spacing factor setting. The percentage of Fontan and outlet areas falling below \(1\,\frac{dynes}{cm^2}\) in WSS were estimated since the low WSS represents the low-flow in venous stasis causing deposition of procoagulant [8]. In summary, Fontan models with iPL lower than 0.03, HFD between 40:60 or 60:40, and %WSS below 10% were considered to have healthy hemodynamic performance.
Meshing. Mesh size was tested to bolster the computation accuracy and time efficiency. The meshing could either be uniform where the elements are roughly the same size or non-uniform with a max element size defined. Our test runs confirmed that the CFD results between uniform and non-uniform were similar, but non-uniform meshing performed much faster (see Table 2). Following, the max element sizes, between 0.7 mm to 1.5 mm, were tested to identify the best size for creating mesh around the sharp corners and minimize numerical errors (Table 3). The recommended minimum orthogonal quality is 0.01, and only the 0.7 mm max mesh size was able to get sufficing values. Also considering that the lowest aspect ratio and lowest max skewness was with 0.7 mm, a max element size of 0.7 mm was selected for non-uniform meshing.
Wall Layer. The number of wall layers was explored to obtain accurate WSS measurements. Considering previously reported wall layer values, [3, 12], the range of three to six was tested. These variations had minimal impact on the Fontan hemodynamics and the computing time (Table 4). Thus, the study concluded to use five layers, which is the default setting in ANSYS.
Solver. We compared the pressure-based segregated algorithms including simple, coupled, and PISO. Despite the PISO and coupled algorithms known to be computationally heavy but more accurate, results were close to that of simple algorithm (Table 5). Hence, simple solver was applied to solve the laminar flow, which was confirmed by the Reynolds number. The simulated blood was assumed to be a Newtonian fluid with \(1060\,\frac{kg}{m3}\) density and \(3.71\,mPas\) viscosity [13]. Our CFD simulation used the 3D unsteady Navier-Stokes equations with 40 iterations with each iteration timestep lasting 0.001 s. The x, y, z-velocity and mass conservation residual convergence values were set to \(10^{-5}\) [13].
2.4 Design Optimization
Fontan grafts were optimized by three consecutive iterations of design modifications based on the patient’s anatomy and the performance metric results (Fig. 2). The first iteration included identifying possible paths and anastomoses regions with the assistance of experienced cardiologists. The possible paths avoided colliding with the surrounding anatomy, including heart, major vessels, and spine. Then, the surgically adequate tube-shaped and the y-shaped (bifurcated) Fontan grafts were designed. For a tube-shaped graft, a 3D spline was drawn between 2 points. The starting point was placed at the center of the IVC and the end point was chosen at the center of an ellipse drawn on the identified anatomoses region at the SVC. The IVC’s outline and the ellipse on the SVC with the 3D spline as the centerline were selected for 3D lofting. For easier spline control, 1 or 2 extra points along the intended spline path were added. The bifurcated graft was made with two ellipses on the SVC and connecting it with the IVC using the 2D surface loft function in CAD. Manipulating the curvature of the graft was accomplished by adding an ellipse in between the SVC and IVC, similar to adding 1 or 2 spline points for a tube-shaped graft. The bifurcated Fontan grafts were not always feasible if the identified path was too narrow for two ellipses to be connected. The second iteration involved changing the geometrical parameters of the prior designs considering the hemodynamic performance. The entry angle and the center curve of the Fontans were adjusted when the iPL was higher than 0.03. The location, dimensions, and angles of the ellipse on the anastomoses region acted as the manipulator tool of the direction and the amount of the inlet flow heading to Glenn, adjusting the HFD. High %WSS was controlled by reducing the girth of the Fontans. The significance of each geometrical parameter on the hemodynamic performance was summarized and applied for making slight adjustments to further improve Fontan performance during the third iteration. The Fontan grafts were optimized to achieve the lowest iPL, while maintaining below 10% for %WSS and between 40:60 and 60:40 HFD.
3 Result
The Fontan grafts were optimized hemodynamically for each patient (Fig. 2) using our approach. The optimized Fontan designs had significant improvements on hemodynamics with 40% decrease in iPL for patient one (P1) with a y-shaped graft and 45% increase in flow distribution to the LPA and 61% reduction in %WSS for the second patient (P2) with a tube-like graft.
4 Discussion and Conclusion
We developed 3 benchmark parameters that were based off Haggerty et al.’s larger CFD cohort simulation of 100 patients [7]. This ensured providing patient-specific designs in the hemodynamic optimal when compared to other Fontan patients. %WSS is completely a novel parameter, but is based on relevant clinical data [8] and should be incorporated in all Fontan simulations moving forward. Of note, our method creates a tradeoff between iPL and risk of thrombosis, as larger Fontan grafts will have less power loss but increased risk of thrombosis. This is clinically appropriate given the risk of thrombosis in patients with Fontans [2].
Reducing computational time whilst maintaining accuracy allows more time for feedback from the surgeon and the design team before the Fontan operation. Inevitable, some adjustments are needed in the initial proposed designs, and shorter computational time allows for more design iterations. Our decisions on CFD simulations were made to balance the accuracy and computational time. Rigid wall was assumed in the current CFD simulations. However, fluid-structure interaction is known to provide higher accuracy in WSS calculation [10] and should be implemented in future studies.
This study introduces the unique virtual simulation workflow and computational fluid dynamics for optimizing the Fontan graft design. The re-designed Fontan grafts of two patients using this approach showed significant improvements in hemodynamic parameters (i.e. iPL, HFD, and %WSS). We believe that our unique integration of surgical design and flow simulation has the potential to enable cardiac surgeons to effectively simulate patient specific designs for the Fontan operation, potentially improving the surgical outcomes of patients with complex CHD. Future studies will entail applying this approach on more patient models and manufacturing the designs for implantation.
References
Ascuitto, R.J., Kydon, D.W., Ross-Ascuitto, N.T.: Pressure loss from flow energy dissipation: relevance to Fontan-type modifications. Pediatr. Cardiol. 22(2), 110–115 (2001)
Atz, A.M., et al.: Longitudinal outcomes of patients with single ventricle after the Fontan procedure. J. Am. Coll. Cardiol. 69(22), 2735–2744 (2017)
Biglino, G., et al.: Using 4D cardiovascular magnetic resonance imaging to validate computational fluid dynamics: a case study. Front. Pediatr. 3, 107 (2015)
Diskin, B., Thomas, J.: Effects of mesh regularity on accuracy of finite-volume schemes. In: 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Aerospace Sciences Meetings (2012)
Fukunishi, T., et al.: Preclinical study of patient-specific cell-free nanofiber tissue-engineered vascular grafts using 3-dimensional printing in a sheep model. J. Thorac. Cardiovasc. Surg. 153(4), 924–932 (2017)
Gewillig, M.: The fontan circulation. Heart 91(6), 839–846 (2005)
Haggerty, C.M., et al.: Fontan hemodynamics from 100 patient-specific cardiac magnetic resonance studies: a computational fluid dynamics analysis. J Thorac. Cardiovasc. Surg. 148(4), 1481–1489 (2014)
Hathcock, J.J.: Flow effects on coagulation and thrombosis. Arterioscler. Thromb. Vasc. Biol. 26(8), 1729–1737 (2006)
Hoffman, J.I.E., Kaplan, S.: The incidence of congenital heart disease. J. Am. Coll. Cardiol. 39(12), 1890–1900 (2002)
Long, C.C., Hsu, M.C., Bazilevs, Y., Feinstein, J.A., Marsden, A.L.: Fluid-structure interaction simulations of the fontan procedure using variable wall properties. Int. J. Numer. Methods Biomed. Eng. 28(5), 513–527 (2012)
Marsden, A.L., et al.: Evaluation of a novel Y-shaped extracardiac Fontan baffle using computational fluid dynamics. J. Thorac. Cardiovasc. Surg. 137(2), 394–403.e2 (2009)
Ni, M.W., et al.: Computational investigation of a self-powered Fontan circulation. Cardiovasc. Eng. Technol. 9(2), 202–216 (2018)
Siallagan, D., et al.: Virtual surgical planning, flow simulation, and 3-dimensional electrospinning of patient-specific grafts to optimize Fontan hemodynamics. J. Thorac. Cardiovasc. Surg. 155(4), 1734–1742 (2018)
Trusty, P.M., et al.: The first cohort of prospective Fontan surgical planning patients with follow-up data: how accurate is surgical planning? J. Thorac. Cardiovasc. Surg. 157(3), 1146–1155 (2019)
Wei, Z.A., et al.: Can time-averaged flow boundary conditions be used to meet the clinical timeline for Fontan surgical planning? J. Biomech. 50, 172–179 (2017)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Kim, B. et al. (2019). Virtual Cardiac Surgical Planning Through Hemodynamics Simulation and Design Optimization of Fontan Grafts. In: Shen, D., et al. Medical Image Computing and Computer Assisted Intervention – MICCAI 2019. MICCAI 2019. Lecture Notes in Computer Science(), vol 11768. Springer, Cham. https://doi.org/10.1007/978-3-030-32254-0_23
Download citation
DOI: https://doi.org/10.1007/978-3-030-32254-0_23
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-32253-3
Online ISBN: 978-3-030-32254-0
eBook Packages: Computer ScienceComputer Science (R0)