Abstract
Security monitors have been used to check for safety program properties at runtime, that is for any given execution trace. Such security monitors check a safety temporal property specified by a finite automaton or, equivalently, a regular expression. Checking this safety temporal specification for all possible execution traces, that is the program semantics, is a static analysis problem, more precisely a model checking problem, since model checking specializes in temporal properties. We show that the model checker can be formally designed by calculus, by abstract interpretation of a formal trace semantics of the programming language. The result is a structural sound and complete model checker, which proceeds by induction on the program syntax (as opposed to the more classical approach using computation steps formalized by a transition system). By Rice theorem, further hypotheses or abstractions are needed to get a realistic model checking algorithm.
Supported by NSF Grant CCF-1617717.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
- 2.
A definition of the form \(d(\vec {x})\triangleq \{f(\vec {x}\prime )\mid P(\vec {x}\prime ,\vec {x})\}\) has the variables \(\vec {x}\prime \) in \(P(\vec {x}\prime ,\vec {x})\) bound to those of \(f(\vec {x}\prime )\) whereas \(\vec {x}\) is free in \(P(\vec {x}\prime ,\vec {x})\) since it appears neither in \(f(\vec {x}\prime )\) nor (by assumption) under quantifiers in \(P(\vec {x}\prime ,\vec {x})\). The \(\vec {x}\) of \(P(\vec {x}\prime ,\vec {x})\) is therefore bound to the \(\vec {x}\) of \(d(\vec {x})\).
- 3.
We understand “regular model checking” as checking temporal specifications given by a regular expression. This is different from [1] model checking transition systems which states are regular word or tree languages.
- 4.
By introduction of an auxiliary variable
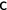 incremented at each program step one can simulate a trace with invariants. But then the reasoning is not on the original program
incremented at each program step one can simulate a trace with invariants. But then the reasoning is not on the original program
 but on a transformed program
but on a transformed program
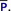 . Invariants in
. Invariants in
 holding for a given value of
holding for a given value of
 of
of
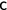 also hold at the position
also hold at the position
 of the traces in
of the traces in
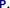 This king of indirect reasoning is usually heavy and painful to maintain when programs are modified since values of counters are no longer the same. The use of temporal specifications has the advantage of avoiding the reasoning on explicit positions in the trace.
This king of indirect reasoning is usually heavy and painful to maintain when programs are modified since values of counters are no longer the same. The use of temporal specifications has the advantage of avoiding the reasoning on explicit positions in the trace.
References
Abdulla, P.A., Jonsson, B., Nilsson, M., Saksena, M.: A survey of regular model checking. In: Gardner, P., Yoshida, N. (eds.) CONCUR 2004. LNCS, vol. 3170, pp. 35–48. Springer, Heidelberg (2004). https://doi.org/10.1007/978-3-540-28644-8_3
Alur, R., Mamouras, K., Ulus, D.: Derivatives of quantitative regular expressions. In: Aceto, L., Bacci, G., Bacci, G., Ingólfsdóttir, A., Legay, A., Mardare, R. (eds.) Models, Algorithms, Logics and Tools. LNCS, vol. 10460, pp. 75–95. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63121-9_4
Ball, T., Levin, V., Rajamani, S.K.: A decade of software model checking with SLAM. Commun. ACM 54(7), 68–76 (2011)
Ball, T., Podelski, A., Rajamani, S.K.: Boolean and cartesian abstraction for model checking C programs. In: Margaria, T., Yi, W. (eds.) TACAS 2001. LNCS, vol. 2031, pp. 268–283. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-45319-9_19
Biere, A., Cimatti, A., Clarke, E.M., Strichman, O., Zhu, Y.: Bounded model checking. Adv. Comput. 58, 117–148 (2003)
Bryant, R.E.: Graph-based algorithms for boolean function manipulation. IEEE Trans. Computers 35(8), 677–691 (1986)
Brzozowski, J.A.: Derivatives of regular expressions. J. ACM 11(4), 481–494 (1964)
Campbell, R.H., Habermann, A.N.: The specification of process synchronization by path expressions. In: Gelenbe, E., Kaiser, C. (eds.) OS 1974. LNCS, vol. 16, pp. 89–102. Springer, Heidelberg (1974). https://doi.org/10.1007/BFb0029355
Clarke, E.M., Emerson, E.A.: Design and synthesis of synchronization skeletons using branching time temporal logic. In: Kozen, D. (ed.) Logic of Programs 1981. LNCS, vol. 131, pp. 52–71. Springer, Heidelberg (1982). https://doi.org/10.1007/BFb0025774
Clarke, E.M., Henzinger, T.A., Veith, H., Bloem, R. (eds.): Handbook of Model Checking. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-10575-8
Clarke, E.M., Klieber, W., Nováček, M., Zuliani, P.: Model checking and the state explosion problem. In: Meyer, B., Nordio, M. (eds.) LASER 2011. LNCS, vol. 7682, pp. 1–30. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-35746-6_1
Cousot, P.: Méthodes itératives de construction et d’approximation de points fixes d’opérateurs monotones sur un treillis, analyse sémantique de programmes (in French). Thèse d’Étatès sciences mathématiques, Université de Grenoble Alpes, Grenoble, France, 21 March 1978
Cousot, P.: Partial completeness of abstract fixpoint checking. In: Choueiry, B.Y., Walsh, T. (eds.) SARA 2000. LNCS (LNAI), vol. 1864, pp. 1–25. Springer, Heidelberg (2000). https://doi.org/10.1007/3-540-44914-0_1
Cousot, P., Cousot, R.: Abstract interpretation: a unified lattice model for static analysis of programs by construction or approximation of fixpoints. In: POPL, pp. 238–252. ACM (1977)
Cousot, P., Cousot, R.: Constructive versions of Tarski’s fixed point theorems. Pac. J. Math. 81(1), 43–57 (1979)
Cousot, P., Cousot, R.: Systematic design of program analysis frameworks. In: POPL, pp. 269–282. ACM Press (1979)
Cousot, P., Cousot, R.: Temporal abstract interpretation. In: POPL, pp. 12–25. ACM (2000)
Crafa, S., Ranzato, F., Tapparo, F.: Saving space in a time efficient simulation algorithm. Fundam. Inform. 108(1–2), 23–42 (2011)
Cyphert, J., Breck, J., Kincaid, Z., Reps, T.: Refinement of path expressions for static analysis. PACMPL 3(POPL), 45 (2019)
Giacobazzi, R., Quintarelli, E.: Incompleteness, counterexamples, and refinements in abstract model-checking. In: Cousot, P. (ed.) SAS 2001. LNCS, vol. 2126, pp. 356–373. Springer, Heidelberg (2001). https://doi.org/10.1007/3-540-47764-0_20
Giacobazzi, R., Ranzato, F.: Incompleteness of states w.r.t. traces in model checking. Inf. Comput. 204(3), 376–407 (2006)
Heizmann, M., Hoenicke, J., Podelski, A.: Software model checking for people who love automata. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 36–52. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-39799-8_2
Hopcroft, J.E., Motwani, R., Ullman, J.D.: Introduction to Automata Theory, Languages, and Computation - International Edition, 2nd edn. Addison-Wesley, Boston (2003)
King, J.C.: Symbolic execution and program testing. Commun. ACM 19(7), 385–394 (1976)
Kleene, S.C.: Representation of events in nerve nets and finite automata. In: Shannon, C.D., McCarthy, J. (eds.) Automata Studies, pp. 3–42. Princeton University Press, Princeton (1951)
Kripke, S.A.: Semantical considerations on modal logic. Acta Philosophica Fennica 16, 83–94 (1963). Proceedings of a Colloquium on Modal and Many-Valued Logics, Helsinki, 23–26 August 1962
Kupferman, O.: Automata theory and model checking. In: Clarke, E., Henzinger, T., Veith, H., Bloem, R. (eds.) Handbook of Model Checking, pp. 107–151. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-10575-8_4
Lichtenstein, O., Pnueli, A.: Checking that finite state concurrent programs satisfy their linear specification. In: POPL, pp. 97–107. ACM Press (1985)
Mallios, Y., Bauer, L., Kaynar, D., Ligatti, J.: Enforcing more with less: formalizing target-aware run-time monitors. In: Jøsang, A., Samarati, P., Petrocchi, M. (eds.) STM 2012. LNCS, vol. 7783, pp. 17–32. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-38004-4_2
Mauborgne, L.: Binary decision graphs. In: Cortesi, A., Filé, G. (eds.) SAS 1999. LNCS, vol. 1694, pp. 101–116. Springer, Heidelberg (1999). https://doi.org/10.1007/3-540-48294-6_7
Miller, S.P., Whalen, M.W., Cofer, D.D.: Software model checking takes off. Commun. ACM 53(2), 58–64 (2010)
Owens, S., Reppy, J.H., Turon, A.: Regular-expression derivatives re-examined. J. Funct. Program. 19(2), 173–190 (2009)
Queille, J.P., Sifakis, J.: Specification and verification of concurrent systems in CESAR. In: Dezani-Ciancaglini, M., Montanari, U. (eds.) Programming 1982. LNCS, vol. 137, pp. 337–351. Springer, Heidelberg (1982). https://doi.org/10.1007/3-540-11494-7_22
Sakarovitch, J.: Elements of Automata Theory. Cambridge University Press, Cambridge (2009)
Schneider, F.B.: Enforceable security policies. ACM Trans. Inf. Syst. Secur. 3(1), 30–50 (2000)
Wolper, P.: Temporal logic can be more expressive. Inf. Control 56(1/2), 72–99 (1983)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Cousot, P. (2019). Calculational Design of a Regular Model Checker by Abstract Interpretation. In: Hierons, R., Mosbah, M. (eds) Theoretical Aspects of Computing – ICTAC 2019. ICTAC 2019. Lecture Notes in Computer Science(), vol 11884. Springer, Cham. https://doi.org/10.1007/978-3-030-32505-3_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-32505-3_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-32504-6
Online ISBN: 978-3-030-32505-3
eBook Packages: Computer ScienceComputer Science (R0)





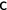 incremented at each program step one can simulate a trace with invariants. But then the reasoning is not on the original program
incremented at each program step one can simulate a trace with invariants. But then the reasoning is not on the original program
 but on a transformed program
but on a transformed program
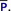 . Invariants in
. Invariants in
 holding for a given value of
holding for a given value of
 of
of
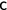 also hold at the position
also hold at the position
 of the traces in
of the traces in
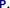 This king of indirect reasoning is usually heavy and painful to maintain when programs are modified since values of counters are no longer the same. The use of temporal specifications has the advantage of avoiding the reasoning on explicit positions in the trace.
This king of indirect reasoning is usually heavy and painful to maintain when programs are modified since values of counters are no longer the same. The use of temporal specifications has the advantage of avoiding the reasoning on explicit positions in the trace.