Keywords

1 Introduction

Fluorescein Fundus Angiography (FFA) is widely used for imaging the functional state of retinal circulation [13]. With angiographic imaging, detailed information of human retina fundus are enhanced and augmented including vessels and granular structures, which make it a routine diagnostic tool for disease diagnosis including choroiditis, preretinal hemorrhage and diabetic retinopathy [1, 14]. However, it is an image modality that both doctors and patients are reluctant to use. Invasive operation, harmful fluorescein dye, consequent side effects and potential complications force physicians only use it in severe situations [10].

Moreover, conventional Fluorescein Fundus (FF) imaging is non-invasive and safe. It is a widely used technique for early diagnosis and regular checkup in hospitals. Since the common retina structures like vessels and granular structures are shared in both domains, we propose an approach to use non-invasive and safe FF images to synthesize the invasive and harmful FFA images. Synthesizing FFA images could help doctors to diagnosis with smaller potential risk in patients and relatively reduce the need for actual angiographic imaging.

Medical image synthesis and translation between different domains has been well studied in the past several years. Considering large radiation explosion of CT, Nie et al. [11, 12] proposed a context-aware generative adversarial network to synthesize CT images from MRI images. However, their methods need paired data, which are hard to obtain in practice. Chartsias et al. [2] presented an approach based on latent representation, which aims to synthesize multi-output images with multi-input MRI brain images. Similarly, their methods also required aligned image pairs as input. Moreover, their methods focused more about the discovery of modality-invariant content features and ignore the modality-specific features. As image pairs from two image domains of the same patient with the same disease are relatively rare and creates higher demands for data acquisition, the proposed image synthesis method is based on unpaired data in an unsupervised way.

There are also several image synthesis works focused on retina fundus images. Zhao et al. [16, 17] and Costa et al. [3] synthesized retina fundus images based on the corresponding segmentation masks for the purpose of data augmentation, segmentation and other usages. These approaches also required fundus images and the corresponding masks to construct training pairs, which similarly also cause difficulty for data acquisition.

Hervella et al. [5] and Schiffers et al. [13] share a similar motivation with us. They also developed approaches to generate FFA images based on retina fundus images. Similar to previous methods, Hervella et al. [5] constructed a Unet architecture with fundus images as input and FFA images as output to learn a direct mapping between two domains. Without the help of adversarial learning, their method leads the model to learn a pixel-to-pixel mapping instead of distribution-to-distribution mapping. Due to the scarcity of paired data, the model would easily become overfitting, which deteriorates the generalization ability of the model.

Schiffers et al. [13] handled this problem with the unpaired data. Inspired by CycleGAN [18], their approach adopted the cycle consistency loss to add reverse mapping for the image translation from FF domain to FFA domain. However, CycleGAN-based methods use two separate generators to learn the translation between two domains, which ignores the implicit relationship of feature translation during the image synthesis process. To be more specific, during translation, structure features are shared in both domains including vessels and granular structure. On the contrary, appearance features are distinctive between two domains like color. As CycleGAN [18] does not utilize these information, the translation process is less controllable.

To solve that, we proposed an unsupervised image synthesis method via disentangled representation learning based on unpaired data. Our approach is based on an assumption that images from two domains could be mapped to the same latent representation in a shared space [8, 9]. Inspired by that, we use three encoders to disentangle the domain features into domain-shared structure features and domain-independent appearance features. After that, FFA appearance features are fused with domain-shared structure features to synthesize the required FFA-like images by FFA domain generator. We also put domain-shared structure features into FF domain generator to help stabilize the training process. By adversarial learning, two generators are pushed to synthesize FFA-like images and FF-like images respectively. Moreover, we apply perceptual loss to preserve the structural information during translation. The proposed method is evaluated on public Isfahan MISP dataset [4] with other state-of-the-art methods. Qualitative analysis shows that our methods could generate mimic FFA images. Meanwhile the quantitative comparison demonstrates our method could produce synthetic images with superior image quality over other methods.

2 Methodology

Our method aims to learn a image distribution mapping from domain FF to domain FFA without paired data. To be more specific, for any synthetic FFA image, it should have the structure of the FF image it generates from, combined with the appearance of domain FFA. In the following section, we introduce the disentanglement of domain-shared structure features and domain-independent appearance features first. After that, we describe perceptual loss to make sure the structure-consistency during image translation process. We also introduced other important loss including KL loss and adversarial loss in the end of this section.

2.1 Disentanglement of Structure Features and Appearance Features

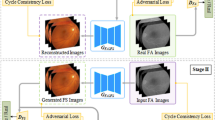
There exist common structures like vessels and granular structures between domain FF and domain FFA. Intuitively we use two structure encoders to extract the common features that are shared in two domains \(\left\{ E_{FF}^{S}, E_{{FFA}}^{S}\right\} \). Meanwhile, we use one appearance encoder \(E_{FFA}^{A}\) to capture the independent FFA attributes. Besides that, we also adopt generators \(\left\{ G_{FF}, G_{FFA}\right\} \) and discriminators \(\left\{ D_{FF}, D_{FFA}\right\} \) for two domains, as shown in Fig. 1.

To better deal with non-corresponding data, there are two stages in our model. The forward translation stage learns a mapping from real images to generated images as follows:

$$\begin{aligned} fake\_FFA&=G_{FFA}\left( E_{FFA}^{A}(I_{FFA}), E_{FF}^{S}(I_{FF})\right) , \end{aligned}$$
(1)
$$\begin{aligned} fake\_FF&=G_{FF}\left( E_{FFA}^{S}(I_{FFA})\right) . \end{aligned}$$
(2)

Beside that, in backward translation stage, we add a reverse mapping from the generated images back to real images [18], which is formulated as:

$$\begin{aligned} \hat{I_{FFA}}&=G_{FFA}\left( E_{FFA}^{A}\left( fake\_FFA\right) , E_{FF}^{S}\left( fake\_FF\right) \right) , \end{aligned}$$
(3)
$$\begin{aligned} \hat{I_{FF}}&=G_{FF}\left( E_{FFA}^{S}\left( fake\_FFA\right) \right) . \end{aligned}$$
(4)
Fig. 1.
figure 1

Model Architecture, where the green and blue blocks represent for structure encoders and appearance encoders. Yellow blocks stand for generators and discriminators. Green dotted lines stand for shared weights between structure encoders. (Color figure online)

Full size image

To achieve better representation disentanglement, we apply weight sharing strategy and perceptual loss. For the weight sharing strategy, We let the last layer of \(E_{FF}^{S}\) and \(E_{FFA}^{S}\) to share weights based on the assumption that two domains share one latent content space [9]. The weight sharing strategy could effectively map the domain-shared structure information between two domains into the same latent space.

Moreover, to make sure the generated FFA images could preserve as much as content features of FF images, we construct a perceptual loss between the real FF images and fake FFA images by using the features of a well-trained network. Since a well-trained model contains rich high-level semantic features, it implies that if the real images and generated images have the same structure information, after feeding them into a pre-trained model, they should produce similar high-level features [6, 15]. Therefore, the distance of the features above could be act as an evaluation metric of content similarity. Based on that, we construct a perceptual loss to preserve structure-consistency as:

$$\begin{aligned} \mathcal {L}_{p}=\left\| \phi _{l}\left( I_{FFA}\right) -\phi _{l}(fake\_FFA)\right\| _{2}^{2}, \end{aligned}$$
(5)

where \(\phi _{l}(x)\) represents for the con3, 3 layer in VGG-19 network [6].

2.2 Loss Functions

Cycle-Consistency Loss. Since there is no paired data involved in the image translation process, we constrain the image translation process by forcing the generated images could be translated back into real images and add L1 loss between the constructed images and input images. The cycle-consistency loss of two domains is defined as:

$$\begin{aligned} \mathcal {L}_{c c}=\mathbb {E}_{FF \sim p(FF)}\left[ \Vert I_{FF}-\hat{I_{FF}}\Vert _{1}\right] +\mathbb {E}_{FFA \sim p(FFA)}\left[ \Vert I_{FFA}-\hat{I_{FFA}}\Vert _{1}\right] . \end{aligned}$$
(6)

KL Loss. Since the encoder-generator architecture is basically a Variation Auto-encoder (VAE), we introduce the KL divergence loss in appearance feature extraction. KL loss forces the appearance representation \(z_{FFA}=E_{FFA}^A(I_{FFA})\) to be close to the normal Gaussian distribution \(p(z) \sim N(0,1)\), which would help suppress the structure information contained in \(z_{FFA}\). The KL loss is defined as:

$$\begin{aligned} K L\left( q\left( z_{FFA}\right) \Vert p(z)\right) =-\int q\left( z_{FFA}\right) \log \frac{p(z)}{q\left( z_{FFA}\right) } d z. \end{aligned}$$
(7)

In VAE, minimizing KL loss is equivalent to minimizing the following equation [7]:

$$\begin{aligned} \mathcal {L}_{K L}=\frac{1}{2} \sum _{i=1}^{N}\left( \mu _{i}^{2}+\sigma _{i}^{2}-\log \left( \sigma _{i}^{2}\right) -1\right) , \end{aligned}$$
(8)

where \(\mu \) and \(\sigma \) are the mean and standard deviation of appearance feature \(z_{FFA}\). And \(z_{FFA}\) is sampled as \(z_{FFA}=\mu + z\circ \sigma \), where \(\circ \) is the element-wise multiplication.

Adversarial Loss. To generate more realistic and mimic images, we impose domain adversarial loss. The adversarial loss of two domains are formulated as:

$$\begin{aligned} \begin{aligned} \mathcal {L}_{D_{FFA}}&= \mathbb {E}_{FFA \sim p(FFA)}\left[ \log D_{FFA}(I_{FFA})\right] +\\&\mathbb {E}_{FF \sim p(FF)}\left[ \log \left( 1-D_{FFA}\left( G_{FFA}\left( E_{FF}^{S}(I_{FF}), E_{FFA}^A(I_{FF})\right) \right) \right) \right] , \end{aligned} \end{aligned}$$
(9)
$$\begin{aligned} \begin{aligned} \mathcal {L}_{D_{FF}}&= \mathbb {E}_{FF \sim p(FF)}\left[ \log D_{FF}(I_{FF})\right] +\\&\mathbb {E}_{FFA \sim p(FFA)}\left[ \log \left( 1-D_{FF}\left( G_{FF}\left( E_{FFA}^{S}(I_{FFA})\right) \right) \right) \right] . \end{aligned} \end{aligned}$$
(10)

The generator tries to generate mimic fake images to fool the discriminator, while the discriminator tries to distinguish between the real images and fake images.

The full objective function is formed by the weighted sum of perceptual loss, KL loss, cycle-consistency loss and adversarial loss as follows:

$$\begin{aligned} \mathcal {L}=\lambda _{a d v} \mathcal {L}_{a d v}+\lambda _{K L} \mathcal {L}_{K L}+\lambda _{c c} \mathcal {L}_{c c}+\lambda _{p} \mathcal {L}_{p}, \end{aligned}$$
(11)

where \(\mathcal {L}_{a d v}=\mathcal {L}_{D_{FFA}}+\mathcal {L}_{D_{FF}}\) and the hyper-parameters are setting empirically. In testing, there still needs one FFA image as appearance guide image. According to our observation, the FFA images have minor appearance differences and the choice of guide images has little influence to the generated images, which will be demonstrated in detail at the end of next section.

3 Experiments and Results

3.1 Dataset

In experiments, we use Isfahan MISP dataset which contains 59 image pairs in total [4]. In specific, 30 pairs are healthy cases and 29 pairs are abnormal cases with diabetic retinopathy. We randomly pick 29 pairs as the training set and leave the remaining 30 pairs as the test set. It is worth to mention that the images fed into our methods and Schiffers et al. [13] are randomly chosen and randomly cut into patches to make sure no pair information is involved during the training. Also, since our methods needs a FFA image as appearance guide image in testing, the guide image is also randomly picked. The choice of guide images has very little influence to the final results, which will be demonstrated in the end of this section.

3.2 Technique Details

In order to extract more details, we cut the whole images with the resolution of \(720\times 576\) into \(256\times 256\) patches and perform data augmentation including rotation, random crop and random flip. The structure encoder \(E_{FFA}^S\) and \(E_{FF}^S\) consist of 3 convolution layers and 4 residual blocks where the last residual block shares weights with each other. For the appearance encoder \(E_{FFA}^A\), we use four convolution layers and one fully connected layer in the end. The generator \(G_{FFA}\) and \(G_{FF}\) have a symmetric architecture to the structure encoder, which are constructed by 4 residual blocks and 3 transposed convolution layers. In the training process, Adam optimizer is used to update discriminator first and generator and encoder later with beta1 and beta2 setting to 0.5 and 0.999 respectively. The initial learning rate is set to be 0.0001 for the first 50 epochs and linearly decayed for the following 50 epochs. During training, the hyper-parameters \(\lambda _{adv}\), \(\lambda _{cc}\), \(\lambda _{KL}\) and \(\lambda _{pp}\) set to be 1, 10, 0.01 and 0.001 respectively. The entire training requires around 6 h computed with one NVIDIA TITAN V GPU card.

Fig. 2.
figure 2

Qualitative results of our methods and compared methods.

Full size image
Fig. 3.
figure 3

Enlarged details of synthetic images generated by our methods and other compared methods, where the first row and second row represent for the original size of synthetic images and the zoom-in details of the red bounding box respectively. The arrows with the same color point out the tiny vessels in the same region. (Color figure online)

Full size image

3.3 Qualitative Analysis

We compare our results with Hervella et al. [5] and Schiffers et al. [13], which tackle the same task with us. We visualize several synthetic images generated by the comparison methods and our methods in Fig. 2. All three methods could capture main vessel structures in real FF images. However, the results of Hervella et al. [5] have low contrast between the vessels and other tissues. The detailed vessels in the center blend into the surroundings which causes difficulty to observe. Schiffer et al. [13] produces better image contrast and highlights the vessels. However, direct mapping between two domains without structure consistency constrain makes the model lack the ability to preserve tiny details like small vessels in the center, which are enlarged and illustrated in Fig. 3 for better image contrast. On the other side, our results preserve the basic vessel structure with clear edges and keep the detailed vessels as well. Moreover, our results have similar appearance to real FFA images.

3.4 Quantitative Analysis

For quantitative comparison, we use several standard evaluation metrics including Peak signal-to-noise Ratio (PSNR), Mean Squared Error (MSE) and Structural Similarity Index (SSIM) to evaluate the image quality of generated images, as shown in Table 1. Due to the size of training dataset, the method of Hervella et al. [5] based on paired data are easy to overfit. Their results are not as good as that of Schiffers et al. [13], which utilizes the unpaired images to better exploit feature representation in limited data. The method of Schiffers et al. [13] obtains better results in MSE, PSNR and SSIM by 0.0775, 4.7675 and 0.0222 respectively. Meanwhile, as our method takes advantage of domain-shared structure features and domain-independent appearance features in the synthesis process while the approach of Schiffers et al. [13] ignores the implicit feature relationship, our results achieve \(2.19\%\) and \(0.014\%\) improvements in PSNR and SSIM compared to Schiffers et al. [13]. The MSE of our results is also lower than that of Schiffers et al. [13] by \(0.0164\%\), which demonstrates the effectiveness of our methods and shows the generated images could well preserve structures in FF images.

Since our method needs a FFA image as the appearance guide image to generate mimic FFA images in testing, we also explore the influence of different guide images to the final synthetic images. In this experiment, all FFA images in training dataset are tested here. We compare the standard deviation (std) of MSE, PSNR and SSIM of our synthetic results under different guide images, which are shown in Table 2.

As shown in Table 2, the std of MSE, PSNR and SSIM are relatively small, which implies the image quality of fake FFA images guided by different FFA images have little fluctuation. It also demonstrates that the choice of guide images has minor effects to the generated images.

Table 1. Comparison with other methods in test data.
Full size table
Table 2. Quantitative results of different guide images.
Full size table

4 Discussion and Conclusion

Due to the invasive operation and harmful fluorescein dye of Fluorescein Fundus Angiography, we proposed an image synthesis method based on disentangled representation learning to synthesize mimic FFA images from non-invasive and safe Fluorescein Fundus images. Considering data acquisition, the proposed method is designed for unpaired data in unsupervised way. The features of two domains are disentangled into domain-shared structure features and domain-independent appearance features. By adversarial learning, two domain discriminators push generators to synthesize realistic images. To preserve content features during translation, perceptual loss is applied. Both the quantitative comparison and qualitative analysis demonstrate that our methods could generate competitive mimic results with good image quality compared with the state-of-the-art methods.