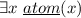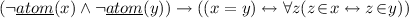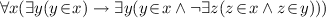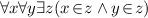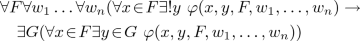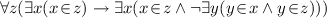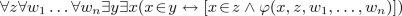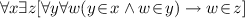Mathematical Foundation of Cognitive Computing Based Artificial Intelligence

Abstract

Today Cognitive computing and Artificial Intelligence (AI) face the same challenges namely, simulate human thought processes and mimic the way human brain works. The main difference between Cognitive computing and AI is: (i) AI models various functions of human intelligence, where computer is one of the modelling means though often the most important one, i.e. intelligence is in the focus while (ii) Cognitive computing models human thought processes and simulates the hypothetical way human brain works as computation.

Our aim is to develop a theoretically and methodologically well-founded theory of AI together with a unified computational theory, which will provide specific tools and methods for Cognitive computing.

To achieve our goal we follow a methodology triangle, consisting of a conceptual-philosophical, a system theoretical and a logical-mathematical component. Computing will play a fundamental role in both system-theoretical and logical-mathematical methodological components.

Hereby we concentrate on the development of the logical-mathematical foundation in detail by the use of category theory, which provides an excellent frame for defining all notions necessary for developing a universal theory for computing, specification, cognitive reasoning, information, knowledge and their various combinations. Foundation theory is by the use of the so-called constitutions, the mathematical basis for the cognitive computation. Logical foundation will be developed as a special constitution and cognitive computing processes are defined by using situations, infons and information. The main properties are discussed with some examples.

7 Appendixes

1.1 7.1 Axiomatization of $clFSA$

In order to interpret program execution and different data and control structures, our theory of programming needs appropriate models to be obtained from a relation structure (models) of a given similarity type by building up the corresponding superstructure as we have seen so far. However, to use these superstructures in our theory of programming we have to introduce an appropriate formalism which allows to provide a theory (an axiomatization) the models of which are the structures in question and by the use of which, statements can be formulated and proved about these structures. According to our aim to develop a first order theory of programming the axiomatization of superstructures will be done in an appropriate first order language.

Superstructure construction is followed by a set–theoretic approach so the signature of the language has to contain at least:

• a unary relation symbol $\underline{atom}: d$

to distinguish the elements of the original relation structure from which the superstructure is built up. These elements may be considered as elementary data;

• the ‘element’ relation symbol $\in :d,d$

• and the constant symbol $0:\rightarrow d$

which reflects the empty set.

A similarity type $\sigma$ is called rich enough iff it contains the above symbols. We use $\notin$ for the negation of element relation.

The variable symbols of the language correspond to sets and atoms. Therefore, sets and their elements are of the same nature, if the latter ones are not atoms. In other words, we consider hereditary sets the elements of which are either atoms or hereditary sets etc. Though atoms have no elements they are not equivalent to the empty set. Therefore we have to be careful while providing the Axiom of Extensionality and defining some of the set-theoretic operations.

A relation symbol of $\sigma$ is called non set-theoretical iff it is not equal with either $\in$ or 0 or to $\underline{atom}$.

The system of axioms $FSA_\sigma$ axiomatizes the hereditarily finite sets with atoms. Why do we need atoms? As we know the Zermalo-Fraenkel axiomatization is powerful enough to make atoms unnecessary. Set theory, as formalized in ZFC, provides an elegant and powerful way to organize mathematics but it is too strong for the programming theory. The aim to build up an adequate axiom system for this theory dictates to develop a set theory weaker than ZFC, weak in the principles of set existence which they attempt to formalize e.g. by allowing atoms. The latters just have a programming interpretation as elementary data or, if you think about the relation structures as the object modelling computers where the programs run then atoms represent the registers where the data are stored. Atoms also break the finiteness which we intend to axiomatize since they may be infinitely many. We axiomatize the hereditarily finite sets with atoms by modifying the axiom system ZF as follows:

• $FSA_0$: Existential axiom of atoms:

  

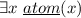
• $FSA_1$: Extensionality axiom:

  

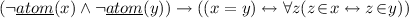
• $FSA_2$: Empty set axiom:

  

• $FSA_3$: Significance axiom of atoms:

  

This axiom together with $FSA_1$ declares that though atoms have no elements they differ from the empty set 0.

• $FSA_4$: Foundation axiom:

  

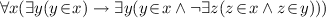
This axiom says that every non-empty set has a minimal element with respect to $\in$.

• $FSA_{5\sigma }$: Comprehension Scheme. For each $\sigma$-type formula $\varphi$:

  

The y asserted to exist is unique by Extensionality Axiom and it is denoted by

$$\begin{aligned} \{x|x\!\in \!z\wedge \varphi (x,y,w_1,\ldots ,w_n)\}\ \mathrm{or\ }\{x\!\in \!z|\varphi \}. \end{aligned}$$

Intuitively for a given formula $\varphi (x)$ there need not necessarily exist a set $\{x:\varphi (x)\}$ this collection may be too large to form a set. However, Comprehension Scheme says that if the collection is a subcollection of a given set then it does exist. The following axioms say that certain sets, which should exist, really do exist.

• $FSA_6$: Pairing axiom:

  

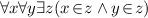
• $FSA_7$: Union axiom:

  

• $FSA_{8\sigma }$: Replacement scheme. For each $\sigma$-type formula $\varphi$:

  

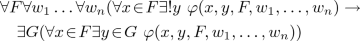
Intuitively (using also $FSA_{5\sigma }$) this axiom says that if H(x) is the unique y satisfying $\varphi (x,y,\ldots )$ then $\{H(x)|x\!\in \!F\}$ is a set.

• $FSA_9$: Finiteness axiom:

  

Definition 23

The set of axioms of the hereditarily finite sets with atoms is:

$$\begin{aligned} FSA_\sigma \leftrightharpoons \{FSA_i|i=0,1,2,3,4,6,7,9\}\cup \{FSA_{i\varphi }|i=5,8, \ \varphi \!\in \!Form_\sigma \}. \end{aligned}$$

If $R_1,\ldots ,R_k;f_1,\ldots ,f_n$ are new relation and function symbols respectively then $FSA_\sigma (R_1,\ldots ,R_k;f_1,\ldots ,f_n)$ stands for $FSA_{\sigma ^*}$ where $\sigma ^* = \sigma \cup (R_1,\ldots ,R_k;f_1,\ldots ,f_n)$.

The Finiteness Axiom implies the Axiom of Choice, i.e.:

Proposition 4

In $FSA_\sigma$ the following statements hold:

• (i) Each set can be well-ordered.

• (ii) There exists a choice function on sets.

Moreover, basically from the Finiteness Axiom, it follows that for any set there exists the power set, i.e. the Power Set Axiom is a consequence of $FSA_\sigma$.

Proposition 5

The axioms of $FSA_\sigma$ ensure that for any set there exists the power set:

$$\begin{aligned} FSA_\sigma \models \forall x(\lnot \underline{atom}(x)\rightarrow \exists y\forall z(z\!\in \!y\leftrightarrow z\subset x)). \end{aligned}$$

Therefore, the axiom system $FSA_\sigma$ is equivalent with the Zermalo-Fraenkel axiom system with the Axiom of Infinity and the Power Set Axiom deleted and Finiteness Axiom added.

Note that all the notions introduced in ZFC can be introduced in $FSA_\sigma$ as well. E.g. relation, domain, range, function, bijection, surjection, injection are such notions. The expressions that define these notions can also be used as a definition of new relation or function symbols. Adding these new symbols to the similarity type o and their definitions to $FSA_\sigma$, we obtain a conservative extention of $FSA_\sigma$.

Since in $FSA_\sigma$ all sets are finite, therefore the following preposition holds for ordinals:

Proposition 6

Each ordinal is finite in $FSA_\sigma$ and the usual addition and multiplication on ordinals are commutative.

Note that in set theory natural numbers are identified with finite ordinals. Namely, an ordinal $\alpha$ is a natural number if for all $\beta \le \alpha$ if $\beta \ne 0$ then $\beta$ is a successor of some $\gamma$. Again the Finiteness Axiom implies the following:

Proposition 7

The natural numbers, the ordinals (and the cardinals) are the same in $FSA_\sigma$.

A programming theory needs, among others, tools to handle infinite objects e.g. to represent infinite computation processes. Therefore, beyond finite sets as finite objects, we also have to be able to speak about infinite objects.

Different approaches provide different techniques for this aim, e.g. denotation approach to semantics makes the topological space complete. We introduce the notion of class to handle infinity. This notion is also important in ZFC axiom system, where e.g. the class of all ordinals On is often used. In the axiom system $FSA_\sigma$ the notion of class has a more important role, since the majority of the usual sets (namely, all infinite sets) cannot be identified with any set in $FSA_\sigma$.

Intuitively, a class is but a conglomerate of elements x which satisfy a given formula $\varphi (x)$. Since each $\sigma$-type model of $FSA_\sigma$ has constructive objects (atoms or finite sets) as elements a class is but a defined or specified conglomerate of these objects. Due to the significant role of classes in our further investigations they will frequently appear and we therefore have to precisely define what type of statements can be stated about classes. The definition is based on the followings. Having a given model a class does not consist of arbitrarily collected elements of the universe, but they may be collected only by the use of a given formula. Therefore, we extend the language such that it may contain statements about classes. Let us first fix an arbitrary set cV of the so called class variable. The intended meaning of a class variable in a model of $FSA_\sigma$ is a conglomerate of objects of the universe.

Let $\sigma$ be a rich similarity type. In order to handle classes we extend the $\sigma$-type classical first order language by adding class terms which provide definable conglomerate of objects of the universe of the models and the class formulas which allow to formulate statements about classes.

Definition 24.

• (a) The set of $\sigma$-type class terms (${\mathbf {cTerm}}_\sigma )$ consists of the terms in the form $\{x|\varphi \}$ where $x\!\in \!V$ and $\varphi \!\in \!cForm_\sigma$.

• (b) The set of $\sigma$-type class formulas (${\mathbf {cForm}}_\sigma$) is the minimal set satisfying the followings:

  • $Atom_\sigma \subset cForm_\sigma$;

  • if $x\!\in \!Term_\sigma$ and $C\!\in \!cV$ then $x\!\in \!C$ belongs to $cForm_\sigma$;

  • if $\varphi ,\psi$ are of $cForm_\sigma$ then $\lnot \varphi$ and $\varphi \wedge \psi$ also belong to $cForm_\sigma$;

  • if $\varphi$ is of $cForm_\sigma$, $x\!\in \!V$ then $\exists v\varphi$ also belong to $cForm_\sigma$.

Now let us see how the semantics of $cForm_\sigma$ can be defined. First of all, we extend the notion of valuation for class variables. A valuation of a class variable is a subset of the universe of the model under consideration.

Definition 25

Let $\mathbf {A}$ be an arbitrary but fixed $\sigma$-type model. A class valuation is a function k such that

• $dom(k)=C\cup cV$;

• $k(x)\!\in \!A$ for any $x\!\in \!V$;

• $k(x)\!\in \!Sb(A)$ for any class variable $x\!\in \!cV$.

As usual let $cVal_{\mathbf {A}}$ denote the family of all class valuations.

Having the valuation we can define the meaning of class terms and class formulas with respect to a given valuation in an arbitrary but fixed model.

Definition 26

Let a model $\mathbf {A}\!\in \!Mod_\sigma$ be given.

• (a) The meaning of a class term $t=\{x|\varphi \}$ in the model $\mathbf {A}$ with respect to k is the following family:

  $$\begin{aligned} t_{\mathbf {A}}\leftrightharpoons \{a|\mathbf {A}\models \varphi [k+(x,a)]\}. \end{aligned}$$

• (b) For any class formula $\varphi \!\in \!cForm_\sigma$ and valuation $k\!\in \!cVal_{\mathbf {A}}$ we define the validity $\varphi$ in $\mathbf {A}$ with respect to k (written as $\mathbf {A}\models \varphi [k]$) by induction on the complexity of $\varphi$:

  • if $\varphi \!\in \!Atom_\sigma$ then the validity is defined as in (i) and (ii) of 1.2.10;

  • if $\varphi \leftrightharpoons \tau \!\in \!C$ then $\mathbf {A}\models (\tau \!\in \!C)[k]$ iff $\tau _{\mathbf {A}}[k]$ is an element of k(C) ;

  • and (iv) are defined as in (iii) of 1.2.10 (i.e as usual).

In order to make the class valuation more transparent the $\sigma$-type models may be extended such that they will contain an entity which refers to classes.

Definition 27

A pair $\mathbf {V}=(\mathbf {A},\underline{Class})$ is called a class extention of $\mathbf {A}$ iff

• $\mathbf {A}$ is a $\sigma$-type model;

• $\underline{Class}\subset Sb(A)$;

• for any class term $t\!\in \!cTerm_\sigma$ and valuation $k\!\in \!cVal_{\mathbf {A}}$ we have $k(cV)\subset \underline{Class}$ implies $t_{\mathbf {A}}[k]\!\in \!\underline{Class}$.

Let $cMod_\sigma$ denote the family of all class extentions of $\sigma$-type models. If $\mathbf {V}\!\in \!cMod_\sigma$ then let $Val_{\mathbf {V}}$ denote those class valuations k for which $k(cV)\subset \underline{Class}$ holds.

Definition 28

Let $\mathbf {V}=(\mathbf {A},\underline{Class})$ be an arbitrary class extention belonging to $cMod_\sigma$. Let $\varphi \!\in \!cForm_\sigma$.

• (i) We say that $\varphi$ is valid in V with respect to a valuation k iff $k\!\in \!Val_{\mathbf {V}}$ and $\mathbf {V}\models \varphi [k]$.

• (ii) The class formula $\varphi$ is valid in $\mathbf {V}$ iff it is valid with respect to all $k\!\in \!Val_{\mathbf {V}}$ i.e.

  $$\begin{aligned} \mathbf {V}\models \varphi \text { iff for all }k\!\in \!Val_{\mathbf {V}},\mathbf {V}\models \varphi [k] \end{aligned}$$

• (iii) A class formula $\varphi$ is said to be valid in a $\sigma$-type model $\mathbf {A}$ iff for all class extention $\mathbf {V}= (\mathbf {A},\underline{Class})$ we have $\mathbf {V}\models \varphi$.

So we have defined the $\sigma$-type class language as a triple

$$\begin{aligned} CL_\sigma \leftrightharpoons (cForm_\sigma ,cMod_\sigma ,\models ) \end{aligned}$$

This language is really a two-sorted one. The first sort corresponds to sets and atoms and the second one to classes. However, quantification is allowed only for set variables.

A variable $x\!\in \!V\cup cV$ can also be considered as a shorthand for the class term $\{y|y\!\in \!x\}$ To have a clearer view of a variable let us see how the “element relation” $\in$ and the equality are defined for class terms.

• $\{x|\varphi \}\!\in \!\{y|\psi \}\leftrightharpoons \exists y(\forall x(x\!\in \!y\leftrightarrow \varphi )\wedge \psi )$;

• $\{x|\varphi \}=\{y|\psi \}\leftrightharpoons \forall x(\varphi \leftrightarrow \psi [x/y])$.

Depending on how we look at x as a variable or a=j a shorthand for $\{y|y\!\in \!x\}$ the class formulas $x\!\in \!y$ and $x\!\in \!C$ have different meanings. However, they are equivalent if we take the Extensionality Axiom ($FSA_1$).

Proposition 8

• (i) $FSA_1\models (x\!\in \!y)\leftrightarrow (\{z|z\!\in \!x\}\!\in \!{w|w\!\in \!y})$

• (ii) $FSA_1\models (x\!\in \!C)\leftrightarrow (\{z|z\!\in \!x\}\!\in \!\{w|w\!\in \!C\})$

Proof

We prove only the statement (i). Working in axiom system $\{FSA_1\}$ we have the following chain of semantic equivalences:

$$\begin{aligned} \{z|z\!\in \!x\}\!\in \!\{w|w\!\in \!y\}\equiv \exists u(\forall z(z\!\in \!x\leftrightarrow z\!\in \!u)\wedge u\!\in \!y)\equiv u(x=u\wedge u\!\in \!y)\equiv x\!\in \!y. \end{aligned}$$

$\square$

By using the above proposition we can define the following abbreviations:

• $C=D\leftrightharpoons \forall x(x\!\in \!C\leftrightarrow x\!\in \!D)$

• $C=y\leftrightarrow \forall x(x\!\in \!C\leftrightarrow x\!\in \!y)$

• $C\!\in \!x\leftrightharpoons \exists y(C=y\wedge y\!\in \!x)$

• $C\!\in \!D\leftrightharpoons \exists y(C=y\wedge y\!\in \!D)$

For the classical first order languages we have defined the simultaneous substitution of terms. This notion can be extended even to the class language. However, we have to make a careful distinction between substitution for variables and for class–terms. The only question is how substitute into a formula $x\!\in \!C$?

First let $\tau$ be a term belonging $Term_\sigma$. If so then take $(x\!\in \!C)[\tau /C]\leftrightharpoons x\!\in \!\tau$. Clearly $x\!\in \!\tau$ belongs to $cForm_\sigma$. In the case of class terms take $(x\!\in \!C)[\tau /C]\leftrightharpoons \varphi [x/y]$ where $\tau =\{y|\varphi \}$. This definition is comform with the fact that $x\!\in \!\{y|\varphi \}$ is just a shorthand for $\varphi [x/y]$. In the end if D is a class variable then take $(x\!\in \!C)[D/C]\leftrightharpoons x\!\in \!D$.

Without spelling out the whole definition we use the notation $\varphi [\tau _i/x_i]_i^{\ k}$ for the simultaneous substitution of terms $\tau _i$ for variables $x_i$, respectively.

Lemma 1

Let $\mathbf {V}\!\in \!cMod_\sigma$ and let $\varphi \!\in \!cForm_\sigma$ be arbitrary. Let us suppose that $var(\varphi )\cap cV=\{C_1,\ldots ,C_k\}$. Then for any class terms $\tau _1,\ldots ,\tau _n$ if $\mathbf {V}\models \varphi$ then $\mathbf {V}\models \varphi [\tau _i/C_i]_i^{\ k}$.

In order to handle classes axiomatically the axiom system $FSA_\sigma$ is to be appropriately extended. The extended axiom system denoted by $cFSA_\sigma$ consists of

• axioms which remain the same as they were in $FSA_\sigma$ dealing with sets only;

• axioms the scope of which is extended to classes;

• the extentions of the axiom schemas by allowing class formulas.

Namely, by extending the axiom system we get the following axiom system $cFSA_\sigma$ where variables $f , g , x , y , z , w, w_1 ,\ldots , w_n$ are from V and C, D are from cV.

• $FSA_0$ Existential axiom of atoms:

  

• $FSA_1$ Extensionality axiom:

  

• $FSA_2$ Empty set axiom:

  

• $FSA_3$ Significance axiom of atoms:

  

This axiom together with $FSA_1$ declares that though atoms have no elements they differ from the empty set 0.

• $FSA_4$ Foundation axiom:

  

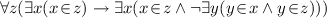
• $FSA_{5\sigma }$ Comprehension schema:

  

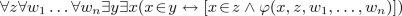
  $(\text {where }\varphi \!\in \!cForm_\sigma !)$

• $FSA_6$ Pairing axiom:

  

We remark that since classes have only sets as elements the Pairing Axiom is not extended to classes.

Before reformulating $FSA_7$ we remark that for any term t one can define its union by taking $\cup t=\{x|\exists y(x\!\in \!y\wedge y\!\in \!t)\}$. However, our original axiom states that if t is not proper then $\cup t$ is also not proper! Therefore, we have to use $FSA_7$ without any changes.

• $FSA_7$ Union axiom:

  

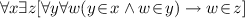
• $FSA_{8\sigma }$ Replacement scheme. For each $\sigma$-type formula $\varphi$:

  

  $(\text {where }\varphi \!\in \!cForm_\sigma )$

Similarly to the modification of the Comprehension schema we allow the use of class formulas in the scope of the Replecement schema as well.

• $FSA_9$ Finiteness axiom:

  

Now having the axiom system $cFSA_\sigma$ we clarify some notions. Let $\mathbf {V}=(\mathbf {A},\underline{Class})$ be an arbitrary class extention of $\mathbf {A}$.

• The elements of A are called objects.

• Let $a\!\in \!A$ be an object. If $\mathbf {V}\models \underline{atom}(x)[(a,x)]$ then a is said to be an $\underline{atom}$, otherwise it is a $\underline{set}$.

• The elements of $\underline{Class}$ are said to be classes.

• An object a and a class U are called equal iff $\mathbf {V}\models \forall y{(y\!\in \!x\leftrightarrow y\!\in \!C)} [(x,a)+(C,U)]$.

• A class $U\!\in \!\underline{Class}$ is called a proper class iff it is not equal to any object of $\mathbf {V}$. Namely U is a proper class if it satisfies the formula $\mathbf {V}\models \lnot \exists x(x=C)[(C,U)]$.

We redefine predicate ‘set’ by taking:

$$\begin{aligned} \underline{cset}(C)\leftrightharpoons \exists x(x=C\wedge \lnot \underline{atom}(x)). \end{aligned}$$

The $\lnot \underline{atom}(x)$ part of the conjunction is needed only when one substitutes a variable x for class-variable C:

$$\begin{aligned} \underline{cset}(C)[x/C]\equiv \exists y(y=x\wedge \lnot \underline{atom}(y)\equiv \lnot \underline{atom}(x)). \end{aligned}$$

Next we omit ‘c’ from the name of this redefined predicate because on sets the new and old meanings are the same.

The predicate ‘proper’ can be defined by taking:

$$\begin{aligned} \underline{proper}(C)\leftrightharpoons \lnot \exists x(x=C). \end{aligned}$$

According to the above defined predicates a class term $\tau$ is called relational or functional iff $Rel(\tau )$ or $Func(\tau )$ holds respectively.

The followings are two useful proper classes:

• $\underline{Universe}=\{x|x=x\}$;

• $\omega =\{x|Nat(x)\}$.