Abstract
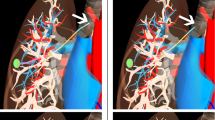
Concentric tube robots, or CTRs, are tentacle-like robots composed of precurved telescoping tubes (Fig. 1a) and are controlled by rotating and translating each individual tube [6]. Their dexterity and small diameter enable minimally-invasive surgery in constrained areas, such as accessing the pituitary gland via the sinuses. Unfortunately, their unintuitive kinematics make manually guiding the tip while also avoiding obstacles with the entire tentacle-like shape extremely difficult [19]. This motivates a need for new user interfaces and planning algorithms.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Similar content being viewed by others
Notes
- 1.
Computing the continuous Fréchet distance, is notoriously difficult [16]. Thus, we use the discrete variant, easily computed using dynamic programming [5]. Here, the “leash” between points on the two paths is computed only for a discrete set of points and serves as an approximation of the (continous) Fréchet distance.
- 2.
By a slight abuse of notation we use FK to map both points as well as paths in \(\mathcal {C}\)-space to points and paths in task space, respectively.
- 3.
By a slight abuse of notation we treat R both as the discrete reference path as well as the one-dimensional graph defined by this sequence of waypoints.
References
Atias, A., Solovey, K., Salzman, O., Halperin, D.: Effective metrics for multi-robot motion-planning. CoRR, abs/1705.10300 (2017)
Berenson, D., Srinivasa, S., Ferguson, D., Kuffner, J.: Manipulation planning on constraint manifolds. In: ICRA, pp. 625–632 (2009)
Burdick, J.: On the inverse kinematics of redundant manipulators: characterization of the self-motion manifolds. In: ICRA, pp. 264–270 (1989)
Dellin, C., Srinivasa, S.: A unifying formalism for shortest path problems with expensive edge evaluations via lazy best-first search over paths with edge selectors. In: ICAPS, pp. 459–467 (2016)
Eiter, T., Mannila, H.: Computing discrete Fréchet distance. Technical report, Citeseer (1994)
Gilbert, H., Rucker, D., Webster III, R.J.: Concentric tube robots: the state of the art and future directions. In: ISRR, pp. 253–269 (2013)
Haghtalab, N., Mackenzie, S., Procaccia, A., Salzman, O., Srinivasa, S.: The provable virtue of laziness in motion planning. In: ICAPS, pp. 106–113 (2018)
Har-Peled, S., Raichel, B.: The Frećhet distance revisited and extended. TALG 10(1), 3 (2014)
Holladay, R., Salzman, O., Srinivasa, S.: Minimizing task space Frećhet error via efficient incremental graph search. CoRR, abs/1710.06738 (2017)
Johnson, H., McCormick, M., Ibanez, L.: The ITK Software Guide Book 1: Introduction and Development Guidelines, vol. 1. Kitware Inc., New York (2015)
Koenig, S., Likhachev, M., Furcy, D.: Lifelong planning A*. Artif. Intell. 155(1–2), 93–146 (2004)
Kwong, S., He, Q.H., Man, K.F., Tang, K.S., Chau, C.W.: Parallel genetic-based hybrid pattern matching algorithm for isolated word recognition. Int. J. Pattern Recogn. Artif. Intell. 12(05), 573–594 (1998)
Pan, J., Chitta, S., Manocha, D.: FCL: a general purpose library for collision and proximity queries. In: ICRA, pp. 3859–3866 (2012)
ROS Industrial. Descartes (2015). Accessed 20 Apr 2018
Rucker, D.: The mechanics of continuum robots: model-based sensing and control. Ph.D. thesis, Vanderbilt University (2011)
Solovey, K., Halperin, D.: Sampling-based bottleneck pathfinding with applications to Fréchet matching. In: European Symposium on Algorithms, ESA, pp. 76:1–76:16 (2016)
Srinivasa, S., Johnson, A., Lee, G., Koval, M., Choudhury, S., King, J., Dellin, C., Harding, M., Butterworth, D., Velagapudi, P., Thackston, A.: A system for multi-step mobile manipulation: architecture, algorithms, and experiments. In: ISER, pp. 254–265 (2016)
Sriraghavendra, E., Karthik, K., Bhattacharyya, C.: Fréchet distance based approach for searching online handwritten documents. In: Document Analysis and Recognition, vol. 1, pp. 461–465. IEEE (2007)
Torres, L., Kuntz, A., Gilbert, H., Swaney, P., Hendrick, R., Webster III, R.J., Alterovitz, R.: A motion planning approach to automatic obstacle avoidance during concentric tube robot teleoperation. In: ICRA, pp. 2361–2367 (2015)
Wampler, C.: Manipulator inverse kinematic solutions based on vector formulations and damped least-squares methods. IEEE Trans. Syst. Man Cybern. 16, 93–101 (1986)
Wylie, T., et al.: The discrete Fréchet distance with applications. Ph.D. thesis, Montana State University-Bozeman, College of Engineering (2013)
Yao, Z., Gupta, K.: Path planning with general end-effector constraints: using task space to guide configuration space search. In: IROS, pp. 1875–1880 (2005)
Acknowledgments
We thank Bob Webster and his group at Vanderbilt University for numerous discussions on CTRs and for creating the CTR used here. We thank Rachel Holladay for her invaluable insight in discussing her previous work. This work was (partially) funded by the National Institute of Health R01 (#R01EB019335), National Science Foundation CPS (#1544797), National Science Foundation NRI (#1637748), National Science Foundation RI Award 1149965, the Office of Naval Research, the RCTA, Amazon, and Honda.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
1 Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Copyright information
© 2020 Springer Nature Switzerland AG
About this paper
Cite this paper
Niyaz, S., Kuntz, A., Salzman, O., Alterovitz, R., Srinivasa, S. (2020). Following Surgical Trajectories with Concentric Tube Robots via Nearest-Neighbor Graphs. In: Xiao, J., Kröger, T., Khatib, O. (eds) Proceedings of the 2018 International Symposium on Experimental Robotics. ISER 2018. Springer Proceedings in Advanced Robotics, vol 11. Springer, Cham. https://doi.org/10.1007/978-3-030-33950-0_1
Download citation
DOI: https://doi.org/10.1007/978-3-030-33950-0_1
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-33949-4
Online ISBN: 978-3-030-33950-0
eBook Packages: Intelligent Technologies and RoboticsIntelligent Technologies and Robotics (R0)