A Novel Multi-focus Image Fusion Based on Lazy Random Walks

Abstract

Most existing fusion methods usually suffer from blurred edges and introduce artifacts (such as blocking or ringing). To solve these problems, a novel multi-focus image fusion algorithm using lazy random walks (LRW) is proposed in this paper. Firstly, the sum of the modified Laplacian (SML) of each source image and a maximum operation rule are used to obtain the highly believable focused regions. Then, a lazy random walks based image fusion algorithm is presented to precisely locate the boundary of focused regions from the above highly believable focused regions in each source image. Experimental results demonstrate that the proposed algorithm can generate high quality all-in-focus images, avoid annoying artifacts and well preserve the sharpness on the focused objects. Our method is superior to the state-of-the-art methods in both subjective and objective assessments.

1 Introduction

Image quality improvement is an important task in computer vision. Due to the finite depth of field of optical lenses, objects of different distances in the same scene cannot be fully focused. However, in practice, we may need an image with all objects clearly visible, which requires every part of the image is in focus. Multi-focus image fusion, which merges the focus regions from a series of images of the same scene to construct a single image, is a popular way to solve this problem.

The existing multi-focus image fusion methods can be roughly classified into two categories: spatial domain based methods and transform domain based methods. Since the multi-scale decomposition can effectively extract the salient features of the image, the transform domain based methods can achieve good fusion effect [1, 2]. However, transform domain based methods have some disadvantages [3]: the first one is the selection of the decomposition tool. The second drawback is some information in low-contrast areas can be easily lost. Furthermore, slight image mis-registration will result in undesirable artifacts. Different from transform domain based methods, spatial domain based methods directly handle the intensity values of source images, and it selects pixels with more obvious features as the corresponding pixels of the fusion image. This kind of method is simple and effective, and sharpness information of source images can be well preserved in the fused image. The core issue of spatial domain based methods is the evaluation of sharpness. In order to effectively distinguish between the focus areas and the defocus areas, researchers have proposed a number of focus measures, such as sum of the modified Laplacian (SML) [4], multi-scale morphological gradient (MSMG) [5], etc. These focus measurement techniques usually perform well for focus region detection. However, the robustness of focus areas detection is insufficient for smooth areas, image noise and mis-registration, etc. Therefore, the spatial domain based methods often suffer from blocking artifacts and erroneous results at the smooth areas and the boundary of focused areas.

To detect focused areas well, some novel image fusion methods have been presented recently. These image fusion methods can be divided into two categories: the first one is using the “hole-filling” or morphology filter to filter the initial decision map. Firstly, this type of method uses some novel focus measures (LBP [3], surface area [6], convolutional neural network (CNN) [7], etc.) to obtain the initial decision map. Then the “hole-filling” or morphology filter is used to eliminate the noise in the initial decision map. Finally, the final decision map is obtained by the guided filtering to optimize the filtered decision map. These multi-focus image fusion methods can effectively alleviate the impact of noise in decision maps. Most of the focused regions of the source image are merged into the composite image, and the visual effect of the fused image is significantly improved. However, the robustness of the post-processing methods is insufficient, which will result in incomplete filling of larger “hole” or false filling of smaller focused regions and inaccurate locating of the position of boundary. The second one is using some optimization techniques (such as image matting method [8], random walk (RW) algorithm [9], etc.) to obtain the final fusion weight maps. These approaches can be impressively useful. The RW algorithm uses the first arrival probability to decide the label of each pixel. RW-based image fusion algorithms have the advantages of simple model and fast computation speed. However, the first arrival probability ignores the global relationship between the current pixel and other seeds. Therefore, the RW algorithm has the disadvantages that it cannot guarantee convergence to a stable state and the image processing results are not robust. In order to make full use of the whole relationship between the pixel and all seeds, Shen et al. proposes the LRW algorithm through adds the self-loop over the graph vertex to make the RW process lazy [10]. LRW-based superpixel algorithm obtains good boundary adherence in the weak boundary and complicated texture regions. Compared with the traditional RW algorithm, the LRW algorithm has two advantages. Firstly, the LRW algorithm effectively overcomes the problem of RW algorithm which cannot guarantee convergence to a stable state, so it improves the applicability of the algorithm. Secondly, the LRW algorithm uses the commute time of visual transition to depict the difference between pixels, which is more reasonable and appropriate in the simulation of biological vision, thus the LRW algorithm is more robust. On account of these advantages, the LRW algorithm is adopted in the proposed fusion method.

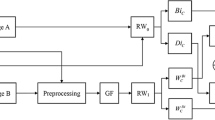
To address the weaknesses of existing multi-focus image fusion methods (such as spatial inconsistency, blurred edges, and vulnerability to mis-registration, etc.), we propose a novel method for multi-focus image fusion in this paper. The schematic diagram of our multi-focus image fusion method is shown in Fig. 1. The proposed method consists of four steps. Firstly, the SML is used to evaluate the focus score of each pixel locally for each source image. Secondly, the focus scores are forwarded to LRW to obtain the global probability maps. Then, we can find the accurate focused map of each source images by the probability maps. At last, the focused maps are used to fuse source images to obtain the all-in-focus image. Unlike many existing methods, the proposed method does not need post-processing to suppress the noise of decision map. This paper provides two contributions: (1) No parameters need to be adjusted during the highly believable focused regions detection. (2) We introduce the LRW algorithm into multi-focus image fusion. The remainder of this paper is organized as follows. In Sect. 2, we briefly review the LRW theory. Section 3 describes the proposed image fusion method in detail. The experimental results and discussions are presented in Sect. 4. Section 5 summarizes this paper.

Fig. 1.

Schematic diagram of the proposed multi-focus image fusion method

2 Lazy Random Walk Algorithm

The RW algorithm is a very popular approach for image segmentation [11], image fusion [9]. The RW algorithm uses the first arrival probability to decide the label of each pixel. However, the first arrival probability ignores the global relationship between the current pixel and other seeds. In 2014, Shen et al. proposes the LRW based superpixel algorithm and achieves good results [10]. Compared with the traditional RW algorithm, the LRW algorithm can guarantee convergence to a stable state, thus the LRW algorithm is more robust. Therefore, the LRW algorithm is used for multi-focus image fusion in this paper. In the LRW algorithm, we define an undirected graph $\varvec{G} = (\varvec{V},\varvec{E}\text{)}$ on a given image, where $\varvec{V}$ is the set of nodes and $\varvec{E} \subseteq \varvec{V} \times \varvec{V}$ is the set of edges. The LRW graph has the property that there is a non-zero likelihood that a lazy random walk remains at the original node through adds a self-loop over each vertex $v_{i}$. Then the adjacency matrix is defined as:

$$ \varvec{W}_{i,j} = \left\{ {\begin{array}{*{20}l} {1 - \alpha } \hfill & {{\text{if}}\,i = j} \hfill \\ {\alpha \cdot w_{i,j} } \hfill & {{\text{if}}\,v_{i} \,{\text{and}}\,v_{j} \,{\text{are}}\,{\text{the}}\,{\text{adjacent}}\,{\text{nodes}}} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(1)

where $\alpha \in (0,1)$ is lazy factor, $w_{i,j}$ is a function defined on $\varvec{E}$ that models the similarity between nodes $v_{i}$ and $v_{j}$. Since the Gaussian function has the property of geodesic distance, thus the edge-weight $w_{i,j}$ is defined as:

$$ w_{i,j} \, = \,{ \exp }( - \frac{{\left\| {g_{i} - g_{j} } \right\|^{2} }}{{2\sigma^{2} }}) $$

(2)

where $g_{i}$ and $g_{j}$ denote the image intensity values at two nodes $v_{i}$ and $v_{j}$, and $\sigma$ is the user defined parameter to control the sensitivity of the compatibility function to the difference of pixel values.

According to the adjacency matrix $\varvec{W}$ on the graph, the graph Laplacian matrix is defined as:

$$ \varvec{L}_{ij} = \left\{ {\begin{array}{*{20}l} {d_{i} } \hfill & {{\text{if}}\,i = j} \hfill \\ { - \alpha \cdot w_{i,j} } \hfill & {{\text{if}}\,v_{i} \,{\text{and}}\,v_{j} \,{\text{are}}\,{\text{the}}\,{\text{adjacent}}\,{\text{nodes}}} \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right. $$

(3)

where $d_{i} = \sum\limits_{{v_{j} \in N_{i} }} {w_{i,j} }$ is the degree of node $v_{i}$ defined on its neighborhood $N_{i}$. We can also write Eq. (3) as $\varvec{L} = \varvec{D} - \alpha \varvec{W}$, $\varvec{D} = diag(d_{1} ,d_{2} , \cdots d_{S} )$, $S$ is the size of image $I$.

Duo to the normalized Laplacian matrix is to be more consistent with the eigenvalues of adjacency matrices in spectral geometry and in stochastic process [12], so we use the normalized Laplacian matrix in this paper. The normalized Laplacian matrix is $\varvec{NL} = \varvec{I} - \alpha \varvec{D}^{ - 1/2} \varvec{WD}^{ - 1/2}$. The normalized commute time $\varvec{NCT}_{ij}$ of LRW denote the expected time for a lazy random walk that starts at one node $v_{i}$ to reach node $v_{j}$ and return to the node $v_{i}$, which is inversely proportion to the probability, so the closed-form of likelihoods probabilities of label $l$ is:

$$ \varvec{f}^{l} = 1 - \varvec{NCT}_{ij} = (\varvec{I} - \alpha \varvec{D}^{ - 1/2} \varvec{WD}^{ - 1/2} )^{ - 1} \varvec{y}^{l} $$

(4)

where $\varvec{I}$ is the identity matrix, $\varvec{y}^{l}$ is a $S \times 1$ vector where all the elements are zero except the seed pixels as 1.

3 Multi-focus Image Fusion Based on LRW

The problem of multi-focus image fusion is the problem of assigning larger weights to focused pixels and smaller weights to defocus pixels. To compute the fusion weight using LRW, we model the fusion problem into a graph. In the LRW algorithm, the commute time is a proper probability measurement of the similarity between the current pixel and the seed pixel. The shorter the commute time, the higher the similarity is, so the fusion weight is inversely proportion to the commute time. In the following subsections, the LRW based image fusion method will be explained in detail.

3.1 Focus Measure

The first step of the proposed method is to get the focus information of source image. In the literature [4], Huang performed a comparison of several focus measures in multi-focus image fusion and showed that SML generally outperform variance, energy of image gradient (EOG), and spatial frequency (SF). In the experiment, we found that accurate decision maps can be obtained by choosing different focus measures, and the difference between the decision maps is small. In this paper, the SML is chosen as the focus measure. More specifically, the SML [4] is defined as:

$$ \begin{aligned} {\mathbf{ML}}(x,y) = & \,\left| {2{\mathbf{gf}}(x,y) - {\mathbf{gf}}(x - 1,y) - {\mathbf{gf}}(x + 1,y)} \right| \\ { + } & \,\left| {2{\mathbf{gf}}(x,y) - {\mathbf{gf}}(x,y - 1) - {\mathbf{gf}}(x,y + 1)} \right| \\ \end{aligned} $$

(5)

$$ {\mathbf{SML}}(x,y) = \sum\limits_{m = - r}^{r} {\sum\limits_{n = - r}^{r} {{\mathbf{ML}}^{2} (x + m,y + n)} } $$

(6)

where $r$ is the radius of local patch and ${\mathbf{gf}}(x,y)$ is the intensity value of gray image.

3.2 Highly Believable Focused Region Detection

This part comprises of three steps to detect the highly believable focused regions.

• Step 1: We use Eq. (6) to calculate the focus measure map $\varvec{FM}_{n} ,n = 1,2, \cdots N$ for each source image $\varvec{I}_{n}$, where $N$ is the number of source images.

• Step 2: According to the focus measure maps of the source images obtained in step 1, a maximum focus measure map $\varvec{mFM}$ is calculated:

  $$ \varvec{mFM}(x,y) = \mathop {\hbox{max} }\limits_{n} \{ \varvec{FM}_{n} (x,y)\} $$

  (7)

• Step 3: The highly believable focused region of the $n$th source image $\varvec{HFR}_{n}$ is calculated:

  $$ \varvec{HFR}_{n} (x,y)\, = \,\left\{ {\begin{array}{*{20}l} {1\quad {\text{if}}\;\varvec{FM}_{n} (x,y) > \mathop { \hbox{max} }\limits_{m,m \ne n} \{ \varvec{FM}_{m} (x,y)\} } \hfill \\ {\quad \quad \quad \quad \& \varvec{FM}_{n} (x,y) > T} \hfill \\ {0\quad {\text{otherwise}}} \hfill \\ \end{array} } \right. $$

  (8)

  The threshold $T$ is set to the average value of image $\varvec{mFM}$. $\varvec{HFR}_{n} (x,y) = 1$ indicates that the pixel at $(x,y)$ is considered as a highly believable focus position in the $n$th source image.

3.3 Image Fusion Based on LRW

The focused regions of the source images are sparse obtained according to Eq. (8). In the final fusion part, the weight map obtained by the $\varvec{HFR}_{n}$ is meaningless (the values of all weight maps’ partial corresponding positions are zero). Therefore, we need to generate a dense weight map based on the sparse $\varvec{HFR}_{n}$. The LRW algorithm described in Sect. 2 is particularly applicable to solve this problem. We can regard the highly believable focused region as the seed points of LRW algorithm then use the LRW algorithm to obtain the likelihoods probabilities between the pixels and seed points in each position of the source images. Thereby we can obtain the accurate focus areas of each source image. For the source image $\varvec{I}_{n}$, we obtain the positions of seed points of focus areas $\varvec{fp}_{n}$ and defocus areas $\varvec{dfp}_{n}$ according to the highly believable focused regions obtained in Sect. 3.2, respectively:

$$ \varvec{fp}_{n} = \{ (x,y)|\varvec{HFR}_{n} (x,y) = 1\} $$

(9)

$$ \varvec{dfp}_{n} = \{ (x,y)|\varvec{HFR}_{m,m \ne n} (x,y) = 1\} $$

(10)

After obtaining the position sets $\varvec{fp}_{n}$ and $\varvec{dfp}_{n}$, we use Eq. (4) to calculate the likelihood probability map $\varvec{p}_{n}^{fp} (x,y)$ of focus areas and the likelihood probability map $\varvec{p}_{n}^{dfp} (x,y)$ of defocus areas for each position of source image $\varvec{I}_{n}$. So we can get the final decision map of the $n$th source image by:

$$ \varvec{W}_{n} (x,y) = \left\{ \begin{aligned} 1\quad {\text{if}}\;\varvec{p}_{n}^{fp} (x,y) > \varvec{p}_{n}^{dfp} (x,y) \hfill \\ 0\quad {\text{if}}\;\varvec{p}_{n}^{dfp} (x,y) \ge \varvec{p}_{n}^{fp} (x,y) \hfill \\ \end{aligned} \right. $$

(11)

Finally, we obtain the fused image $\varvec{F}$ as follows:

$$ \varvec{F} = \sum\limits_{n = 1}^{N} {\varvec{W}_{n} \varvec{I}_{n} } $$

(12)

4 Experimental Results and Analysis

4.1 Experimental Settings

Experiments are performed on 26 pairs of multi-focus source images. 20 sets of them come from a new multi-focus dataset called “Lytro” [13], and another 6 sets which are widely used in multi-focus fusion research. A portion of source image pairs are shown in Fig. 2. We compare the proposed method with three representative fusion methods which are image matting based image fusion (IM) [8], boundary finding based image fusion algorithm (BF) [5] and convolution neural network based method (CNN) [7]. In our experiments, the parameters of LRW are set to $\sigma = 0.01$ and $\alpha = 0.9992$, respectively. To quantitatively assess the performances of different methods, five widely recognized objective fusion metrics are applied in our experiments. They are the normalized mutual information (Q_NMI) [14], image feature based metrics (Q_G) [15], image structural similarity based metric (Q_Y) [16], human perception-based metric (Q_CB) [17] and the visual information fidelity fusion (Q_VIFF) [18]. For all the five evaluation metrics, a larger value indicates a better fusion performance.

Fig. 2.

A portion of source image sets used in our experiments

4.2 Qualitative and Quantitative Comparison

The decision maps and their corresponding fused images obtained by different methods are shown in Figs. 3, 4 and 5, respectively. For clearer comparison, the local magnified regions of fused images are presented in the third row of each figure. It can be seen from the fusion results that the IM method made noticeable artifacts in the transitional regions (the boundaries between focused and defocused regions) and partial defocus regions are also selected in the fused image (Stadium’s steel mesh), which owing to the image matting algorithm is difficult to completely accurate extract the focus areas of the source image. The BF method selected many blurred regions of source image into the fused image (golf club). In Fig. 5(b), the BF method failed to fuse the stadium images that captured at complex scenes, and the steel mesh in the fused image is completely taken from the defocus regions. The CNN and the proposed method obtained clearer fused images with high contrast. The visual effects of fusion results are very good. The CNN method performs some post-processing on decision maps (such as “hole-filling” and guided filtering), which will cause the fused image obtained by the CNN method to appear slightly blurred at the focus boundary and misjudge the isolated small focused region in the source images (red box in the “Golf” fused image). Figures 3, 4 and 5(d) shows the result of our method. We can see that our method is able to accurately identify the focused regions and produces the clearest fused images.

Fig. 3.

The “Golf” fused images and decision maps by different fusion methods. First row: fused images. Second row: decision maps. Third row: local magnified regions. (Color figure online)

Fig. 4.

The “Temple” fused images and decision maps by different fusion methods. First row: fused images. Second row: decision maps. Third row: local magnified regions.

Fig. 5.

The “Stadium” fused images and decision maps by different fusion methods. First row: fused images. Second row: decision maps. Third row: local magnified regions. (Color figure online)

The average objective assessment values of 26 pairs testing images are listed in Table 1. Each bold value in Table 1 indicates the highest value in the corresponding row. As can be seen from Table 1, the proposed method has obtained the highest objective evaluation value in all five metrics which indicates that the proposed method has better performance in comparison to other methods and reflects the stability of the proposed fusion method.

Table 1. The average objective assessments of different image fusion methods

4.3 Computational Complexity

In the initialization step, the source images are converted to gray scale for calculating SML. The complexity of this step is $O(NK)$, where $K$ is the number of pixels in source image and $N$ is the number of source images. The complexity for computing the SML feature is approximately $O(NK)$. We use the symmetric and highly sparse Laplacian graph to compute the LRW algorithm by solving the large sparse linear system. The complexity of the LRW algorithm is about $O(NK^{2} )$. With only linear operations involved, the complexity of the fusion step is $O(NK)$. Therefore, the total complexity of our algorithm is $O(NK^{2} )$. The average computational time for processing all the 26 pairs testing images by different fusion methods is listed in Table 2. All the fusion methods Matlab implementations were executed on the same computer with a 2.20-GHz CPU and 12-GB memory available for Matlab. As can be seen from Table 2, the BF and the proposed method are the two most efficient methods compared with other methods. The IM method uses the image matting technique to obtain the final fusion weight maps, so the running time of IM method is slightly slower than the one of our method. Although CNN can quickly produce fused image using GPU, the running time with CPU is too long and up to about 225 s.

Table 2. The average running time of different fusion methods

5 Conclusion

In this paper, an effective and robust multi-focus image fusion algorithm based on LRW is proposed. The proposed method first obtains a highly believable focus region in each source image by comparing the focus score of each pixel then forwards the highly believable focus information to LRW algorithm to obtain the global optimization probability maps. Since LRW is able to make full use of the strong correlations between pixels, the proposed method can accurately extract the focus regions of each source image. Experimental results show that the proposed method achieves better performance than the compared fusion methods, both in visual effects and objective evaluations.