Abstract
This paper describes an approach to segment liver shape from abdominal CT sequences, required by the analysis of liver diseases. A rough segmentation is first conducted via a customized Fast Marching method to obtain an approximate 3D liver region for subsequent procedure. Then, an improvement of GMM-EM algorithm is made to extract the accurate liver region. Experimental results, evaluated on non-tumor series and tumor series of 10 cases, show that the proposed method performs better than several other typical segmentation models in running time and precision.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Among the most common malignant diseases, liver diseases have the highest incidence rate in the world. Usually, liver diseases can be diagnosed in computed tomography (CT) images and the liver boundary delineation is a key step in the liver sequence analysis. While manual delineation being time-consuming and inefficient, automatic delineation is still facing with difficulties in that the liver is packed with organs of similar-looking tissues with fuzzy boundaries in grayscale.
In order to be more efficient and accurate in segmentation, various methods have been developed to improve the performance of the image processing approaches in liver extraction, including adaptive intensity thresholding [1], region growing, convolutional neural network [2] and so on.
Normally, there are three main stages in liver shape extraction, i.e., noise suppression, ROI initialization and final extraction. Many approaches concentrate on the initialization for the ROI [3], yet they fall short of accuracy because of the variability of liver shapes. Moreover, being highly dependent on initialization, some critical problems such as over-segmentation remain unsolved. In order not to count on initialization and iteration, a single-block linear detection model is presented [4]. But it is suffered from blurred edges between liver and abdominal wall. A customized level set method [5] is then proposed to segment liver shapes with an automatic seed point identification method and achieves good performance. However, the seed points selection is performed under the threshold of empirical value, which means the method is not robust enough.
In order to enhance the performance of liver segmentation, we introduce a hybrid segmentation model. For a given abdominal CT sequence, a few seed points are manually selected after image pre-processing. Then a rough segmentation is conducted with a customized Fast Marching Method (FMM). We further make an improvement of GMM-EM [6] for a finer segmentation.
The remainder of this paper is organized as follows. The proposed hybrid method is introduced in Sect. 2 followed by the corresponding experiment in Sect. 3. We conclude the paper in Sect. 4.
2 Method
Let \( I\, = \,\{ I_{n} :D\, \to \,{\mathbb{R}}, \, n\, = \,1,\, \ldots ,\,L\} \) be an liver CT sequence of L consecutive slices, where each slice In is an image defined on a rectangular grid D = {1, …, r} × {1, …, c} of r rows and c columns. Here we are concerned with the 3D characteristics of the CT sequence and prefer to denote D= D × {1, …, L} and Dn = D × {n}. Therefore the CT sequence has the volumetric representation as \( \varvec{I}:\varvec{D}\, \to \,{\mathbb{R}} \) . Our objective is then to extract the liver region \( \varvec{\varOmega} \) from D, which is called the region of interest (ROI), \( \varvec{\varOmega} \, \subset \,\varvec{D} \). Correspondingly, the ROI on slice n is \( \varOmega_{n} \, = \,D_{n} \, \cap \,\varvec{D} \).
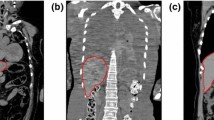
To invoke FMM [7,8,9], let \( \zeta \left( {t):[0,\infty } \right)\, \to \,{\mathbb{R}} \) be a marching closed contour in In and F be the speed of propagation. Then we have \( \partial \)ζ/\( \partial \)t = |∇ζ|F as the basic formulation of the level set equation. The essential idea of level set is to embed the marching contour as the zero set \( \tau \left( {s,t} \right) = 0 \) of \( \tau \left( {s,t} \right) = \pm d \), where \( s\, \in \,{\mathbb{R}} \) and d is the distance from s to ζ(t). The ζ(t) changes the topology of \( \tau \left( {s,t} \right) \) when the ζ(t) is propagating [10]. The ζ(t) is the red one and \( \tau \left( {s,t} \right) \) is the blue one in Fig. 1.
In FMM, the F is restricted into a one-way speed term at time t, i.e.
where |∇In | is the magnitude of the gradient [11] and α < 0 and β > 0 are constants that define the region of the image we are interested in. Our works on image preprocessing, consisting of the noise suppression, the edges enhancement and the calculation of F, follow the method in reference [12] implemented in the segmentation toolkit ITK [13].
Our segmentation model consists of two main ingredients, a customized FMM and an improved GMM-EM; the complete flowchart is shown in Fig. 2.
Afterwards, several slices In are chosen from I such that \( \varOmega_{n} \ne \emptyset \) in an interval of L/4 to L/3 slices. Then multiple points on these slices are manually selected as seed points, the number of which on each slice is according to the area of its ROI. For instance, we select 5 to 9 points for a large ROI and 1 to 3 points for a small ROI; see Fig. 3. The experiment in [14] shows that the multiple seed points strategy does greatly help upon liver segmentation when using FMM.
2.1 Customized FMM
In this part, a customized FMM is described to extract \( \varvec{\varOmega} \) from I. Moreover, a Gaussian image pyramid conducted by a series of down-sampling operation is employed in this pipeline. The Gaussian image pyramid approach is widely used in feature extraction, and it is proved to be facilitated in saving the pivotal feature in sampling operation [15]; the whole flow chart is presented in Fig. 4.
In practice, the size of D is usually 512 × 512. In order to shorten the processing time, here D is down sampled to 128 × 128 before preprocessing. Then we applied FMM twice to extract \( \varvec{\varOmega} \) from I.
In the 1st FMM, the seed points we set before will start to propagate and finally result in obtaining a coarse \( \varvec{\varOmega} \). Then a minimum bounding box algorithm [16] is to enclose the \( \varOmega_{n} \) in In by a square gird and form a minimum cuboid to contains the rough \( \varvec{\varOmega} \) as far as possible. It is not accurate enough because of the similar gray intensity of other organ edges. Especially in the similar gray intensity area such as adjacent edges between organs (Fig. 5), the propagation of the liver contour will not stop until the propagating time we set is arrived [17].
Then comes the 2nd FMM to get a finer \( \varOmega_{n} \). Here we take every 3 points on the liver surface as a set, 2 of them considered as alive points which will not be readjusted and the 1 left as trait point that needs to be readjusted [18]. Then the points on the surface are divided into two groups, the alive point group and the trait point group.
Now, we set another arrival time smaller than that in the 1st FMM and the trait points are readjusted when the time is arrival. In addition, in order to smoothen sharp burr edges, mathematical morphology methods, such as erosion and dilate, are used. The comparison between the rough ROI and its finer version is shown in Fig. 6. The region enclosed in blue represents the ROI. It can be seen that the FMM in the second round indeed provides better contours.
The FMM is still a low robustness algorithm in segmentation and has the problem of leaking into adjacent structures. In recent years, many researchers have done a lot in improving the FMM, such as adaptive arrival time [19], fuzzy generalized FMM [20, 21] and Fast Marching Spinning Tree [22]. These methods actually perform better than the traditional FMM, but the main problem, leaking to adjacent structures, is still unsolved. In the next part, we propose a new way to solve it by using improved GMM-EM which classifies the \( \varvec{I}|_{\varvec{\varOmega}} \) into two clusters, the false liver cluster and the true liver cluster.
2.2 Improved GMM-EM
For a slice In: D → R, the GMM of In means that, for a pixel p = (x, y) ∈ D, its probability density function f is assumed to be a weighted sum of K Gaussian distributions Gi–Ni(\( \mu_{i} \), \( \sigma_{i} \)) of mean μi and covariance σi with weight \( \pi_{i} \), i∈{1, …, K}, i.e.
where \( \pi_{i} \) sum up to 1. Let Ci ⊂ D be the cluster i such that \( \bigcup\nolimits_{i = 1}^{K} {C_{i} = D} \). Then the objective of GMM is to classify D into C1, …, CK.
The EM algorithm is one of the general solutions to acquire parameters (\( \mu \),\( \sigma \),\( \pi \)) for GMM and it can be divided into two step: E-step and M-step. More details are shown in Ref. [23].
In E-step, the main task is to calculate the posterior probability of the k-th Gaussian distribution Nk by randomly setting parameters \( \left( {\mu_{k} ,\sigma_{k} ,\pi_{k} } \right) \), k ∈ {1, …, K}. After that, to each pixel p, the generative probability from Nk can be described as
In the M-step, denoting rc as the number of p in D, we can re-estimate the parameters \( \left( {\mu_{k} ,\sigma_{k} } \right) \) with the results Pk and p:
and update the weight \( \pi_{k} \) of the k-th distribution as
Finally, alternating the E-step and M-step until the value of the likelihood function converges and these updated parameters (\( \mu \), \( \sigma \), \( \pi \)) are used in the GMM to classify D.
The random mean, covariance and weight will increase the computational cost. Our improvement is to apply K-means++ to approximate the parameters (\( \mu \), \( \sigma \), \( \pi \)) to restrain the impact of randomness [24]; a description of the algorithm is described in Table 1.
After applying the improved GMM-EM, the \( \varvec{I}|_{\varvec{\varOmega}} \) is divided into two categories which are the true liver area and the false liver area. Then we reserve the true liver area and draw its rim. Therefore, we not only gain an accurate \( \varvec{\varOmega} \) but also solve the leakage problem. The final result is shown in Fig. 7.
3 Experimental Results
In order to evaluate our proposed method, we sampled liver CT dataset from Sun Yat-Sen Univ. Affiliated Tumor Hospital anonymously. The dataset was comprised of tumor or non-tumor cases from 10 patients, including 6 non-tumor cases (01–06), 2 close tumors (07, 08), and 2 open tumors (09, 10), each of consisting of an average of 300 CT slices. Each abdominal CT series was in a resolution of 512 × 512 in scale with a thickness of 3 mm.
Besides, we had the contour results of liver drawn manually from clinicians so that we could apply the Dice Similarity Coefficient (DSC) to evaluate the accuracy of our method. For ground truth image A and the predicted image B, their DSC defined as DSC(A, B) = 2|A ∩ B|/(|A| + |B|). The DSC of value 0 meant there was no overlap between the segmented region and ground truth while the value 1 meant perfect segmentation. We also used classification criteria evaluation method, such as Intersection-over-Union (IoU) and Accuracy, to do more objective analysis, which defined as: IoU = TP/(FP + TP + FN), Accuracy = (TP + TN)/(TP + TN + FN + FP), where TP denoted the number of true positive pixels, TN denoted the number of true negative pixels, FP denoted the number of false positive pixels and FN denoted the number of false negative pixels.
Firstly, we compared the GMM-EM and the improved GMM-EM under the same \( \varvec{I}|_{\varvec{\varOmega}} \) in run time. Apparently, our improvement was effective on reducing computing time according to the statistics (Fig. 8). The improvement achieved 83 s in average while unimproved method cost 169.6 s in average.
Also, we developed a comparative experiment upon the classification results from GMM-EM and improved GMM-EM, and the reference results were drawn by clinicians. We could infer that the improved GMM-EM performed better than the GMM-EM in accuracy from Table 2.
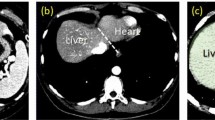
Especially in dealing with redundant areas in the \( \varvec{I}|_{\varvec{\varOmega}} \), the improved GMM-EM reserved more features than the GMM-EM, which could gain liver contour accurately. The red circle denoted to the redundant area and the blue one was the failure. Both of the results had done the fill-hole operation.
We noticed that Ina [25] developed a method comprised of level set and K-mean on the liver shape segmentation. The essential idea of this method is to classify liver CT into 4 clusters and to draw the liver contour from those clusters. Also, Pankaj et al. [26] proposed a similar hybrid method to do hemorrhage segmentation, which consists of fuzzy c-mean (FCM) and a modified version of distance regularize level set evolution (MDRLSE). It applies FCM to do classification on brain CT and selects relative cluster as an initialization for MDRLSE to process hemorrhage area, which reduces the number of iterations in level set.
In order to figure out the performance of our method, we conduct a comparative experiment with the above mentioned methods. All of them are conducted on the same dataset and circumstances. See Table 3 for the evaluation. The performance of ours in segmenting the non-tumor liver sequence is better than the others. However, due to the large difference of the gradient between the tumor and the liver parenchyma, the accuracy drops suddenly when processing liver tumor series (Fig. 9).
The representative results are presented in Fig. 10. In the third horizontal group, being affected by the tumor area, the contour shrinks into the liver area, which lowers the accuracy of segmentation.
On the edge of the liver, the Ina’s method is susceptible to the region of the similar gradient mutation and therefore fails to accurately segment the entire liver contour. Although the Pankaj’s method performs better than the Ina’s method, it still cannot segment liver completely. Our method allows the contour front to propagate into abdominal wall and tumor area while detecting the entire liver shape, and then the improved GMM-EM algorithm is applied to intercept and remove the redundant contour, so as to solve the problem of leaking to adjacent structures.
In Fig. 11, we rebuild results above in 3D for objective comparison. Compared to the other methods, the result of ours is more reductive to the ground truth. The coarse boundary which leaks to other structures slightly in 2D, can cause a large error in 3D by the other methods.
4 Conclusion
This paper proposes a model combining level set method and classification algorithm. Firstly, the first time FMM is used for rough segmentation. The minimum bounding box algorithm is used to search the three-dimensional liver region so as to remove uninterested region and shorten the processing time. And then the second time FMM is further applied on the result of the first time FMM. Thirdly, we extract the finer liver region by using the binary form to search a corresponding region in the original CT sequence. Finally, the GMM-EM algorithm initialized by K-Means++ divides the corresponding region into two classes, the true liver region and the false liver region. The leaking edge problem is solved by our method. The experimental results show that, our method averagely achieves 0.923 in IoU and 0.978 in DSC evaluation on segmenting the tumor-free liver sequence, which performances better than the other methods. But the performance is poor when segmenting the tumor liver sequence. Next, in the future work, we will develop tumor segmentation algorithm to make up this shortcoming.
References
Farzaneh, N., Habbo-Gavin, S., Soroushmehr, S.M.R., Patel, H., Fessell, D.P., Ward, K.R., et al.: Atlas based 3D liver segmentation using adaptive thresholding and superpixel approaches. In: 2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 1093–1097. IEEE, New Orleans (2017)
Lu, F., Wu, F., Hu, P., Peng, Z., Kong, D.: Automatic 3d liver location and segmentation via convolutional neural network and graph cut. Int. J. Comput. Assist. Radiol. Surg. 12(2), 171–182 (2017)
Chen, Y., Wang, Z., Hu, J., Zhao, W.: The domain knowledge based graph-cut model for liver CT segmentation. Biomed. Signal Process. Control 7, 591–598 (2012)
Huang, L., Weng, M., Shuai, H., Huang, Y., Sun, J., Gao, F.: Automatic liver segmentation from CT images using single-block linear detection. Biomed. Res. Int. 2016, 1–11 (2016). Hindawi
Yang, X., et al.: Segmentation of liver and vessels from CT images and classification of liver segments for preoperative liver surgical planning in living donor liver transplantation. Comput. Meth. Programs Biomed. 158, 41–52 (2018)
Xia, Y., Ji, Z., Zhang, Y.: Brain MRI image segmentation based on learning local variational Gaussian mixture models. Neurocomputing 204, 189–197 (2016)
Osher, S., Sethian, J.A.: Fronts propagating with curvature-dependent speed: algorithms based on Hamilton Jacobi formulations. J. Comput. Phys. 79, 12–49 (1988)
Sethian, J.A.: A fast marching level set method for monotonically advancing fronts. Proc. Natl. Acad. Sci. 93(4), 1591–1595 (1996)
Ho, H., Bier, P., Sands, G., Hunter, P.: Cerebral artery segmentation with level set methods. In: Proceedings of Image and Vision Computing New Zealand, pp. 300–304. Hamilton, New Zealand, December 2007
Yan, J., Zhuang, T.: Applying improved fast marching method to endocardial boundary detection in echocardiographic images. Pattern Recogn. Lett. 24(15), 2777–2784 (2003)
Campadelli, P., Casiraghi, E., Pratissoli, S.: Fully automatic segmentation of abdominal organs from CT images using fast marching methods. In: 21st IEEE International Symposium on Computer-Based Medical Systems, pp. 1–5. IEEE, Jyvaskyla, Finland (2008)
Lee, J., et al.: Efficient liver segmentation using a level-set method with optimal detection of the initial liver boundary from level-set speed images. Comput. Methods Programs Biomed. 88, 26–38 (2007)
Ibáñez, L., et al.: The ITK Software Guide. 2nd ed., Kitware, Inc., Clifton Park (2005)
Yang, X., Yu, H.C., Choi, Y., Lee, W., Wang, B., Yang, J., et al.: A hybrid semi-automatic method for liver segmentation based on levelset methods using multiple seed points. Comput. Methods Programs Biomed. 113, 69–79 (2014)
Ali, H., Elmogy, M., El-Daydamony, E., Atwan, A.: Multi-resolution MRI brain image segmentation based on morphological pyramid and fuzzy c-mean clustering. Arabian J. Sci. Eng. 40(11), 3173–3185 (2015)
Campadelli, P., Casiraghi, E., Esposito, A.: Liver segmentation from computed tomography scans: a survey and a new algorithm. Artif. Intell. Med. 45(2–3), 185–196 (2009)
Gómez, J.V., Álvarez, D., Garrido, S., Moreno, L.: Fast Methods for Eikonal equations: an experimental survey. IEEE Access 7, 39005–39029 (2019)
Capozzoli, A., Curcio, C., Liseno, A., Savarese, S.: A comparison of Fast Marching, Fast Sweeping and Fast Iterative Methods for the solution of the eikonal equation. In: 21st Telecommunications Forum Telfor (TELFOR), pp. 685–688. IEEE, Belgrade (2013)
Breuß, M., Cristiani, E., Gwosdek, P., Vogel, O.: An adaptive domain-decomposition technique for parallelization of the fast marching method. Appl. Math. Comput. 218(1), 32–44 (2011)
Forcadel, N., Guyader, C.L., Gout, C.: Generalized fast marching method: applications to image segmentation. Numer. Algorithms 48, 189–211 (2008)
Baghdadi, M., Benamrane, N., Sais, L.: Fuzzy generalized fast marching method for 3d segmentation of brain structures. Int. J. Imaging Syst. Technol. 27(3), 281–306 (2017)
Ascoli, Giorgio A., Hawrylycz, M., Ali, H., Khazanchi, D., Shi, Y. (eds.): BIH 2016. LNCS (LNAI), vol. 9919, pp. 52–60. Springer, Cham (2016). https://doi.org/10.1007/978-3-319-47103-7
Portela, N.M., Cavalcanti, G.D.C., Ren, T.I.: Semi-supervised clustering for MR brain image segmentation. Expert Syst. Appl. 41(4), 1492–1497 (2014)
Kapoor, A., Singhal, A.: A comparative study of K-Means, K-Means++ and Fuzzy C-Means clustering algorithms. In: 3rd International Conference on Computational Intelligence & Communication Technology (CICT), pp. 1–6. IEEE, Palo Alto (2017)
Singh, I.: Segmentation of liver using hybrid K-means clustering and level set. Int. J. Adv. Res. Comput. Sci. Software Eng. 5(8), 742–746 (2015)
Singh, P., Khanna, V., Kamal, M.: Hemorrhage segmentation by fuzzy c-mean with Modified Level Set on CT imaging. In: 5th International Conference on Signal Processing and Integrated Networks (SPIN), pp. 550–555. IEEE, Noida (2018)
Acknowledgement
This work is supported by the Science and Technology Planning Project of Guangdong Province with grant numbers 2017B010110007 and 2017B010110015.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Huang, W., Zhan, Y., Yang, R. (2019). A Hybrid Model for Liver Shape Segmentation with Customized Fast Marching and Improved GMM-EM. In: Zhao, Y., Barnes, N., Chen, B., Westermann, R., Kong, X., Lin, C. (eds) Image and Graphics. ICIG 2019. Lecture Notes in Computer Science(), vol 11902. Springer, Cham. https://doi.org/10.1007/978-3-030-34110-7_41
Download citation
DOI: https://doi.org/10.1007/978-3-030-34110-7_41
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34109-1
Online ISBN: 978-3-030-34110-7
eBook Packages: Computer ScienceComputer Science (R0)