Abstract
In the field of cognitive electronic warfare (CEW), unmanned combat aerial vehicle (UCAV) realize moving targets tracking is a prerequisite for effective attack on the enemy. However, most of the traditional target tracking use intelligent algorithms combined with filtering algorithms leads to the UCAV flight motion discontinuous and have limited application in the field of CEW. This paper proposes a continuous control optimization for moving target tracking based on soft actor-critic (SAC) algorithm. Adopting the SAC algorithm, the deep reinforcement learning technology is introduced into moving target tracking train. The simulation analysis is carried out in our environment named Explorer, when the UCAV operation cycle of is 0.4 s, after about 2000 steps of iteration, the success rate of UCAV target tracking is above 92.92%, and the tracking effect is improved compared with the benchmark.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Deep reinforcement learning (DRL) has achieved great success in many domains, such as automatic driving, robot control, path planning and so on. Deep learning has strong perception ability, but lacks certain decision-making ability; while reinforcement learning has decision-making ability, and has no way to deal with perception problems. Therefore, combining the advantages of the two and complementing each other provides a solution to the perceptual decision-making problem of complex systems [1]. Applying this method to UCAV, DRL can make decision for UCAV flight without knowing or limited understanding of the environment, and plan the best flight route.
In recent years, many methods are used to solve the problem of target tracking. For example, intelligent algorithms [2] and Kalman filter [3]. However, most of the methods are computationally intensive and have limited applications in complex problems. Zhao hui presented a fusion tracking algorithm of fire solution for MMW/Tv combined guidance UCAV based on IMM-PF [4]. However, the tracking trajectory is discrete and the trajectories need to be synthesized. Wu proposed a square root orthogonal Kalman filter (SRQKF) algorithm to realize target tracking [5], but it increased the computational complexity and took a long time. Therefore, to relieve the abovementioned drawback, Sun proposes a time method for autonomous vehicle tracking moving target based on regularized extreme learning machine (relm). Typical Q-learning algorithm was used to generate strategies suitable for autonomous navigation [6], but its force constraints were not considered.
With the development of deep reinforcement learning methods, more methods are used to solve UCAV target tracking or navigation problems. However, most of the papers do not consider UCAV’s flight action and constraints in three-dimensional (3D) space or discretize UCAV flight action, so it is difficult to apply UCAV to the actual scene.
In this paper, we propose a continuous control optimization for moving target tracking based on soft actor-critic (SAC) algorithm. Takes full account of UCAV flight environment and 3D space action characteristics, and carefully designs reward conditions. The SAC algorithm in deep reinforcement learning is used to train UCAV and complete the moving target tracking. Finally, the effectiveness of the method is demonstrated by experimental simulation. The simulation experiments verify the effectiveness of the proposed method.
The rest of the paper is organized as follows. Section 2 describe the problem of moving target tracking. In Sect. 3, the DRL and SAC algorithm are introduced. Results and related discussion are provided in the following section. The conclusion will be discussed in the last section.
2 Moving Target Tracking Research
Aiming at the traditional target tracking model is two-dimensional (2D) and UCAV motion is discontinuous. In this paper, SAC algorithm of deep reinforcement learning algorithm is used to train UCAV to track moving targets in 3D continuous model. This work mainly refers the CEW in [7].
2.1 Map
In order to view the flight trajectory of UCAV and moving target conveniently, we define a flight map (15 km × 15 km) named Explorer, Because it is difficult to visualize continuous motion in three-dimensional (3D) space on the dimension of altitude, so projected it into a (2D) plane in the negative direction of the Z-axis, and the flight altitude information is expressed numerically in the attribute box on the right side (Fig. 1).
2.2 Tracking Structure
A modular moving target track system is proposed for the target action continuous. Different parts of tracking system are shown in Fig. 2, and will be elaborated in detail in the following sections.
2.3 Confrontation Model and Training Constraints
In order to simulate the actual battlefield environment more realistically, we take full account of UCAV’s flight state and action constraints in 3D space and design the reward conditions of UCAV.
States
At any time \( t \), the state of the UCAV can be expressed as:
where \( \textit{CON} \) represents a function used to concatenate vectors.
The \( [dx_{t} ,dy_{t} ,dh_{t} ] \) is relative displacement of UCAV and moving target, \( [dv_{x,t} ,dv_{y,t} ,dv_{z,t} ] \) is relative velocity of UCAV and moving target. The transformation formula between Z-axis coordinates of any point in space and ground height:
where \( R \) is the radius of the earth and \( h \) is the height from UCAV to the surface of the earth.
In our environment Explorer, we only consider the case of 1v1, that is, a UCAV tracks only one moving target. The trajectory of the UCAV tracking moving target is shown as Fig. 3.
Action
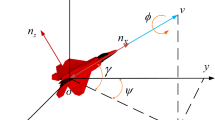
In the actual battlefield, UCAV cannot change the flight speed, direction, position and other information arbitrary and quickly because of its physical constraints. The constraints must be well considered in order to design UCAV flight action (Fig. 4).
According to [8], define the UCAV’s constraint reference frame and the local geographic Cartesian reference frame is \( (O_{c} X_{c} Y_{c} Z_{c} ) \) and \( (O_{e} X_{e} Y_{e} Z_{e} ) \) respectively. \( \theta \) is the pitching angle of UCAV, \( \varphi \) represents the angle between UAV velocity and velocity projection. Then, the transformation matrix from \( (O_{e} X_{e} Y_{e} Z_{e} ) \) to \( (O_{c} X_{c} Y_{c} Z_{c} ) \) is:
The arbitrary position \( P_{c} \) of UCAV in the constrained reference frame is expressed by formula:
When the UCAV needs to be climb or descend to achieve its mission, there will be a maximum acceleration due to normal overload and radial overload. According to formula in [13] and [10], the UCAV maximum acceleration is:
where \( n_{f} \) and \( n_{g} \) are the normal overload and radial overload that UAV can withstand. \( g \) gravitational acceleration.
Adopting constant acceleration (CA) control strategy, the motion state of UCAV can be expressed as:
where \( p_{u,t} \), \( v_{u,t} \), \( a_{u,t} \) represents the position, velocity, and acceleration of the UCAV. Additionally, \( \Phi _{CA} \) is:
where \( \tau \) is the sampling cycle, \( {\mathbf{I}} \) is the third-order unit matrix, and 0 is the third-order zero matrix.
The maximum flight speed is a key factor in the UCAV flight process. In the acceleration process, in order to ensure the safety of UCAV during flight, UCAV cannot exceed its maximum sustainable speed, assuming that the maximum speed of UCAV is \( v_{\hbox{max} } \), the flight speed must satisfy the constraint:
Rewards
In the process of UCAV tracking target, we use the distance between UCAV and enemy target as the size of reward. When the distance between the two is less than the threshold we set, the reward will gradually increase, otherwise, will be given a negative reward.
where \( p_{a,t} \) and \( p_{u,t} \) represents UCAV and target location respectively.
3 Deep Reinforcement Learning
Reinforcement learning is a kind of method in machine learning and artificial intelligence. It studies how to achieve a specific goal through a series of sequential decisions. The process of reinforcement learning is realized through Markov Decision Making (MDP), it can be defined by the tuple \( (S,A,p,r) \), where the state space \( S \) and the action space \( A \), and the state transition probability \( p(s^{\prime}|s,a) \) represents the probability density of the next state \( s_{t + 1} \in S \) given the current state \( s \in S \) and action \( a_{t} \in A \). The environment emits a bounded reward \( r:S \times A \to [r_{\hbox{min} } ,r_{\hbox{max} } ] \) on each transition. The state transition process can be represented in Fig. 5.
When the agent’s actions are continuous or high dimensional, traditional reinforcement learning is difficult to deal with. DRL combines high-dimensional input of deep learning with reinforcement learning.
Standard RL maximizes the expected sum of rewards \( \sum\nolimits_{t} {E_{{(s_{t} ,a_{t} )\sim\rho_{\pi } }} } [r(s_{t} ,a_{t} )] \), soft actor-critic (SAC) requires actors to maximize the entropy of expectation and strategy distribution at the same time.
The temperature parameter \( \alpha \) determines the relative importance of the entropy term against the reward.
SAC incorporates three key factors:
-
(1)
An actor-critic structure consists of a separated policy and a value function network, in which the policy network is random;
-
(2)
An off-policy updating method, which updates parameters based on historical experience samples more efficiency;
-
(3)
Entropy maximization to ensure stability and exploratory ability.
Because SAC algorithm adopts above three points, it achieves state-of-the-art results on a series of continuous control benchmarks.
4 Simulated Experiment and Results
As mentioned before, we propose a continuous control optimization for moving target tracking based on soft actor-critic. In this section, we will discuss simulation results of the moving target tracking model. A total of 10000 iterations training were performed using a computer with a NVIDIA GeForce GTX 970M GPU card and 8G RAM in Explorer. Table 1 summarizes the parameter in the numerical simulations. For DRL, parameter setting has a greater impact on the results, and the super parameters need to be adjusted carefully. The SAC parameters used in the simulation experiments are listed in Table 2.
In this paper, to evaluate the performance of SAC algorithm in moving target tracking mission in Explorer. We set up four different difficulties missions, each difficult task is executed with 10000 episodes, and each episode has a tracking time of 400 s. Obviously, as the operation cycle decreases, the task becomes more difficult. At the beginning of each episode, UCAV and the location of the target are randomly reset. The maximum steps and operating cycles of UCAV with different difficulty are shown in Table 3.
4.1 Reward Analysis
To test the performance of missions on Explore at different difficulty levels, the mission completion is measured according to the mean accumulated reward (MAR), and the calculation formula is:
where \( ep \) represents the size of dividing the total steps of UCAV training. In order to more intuitively observe the performance of the algorithm, In the simulation, we set it to 40, \( R_{e} \) means the reward of UCAV in each step.
The simulation results of our system for different difficult missions are shown in Fig. 6.
By comparing the simulation diagrams of different difficult missions, we observed that UCAV performs poorly at the beginning of the missions and get the same rewards as adopting random policy. But when it learning a certain number of steps, the UCAV can get a reward close to 1, and the success rate of target tracking increases gradually.
4.2 Behavior Analysis
Although we can obtain from MAR that UCAV can track moving targets after a certain amount of training. In order to explain the flight situation of UCAV from different perspectives, we define the behavior angle (BHA) to describe the flight direction of UCAV:
where \( \vec{a}_{t} \), \( \vec{n}_{t} \) represents the target and UCAV flight direction respectively. For analysis convenience, \( \theta \) can be normalized into: \( \bar{\theta } = {\theta \mathord{\left/ {\vphantom {\theta \pi }} \right. \kern-0pt} \pi } \), where \( \bar{\theta } \in [0,1] \), when \( \bar{\theta } < 0.5 \) can be considered that UCAV has a tendency to toward the target. In different difficult missions, UCAV’s behaviors are shown in Fig. 7.
As shown in Fig. 7, the BHA of UCAV after training is smaller than that using random strategy. which indicates that UCAV has a tendency towards the target after a certain number of steps of training. By comparing the game environments with different difficulty, the performance of UCAV gradually improves with the increase of the difficulty of the mission from the perspective of reward and behavior angle, which shows that the convergence of SAC algorithm is better in the more complex environment.
4.3 Trajectory Analysis
In order to see the UCAV and the target flight trajectory clearly, we chose an episode with an operating cycle of 0.4 s. UCAV and target flight trajectory as shown in Fig. 8.
As shown in Fig. 8, the UCAV’s maneuvers at different time have different purposes. During the early operating cycles of UCAV, it began to fly towards moving targets. With the increase of UCAV operating steps, UCAV plans to track moving target.
5 Conclusion
In this paper, we build a three-dimension UCAV flight model named Explorer and combining with the deep reinforcement learning theory, design the flight motion and reward of UCAV. Using SAC algorithm realizes the UCAV tracking moving targets. The experimental results also show that UCAV can successfully track the moving target of the enemy after the number of iterations reaches a certain number of steps. It has strong application value in the field of cognitive electronic warfare.
References
Sutton, R.S., Barto, A.G.: Reinforcement Learning: An Introduction. MIT Press, Cambridge (1998)
Niu, C.F., Liu, Y.S.: Hierarchic particle swarm optimization based target tracking. In: International Conference on Advanced Computer Theory and Engineering, Cairo, Egypt, pp. 517–524 (2009)
Mu, C., Yuan, Z., Song, J., et al.: A new approach to track moving target with improved mean shift algorithm and Kalman filter. In: International Conference on Intelligent Human-machine Systems and Cybernetics (2012)
Hui, Z., Weng, X., Fu, Y., et al.: Study on fusion tracking algorithm of fire calculation for MMW/Tv combined guidance UCAV based on IMM-PF. In: Chinese Control and Decision Conference. IEEE (2011)
Wu, C., Han, C., Sun, Z.: A new nonlinear filtering method for ballistic target tracking. In: 2009 12th International Conference on Information Fusion. IEEE (2009)
Sun, T., He, B., Nian, R., et al.: Target following for an autonomous underwater vehicle using regularized ELM-based reinforcement learning. In: OCEANS 2015 - MTS/IEEE Washington. IEEE (2015)
You, S., Diao, M., Gao, L.: Deep reinforcement learning for target searching in cognitive electronic warfare. IEEE Access 7, 37432–37447 (2019)
Zhu, L., Cheng, X., Yuan, F.G.: A 3D collision avoidance strategy for UAV with physical constraints. Measurement 77, 40–49 (2016)
Haarnoja, T., Zhou, A., Abbeel, P., et al.: Soft actor-critic: off-policy maximum entropy deep reinforcement learning with a stochastic actor (2018)
Imanberdiyev, N., Fu, C., Kayacan, E., et al.: Autonomous navigation of UAV by using real-time model-based reinforcement learning. In: International Conference on Control. IEEE (2017)
You, S., Gao, L., Diao, M.: Real-time path planning based on the situation space of UCAVs in a dynamic environment. Microgravity Sci. Technol. 30, 899–910 (2018)
Ma, X., Xia, L., Zhao, Q.: Air-combat strategy using deep Q-learning 3952–3957 (2018). https://doi.org/10.1109/cac.2018.8623434
Dionisio-Ortega, S., Rojas-Perez, L.O., Martinez-Carranza, J., et al.: A deep learning approach towards autonomous flight in forest environments. In: 2018 International Conference on Electronics, Communications and Computers (CONIELECOMP). IEEE (2018)
Yun, S., Choi, J., Yoo, Y., et al.: Action-driven visual object tracking with deep reinforcement learning. IEEE Trans. Neural Netw. Learn. Syst. 29, 2239–2252 (2018)
Acknowledgment
This paper is funded by the International Exchange Program of Harbin Engineering University for Innovation-oriented Talents Cultivation.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Chen, T., Ma, X., You, S., Zhang, X. (2019). Soft Actor-Critic-Based Continuous Control Optimization for Moving Target Tracking. In: Zhao, Y., Barnes, N., Chen, B., Westermann, R., Kong, X., Lin, C. (eds) Image and Graphics. ICIG 2019. Lecture Notes in Computer Science(), vol 11902. Springer, Cham. https://doi.org/10.1007/978-3-030-34110-7_53
Download citation
DOI: https://doi.org/10.1007/978-3-030-34110-7_53
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34109-1
Online ISBN: 978-3-030-34110-7
eBook Packages: Computer ScienceComputer Science (R0)