Keywords

1 Introduction

In recent years, there has been significant interest in the paradigm of compressive sensing (CS) [1, 2], which is an emerging technique for sparse or compressible signals. A small amount of measurement data can be obtained by using linear random projecting, and then the signal can be reconstructed with high probability by the non-linear optimization. To achieve the perfect reconstruction, some block-based compressive sensing (BCS) methods have been proposed [3,4,5,6,7], which usually utilize the BCS smoothed projected Landweber (BCS-SPL) algorithm to reconstruct an original image [8].

Many literatures assume that the measurement process is effectuated within the sensing device, wherein lower-dimensional measurements are obtained with respect to high-dimensional data. Accordingly, the measurement process can be regarded as conducting data acquisition and data compression simultaneously. However, the measurement process does not bring a real compression in the strict information theoretic sense, because it cannot produce a bitstream from the sensing device directly, which only can be seen as a technology of dimensionality reduction in essence [9]. The real compressive sensing is the process that produces an ultimate compressed bitstream from the input data, which needs to be cooperated with quantization and entropy coding modules. Without effective quantization process, the image compressive sensing is found inefficient in rate-distortion performance [10]. As a result, much attention has been devoted to the improvement of rate-distortion performance of quantized compressive sensing [11,12,13], which appears very complicated and is not applicable to the BCS framework. Therefore, one straightforward solution is to simply apply the scalar quantization (SQ) to the measurements acquired by the sensing device.

Inspired by the success of the block-based hybrid video coding, the intra prediction coding technology can be also used in the BCS measurement process. Mun and Fowler [14] proposed the block-based quantized compressive sensing of natural images with differential pulse-code modulation (DPCM), coupled with uniform scalar quantization, where the previous reconstructed measurement is taken as the candidate of the current measurement and subtracted from the current measurement. Instead of applying quantization directly to each block of BCS measurements, the resulting residual is then scalar-quantized. The simple DPCM-plus-SQ method provides surprisingly competitive rate-distortion performance. However, it is not efficient enough to leverage previous measurement as the prediction of the current measurement, because the non-stationarity of natural images is ignored. Zhang et al. [15] extended the DPCM-based BCS measurement coding and proposed the spatially directional predictive coding (SDPC), where the intrinsic spatial correlation between neighboring measurements of natural images are further explored. For each compressive sensing block, the optimal measurement prediction is selected from a set of multiple measurement prediction candidates, which are generated by four directional prediction modes. Unlike SDPC, Li et al. [16] introduced a median filter predictive quantization (MFPQ) method and took the median of several reconstructed adjacent blocks around the current measurement as the optimal measurement prediction of the current measurement. Although the R-D performance is slightly lower than that of SDPC, the computational complexity of MFPQ is also lower than that of SDPC, and better error resilience is achieved. Compared with DPCM, the SDPC method obtains accurate measurement prediction with better rate-distortion performance, but it also increases computational complexity. Another problem is that Refs. [15, 16] are affected by image edge. For the measurements of image edge, only the measurements from their vertical direction, that is, the previous measurement is effectively utilized. What’s more, the existing methods only consider the measurement-domain prediction of maximum four directional modes, not all possible directional modes. In theory, there are eight directional modes in the current measurement. Zhou et al. [17] further proposed an angular measurement intra prediction with compressive sensing, and designed more structural rows in random measurement matrix for embedding more accurate adjacent boundary information, but it requires far large computation due to its pixel-based operation.

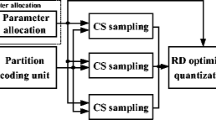
To overcome the shortcomings of the aforementioned methods, this paper proposes a measurement-domain spiral predictive coding (SPC) method. The proposed SPC-plus-SQ method starts from the central block of an image and continues to predict the next block in spiral scanning order. For each current measurement, the optimal measurement prediction is selected from a set of multiple measurement prediction candidates generated by at most eight direction prediction modes, which is more accurate than the aforementioned methods. The proposed SPC-plus-SQ method is not affected by image edge simultaneously. This process is shown in Fig. 1, and the experimental results will verify that the proposed method can achieve the best rate-distortion performance as compared with the SQ alone, DPCM-plus-SQ, SDPC-plus-SQ and MFPQ-plus-SQ methods. In addition, its computational complexity is also almost similar with the SDPC-plus-SQ method.

Fig. 1.
figure 1

Architecture of SPC-plus-SQ for block-based compressive sensing (BCS). SQ is uniform scalar quantizer; SQ−1 is inverse uniform scalar quantizer; P is the proposed spiral directional predictive coding module; C is an entropy encoder; BCS-SPL is an image reconstruction module.

Full size image

This paper is organized as follows. Section 2 briefly reviews the BCS framework. The details of proposed method are given in Sect. 3. Experimental results are shown in Sect. 4, and conclusions are drawn in Sect. 5.

2 The BCS Framework

For real signal \( y \in \Re^{N} \), if it is \( k \)-sparse in orthogonal transformation domain \( \Psi \), then

$$ {\text{y}} = \Psi\uptheta $$
(1)

where \( \uptheta \) is a sparse coefficient vector, and real signal \( {\text{y}} \) is sparse under the domain Ψ. The measurement matrix \( \Phi = \left[ {\varphi_{1}^{T} ,\varphi_{2}^{T} , \ldots \varphi_{i}^{T} , \ldots ,\varphi_{M}^{T} } \right] \) is used to measure the signal \( {\text{y}} \) and the measurement vector \( {\text{x}} \in {\Re }^{M} \) is obtained, where \( \varphi_{i}^{T} \in \Re^{N} \) is the row vector, \( k < M \ll N \). Then, the measurement equation can be expressed as

$$ \text{x} = \Phi {\text{y}} $$
(2)

where the signal \( {\text{x}} \) can be reconstructed accurately by the non-linear optimization calculation.

In order to avoid the large storage cost of measurement matrix and the rapid increase of sampling/recovery complexity as the size of sensing signal increases in compressive imaging, a BCS framework of 2D image was proposed, wherein the sampling of an image is driven by random matrices applied on a block-by-block basis. That is, an image \( {\text{y}} \) is firstly divided into \( n \) non-overlapped blocks of size \( B \times B \) with each block denoted by \( {\text{y}}^{\left( i \right)} \in {\Re }^{{B^{2} }} ,i = 1,2, \ldots ,n \) in vector representation along the vertical or horizontal scan order. Then, its corresponding measurement \( {\text{x}}^{\left( i \right)} \) is obtained by

$$ {\text{x}}^{\left( i \right)} = \Phi_{B} \;{\text{y}}^{\left( i \right)} $$
(3)

where \( x^{\left( i \right)} \in \Re^{{M_{B} }} \) and \( \Phi_{B} \) is an \( M_{B} \times B^{2} \) measurement matrix such that the subrate for the image as a whole remains \( S = M_{B} /B^{2} . \) It is straightforward to conclude that \( \Phi_{B} \) applied to an image at block level is equivalent to a whole image measurement matrix \( \Phi \) with a constrained structure, namely, \( \Phi \) can be written as a block diagonal with \( \Phi_{B} \) along the diagonal.

3 Spiral Predictive Coding

In an image, each block is not independent with each other, and they have certain spatial correlation with the surrounding blocks. Therefore, it can be inferred that each BCS measurement has some spatial correlation with the measurements around it. Further, Because of the non-stationarity of natural image, correlation coefficients of a measurement are different with its adjacent measurements in different directions. The optimal measurement prediction should be selected from the adjacent reconstructed measurements set for the current measurement. Actually, if the current measurement has more measurement prediction candidates to be chosen, the optimal measurement prediction is closer to the current measurement. This is basic idea of spiral prediction coding for BCS. The details are as given below.

As shown in Fig. 1, an input natural image \( {\text{y}} \) is first divided into n non-overlapping blocks, and the block size is \( B \times B \), and each block is denoted by \( y^{\left( i \right)} \in \Re^{{B^{2} }} ,i = 1,2, \ldots ,n \) in vector. The proposed method is that the first block begins in the center of the image, which is denoted by \( y^{{\left( {n/2} \right)}} \) and is sampled by the BCS measurement matrix in spiral scanning order. Then, all BCS measurements are acquired by Eq. (3). Next, for measurements which have just been acquired by BCS measurement matrix, each measurement is denoted by \( {\text{x}}^{\left( i \right)} \in {\Re }^{{M_{B} }} ,i = 1,2, \ldots ,n \) in vector. The proposed method fully considers all eight directional prediction modes from its neighboring BCS measurement which have already been reconstructed, namely, up, up-right, up-left, right, left, down, down-right, and down-right. More specially, let \( \tilde{x}_{A}^{\left( i \right)} \), \( \tilde{x}_{B}^{\left( i \right)} \), \( \tilde{x}_{C}^{\left( i \right)} \tilde{x}_{D}^{\left( i \right)} \), \( \tilde{x}_{E}^{\left( i \right)} \), \( \tilde{x}_{F}^{\left( i \right)} \), \( \tilde{x}_{G}^{\left( i \right)} \), and \( \tilde{x}_{H}^{\left( i \right)} \) denote the up, up-right, up-left, right, left, down, down-right, and down-right blocks of measurements with regard to \( {\text{x}}^{\left( i \right)} \) respectively, as illustrated in Fig. 2.

Fig. 2.
figure 2

The proposed eight directional predictive modes and eight corresponding predicted measurement blocks with respect to current measurement block \( {\text{x}}^{\left( i \right)} \) from its neighboring measurement blocks.

Full size image

It is worth noting that the deficiency of the SDPC-plus-SQ method is that there are fewer spatial direction measurement predictions for the blocks of image edge, usually only the previous measurement prediction. The proposed method starts from the center block and proceeds in the spiral scanning order. Even in the edge blocks of the image, there are more spatial direction measurement predictions to be chosen. Furthermore, the proposed method takes into all-direction measurement predictions around current measurement as the measurement prediction candidates set. Therefore, the proposed method may perform better than the existing methods.

Here defines a set of measurement prediction candidates as follow:

$$ R = \left\{ {\tilde{x}_{A}^{\left( i \right)} , \tilde{x}_{B}^{\left( i \right)} ,\tilde{x}_{C}^{\left( i \right)} \tilde{x}_{D}^{\left( i \right)} ,\tilde{x}_{E}^{\left( i \right)} ,\tilde{x}_{F}^{\left( i \right)} ,\tilde{x}_{G}^{\left( i \right)} ,\tilde{x}_{H}^{\left( i \right)} } \right\} $$
(4)

where \( R \) is a collection of above eight directional prediction modes. The measurement prediction candidates in the sets are reconstructed measurements of previously non-overlapped blocks. For the current measurement, the optimal measurement prediction denoted by \( \hat{x}_{P}^{\left( i \right)} \), is determined by minimizing the residual between the current measurement \( {\text{x}}^{\left( i \right)} \) and the measurement prediction candidates in the sets.

$$ \hat{x}_{P}^{\left( i \right)} = \arg \mathop {\hbox{min} }\limits_{x \in R} \left\| {x - {\text{x}}^{\left( i \right)} } \right\|_{{\ell_{1} }} $$
(5)

Here, \( \left\| * \right\|_{{\ell_{1} }} \) is \( \ell_{1} \) norm which adds all the absolute values of the entries in a vector.

After obtaining the optimal measurement prediction \( \hat{x}_{P}^{\left( i \right)} \), the residual can be calculated by \( d^{\left( i \right)} = {\text{x}}^{\left( i \right)} - \hat{x}_{P}^{\left( i \right)} \). Following, the residual \( d^{\left( i \right)} \) is quantized by a uniform scalar quantization with quantization step q to obtain the quantization index \( s^{\left( i \right)} \).

$$ s^{\left( i \right)} = {\mathcal{Q}}\left[ {d^{\left( i \right)} } \right] $$
(6)

Then, the quantization index \( s^{\left( i \right)} \) is encoded by the entropy encoder to further reduce its statistical redundancy and transmitted to the decoder at the receiver. Continue to the encoder, the quantized residual \( d^{\left( i \right)} \) is obtained by inverse quantization of the quantization index \( s^{\left( i \right)} \), then residual \( d^{\left( i \right)} \) is added to the optimal measurement prediction \( \hat{x}_{P}^{\left( i \right)} \) just obtained, and the sum is used as the measurement prediction candidate of the adjacent direction mode for the next measurement.

The bitstream to be transmitted in Fig. 1 consists of two parts: the standard bits of the best prediction direction mode which is used to inform the decoder of the selected measurements prediction and the bitstream data obtained by encoding the quantization index \( s^{\left( i \right)} \) with the entropy encoder. This process is applied for all BCS measurements to achieve the final bitstream.

At the decoder side, contrary to the above encoding process, by the de-quantization on the quantization index from the bitstream, the quantized residuals \( \tilde{d}^{\left( i \right)} \) can be obtained, which is then added by the prediction \( \hat{x}_{P}^{\left( i \right)} \), producing the CS measurements \( \tilde{x}^{\left( i \right)} = \hat{x}_{P}^{\left( i \right)} + \tilde{d}^{\left( i \right)} \). At last, all groups of reconstructed measurements \( \tilde{x} \) are obtained sequentially, which are then utilized for the natural image reconstruction by using the BCS-SPL reconstruction algorithm.

In order to demonstrate the superiority of the proposed method, a correlation coefficient \( \rho \) is used for quantitative comparison with DPCM, SDPC, and MFPQ.

$$ \rho \left( {X^{\left( i \right)} ,X^{\left( j \right)} } \right) = \frac{{X^{{\left( i \right)^{T} }} X^{\left( j \right)} }}{{\left\| {X^{\left( i \right)} } \right\|\left\| {X^{\left( j \right)} } \right\|}} $$
(7)

The correlation coefficients can measure and compare the measurement vectors of current measurements and their optimal measurement predictions. For each current measurement, the MFPQ method computes the median value of components in measurement vectors of neighboring measurements as the optimal measurement prediction, the DPCM method uses directly previous measurement as the optimal measurement prediction, and the SDPC method selects the optimal measurement prediction from four directional modes by using the least square error criterion. The proposed method is similar to the SDPC method, selecting the optimal measurement prediction from eight directional modes, but the proposed method is not affected by image edges because of the spiral scanning order. In theory, the proposed method can get the most accurate measurement prediction in these methods due to more measurement prediction candidates to be chosen. It can be verified by Table 1 which presents the average correlation coefficients of DPCM, SDPC, MFPQ and SPC. The correlation coefficients are calculated by Eq. (7) over all 16 × 16 blocks for three 512 × 512 test images with different sampling rates. There is no doubt that the maximum average correlation coefficients are obtained by the proposed method in all methods.

Table 1. Average correlation coefficients for various methods in measurement domain
Full size table

It is worth noting that, as shown in the Table 2, although the proposed method achieves the maximum correlation coefficient among these prediction methods, the computational complexity is even slightly lower than that of SDPC. The computational complexity of MFPQ and DPCM is lower than the proposed method, but their average correlation coefficient is much lower, which will affect the quality of image reconstruction.

Table 2. Computational complexity of different prediction methods for each block (M denotes the length of measurement vector of each block)
Full size table

4 Experimental Results

The experimental results are provided to verify the performance of the proposed method. The rate-distortion efficiency of the proposed SPC-plus-SQ method is examined by comparing it to SDPC-plus-SQ, DPCM-plus-SQ, MFPQ-plus-SQ and SQ alone applied to BCS measurements. The BCS-SPL algorithm is always exploited to reconstruct the decoded measurements by the above five prediction methods.

In the implementations, two grayscale test images are 512 × 512 pixels, the block size for BCS is typically set to be 16 × 16 and the measurement matrix \( \Phi_{B} \) is an orthogonal random Gaussian matrix. Image quality is evaluated by means of the rate-distortion performance in terms of peak signal-to-noise ratio (PSNR) in dB at different bitrates in bits per pixel (bpp). The actual bitrate is estimated by the entropy of the quantizer indices, which would be actually produced by a real entropy coder. The setup of the combination of step-size and subrate is the same as that in Refs. [14,15,16].

Tables 3 and 4 respectively give the PSNR results of two images (namely Lenna and Peppers) at various bitrates (from 0.6 bpp to 1.6 bpp) under the BCS-SPL algorithm, coupled with five prediction & coding techniques, namely, SQ alone, DPCM-plus-SQ, SDPC-plus-SQ, MFPQ-plus-SQ and SPC-plus-SQ. One easily observes that, the proposed method obtains the best PSNR performance among five methods, and it improves 0.18 dB gain in the first test image and 0.12 dB gain in the second test image on average PSNR as compared to SDPC-plus-SQ relatively, which can demonstrate the superiority of the proposed SPC.

Table 3. PSNR (dB) comparison for five methods on the image Lenna
Full size table
Table 4. PSNR (dB) comparison for five methods on the image Peppers
Full size table

5 Conclusion

A new measurement-domain spiral predictive coding is proposed, which can make full use of the intrinsic spatial relationship of natural images and is not affected by image edges. The direction prediction block in the proposed method starts from the center of an image and spreads around in spiral scanning, where each measurement-domain block can select the optimal measurement prediction from the candidates set as many as possible. The experimental results show that the proposed SPC-plus-SQ method can achieve the best rate-distortion performance as compared with the existing methods.