Abstract
In this work, we propose a novel hybrid Fourier-transform phase-shifting profilometry method to integrate the advantages of Fourier-transform profilometry (FTP) and phase-shifting profilometry (PSP). The motion vulnerability of multi-shot PSP can be significantly alleviated through the combination of single-shot FTP, while the high accuracy of PSP can also be preserved when the object is motionless. We design a phase-based pixel-wise motion detection strategy that can accurately outline the moving object regions from their motionless counterparts. The final measurement result is obtained by fusing the determined regions where the PSP or FTP is applied correspondingly. To validate the proposed hybrid approach, we develop a real-time 3D shape measurement system for measuring multiple isolated moving objects. Experimental results demonstrate that our method achieves significantly higher precision and better robustness compared with conventional approaches where PSP or FTP is applied separately.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The fringe projection profilometry (FPP) [1, 2] is one of the most popular three-dimensional (3D) surface measurement technologies due to its advantages in terms of high measurement accuracy, simple hardware configuration, and being easy to implement. With the recent advances in high speed imaging sensors and digital projection technology, it now becomes possible to achieve high-precision, high-speed real-time 3D shape measurement of dynamic scenes [3].
The phase-shifting profilometry (PSP) [4, 5] and Fourier-transform profilometry (FTP) [6] are two mainstream fringe analysis approaches of FPP. FTP retrieves phase information from only one single high-frequency fringe image, so it is well-suited for dynamic 3D sensing [7]. However, the frequency band overlapping problem limits its measurement precision, which can be improved by the \(\pi \) phase-shifting FTP [8], modified FTP [9], or background normalized FTP [10]. On the other hand, PSP typically requires a minimum of three fringe images to provide high-accuracy pixel-wise phase measurement, the advantages of which are higher spatial resolution, measurement accuracy, and robustness towards ambient illumination and varying surface reflectivity [11, 12]. However, when measuring dynamic scenes, motion will lead to phase distortion artifacts and make the accuracy of PSP lower than that of FTP, that is an intrinsic and inevitable problem of PSP.
During recent years, dynamic 3D shape measurement using FPP has attracted a great deal of research interest, which can be roughly categorized in the following three directions: (1) Increasing the speed of hardware (projector and camera); (2) Reducing the number of required patterns per 3D reconstruction; (3) Improving the measurement quality and reducing the motion artifacts. The first direction focuses on the projector defocusing technique that allows the projector to cast binary fringe patterns close to the sinusoidal ones to maximize the speed of the projector [10, 13]. When the high-speed projector is synchronized with a high-speed camera, motion-induced error on the phase reconstruction can be reduced accordingly, depending on the frame rate of the projector-camera pair. The second direction is to improve the measurement efficiency, i.e., to reduce the number of patterns required per measurement. Essentially, the dominant challenge affecting the measurement efficiency is the phase ambiguity. To recover the absolute phase, a common practice is to use temporal phase unwrapping (TPU) algorithm [14, 15]. However, additional multi-wavelength fringes should be used in TPU, which decreases the measurement efficiency. Recently, stereo phase unwrapping (SPU) methods based on geometric constraint [16] can be used to solve the phase ambiguity problem without using additional auxiliary patterns [17,18,19], which is well-suitable to high-speed real-time 3D shape measurement of dynamic scenes. The third direction focuses on enhancing the dynamic measurement capability of PSP with use of post-processing algorithm. These motion compensation methods [17, 20,21,22,23,24] can improve the accuracy of PSP in dynamic scenes to some extent. However, most of them adopt iterative methods, which makes the computational efficiency relatively low, and some other methods are restricted to certain assumptions and are not suitable for non-rigid motion compensation. In addition, Yang et al. [25] proposed the methods of combining single-frame method and multi-frame method, where the motion regions of the object are detected, and different imaging methods are used according to different regions. In contrast to other methods, the method is more targeted, i.e., the motion compensation algorithm is only performed in the motion regions, while the high precision of multi-frame method in the still regions is preserved. However, only local rather than pixel-by-pixel motion state can be judged by this method, because this method is susceptible to ambient light noise.
The goal of this paper is to develop a new 3D shape measurement technique which can measure 3D shapes robustly in real time for rigid and non-rigid objects in complex scenes consisting of both static and dynamic objects. To this end, we propose a novel hybrid Fourier-transform phase-shifting profilometry method for motion-induced error reduction. First of all, four patterns are projected onto the objects, from which the absolute phase information can be simultaneously calculated by both PSP and FTP. Then, the motion regions of the measured objects are automatically detected with a pixel-wise motion detection strategy based on phase information. At last, the results of PSP and FTP are fused according to the detected motion regions. In order to prove the feasibility of the proposed method, a real-time 3D shape measurement system based on our method is developed. Experiments show that our method can integrate the advantages of PSP and FTP to achieve higher measurement precision than traditional real-time algorithms based on PSP or FTP.
2 Principle
2.1 Basic Principles of 3-Step PSP and SPU
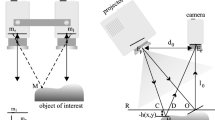
A typical 3D imaging system based on SPU is composed of two cameras and one projector [18]. Taking three-step phase-shifting fringe patterns for example, the patterns captured by the camera can be expressed by the following formulas:
where the superscript c denotes the camera, \(({u^c},{v^c})\) is a point in the camera, \(I_1^c\), \(I_2^c\) and \(I_3^c\) represent the three captured fringe patterns, \(A^c\) is the average intensity map, \(B^c\) is the amplitude intensity map, and \({\varPhi ^c}\) is the absolute phase map. Because of the truncation feature of the arctan function, only the wrapped phase can be obtained with Eqs. (1)–(3):
where \({\phi ^c}\) represents the wrapped phase. The absolute phase map and the wrapped phase map satisfy the following relation:
where \(k^c\) is the fringe order, and N denotes the number of fringes. The process of obtaining the fringe orders is called phase unwrapping.
The principle of SPU is shown in Fig. 1. For an arbitrary point \({o^{{c_1}}}\) in the Camera 1, it has N possible fringe orders corresponding to N possible absolute phases, with which the horizontal coordinates of the corresponding points in the projector can be obtained. Then the N corresponding 3D candidates can be retrieved by the parameter matrices derived from calibration parameters between the Camera 1 and the projector. The retrieved N 3D candidates can be projected into the Camera 2 to get their corresponding 2D candidates just like the red and green points in the Camera 2 in Fig. 1. There is a correct matching point which should have the more similar wrapped phase to \({o^{{c_1}}}\) among these 2D candidates. Then a phase similarity check will be carried out to find the matching point, and the phase ambiguity of \({o^{{c_1}}}\) will also be removed.
However, conventional SPU is not enough to robustly eliminate phase ambiguities when high-frequency fringes are used. Depth constraint [16, 19] is a popular method to improve the stability of SPU. The strategy of adaptive depth constraint (ADC) proposed by Tao et al. [18] can provide and update the pixel-wise depth range automatically according to the real-time measurement results, which is especially suitable for the measurement where the object is moving constantly. So, in this work, we utilize this method to assist SPU to improve the stability of the measurement.
Although PSP based on SPU can robustly remove phase ambiguity in the static scene, the motion-caused phase error and unwrapping error in motion introduced scene make it necessary to compensate for the motion-induced error of PSP.
2.2 Composite Phase Retrieval Method Based on FTP and PSP
To reduce the sensitivity to motion, PSP with as few fringe patterns as possible should be applied. Therefore, three-step phase-shifting method is chosen in this work. We use the second fringe of the three-step phase-shifting images to perform FTP. Meanwhile, in order to improve the measurement precision of FTP, we use the background-normalized Fourier transform profilometery (BNFTP) [10], where a pure white map is cast the light intensity of which is equal to the average intensity of the three-step phase-shifting fringes. By taking the normalized difference between \(I_2^c\) and the average intensity, the zero-frequency term as well as the effect of surface reflectivity variations can be effectively removed before the Fourier transform. Considering both the efficiency of PSP and the precision of FTP, the fringe strategy selected in this work is a 1 + 3 strategy which is one pure white map and three three-step phase-shifting fringe patterns.
The entire algorithm process is discussed next. Firstly, the wrapped phases are respectively calculated by PSP and FTP. SPU is implemented to achieve phase unwrapping of the FTP phase with the assistance of ADC, while the ambiguity of the wrapped phase of PSP is removed by means of the absolute FTP phase. Then, the matching points of the Camera 1 of PSP and FTP can be respectively obtained. Finally, the results of PSP and FTP are fused by the determined motion regions of the object. For the still regions, the result of PSP is reserved, while the result of the motion regions, is replaced with that of FTP. The whole algorithm flow is shown in Fig. 2.
The steps of the whole algorithm are summarized as follows:
-
\(Step\ 1\): Obtain the wrapped phases by PSP and FTP respectively;
-
\(Step\ 2\): Unwrap the wrapped phase of FTP by SPU, with the assistance of ADC;
-
\(Step\ 3\): Unwrap the wrapped phase of PSP by means of the absolute phase of FTP;
-
\(Step\ 4\): Obtain the matching points of the Camera 1 of PSP and FTP respectively;
-
\(Step\ 5\): Fuse the matching points of PSP and FTP with the detected motion areas and achieve 3D reconstruction;
-
\(Step\ 6\): Update the range of the next cyclic dynamic depth constraint with the obtained depth information;
-
\(Step\ 7\): Return back to \(Step\ 1\) and repeat the above process;
3 Motion Detection and Judgment
The key to the proposed algorithm is how to analyze the state of motion of the object pixel by pixel. In this paper, we propose the phase frame different method (PFDM), which is a motion detection method based on phase differentials from frame to frame. Firstly, the absolute value of the phase difference introduced by motion between the FTP phases of two adjacent moments is calculated. Then, the phase change of each point is compared with a certain threshold. If the phase change is greater than the threshold, it is considered to be in motion and the corresponding point of the output motion state map is 1, otherwise judged to be stationary and the corresponding output is 0. In order to eliminate some individual stationary points judged to be moving and to correct some individual undetermined motion points, we perform Gaussian filtering on the output motion state map. After filtering, if the output of a certain point is less than 1/2, it is considered to be stationary, otherwise judged to be in motion.
In order to accurately determine the motion regions, the threshold of motion judgment needs to be reasonably designed. The process of the determination of the threshold is as shown in Fig. 3. Firstly, we measure a flat panel in a static environment and obtain its absolute phase. We record the phase values of a fixed area as shown by the red dashed box in Fig. 3 of successive n moments \({t_0} \sim {t_{n - 1}}\), and then sum and average them. The resulting average phase can be approximated as the phase value measured without ambient light noise. Then the histogram of the difference between the average phase and the phase at time \({t_{n - 1}}\) is obtained. Areas with a value of less than e in the histogram are removed, such as the red areas of the histogram in Fig. 3, and then the two areas with the greatest difference are acquired, such as the green ones of the histogram in Fig. 3. Here e represents a smaller constant, which is 10 in this work. The absolute values are obtained for these two regions, and the upper limit of the larger region is taken as the phase threshold.
4 Experiment
We establishe a quad-camera real-time 3D imaging system based on the proposed method, which is shown in Fig. 4, where Fig. 4(a) is the outline structure, and Fig. 4(b) is the internal structure. This set-up includes a LightCrafter 4500Pro (\(912 \times 1140\) resolution), three Basler acA640-750um cameras (\(640 \times 480\) resolution) used for SPU and one Basler acA640-750uc camera (\(640 \times 480\) resolution) used for colorful texture. In our experiments, the projection speed is 100 Hz, and all the cameras are synchronized by the trigger signal from the projector and 48-period phase-shifting fringe patterns are used.
4.1 Comparison of Two Methods of Motion Judgment
In the first experiment, two different scenes are designed to compare the performance of PFDM and the Yang’s method [25] which is frame difference method (FDM). In the first scene, a rigid object is measured in the first scene as shown in Fig. 5(a). The measurement results are shown Figs. 5(b)–(c). These results indicate that PFDM performs better than FDM in judging the motion of rigid object. In the second scene, a freely moving hand is measured as shown in Fig. 5(d). Figures 5(e)–(f) display the motion regions detected by FDM and PFDM. Obviously, for the motion of non-rigid objects, the detection accuracy of PFDM is still better than that of FDM.
The motion regions determined by FDM and PFDM. (a) The first measurement scene. (b) The result of FDM of the first scene (A rigid object in translational motion). (c) The result of PFDM of the first scene. (d) The second measurement scene (A hand in arbitrary motion). (e) The result of FDM of the second scene. (f) The result of PFDM of the second scene.
Measurement results in the second complex scenario. (a) The background map collected. (b) The detected motion areas. (c) The results measured by the conventional PSP. (e) The error distribution of the flat plate data of (c). (g)The histogram of (e). (d) The results measured by our method. (f) The error distribution of the flat plate data in (e). (h) The histogram of (f).
4.2 Quantitative Evaluation
In the second experiment, a rotating flat plate is measured. For the rotating object, the portion near the center of rotation can be considered to be stationary, and those on both sides of the center of rotation are moving, which presents two different motion states. The measurement results are shown in Fig. 6, where Fig. 6(a) is the background map, Fig. 6(b) is the detected motion areas, Figs. 6(c), (e) and (g) are the results measured by a real-time algorithm based on stereo phase unwrapping using only the PSP algorithm [19] (for simplicity, the method is hereinafter referred to as “traditional PSP”), and Figs. 6(d), (f) and (h) are those of the proposed method. The plane fittings on the measured plate data of a certain area, as shown in the area inside the red dotted frame in Fig. 6(a) are performed. Figures 6(e) and (f) are the errors between the measured data of the two methods and the fitted data and Figs. 6(g) and (h) are the histograms of Figs. 6(e) and (f), respectively. It can be seen from Fig. 6(b) that PFDM judges the center of the object rotation to be stationary, and the two sides of the center of the rotation are judged to be moving. The RMS of the measurement error of the conventional PSP is 89 um. The results measured by our method combine the results of PSP and FTP, in which the data in the red dashed box as shown in Fig. 6(f) is that of PSP while that of other region is the result of FTP. The RMS of the measurement error of our method is 40 um, which is better than that of the traditional PSP.
4.3 Qualitative Evaluation
In this experiment, a moving hand is measured, which is a non-rigid body with complex motion. Figure 7 shows the measured results, where Figs. 7(a) and (c) are the results of PSP and our method respectively, and Fig. 7(b) is the motion regions detected by PFDM. We can see from the measurement results that the proposed method can eliminate the motion-induced ripples of non-rigid object.
4.4 Real-Time Experiments
In the final experiment, the established quad-camera real-time 3D imaging system based on the proposed method is used to measure the small fan and David model in motion by conventional PSP and our method respectively. We use a HP Z230 computer (Intel Xeon E3-1226 v3 CPU, NVIDIA Quadro K2200 GPU). The visual interface is developed with Qt and all core algorithms are written based on CUDA. The real-time measurement results are shown in Fig. 8. It can be observed from the measurement results that for the motion regions, the results of PSP have obvious motion ripples, while those of our method have no motion ripples in which the results of PSP are replaced by those of FTP. About 30 fps reconstructed speed can be achieved by our method.
5 Conclusion
In this paper, we present a novel hybrid Fourier-transform phase-shifting profilometry method for rigid and non-rigid objects in the complex scenes which contain both static and dynamic motions. Firstly, we use a 1 + 3 fringe strategy to retrieve the phase information of the measured objects with both PSP and FTP assisted by ADC which can efficiently achieve phase unwrapping of the high frequency fringes. Then, we develop a phase-based motion detection strategy to accurately determine the motion state of each pixel. Finally, based on the detected regions of motion, we combine the results of PSP and FTP. Several experiments have verified that the proposed method can obtain more precise 3D reconstruction than traditional real-time strategy based on PSP or FTP. Compared to other motion-compensation methods such as Lu’s method [20], which can significantly eliminate the effects of 3D motion on PSP by redefining the motion-affected fringe pattern and the use of an iterative least-squares algorithm but is only applicable to a single movement of non-rigid objects, our approach is suitable for objects under both rigid and non-rigid motion, showing the higher feasibility for more kinds of scenes, and easier to implement.
References
Geng, J.: Structured-light 3D surface imaging: a tutorial. Adv. Opt. Photonics 3, 128–160 (2011)
Gorthi, S.S., Rastogi, P.: Fringe projection techniques: whither we are? Opt. Lasers Eng. 48, 133–140 (2010)
Zhang, S.: Recent progresses on real-time 3D shape measurement using digital fringe projection techniques. Opt. Lasers Eng. 48, 149–158 (2010)
Zuo, C., Feng, S., Huang, L., Tao, T., Yin, W., Chen, Q.: Phase shifting algorithms for fringe projection profilometry: a review. Opt. Lasers Eng. 109, 23–59 (2018)
Srinivasan, V., Liu, H.-C., Halioua, M.: Automated phase-measuring profilometry of 3-D diuse objects. Appl. Optics 23, 3105–3108 (1984)
Su, X., Zhang, Q.: Dynamic 3-D shape measurement method: a review. Opt. Lasers Eng. 48, 191–204 (2010)
Takeda, M., Ina, H., Kobayashi, S.: Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. JosA 72, 156–160 (1982)
Li, J., Su, X., Guo, L.: Improved fourier transform profilometry for the automatic measurement of three-dimensional object shapes. Opt. Eng. 29, 1439–1445 (1990)
Guo, H., Huang, P.S.: 3-D shape measurement by use of a modified fourier transform method. In: Proceedings of SPIE -International Society for Optical Engineering, vol. 7066 (2008)
Zuo, C., Tao, T., Feng, S., Huang, L., Asundi, A., Chen, Q.: Micro fourier transform profilometry (FTP): 3D shape measurement at 10,000 frames per second. Opt. Lasers Eng. 102, 70–91 (2018)
Li, J., Hassebrook, L.G., Guan, C.: Optimized two-frequency phase-measuring-profilometry light-sensor temporal-noise sensitivity. JOSA A 20, 106–115 (2003)
Su, X.-Y., Von Bally, G., Vukicevic, D.: Phase-stepping grating profilometry: utilization of intensity modulation analysis in complex objects evaluation. Opt. Commun. 98, 141–150 (1993)
Zhang, S., Van Der Weide, D., Oliver, J.: Superfast phase-shifting method for 3-D shape measurement. Opt. Express 18, 9684–9689 (2010)
Zuo, C., Huang, L., Zhang, M., Chen, Q., Asundi, A.: Temporal phase unwrapping algorithms for fringe projection profilometry: a comparative review. Opt. Lasers Eng. 85, 84–103 (2016)
Zhang, Z., Towers, C.E., Towers, D.P.: Time eÿcient color fringe projection system for 3D shape and color using optimum 3-frequency selection. Opt. Express 14, 6444–6455 (2006)
Bräuer-Burchardt, C., Munkelt, C., Heinze, M., Kühmstedt, P., Notni, G.: Using geometric constraints to solve the point correspondence problem in fringe projection based 3D measuring systems. In: Maino, G., Foresti, G.L. (eds.) ICIAP 2011. LNCS, vol. 6979, pp. 265–274. Springer, Heidelberg (2011). https://doi.org/10.1007/978-3-642-24088-1_28
Weise, T., Leibe, B., Van Gool, L.: Fast 3D scanning with automatic motion compensation. In: IEEE Conference on Computer Vision and Pattern Recognition. CVPR 2007, pp. 1–8. IEEE (2007)
Tao, T., et al.: High-speed real-time 3D shape measurement based on adaptive depth constraint. Opt. Express 26, 22440–22456 (2018)
Tao, T., Chen, Q., Feng, S., Hu, Y., Zhang, M., Zuo, C.: High-precision real-time 3D shape measurement based on a quad-camera system. J. Opt. 20, 014009 (2017)
Lu, L., Xi, J., Yu, Y., Guo, Q.: Improving the accuracy performance of phase-shifting profilometry for the measurement of objects in motion. Opt. Lett. 39, 6715–6718 (2014)
Feng, S., et al.: Robust dynamic 3-D measurements with motion-compensated phase-shifting profilometry. Opt. Lasers Eng. 103, 127–138 (2018)
Li, B., Liu, Z., Zhang, S.: Motion-induced error reduction by combining fourier transform profilometry with phase-shifting profilometry. Opt. Express 24, 23289–23303 (2016)
Cong, P., Xiong, Z., Zhang, Y., Zhao, S., Wu, F.: Accurate dynamic 3D sensing with fourier-assisted phase shifting. IEEE J. Sel. Top. Signal Process. 9, 396–408 (2015)
Liu, Z., Zibley, P.C., Zhang, S.: Motion-induced error compensation for phase shifting profilometry. Opt. Express 26, 12632–12637 (2018)
Yang, Z., Xiong, Z., Zhang, Y., Wang, J., Wu, F.: Depth acquisition from density modulated binary patterns. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 25–32 (2013)
Funding
National Natural Science Fund of China (61722506, 61705105, 111574152); National Key R&D Program of China (2017YFF0106403); Final Assembly ‘13th Five-Year Plan’ Advanced Research Project of China (30102070102); Equipment Advanced Research Fund of China (61404150202), The Key Research and Development Program of Jiangsu Province, China (BE2017162); Outstanding Youth Foundation of Jiangsu Province of China (BK20170034); National Defense Science and Technology Foundation of China (0106173); ‘Six Talent Peaks’ project of Jiangsu Province, China (2015-DZXX-009); ‘333 Engineering’ research project of Jiangsu Province, China (BRA2016407, BRA2015294); Fundamental Research Funds for the Central Universities (30917011204, 30916011322); Open Research Fund of Jiangsu Key Laboratory of Spectral Imaging & Intelligent Sense (3091601410414); China Postdoctoral Science Foundation (2017M621747), and Jiangsu Planned Projects for Postdoctoral Research Funds (1701038A).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Qian, J., Tao, T., Feng, S., Chen, Q., Zuo, C. (2019). Robust Dynamic 3D Shape Measurement with Hybrid Fourier-Transform Phase-Shifting Profilometry. In: Zhao, Y., Barnes, N., Chen, B., Westermann, R., Kong, X., Lin, C. (eds) Image and Graphics. ICIG 2019. Lecture Notes in Computer Science(), vol 11903. Springer, Cham. https://doi.org/10.1007/978-3-030-34113-8_11
Download citation
DOI: https://doi.org/10.1007/978-3-030-34113-8_11
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34112-1
Online ISBN: 978-3-030-34113-8
eBook Packages: Computer ScienceComputer Science (R0)