Multi-view Similarity Learning of Manifold Data

Abstract

In recent years, multi-view learning methods have developed rapidly where graph-based approaches have achieved good performance. Usually, these learning methods construct information graph for each view or fuse different views into one graph. In this paper, a novel multi-view learning model that learns one similarity matrix for all views named Multi-view Similarity Learning (MSL) is proposed, where adaptive weights are learned for each view. The multi-view similarity learning method is further extended to kernel space. Experiments of classification, clustering and semi-supervised classification on different real-world datasets show the effectiveness of the proposed method.

This work was supported in part by NSFC Key Projects of International (Regional) Cooperation and Exchanges under Grant 61860206004 and in part by Shenzhen Science & Research Project under Grant JCYJ20170817155854115.

1 Introduction

Usually, in the field of machine learning and pattern recognition, the dimension of data is very high, so how to map high-dimensional data to low-dimensional data and preserve the topology of data is an important issue we are studying now. Then, some classical linear dimensionality reduction methods are proposed, such as Principle Component Analysis (PCA) [5], Linear Discriminant Analysis (LDA) [13], Multidimensional Scaling (MDS) [4]. But the linear dimension reduction method can not represent the manifold structure of data well, so in recent years, many nonlinear dimensionality reduction methods are proposed, such as isometric feature mapping (ISOMAP) [14], local linear embedding (LLE) [8], and Laplacian Eigenmaps (LE) [1]. Laplacian Eigenmaps is a nonlinear dimensionality reduction method for manifold data learning, it can well preserve the nonlinear structure of data space.

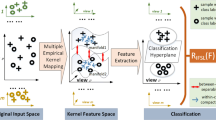
However, in many real world applications, the representation of actual data is not a single form, but can have many forms of expression, such as person’s different angles of faces, which can collect different information from different angles. Usually, for each thing, we observe things from different angles that cannot be observed from another angle, so in order to understand more comprehensive information, we need to observe the problem from multiple angles. Nowadays, we can get different feature from one dataset, we think that compared with single feature, multi-view features can get better results. So for classification, clustering and semi-supervised, we think compared with the single-view similarity learning algorithm, multi-view similarity learning can have the higher accuracy.

Today, in many areas of science, such as pattern recognition, computer vision, genetics, and data mining, we can more easily get data that contain heterogeneous features from samples from different perspectives. In visual data, images can be represented by different descriptors. For example, gray features, gabor features [10], local binary patterns (LBP) features [12], and so on. In image processing, the gabor function is a linear filter for edge extraction. Local binary patterns (LBP) were first proposed as an effective texture description operator, and have been widely used due to their excellent rendering ability for image local texture features. LBP features have significant advantages such as gray invariance and rotation invariance. Because LBP features are simple to calculate and have good effects, LBP features have been widely used in many fields of computer vision.

One of the methods to solve the multi-view problem is to connect vectors from different perspectives into a vector and then on the cascaded vector, directly apply the single view clustering algorithm. However, this connection results in overfitting on small samples and has no meaning to the multi-view problem. Our solution to multi-view is to learn a similarity matrix by adding weights to each view. The weights can be updated through each iteration. Our method can be used for classification, clustering and semi-supervised classification.

The k-nearest neighbor (k-NN) [7] classification algorithm is one of the simplest machine learning algorithms. And k is a very important parameter in the k-NN algorithm. The selection of the k value will affect the classification result of the sample to be classified. However, it is hard to choose a proper neighbor number k beforehand, because if the value of k is too small, the model is easily interfered by noisy data, and if k is too large, the prediction ability of the model is greatly weakened. Generally we use cross-validation to select an appropriate k value.

2 Learning Multi-view Similarity in Laplacian Eigenmaps

In this section, we first introduce a nonlinear dimensionality reduction method LE. And then simply illustrate our multi-view similarity learning algorithms.

2.1 Laplacian Eigenmaps

For the success of the graph-based approach, preserving local manifold structures is an important factor. Laplacian Eigenmaps (LE) is a graph-based dimensionality reduction algorithm and it constructs the relationship between data uses a local angle.

Given a set of data points {$X_1, X_2, \cdots , X_n$}, denote data matrix $X \in \mathcal {R}^{n \times p}$, where n is the number of data points and p is the dimension of features, LE pursues their low dimensional representation $Y_1, Y_2, \cdots , Y_n \in \mathcal {R}^q (q<p)$, which constructs a weighted graph with n points as nodes, and a set of weighted edges connecting neighboring points. If the two data instances i and j are very similar, then i and j should be as close as possible after dimensionality reduction.

The steps are as follows:

• 1. Constructing the Adjacency Graph: Construct neighborhood graph $\mathcal {G}$ through k-nearest neighbors algorithm, k is a preset value. Given n data points $\{X_1, X_2,\cdots , X_n\}$. Nodes i and j are connected if $X_i$ is among k nearest neighbors of $X_j$ or $X_j$ is among k nearest neighbors of $X_i$.

• 2. Choosing the weights: Choose edge weights using heat kernel or simply set edge weight to be 1 if connected and 0 otherwise, or we can get similarity matrix S with heat kernel by:

  $$\begin{aligned} S_{ij}=\exp \left\{ {-\frac{d_{ij}^2}{2r}}\right\} \end{aligned}$$

  (1)

  where $d_{ij}=\Vert X_i-X_j\Vert$, $r>0$ is a suitable constant.

• 3. Eigenmaps: Calculate the eigenvectors and eigenvalues of the Laplacian matrix L by:

  $$\begin{aligned} Lv = \lambda Dv \end{aligned}$$

  (2)

  where D is diagonal matrix and its entries are row sums of S, $D_{ii}=\sum _j S_{ij}$, Laplacian matrix $L=D-S$. We omitting the eigenvector $v_0$ and use the next q eigenvectors for embedding in q-dimensional Euclidean space: $X_i\mapsto Y_i=(v_1(i),v_2(i),\cdots ,v_q(i))^\top$.

2.2 Learning New Multi-view Similarity

For multi-view data, the representation $X^1, X^2,\cdots , X^m$ is the data matrix for each view. $X^v \in R^{n \times p^v}(v=1,2,\cdots ,m)$, where n is the number of data and $p^v$ is the feature dimension of the v-th view. For graph-based methods, each view can build a similar graph and maximize performance by itself. The similarity between two data points in 1 does not reflect the local popular structure of manifold data, so we add a locally linear reconstruction to sample point by its neighbor points. Then for each view, we propose an effective method is to combine these views with the appropriate weights $w_v(v = 1,2,\cdots ,m)$, so our objective function can be written as

$$\begin{aligned}&\min \limits _{S,w}\sum _{v=1}^m w_v^2\Vert X^v - X^vS\Vert ^2_F\\&s.t. \ S_{ij}=S_{ji}\ge 0, S_{ii}=0 \nonumber \end{aligned}$$

(3)

If the distance between sample points are larger, the corresponding reconstruction weight is smaller, and vice versa. We limited reconstruction weight $S_{ij}$ is non-negative, and reconstruction weight is symmetry. Therefore, between sample points we add linear reconstruction constraints to learn the new similarity, so the objective function can be written as

$$\begin{aligned}&\min \limits _{S,w} \sum _{v=1}^m w_v^2\Vert X^v - X^vS\Vert ^2_{F} + \alpha _v \Vert S - S_0^v\Vert ^2_F\\&s.t. \ S_{ij}=S_{ji}\ge 0, S_{ii}=0 \nonumber \end{aligned}$$

(4)

The $L_1$ paradigm can produce relatively sparse solutions, and has the ability to select features. It is useful when solving high-dimensional feature space. Then the minimization of the final objective function of our learning new similarity turns into

$$\begin{aligned}&\min \limits _{S,w} \sum _{v=1}^m ( w_v^2\Vert X^v - X^vS\Vert ^2_F + \alpha _v \Vert S - S_0^v\Vert ^2_F) +\beta \Vert S\Vert _1\\&s.t. \ S_{ij}=S_{ji}\ge 0,\ S_{ii}=0 \nonumber \end{aligned}$$

(5)

2.3 Learning Weight for Each View

Where each view shares the same similarity matrix, so we can get a more accurate similarity matrix by adding appropriate weights to each view. We want the distance between the data points in the same class to be as small as possible, so the objective function of weight can be written as

$$\begin{aligned}&\min \sum _{v=1}^mw_v^2d_v\\&s.t.\ \Sigma _{v=1}^mw_v =1 . \nonumber \end{aligned}$$

(6)

The Lagrange function of Eq. (6) can be written as

$$\begin{aligned}&\min \sum _{v=1}^mw_v^2d_v-\lambda \left( \sum _{v=1}^mw_v-1\right) . \end{aligned}$$

(7)

Taking the derivative of Eq. (7) and setting the derivative to zero, we get the iterative formula for $w_v$ is

$$\begin{aligned}&w_v=\frac{(d_v)^{-1}}{\sum _{v=1}^m(d_v)^{-1}} \end{aligned}$$

(8)

where $d_{ij}=\Vert X_i-X_j\Vert$.

3 Algorithms and Analyses

In this section, we respectively analyze the multi-view similarity learning algorithm for mix-signed data and non-negative data.

3.1 Algorithm for Mix-Signed Data

When the elements of the cell array X are mixed with symbols (some are positive and some are negative), we learn the similarity matrix S by the Eq. (9) iterative update formula. Algorithm 1 summarizes the overall similarity learning iterative update algorithm for mix-signed data. In this algorithm, we set $Q=\sum _{v=1}^m(w_v^2X^{v\top }X^v)$. And in addition to the input cell array X, there are two tuning parameters $\alpha$ and $\beta$. In practice, we found that our algorithm is robust to both parameters $\alpha$ and $\beta$, so in all experiments in this paper, we only set $\alpha =\beta =1$.

Theorem 1

The objective function in Eq. (5) monotonically decreases (ie, does not increase) under the update rule Eq. (9) of Algorithm 1.

$$\begin{aligned} S^{(t+1)}_{ij} \ =\ S^{(t)}_{ij}\ \sqrt{\frac{ [S^{(t)}Q^-\ +\ Q^-S^{(t)}]_{ij}\ +\ 2[Q^++\alpha _vS^v)]_{ij} }{ [S^{(t)}Q^+ +Q^+ S^{(t)} +2\sum _{v=1}^m \alpha _vS^{(t)} ]_{ij}+2Q^-_{ij}\ +\beta )}} \end{aligned}$$

(9)

For proof of Theorem 1, refer to article [2].

3.2 Algorithm for Nonnegative Data

For nonnegative data, we propose a more efficient multi-view similarity learning algorithm to learn the similarity matrix S as in Eq. (10), and we also set $Q=\sum _{v=1}^m(w_v^2X^{v\top }X^v)$. We summarize the multi-view similarity algorithm for nonnegative data in Algorithm 2. And we only set $\alpha = \beta = 1$ in all the experiments of this paper.

Theorem 2

For nonnegative data, the objective function in Eq. (5) decreases monotonically (i.e. it is non-increasing) under the update rule Eq. (10) in Algorithm 2.

$$\begin{aligned} S^{(t+1)}_{ij} \ =\ S^{(t)}_{ij}\ \sqrt{\frac{\ 2[Q+\alpha _vS^v)]_{ij} }{ [S^{(t)}Q \ +\ Q S^{(t)} \ +\ 2\sum _{v=1}^m \alpha _vS^{(t)} ]_{ij}\ +\ \beta ) }} \end{aligned}$$

(10)

For proof of Theorem 2, refer to article [2].

4 Learning Multi-view Similarity in Kernel Spaces

The role of the kernel function is to imply a mapping from low-dimensional space to high-dimensional space $\mathcal {F}$, then in $\mathcal {F}$ space, we learn new similarity for data.

For each view, we use a nonlinear map$: \phi :\ \mathcal {R}^{p^v}\rightarrow \mathcal {F}^v$, $X_i^v\rightarrow \phi (X_i)^v$, the mapped data matrix is $\phi (X)^v=[\phi (X_1)^v,\phi (X_2)^v,\cdots ,\phi (X_n)^v]$. So the minimization objective function becomes

$$\begin{aligned} \min \limits _{S,w} \sum _{v=1}^m ( w_v^2\Vert {\phi (X)}^v - {\phi (X)}^v{S}\Vert ^{2}_{F}+ \alpha _v \Vert S - S_0^v\Vert ^{2}_{F}) +\beta \Vert S\Vert _{1} \end{aligned}$$

(11)

In this paper, four kernel functions are mainly used, include linear kernel, gaussian kernel, cosine kernel and polynomial kernel. In implementation, the mapping $\phi$ does not need to be computed explicitly. By choosing a proper kernel function k, The $\phi$ mapping and $\mathcal {F}$ space can determined implicitly by the dot product between two mapped data samples $\phi (X_i)^v$ and $\phi (X_j)^v$ in $\mathcal {F}$ space by

$$\begin{aligned} k(X^v_i,X^v_j)=(\phi (X_i)^v\cdot \phi (X_j)^v) \end{aligned}$$

(12)

Note that most of kernel functions are nonnegative, such as gaussian kernel and cosine kernel. So we replacing $\phi (X)^{v\top }\phi (X)^v$ with kernel matrix $K^v$ in the iterative updating (10) for non-negative data, then we can get

$$\begin{aligned} S^{(t+1)}_{ij} \ =\ S^{(t)}_{ij}\ \frac{2[\sum _{v=1}^m((w_v^2K^v)+\alpha _vS_0^v)]_{ij}}{[S^{(t)}\sum _{v=1}^m(w_v^2K^v) \ +\ \sum _{v=1}^m(w_v^2K^v) S_0^v \ +\ 2\sum _{v=1}^m \alpha _vS_0^v ]_{ij}\ +\ \beta ) } \end{aligned}$$

(13)

We replacing (10) in Algorithm 2 for nonnegative data with (13), we can obtain the multi-view similarity learning algorithm in kernel space.

5 Experiments

In this section, we first introduce the data set we used. And then we will perform the proposed method on many benchmark datasets and compare it with other related graph-based multi-view learning methods. In the following experiments, we will learn new multi-view similarity matrix with Algorithm 2.

Fig. 1.

Images of toy tiger mapped into the embedding space described by the two coordinates of MSL. Different angles of tiger are shown next to circled points in different parts of the space.

Fig. 2.

Classification accuracy of MSL at four datasets.

Fig. 3.

Classification accuracy of MSL with different kernel functions at ORL dataset.

Fig. 4.

Classification accuracy of MSL with different kernel functions at COIL-100 dataset.

5.1 Brief Description of Data Sets

ORL¹ data set include 400 images with 40 classes. We extract three visual features from each image: gray feature with dimension 4, 096, gabor feature with dimension 2, 560, and LBP feature with dimension 3, 776.

AR² data set include 3, 120 images with 120 class. We extract three visual features from each image: gray feature with dimension 2, 000, gabor feature with dimension 3, 200, and LBP feature with dimension 4, 720.

PIE³ data set is a face data set, we select its subset pose27 that include 1, 440 images with 20 class. We extract three visual features from each image: gray feature with dimension 1, 024, gabor feature with dimension 640, and LBP feature with dimension 944.

Yale⁴ data set include 166 images with 15 class. We extract three visual features from each image: gray feature with dimension 4, 096, gabor feature with dimension 2, 560, and LBP feature with dimension 3, 776.

COIL20⁵ data include 1, 440 images with 20 class. We extract three visual features from each image: gray feature with dimension 1, 024, gabor feature with dimension 640, and local binary pattern (LBP) with dimension 944.

Handwritten numerals⁶ (HW) data set is comprised of 2, 000 data points for 0 to 9 digit classes, 200 data points for each class. We extract three visual features from each image: gray feature with dimension 256, gabor feature with dimension 160, and LBP feature with dimension 236.

The COIL100⁷ data set contains 7, 200 colorized images corresponding to 100 different objects in 72 different viewpoints. We extracted 7 features from each image, including the gray scale features features and other six channels in the RGB and HSV channels, all of which are characterized by 16, 384 dimensions.

Caltech101⁸ data set is containing 101 categories of images. We select 1, 474 images with 7 classes, include Dolla-Bill, Face, Garfield, Motorbikes, Snoopy, Stop-Sign and Windsor-Chair. Six features are extracted from all the images, include 48 dimension gabor feature, 40 dimension wavelet moments, 254 dimension CENTRIST feature, 1, 984 dimension HOG feature, 512 dimension GIST feature, and 928 dimension LBP feature.

5.2 Low Dimensional Embedding

In this part, we use one class of COIL-100 datasets, this class containing 72 images at different angles, we embedding high-dimensional images data into low-dimensional space. We can see in Fig. 1, these 72 images are rotated at different angles, so when embedding to a two-dimensional space, the closer to a circle. We extracted the gray feature and RGB features of each channel, and found that the performance after fusion is better than that of a single channel features. Figure 1 showing the results of a single channel and channel fusion, and there is a corresponding picture next to each point.

Figure 1 shows the 2-D embedding results of single-view and multi-view with each row corresponding to one manifold benchmark. From the figure, we can see our method MSL is more robust and can effectively find the proper low-dimensional embedding.

5.3 Classification of MSL

In this section, in order to validate the performance of the proposed method, we apply our method into multi-view classification. We used the indicator accuracy (ACC) [6] to evaluate the performance of the algorithm on four benchmark datasets. The four datasets we used are ORL, Yale, AR, and PIE. Each database is randomly divided into a training set and a test set, with different numbers of images being used for training.

The neighbor number k in computing heat kernel similarity of MSL are tuned such that MSL reach its best classification performance. We set the parameters $\alpha = \beta = 1$. The classification accuracy is computed by the nearest neighbor classifier.

To test the performance of the multi-view similarity learning in kernel spaces computed in (13), we test the classification accuracy of single-view and multi-view new similarity learning method with different kernel functions on ORL database. In this paper, four kernel functions (linear, polynomial, cosine, and Gaussian) are adopted in the experiments. We test MSL with tenfold cross-validation [3] as different number of embedded dimension is chosen. Figure 2 shows the classification accuracy of the single-view feature on the four data sets and the classification accuracy after the fusion of the three features. Figure 3 shows the classification performance variations of MSL with different kernel functions, and the classification performance variations of single-view and multi-view. And from the Fig. 3, We can see that classification performance of multi-view is better than classification performance of single-view on any kernel. From the Fig. 4, we extracted the fours features include gray feature and features of the RGB three channels of the picture and then calculate the classification accuracy of each channel, and classification accuracy of fusion with multiple channels, we can see the classification accuracy after fusion is higher than the classification accuracy of a single channel.

Table 1. Clustering accuracy of MSL on two datasets

5.4 Clustering of MSL

In this section, we compared our method with other two multi-view learning methods, one is Multi-view Spectral Clustering (MVSC) [9] and the other is Multi-view Learning with Adaptive Neighbours (MLAN) [11], Table 1 show the clustering result in terms of accuracy of different method in two different datasets, SC is single-view feature. We can see our clustering results are better than the other two methods.

Table 2. Semi-supervised classification accuracy of MSL on three datasets

5.5 Semi-supervised Classification of MSL

In this section, we compared our method with MLAN [11] method, and in terms of semi-supervised classification, we choose the front $20\%$ data as labeled sample, Table 2 show the semi-supervised classification performance of different method in three different datasets, we can see that our method is better than other method.

6 Conclusion and Remarks

In this paper, we introduce a novel multi-view similarity learning method named MSL, and our method can preserves the manifold structure of the data. For multi-view learning, our method can automatically learns weights for each view. The experimental results on real world benchmark data sets demonstrate that the classification accuracy of multi-view features is higher than that of single-view feature. And in clustering and semi-supervised classification, the accuracy of our method is higher than that of other multi-view methods. These experimental results demonstrate the effectiveness of our method.