Abstract
The validity of learning-based image super-resolution is largely limited by supporting dataset. Neither external-based nor internal-based super-resolution methods can perform well in real applications such as medical endoscopic images. This paper studies the strategy of joint learning of two kinds of methods. We first build sub-dictionaries and study the corresponding mapping matrices on the respective samples. Due to the consistency of learning strategies, we establish joint mapping matrices based on the distance between the input low-resolution image patches and the dictionary atoms in the reconstruction phase. We adopt the nearest neighbor strategy and the weighted joint strategy to obtain the new mapping matrix. The high-resolution image is reconstructed by the new mapping model. The experiments prove the effectiveness of our strategy.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Single image super-resolution (SISR) aims to recover a high-resolution (HR) image from the input low-resolution (LR) image via complex linear or nonlinear models. The SR problem arises in many practical applications, such as medical imaging and video applications [13, 21]. It is a classical problem in low-level computer vision and has attracted a lot of research attention. In recent years, numerous approaches have been proposed to solve this problem. In general, SR algorithms can be divided into three categories: interpolation-based methods [8, 12], reconstruction-based methods [4, 14], and learning-based methods [16, 17, 21].
Interpolation-based methods [8, 12], such as the bilinear method and bicubic method, are efficient, but tend to generate oversmoothing images. Another class of SR approach is based on reconstruction [4, 14]. These methods estimate an HR image by enforcing some reasonable assumptions or prior knowledge to it. However, the high frequency details in images are not reconstructed very well [1].
The most popular method for SR now is the third category, which is known as learning-based method. These approaches usually assume that the lost high-frequency details in LR images can be predicted by the learned information from training set, which consists of a large set of LR patches and HR patches. These methods attempt to capture the co-occurrence prior between LR and HR image patches. Inspired by compressed sensing, Yang et al. [21] adopted sparse representation to solve SR problem. Timofte et al. [16] proposed an anchored neighborhood regression (ANR) method, which learned a sparse dictionary and utilized the sparse dictionary atoms for ridge regression, while, its refined variant, A+ [17], utilized the neighborhood taken from the training pool of samples for each sparse dictionary atom. Deep learning has also been adopted to address SR problem. Dong et al. [5] proposed a super-resolution convolutional neural network (SRCNN) for SR. Kim et al. [11] presented a very deep networks for super-resolution.
According to the ways of extracting training examples, learning-based SR method can be split into two classes. One uses an external database of natural images [3, 5, 11, 16, 17, 20,21,22] and the other utilizes a database obtained from the input LR image itself [2, 6, 7].
The external example-based methods are based on the assumption that the mapping model between LR and HR image patches can be learned from an external database. The methods above are almost external example-based SR models. The internal example-based methods assume that the patches in a natural image tend to redundantly recur many times inside the image, both within the same scale, as well as across different scales [7]. Bevilacqua et al. [2] generated a double pyramid of recursively scaled and interpolated images, thus built a dictionary from the input LR image itself.
External example-based SR methods and internal example-based SR methods both have their own advantages and disadvantages, for example, some features of medical endoscopic images can not be well represented by widely used training set. Therefore, we can jointly train the model to get better medical image super-resolution results. Wang et al. [18] defined two loss functions using sparse coding-based external exmaples, and epitomic matching based on internal examples. Timofte [15] proposed a method, which fused A+ [17] and CSCN [19] as a new image feature, and applied the anchor strategy for SR. However, both of them adopted two different SR strategies and are based on the results of reconstruct HR image patches. In this paper, We propose novel joint SR to adaptively integrate the merits of both external-based and internal-based SR methods. What’s more, we can fuse the mapping matrices in training phase, and thus obtain fusion matrices.
The remainder of the paper is as follows: Sect. 2 details the universal fusion strategy for SR. Section 3 shows the experimental results. Conclusion follows in Sect. 4.
2 Proposed Method
In the external example-based SR methods, we cannot guarantee that any input image patch can be matched and expressed by a limited set of external database. When dealing with some textures which are missing in the external database, the SR results may be oversmoothing and product serious noise. Internal strategy can handle this situation. But it can not perform well when the image has some patches that rarely recur. So it is reasonable that jointly learning for SR from external and internal examples.
However, there are lots of different SR methods. With different SR methods, it is hard to identify that the result of the final improvement is from whether the two different SR approaches or the combination of two different example selection strategies. For the purpose of getting a universal conclusion, we adopt the same strategy, A+ [17], based on external examples and internal examples respectively, to obtain a joint SR model. In this way, the improvement only depends on a combination of samples.
2.1 Training Model
We adopt the same training strategy with A+ to obtain the mapping matrix for each anchor point.
In external example-based A+ method, we apply K-SVD to get a sparse dictionary \(\mathbf {A}_e\). Each atom of the dictionary is regarded as an anchor point. We search \(N_e\) nearest neighbors in the training set to conduct a sub-dictionary pair \(\{\mathbf {D}_{He}^{ke}, \mathbf {D}_{Le}^{ke}\}_{ke=0}^{N_e}\) for each anchor point.
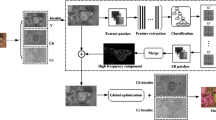
As for internal example-based A+ method, we adopt the double pyramid method to get the internal database. As shown in Fig. 1, we regard the input LR image \(\mathbf {Y}\) as an HR training image. The other HR training images are generated by scaling down the LR input image \(\mathbf {Y}\) with small factor \(p_i\). So the HR training set is denoted as \(\{ \mathbf {Y}_H^i\}_{i=0}^{N_s}\), and \(N_s\) is the number of generated HR images. The LR image training set is conducted by scaling down each HR image with factor s, which is the same with the factor in reconstruction step. We also rotate and flip the input LR image for data augmentation. Then, we can conduct an HR and LR patch set for training. With the training set obtained, a similar sparse dictionary \(\mathbf {A}_i\) is learned by K-SVD. For each anchor point in sparse dictionary, we also conduct the sub-dictionary pair \(\{\mathbf {D}_{Hi}^{ki}, \mathbf {D}_{Li}^{ki}\}_{ki=0}^{N_i}\), \(N_i\) is the number of anchor points in internal model.
2.2 Mapping Model
In this paper, we adopt the ridge regression for learning the mapping matrix. We take the external example-based method as example, the regression is formulated as:
where \(\mathbf {y}_l\) is an input LR patch. \({\mathbf {D}}_{Le}^{ke}\) is the corresponding sub-dictionary of \(\mathbf {y}_l\), and ke is the index and is depended on the distance between anchor point and LR patch \(\mathbf {y}_l\). \(\mathbf {w}\) is the representation of \(\mathbf {y}_l\) on sub-dictionary \(\mathbf {D}_{Le}^{ke}\).
Equation 1 has a closed-form solution:
Thus, we can get the corresponding HR image patch \(\mathbf {y}_h\) using the same coefficient on HR sub-dictionary \(\mathbf {D}_{He}^{ke}\):
We can obtain the mapping matrix \(\mathbf {P}_e^{ke}\):
The mapping matrix \(\{\mathbf {P}_i^{ki}\}_{ki=0}^{N_i}\) in internal example-based method also can be computed in the same way.
2.3 Fusion Model and Image SR Reconstruction
In this stage, the input LR image are divided into overlapped image patches \(\{\mathbf {y}_i\}_{i=0}^{N}\). The underlying HR image patches are noted as \(\{\mathbf {x}_i\}_{i=0}^{N}\). Once we get the mapping matrices \(\{\mathbf {P}_e^{ke}\}_{ke=0}^{N_e}\) and \(\{\mathbf {P}_i^{ki}\}_{ki=0}^{N_i}\), we need to fuse them based on the distance between input LR patch and anchor point in \(\mathbf {A}_e\) and \(\mathbf {A}_i\) respectively.
We denote \(\mathbf {d}_e\) and \(\mathbf {d}_i\) as the minimum distance between LR input patch \(\mathbf {y}_i\) and anchor points in \(\mathbf {A}_e\) and \(\mathbf {A}_i\) respectively. In this paper, cosine distance is chosen as distance metric. So the greater the value, the closer the distance. We attempt two joint strategies.
The first one we call nearest strategy. For each input LR patch \(\mathbf {y}_i\), we compare \(\mathbf {d}_e\) with \(\mathbf {d}_i\). If \(\mathbf {d}_e\) is bigger than \(\mathbf {d}_i\), it means the anchor point generated by external example-based method is closer than internal one. Thus, we choose the external mapping matrix \(\mathbf {P}_e^{ke}\).
The other is weighted strategy. According to the distance \(\mathbf {d}_e\) and \(\mathbf {d}_i\), we give different weights to two mapping matrices \(\mathbf {P}_e^{ke}\) and \(\mathbf {P}_i^{ki}\).

where, \(w_1\) and \(w_2\) are weights that balance the two mapping matrices. Since the bigger the value of \(\mathbf {d}_e\) and \(\mathbf {d}_i\), the closer the distance, the corresponding weight should also be bigger than another. Thus, if \(\mathbf {d}_e\) is bigger than \(\mathbf {d}_i\), \(w_1\) should also be bigger than \(w_2\). We apply a simple weighted strategy to our model:

Once the fusion mapping matrix is got, we directly use it to reconstruct the underlying HR image patch \(\mathbf {x}_i\).
The desired HR image \(\mathbf {X}\) is reconstructed by merging all the HR image patches \(\{{\mathbf {x}_i}\}_{i=0}^N\), and averaging the overlapping regions between the adjacent patches.
3 Experimental Results
In this section, we first compare the proposed method with external A+ method and internal A+ method to evaluate the validity of fusion strategy. We also compare it with several representative SISR methods, including external-based methods ScSR [21], Zeyde’s [22], A+[17], internal-based method SelfEx [9] and deep method SRCNN [5]. All the experiments are carried out in the Matlab (R2016a) environment. For fair comparison, the external example-based methods are all trained on 91-image dataset [21]. The peak signal-to-noise ratio (PSNR) and structural similarity (SSIM) are applied to evaluate the quality of SR reconstruction and results are listed in Tables 1 and 3. We use three testing set (Set5, Set14 and B100) for SR evaluation.
3.1 Implementation Details
We convert RGB color space into YCbCr color space and apply the proposed algorithm on luminance channel (Y) and up-sample color channels (CbCr) by interpolation since human vision is much more sensitive to illuminance changes. The magnification factor is 3. The size of LR and HR image patch is \(5 \times 5\) with overlapping 4 pixels. The features of LR images are the first and second order derivatives of the patches. The features of HR images are the residual between ground truth and the interpolated LR images, and represent the lost high frequency details. The number of generated HR images, \(N_s\) is 19, which means there are 20 HR images (including the input image itself). We also make a data argumentation for training. We rotate the image in 64 angles, and there is a 5.625\(^\circ \) difference in each angle. The size of sparse dictionary in external part is 2048, i.e. \(N_e\) is 2048. \(N_i\), the size in internal part, is 1024. The regularization parameter, \(\lambda \), is set as 0.01.
3.2 Quality Evaluation
Table 1 shows average performance of fusion using two different strategies. Compared with external A+ SR method and internal A+ SR method, both joint methods can improve the SISR result, indicating the effectiveness of the method. And nearest strategy defeats weighted strategy, which impels us to use it in the rest of the experiment.
Table 2 shows the PSNR results on Set5. Our method achieves the best performance on most test images. We also compare the proposed method (with nearest strategy) with some state-of-the-art SR methods on Set14 and BSD100. Table 3 shows the average PSNR and SSIM results for up-scaling factor 3. Our method outperforms external, internal, and deep-based methods on all datasets. The average SSIM also performs best, revealing that our reconstructed results achieve best structural similarity with the ground truth. We also collect some medical endoscopic images for visual comparison, as shown in Fig. 2. We can see that our method (with nearest strategy) recovers more visually pleasing results with fewer artifacts, more accurate details and sharper edges.
4 Conclusion
External-based and internal-based super-resolution methods both have their own advantages. This paper studies the strategy of joint learning of two kinds of methods and propose a universal fusion strategy for super-resolution. We utilize the strategy, which is the same with A+ [17], to obtain a external sub-dictionaries and internal sub-dictionaries. Then, we use the nearest strategy and weighted strategy to fuse the external and internal mapping matrices. The high-resolution image is reconstructed by the new mapping model. The experiments prove the effectiveness of our strategy.
References
Baker, S., Kanade, T.: Limits on super-resolution and how to break them. IEEE Trans. Pattern Anal. Mach. Intell. 24(9), 1167–1183 (2002)
Bevilacqua, M., Roumy, A., Guillemot, C., Morel, M.L.A.: Single-image super-resolution via linear mapping of interpolated self-examples. IEEE Trans. Image Process. 23(12), 5334–5347 (2014)
Chang, H., Yeung, D.Y., Xiong, Y.: Super-resolution through neighbor embedding. In: 2004 Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, CVPR 2004, vol. 1, p. I. IEEE (2004)
Dai, S., Han, M., Xu, W., Wu, Y., Gong, Y.: Soft edge smoothness prior for alpha channel super resolution. In: 2007 IEEE Conference on Computer Vision and Pattern Recognition, pp. 1–8. IEEE (2007)
Dong, C., Loy, C.C., He, K., Tang, X.: Image super-resolution using deep convolutional networks. IEEE Trans. Pattern Anal. Mach. Intell. 38(2), 295–307 (2016)
Freedman, G., Fattal, R.: Image and video upscaling from local self-examples. ACM Trans. Graph. (TOG) 30(2), 12 (2011)
Glasner, D., Bagon, S., Irani, M.: Super-resolution from a single image. In: 2009 IEEE 12th International Conference on Computer Vision, pp. 349–356. IEEE (2009)
Hou, H., Andrews, H.: Cubic splines for image interpolation and digital filtering. IEEE Trans. Acoust. Speech Signal Process. 26(6), 508–517 (1978)
Huang, J.B., Singh, A., Ahuja, N.: Single image super-resolution from transformed self-exemplars. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 5197–5206 (2015)
Jiang, J., Ma, X., Chen, C., Lu, T., Wang, Z., Ma, J.: Single image super-resolution via locally regularized anchored neighborhood regression and nonlocal means. IEEE Trans. Multimed. 19(1), 15–26 (2017)
Kim, J., Kwon Lee, J., Mu Lee, K.: Accurate image super-resolution using very deep convolutional networks. In: Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pp. 1646–1654 (2016)
Li, X., Orchard, M.T.: New edge-directed interpolation. IEEE Trans. Image Process. 10(10), 1521–1527 (2001)
Park, S.C., Park, M.K., Kang, M.G.: Super-resolution image reconstruction: a technical overview. IEEE Signal Process. Mag. 20(3), 21–36 (2003)
Sun, J., Xu, Z., Shum, H.Y.: Image super-resolution using gradient profile prior. In: 2008 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2008, pp. 1–8. IEEE (2008)
Timofte, R.: Anchored fusion for image restoration. In: 2016 23rd International Conference on Pattern Recognition (ICPR), pp. 1412–1417. IEEE (2016)
Timofte, R., De Smet, V., Van Gool, L.: Anchored neighborhood regression for fast example-based super-resolution. In: Proceedings of the IEEE International Conference on Computer Vision, pp. 1920–1927 (2013)
Timofte, R., De Smet, V., Van Gool, L.: A+: adjusted anchored neighborhood regression for fast super-resolution. In: Cremers, D., Reid, I., Saito, H., Yang, M.-H. (eds.) ACCV 2014. LNCS, vol. 9006, pp. 111–126. Springer, Cham (2015). https://doi.org/10.1007/978-3-319-16817-3_8
Wang, Z., Yang, Y., Wang, Z., Chang, S., Yang, J., Huang, T.S.: Learning super-resolution jointly from external and internal examples. IEEE Trans. Image Process. 24(11), 4359–4371 (2015)
Wang, Z., Liu, D., Yang, J., Han, W., Huang, T.: Deep networks for image super-resolution with sparse prior. In: Proceedings of the IEEE International Conference on Computer Vision, pp. 370–378 (2015)
Yang, J., Wang, Z., Lin, Z., Cohen, S., Huang, T.: Coupled dictionary training for image super-resolution. IEEE Trans. Image Process. 21(8), 3467–3478 (2012)
Yang, J., Wright, J., Huang, T.S., Ma, Y.: Image super-resolution via sparse representation. IEEE Trans. Image Process. 19(11), 2861–2873 (2010)
Zeyde, R., Elad, M., Protter, M.: On single image scale-up using sparse-representations. In: Boissonnat, J.-D., et al. (eds.) Curves and Surfaces 2010. LNCS, vol. 6920, pp. 711–730. Springer, Heidelberg (2012). https://doi.org/10.1007/978-3-642-27413-8_47
Acknowledgment
This work was supported by the Natural Science Foundation of China (Nos. 61471216 and 61771276), the National Key Research and Development Program of China (No. 2016YFB0101001) and the Special Foundation for the Development of Strategic Emerging Industries of Shenzhen (Nos. JCYJ20170307153940960 and JCYJ20170817161845824).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2019 Springer Nature Switzerland AG
About this paper
Cite this paper
Wang, W., Shang, X., Yang, W., Zhang, C., Liao, Q. (2019). A Universal Fusion Strategy for Image Super-Resolution Jointly from External and Internal Examples. In: Zhao, Y., Barnes, N., Chen, B., Westermann, R., Kong, X., Lin, C. (eds) Image and Graphics. ICIG 2019. Lecture Notes in Computer Science(), vol 11901. Springer, Cham. https://doi.org/10.1007/978-3-030-34120-6_58
Download citation
DOI: https://doi.org/10.1007/978-3-030-34120-6_58
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-030-34119-0
Online ISBN: 978-3-030-34120-6
eBook Packages: Computer ScienceComputer Science (R0)