Keywords

1 Introduction

Neural Networks have been widely used to solve different real world problems in different arenas because of its remarkable function approximation capability. Recently, Deep Neural Networks have attained much awaited attention across various discipline. Despite of all the advances in the field of Deep Learning, including the arrival of better and improved optimization algorithms and GPUs, several questions are still puzzling. One of them is the optimum architecture size. This includes, how one should decide the number of nodes and number of layers for a network to solve a particular problem using the data set. Both the deep and shallow networks have their own share of advantages and disadvantages. This makes it difficult for the network designer to create the optimum architecture. Shallow networks exhibit better generalization performance and learn faster, but have a higher tendency to overfit [5]. Deeper networks like LeNet-300-100 or LeNet-5 [12], form complex decision boundaries but avoids overfitting.

Model Compression techniques are inspired by the fault tolerance property to network damage conditions, seen in larger networks. Pruning is one such model compression technique. Introducing damage to the network purposefully will compromise its performance in terms of accuracy. However, a procedure of retraining can be used to regain the original performance. In general, the percentage reduction in accuracy is proportional to the amount of damage made. When the damage to the network is rigorous, the network requires more retraining to regain the desired accuracy on the particular data set. [18] conducted experiments comparing the accuracy of large, but pruned models (large-sparse) with their smaller, but dense (small-dense) counterparts and gave results stating that the large-sparse models outperforms the small-dense models with 10\(\times \) reduction in the number of non zero parameters with minimal reduction in accuracy.

Major Contributions. The contributions of this paper are summarized as follows: (1) We derive theoretical bounds for the number of epochs a pruned network will require to reach the original performance, relative to the number of epochs the original unpruned network had taken to reach the same performance. (2) We derive a relation bounding the error that will be present at the output based on layer-wise error propagation due to the pruning done in different layers. (3) A new parameter ‘Net Deviation’ is proposed, that could serve as a measure to select the appropriate pruning method for a particular network and data, by comparing the net deviation curves for these methods for different percentage of pruning. This parameter could be an alternative to ‘test accuracy’ that is normally used. Net Deviation is calculated while pruning, using the same data that was used for pruning. The detailed proofs of the stated theorems are given in the Appendix.

2 Related Works

Research in the area of architecture selection has led to different pruning approaches. Recently, obtaining a desired network architecture received significant attention from various researchers [10, 14, 17] and [11]. Network pruning was found to be a viable and popular alternative to optimize an architecture. This research can be dichotomised into two categories, with and without retraining.

2.1 Without Retraining

The weights which contribute maximum to the output must not be disturbed, if no retraining is required. In order to achieve this, [7] have used the idea of Core-sets that could be found through SVD or Structured Sparse PCA or an activation-based procedure. Even when this method could provide a high compression, the matrix decomposition complexity involved could be higher for larger networks.

2.2 With Retraining

Most of the research works focus on methods that have a retraining or fine-tuning step after pruning. Such methods can be classified again as given below:

As an Optimization Procedure. In this category, retraining is defined as a procedure over the trained model to find the best sparse approximation of the trained model, that doesn’t reduce the overall accuracy of the network. [4] does the same in two steps- one to learn the weights that can approximate a sparser matrix (L step) and another to compress the sparser matrix again (C step). [1] does model compression by considering model compression as a convex optimization algorithm. Minor fine tuning is also done at the end of this retraining procedure.

Without Any Optimization Procedure. A pruning scheme without any optimization procedure, delves into two things: either to keep the prominent nodes or to remove redundant nodes using some relevant criteria. Prominent nodes are defined as the nodes that contribute the most to the output layer nodes. These nodes could be defined based on the weight connections or gradients, as seen in [3, 8, 9, 13] and [6]. Redundant nodes can be removed by clustering nodes that give similar output as done in [14]. Data-free methods also exist, like [15] that does not use the data to calculate the pruning measure.

3 Analysis of Retraining Step of a Sparse Neural Network

3.1 Preliminaries

Consider a Multi-Layer Perceptron with ‘L’ layers, with \(n^{(l)}\) nodes in layer l. Corresponding weights and biases are denoted as \(\mathbf W ^{(1)}, \mathbf W ^{(2)},..., \mathbf W ^{(L-1)}\) and \(\mathbf B ^{(2)}, \mathbf B ^{(3)},..., \mathbf B ^{(L)}\) respectively, where \(\mathbf W ^{(l)} \in \mathbb {R}^{n^{(l)} \times n^{(l+1)}}\) and \(\mathbf B ^{(l)} \in \mathbb {R}^{n^{(l)} \times 1}\). The loss function is denoted as \(L(\mathbf W )\). This could be mean-squared error or cross-entropy loss, defined on both the weights and biases, using the labels and the predicted outputs.

3.2 Error Propagation in Sparse Neural Network

Pruning process can be made parallel if the same is done layer wise. For the same cause, the layer wise error bound, with respect to the overall allowed error needs to be known. This section hence looks into the individual contributions of the change in the parameter matrices in each layer to the final output error. The output of the neural network is given as

$$\begin{aligned} \mathbf Y ^{(L)} = f(\mathbf W ^{(L-1)^T}{} \mathbf Y ^{(L-1)} + \mathbf B ^{(L)}) \end{aligned}$$
(1)

The deviation introduced in the output error \(\delta \mathbf Y ^{(L)}\), due to pruning the parameter matrices \(\mathbf W ^{(L-1)}\) by \(\delta \mathbf W ^{(L-1)}\), can be bounded as

$$\begin{aligned} ||\delta \mathbf Y ^{(L)}|| \le ||\frac{\partial \mathbf Y ^{(L)}}{\partial \mathbf W ^{(L-1)}} \delta \mathbf W ^{(L-1)}|| + ||\frac{\partial \mathbf Y ^{(L)}}{\partial \mathbf Y ^{(L-1)}} \delta \mathbf Y ^{(L-1)}|| \end{aligned}$$
(2)

Theorem 1

Assuming that the input layer is left untouched, the output error introduced by pruning the trained network \(N(\{\mathbf{W }_l\}_{l=1}^L, \mathbf X )\) will always be upper bounded by the following relation,

$$\begin{aligned} ||\delta \varvec{Y}^{(L)}|| \le \sum _{l=2}^{L} \Bigg [ \underset{(l\ne L)}{\prod _{i = l+1}^{L}} ||\frac{\partial \varvec{Y}^{(i)}}{\partial \varvec{Y}^{(i-1)}}|| \Bigg ] ||\frac{\partial \varvec{Y}^{(l)}}{\partial \varvec{W}^{(l-1)}}|| ||\delta \varvec{W}^{(l-1)}|| \end{aligned}$$
(3)

The above relation essentially explains the accumulation of the error in each layer to produce the error in the final layer i.e., if \(\epsilon \) is the total allowed error in the final layer, then it can be bounded by the sum of individual layer errors, \(\epsilon _l\) (\(l = 2,3,..., L\)) as shown below:

$$\begin{aligned} \epsilon \le \epsilon _2 + \epsilon _3 + ... + \epsilon _L \end{aligned}$$
(4)

The above equation sets apart error bounds on different layers and will be of much help in optimisation-based pruning techniques.

\(\epsilon _L = ||\frac{\partial \mathbf Y _L}{\partial \mathbf W _L} \delta \mathbf W _L ||\)

and \(\epsilon _l = \Bigg [ \underset{}{\prod _{i = l+1}^{L}} ||\frac{\partial \mathbf Y ^{(i)}}{\partial \mathbf Y ^{(i-1)}}|| \Bigg ] ||\frac{\partial \mathbf Y ^{(l)}}{\partial \mathbf W ^{(l-1)}}|| ||\delta \mathbf W ^{(l-1)}||\), for \(l\ne L\)

The assumption of \(\epsilon _l = 0\) results in a simple relation given in Eq. (5), which can help in explaining two design practices used in classification networks:

$$\begin{aligned} \delta \mathbf W ^{(l-1)^T} \mathbf Y ^{(l-1)} = \mathbf 0 \end{aligned}$$
(5)
  1. 1.

    An optimised structure of Multi-Layer Perceptrons used for classification will have \(n^{(l)} \ge n^{(l+1)}\), where \(n^{(l)}\) denotes the number of nodes in layer l and \(l = 2,3,...,L \).

    Since \(\mathbf W ^{(l)} \in \mathbb {R}^{n^{(l)} \times n^{(l+1)}}\) and \(\mathbf Y ^{(l)} \in \mathbb {R}^{n^{(l)} \times 1}\), for Eq. (5) to have a solution, \(n^{(l)} \ge n^{(l+1)}\). Thus the minimum number of nodes the hidden layers can have equally to help the network train well from the data, is the number of nodes in the output layer.

  2. 2.

    Data dependent approaches results in better compression models.

    Each neural network is unique because of its architecture and the data it was trained on. Any pruning approach must not change the behaviour of the network with respect to the application it was destined to perform. Consider \(\mathbf Y ^{(l)} \in \mathbb {R}^{n^{(l)} \times B}\), where B is the batch size and \(\mathbf W ^{(l)} \in \mathbb {R}^{n^{(l)} \times n^{(l+1)}}\). For Eq. (5) to be satisfied, the column space of \(\mathbf Y ^{(l)}\) must lie in the null space of \(\delta \mathbf W ^{(l)}\) and vice-versa. This implies that the entries for the appropriate \(\delta \mathbf W ^{(l)}\) can be obtained when the pruning measure is coined based on the features obtained from that layer.

3.3 Net Deviation(D)

Different pruning algorithms are currently present for model compression. A measure, similar to test accuracy, for comparing different pruning approaches based on the compression ratios, is the normalized difference between the obtained error difference and the bound, which is defined as Net Deviation, given in (6). An example explaining the use of D, is given in Sect. 4.1.

$$\begin{aligned} D = ||\delta \mathbf Y ^{(L)}|| - \sum _{l=2}^{L} \Bigg [ \underset{(l\ne L)}{\prod _{i = l+1}^{L}} ||\frac{\partial \mathbf Y ^{(i)}}{\partial \mathbf Y ^{(i-1)}}|| \Bigg ] ||\frac{\partial \mathbf Y ^{(l)}}{\partial \mathbf W ^{(l-1)}}|| ||\delta \mathbf W ^{(l-1)}|| \end{aligned}$$
(6)

3.4 Theoretical Bounds on the Number of Epochs for Retraining a Sparse Neural Network

Assume that the loss function is continuously differentiable and strictly convex. The losses decide the number of epochs the network takes to reach convergence and hence, the number of epochs to reach convergence can be viewed to be directly proportional to the loss. If the total number of parameters in the network is M, the parameters can be made p-sparse in \(\frac{M!}{p!(M-p)!}\) number of ways. Hence, the bounds provided below must be understood in the average sense. Adding a regularisation term still keeps the loss function strongly convex, if the initial loss function is strongly convex. This makes Theorem 2 and all the accompanying relations valid even for loss functions with regularisation terms.

Theorem 2

Given a trained network \(N(\{\mathbf{W }_l\}_{l=1}^L, \mathbf X )\), trained from initial weights \(\mathbf W _{initial}\) using \(t_{initial}\) epochs. For fine-tuning the sparse network \(N_{sparse}( \{\mathbf{W }_l\}_{l=1}^L,\) \( \mathbf X )\), there exists a positive integer \(\gamma \) that lower bounds the number of epochs \((t_{sparse})\) to attain the original performance as,

$$\begin{aligned} t_{sparse} \ge \frac{\gamma \mu _1}{\mu _2} \Bigg [ \frac{||\nabla L(\mathbf W _{initial}) ||^2}{||\nabla L(\mathbf W _{sparse}) ||^2}\Bigg ] t_{initial} \end{aligned}$$
(7)

When there are different hidden layers, the gradients would follow the chain rule and the following equation can be incorporated in (7) to obtain the bound.

$$\begin{aligned} ||\nabla L(\mathbf W ) ||^2 = ||\nabla L(\mathbf W ^{(1)}) ||^2 + ||\nabla L(\mathbf W ^{(2)}) ||^2 + ... + ||\nabla L(\mathbf W ^{(L-1)}) ||^2 \end{aligned}$$
(8)

The definitions for \(\mu _1\) and \(\mu _2\) vary for connection and node pruning and are given below. The equations are written for pruning the trained model with final parameter matrix \(\mathbf W ^*\). \(\mathbf W ^{'}\) could be either the initial or sparse matrix. Connection Pruning: Taking advantage of the fact that connection pruning results in a sparse parameter matrix of the same size as that of the unpruned network, \(\mu \) can be defined as:

$$\begin{aligned} \mu ^{'} \le \dfrac{||\nabla L(\mathbf W ^{'}) - \nabla L(\mathbf W ^*)||}{||\mathbf W ^{'} - \mathbf W ^*||} \end{aligned}$$
(9)

Node and Filter Pruning: Node and filter pruning reduces the rank of the parameter matrix and hence Eq. (9) cannot be used. PL inequality is used instead.

$$\begin{aligned} \mu ^{'} \le \dfrac{||\nabla L(\mathbf W ^{'})||^2}{||L(\mathbf W ^{'}) - L(\mathbf W *)||} \end{aligned}$$
(10)
Fig. 1.
figure 1

Comparison of the three pruning methods for different percentage of pruning using Net Deviation ((a) and (b)) and Test Accuracy in (c). (a) and (c) are results on LeNet-300-100 and (b) are of LeNet-5

Full size image

4 Experimental Results and Discussion

Simulations validating the theorems stated were performed on two popular networks: LeNet-300-100 and LeNet-5 [12], both trained on MNIST digit data set and had test accuracies of 97.77% and 97.65% respectively.

Table 1. The number of epochs taken for fine-tuning LeNet-300-100 pruned at different pruning and sparsity ratios.
Full size table
Table 2. The number of epochs taken for fine-tuning LeNet-5 pruned at different pruning and sparsity ratios.
Full size table

4.1 Analysis of Net Deviation

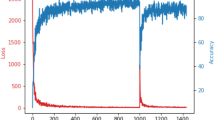
To explain the application of the parameter ‘Net Deviation’, LeNet-300-100 and LeNet-5 were pruned using Random, Weight magnitude based and Clustered Pruning approaches. In random pruning, the connections were made sparse randomly, while in clustered pruning, the features of each layer were clustered to the required pruning level. One out of each node or filter in the cluster is kept. The second method chose the nodes that had higher weight magnitude connections. The results for different percentage of pruning in an average sense, are given in Fig. 1, which explains that, for lower level of pruning, D is lower for random pruning approach. But for higher pruning or higher model compression, random pruning is not a good pruning method to look into. Net deviation is calculated using the same batch of data that was used for pruning. A similar comparison has been done on LeNet-300-100 using test accuracy as the parameter and the results are shown in Fig. 1(c). It could be seen that when choosing the appropriate method for pruning, for a particular data set and network, test accuracy does not give much information with respect to the amount of compression or the percentage of pruning. Because of similar inferences, random pruning could be applied by a user, who wants smaller compression, with lower computational complexity as random pruning is computationally less expensive than clustered pruning.

4.2 Theoretical Bounds on the Number of Epochs for Retraining a Sparse Neural Network

Both the networks were pruned randomly with the same seed in two ways: Connection Pruning and Node Pruning. Tables 1 and 2 show the results obtained at different pruning ratios for LeNet-300-100 and LeNet-5 respectively. For LeNet-300-100 pruned at pruning ratios 0.1, 0.5 and 0.9 and for sparsity ratios of 0.1, 0.6 and 0.9, the value of \(\gamma \) was obtained as 0.01, 1 and 100 and 1e-4, 0.2 and 0.5, respectively. Similarly for LeNet-5, \(\gamma \) was found to be 1e-5, 2e-4 and 5e-5 for pruning ratios 0.1, 0.5 and 0.9 and 3e-5, 1e-6 and 1e-5 for sparsity ratios 0.1, 0.6 and 0.9 respectively. The results validate the bound provided in Theorem 2.

5 Conclusions

This paper has theoretically derived and experimentally validated the amount of retraining that would be required after pruning, in terms of the relative number of epochs. Also, the propagation of errors through the layers, due to pruning different layers is analysed and a bound to the amount of error that the layers contribute was derived. The parameter ‘Net Deviation’ can be used to study different pruning approaches and hence can be used as a criteria for ranking different pruning approaches. If not completely avoided, reducing the number of epochs linked to retraining the network will reduce the computational complexity involved with training a Neural Network. An empirical formula to calculate the \(\gamma \) parameter that bounds the number of epochs required for retraining, is considered as a future work.